A New Method for GNSS Multipath Mitigation with an Adaptive Frequency Domain Filter
Abstract
:1. Introduction
2. Adaptive Frequency Domain Filter Algorithm
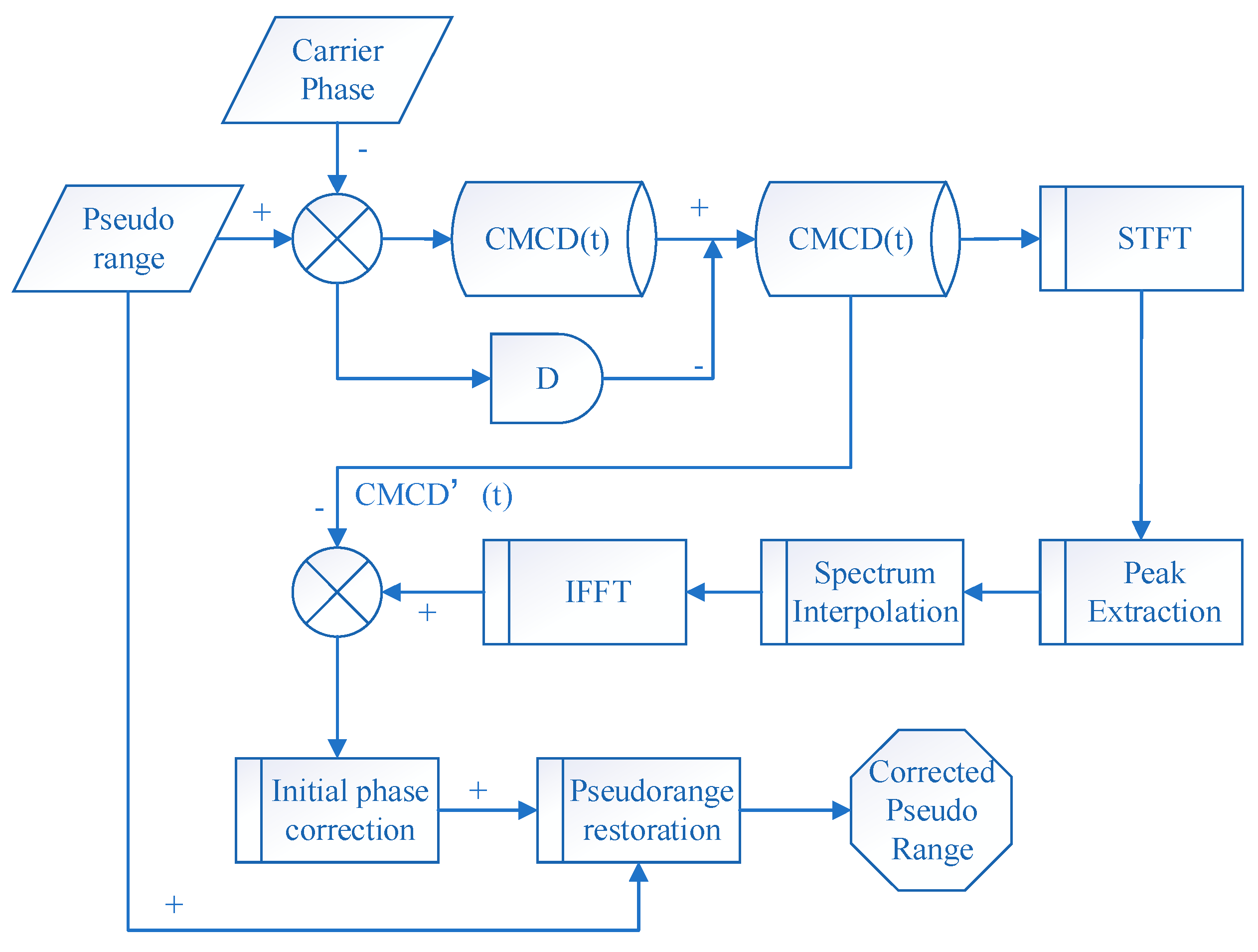
2.1. Procedure of Adaptive Frequency Domain Filter
- CMCD extraction: Using the code and carrier phase measurement as input, the CMC series can be extracted. Then, by differencing the CMC in adjacent epochs, the CMCD series can be obtained.
- STFT: With the derived CMCD, the frequency spectrum is calculated based on STFT.
- Spectrum peaks location: Using the real-time STFT frequency spectrum, the left rising slope threshold and right falling slope threshold can be obtained adaptively. Then, the positions of the spectrum peaks can be extracted.
- Spectrum interpolation: After the peak location is extracted, the peak is cut off by employing interpolation methods, which include the linear interpolation method, cubic spline interpolation, subsection Hermite interpolation method, and cubic interpolation method, etc. In this paper, the cubic interpolation method was used.
- Fourier inversion: Fourier inversion based on inverse fast Fourier transform (IFFT) is employed for the smoothed spectrum data, then the smoothed frequency-domain data is converted into time-domain data. After Fourier inversion, the corrected CMCD series can be obtained.
- Initial phase correction: Using the corrected CMCD series and former CMCD series as input, differential values of the CMCD and corrected CMCD can be obtained, and the initial phase value can be corrected afterwards.
- Pseudorange restoration: Using the differential series of CMCD and corrected CMCD, the corrected CMC series can be obtained by integration. Then, the waveform fluctuations in the pseudorange can be corrected by using the corrected CMC series and initial phase.
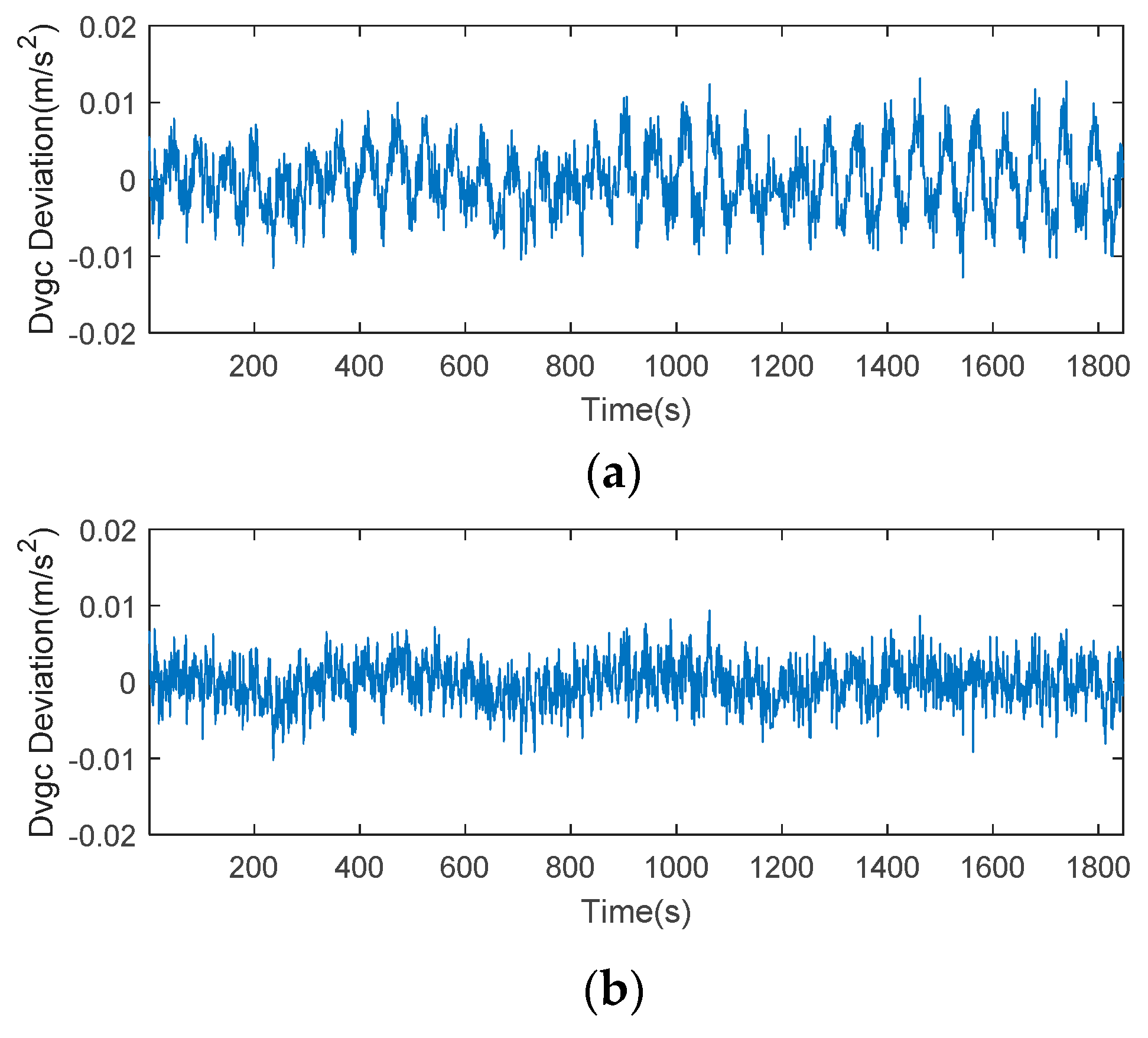
2.2. Code-Minus-Carrier Divergence
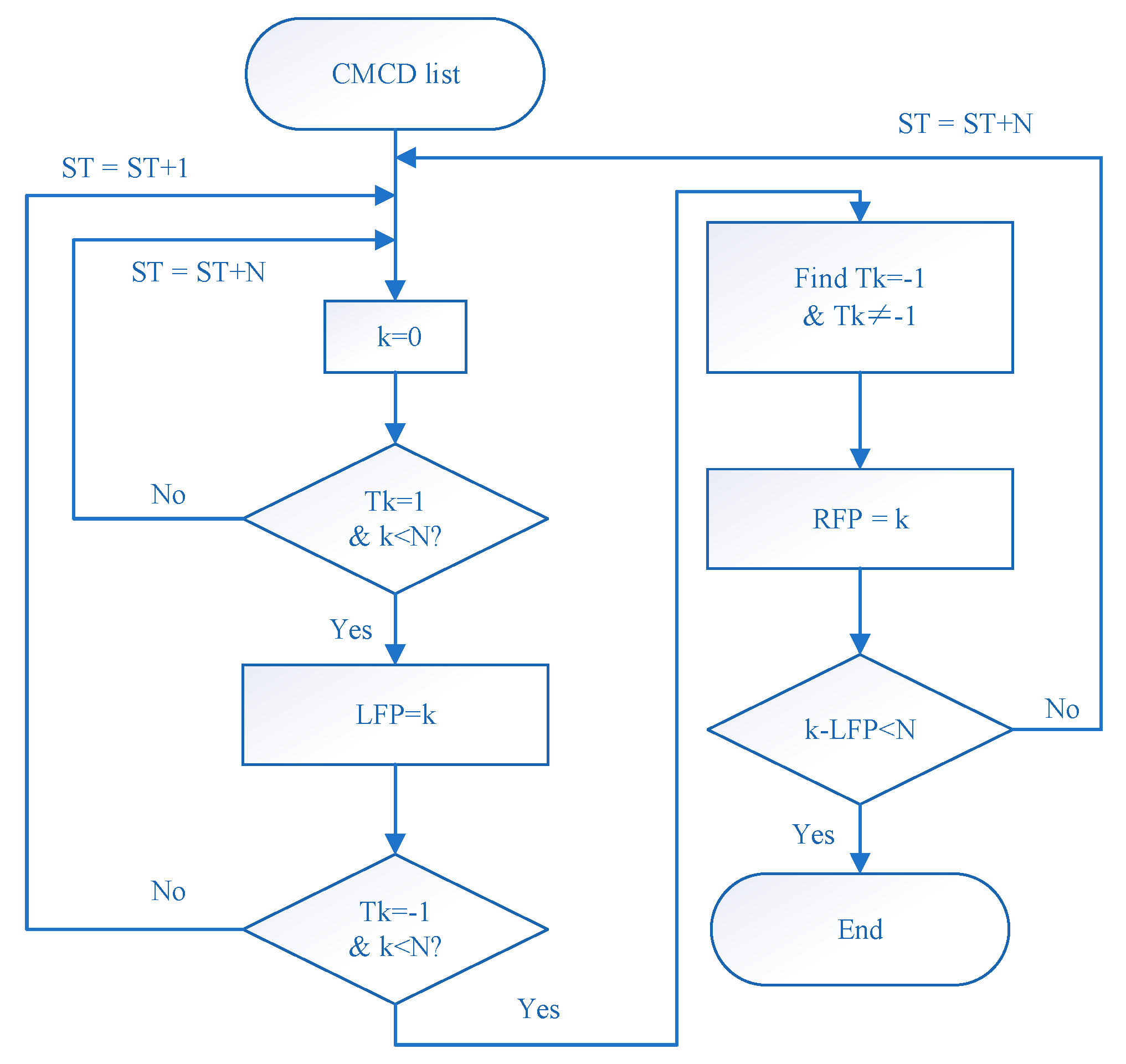
2.3. Spectrum Peak Extracting Method
- Turn the frequency spectrum calculated by STFT into a continuous spectrum. Then, the spectrum slope can be calculated. In this paper, glide window technology was used to turn the former spectrum into the continuous spectrum. Then, the significant random fluctuation could be decreased, thus the major variation tendency was kept in a continuous spectrum. The window length of glide window technology used in this experiment was 100.
- Calculate the left rising slope threshold and the right falling slope threshold. These details are presented in Section 2.4.
- Turn the continuous spectrum sequence into 0–1 series. If is greater than zero, then compare with . If is greater than , then mark the output value as 1, otherwise mark it as zero. If is less than zero, then compare with ; if is greater than , then mark it as zero, otherwise mark it as –1.
- Find out the first as the left peak point, and start counting the number of epochs. When the epoch number is less than the preset peak width , step into the next time interval if there is no . When the point is found and continuously equal to −1, set the last point equal to −1 as the right peak point. Then, the position of the frequency spectrum peak can be found. It is worth mentioning that the peak searching region should not be greater than . If epoch counting reaches without any point equal to −1 or the range between the left peak point and the right peak point is greater than , stop searching and turn to the next region.
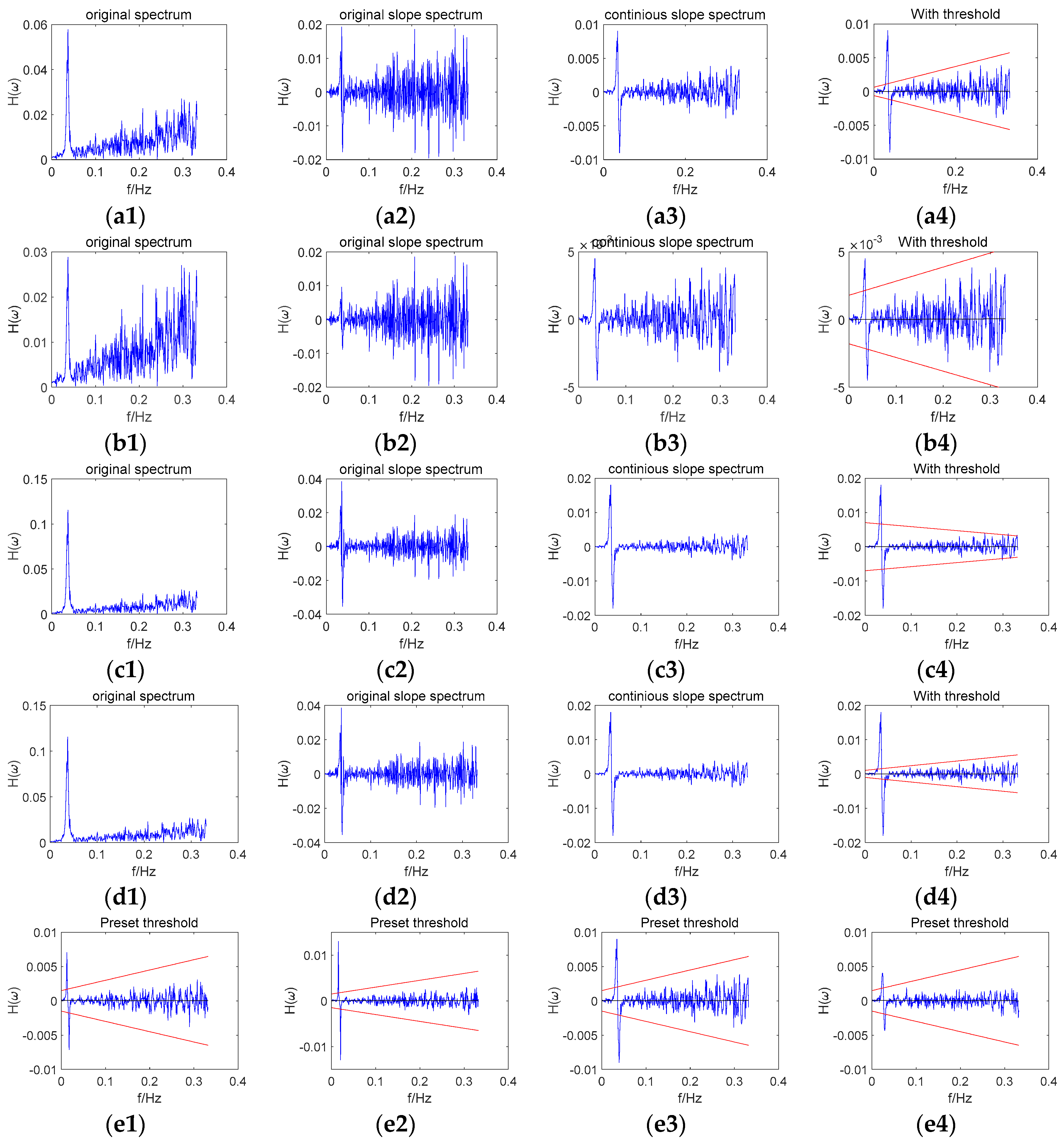
2.4. Adaptive Threshold Setting Combined Strategy
2.4.1. Adaptive Threshold Method
2.4.2. Preset Threshold Method
2.4.3. Parameter Influence in Adaptive Threshold Setting Combined Strategy
2.5. Correction Models
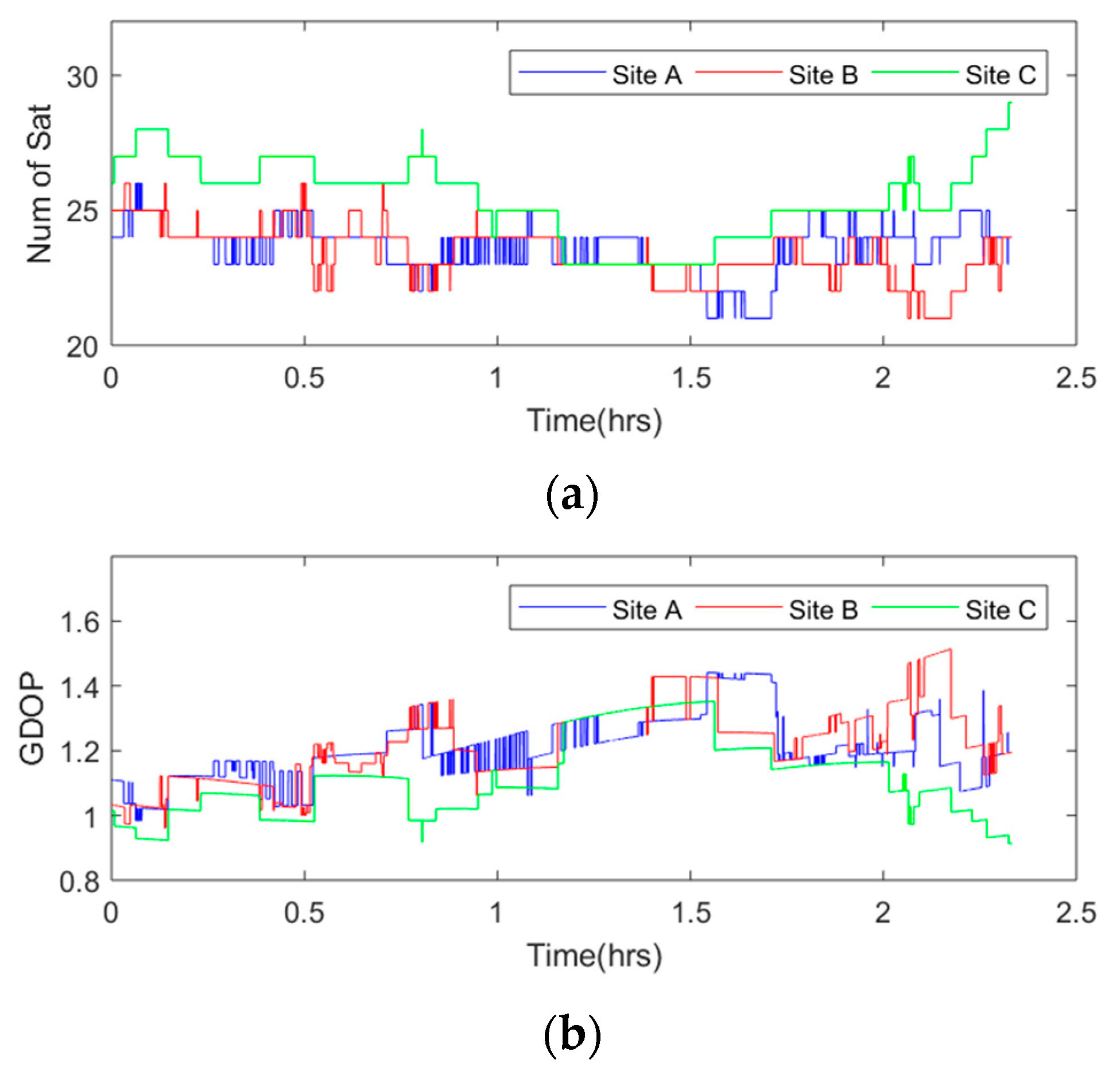
3. Datasets
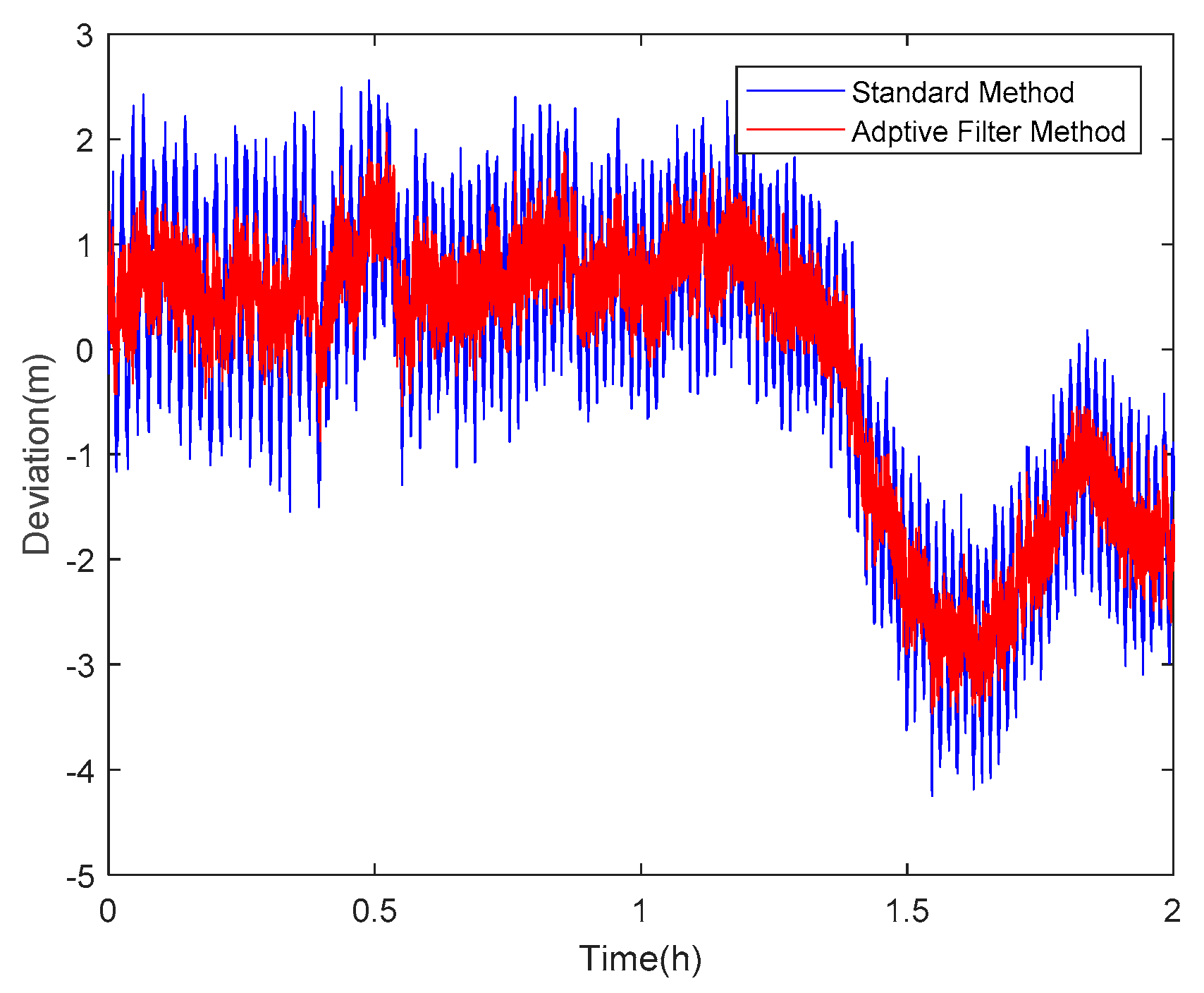
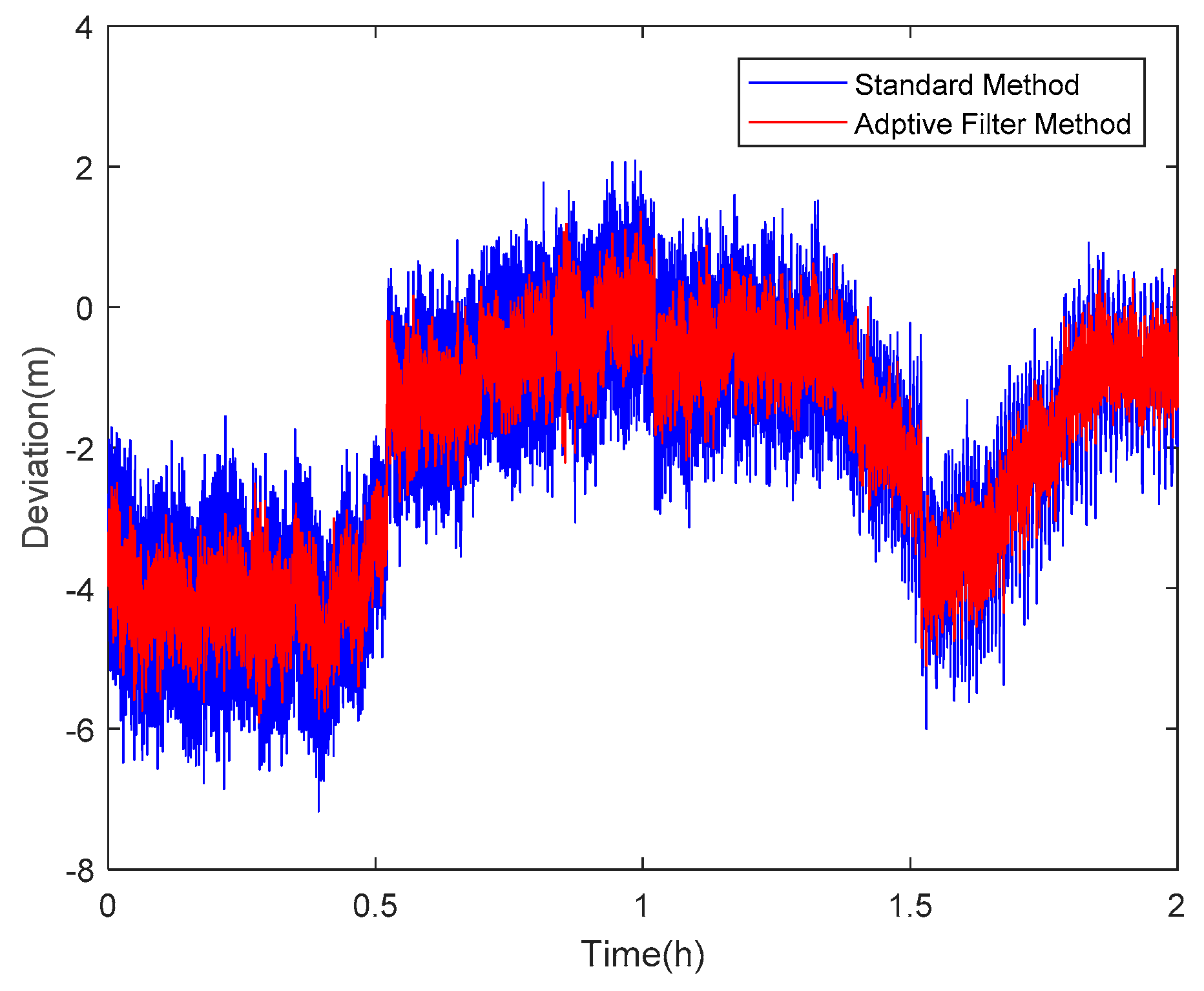
4. Results and Analysis
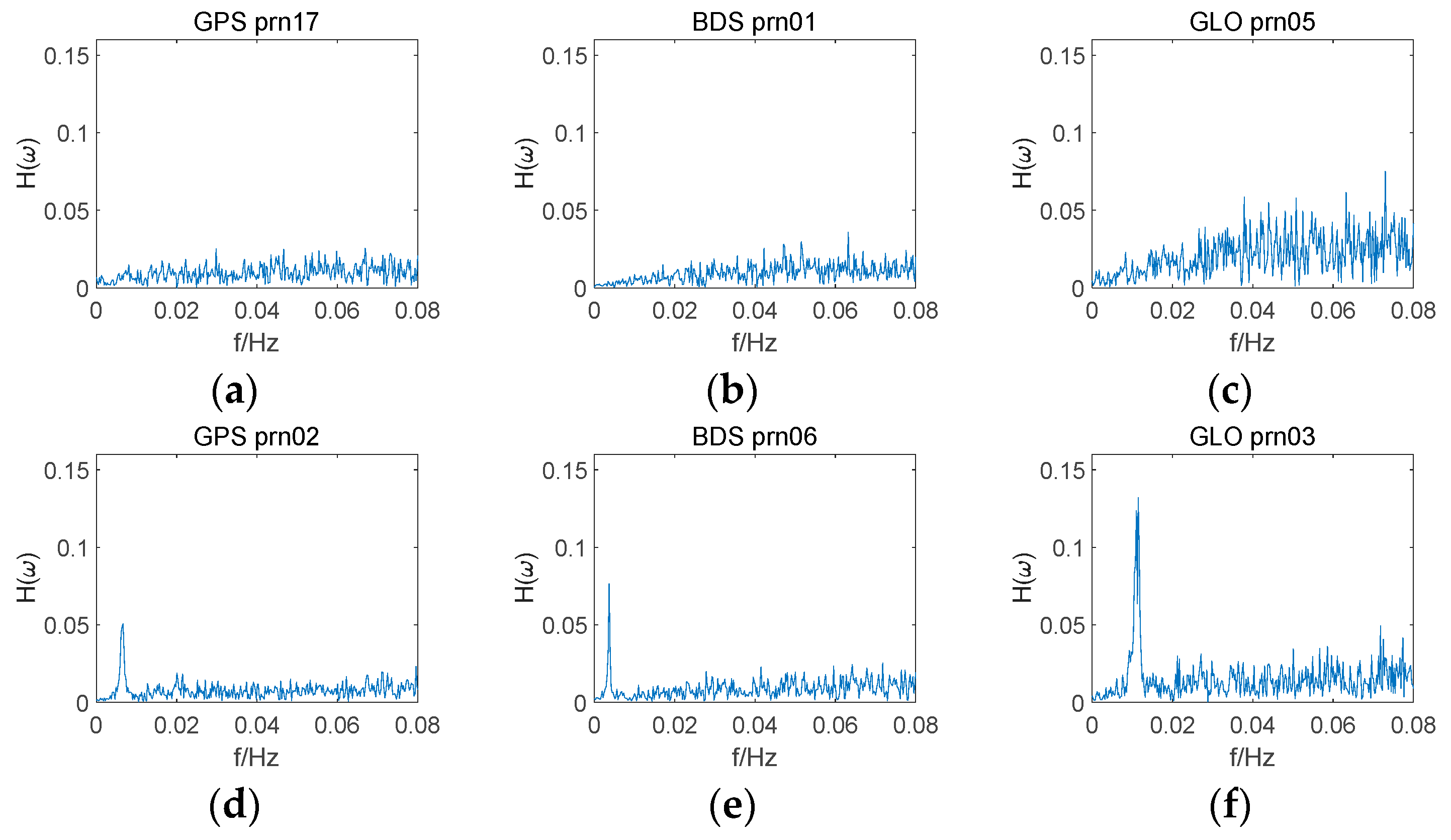
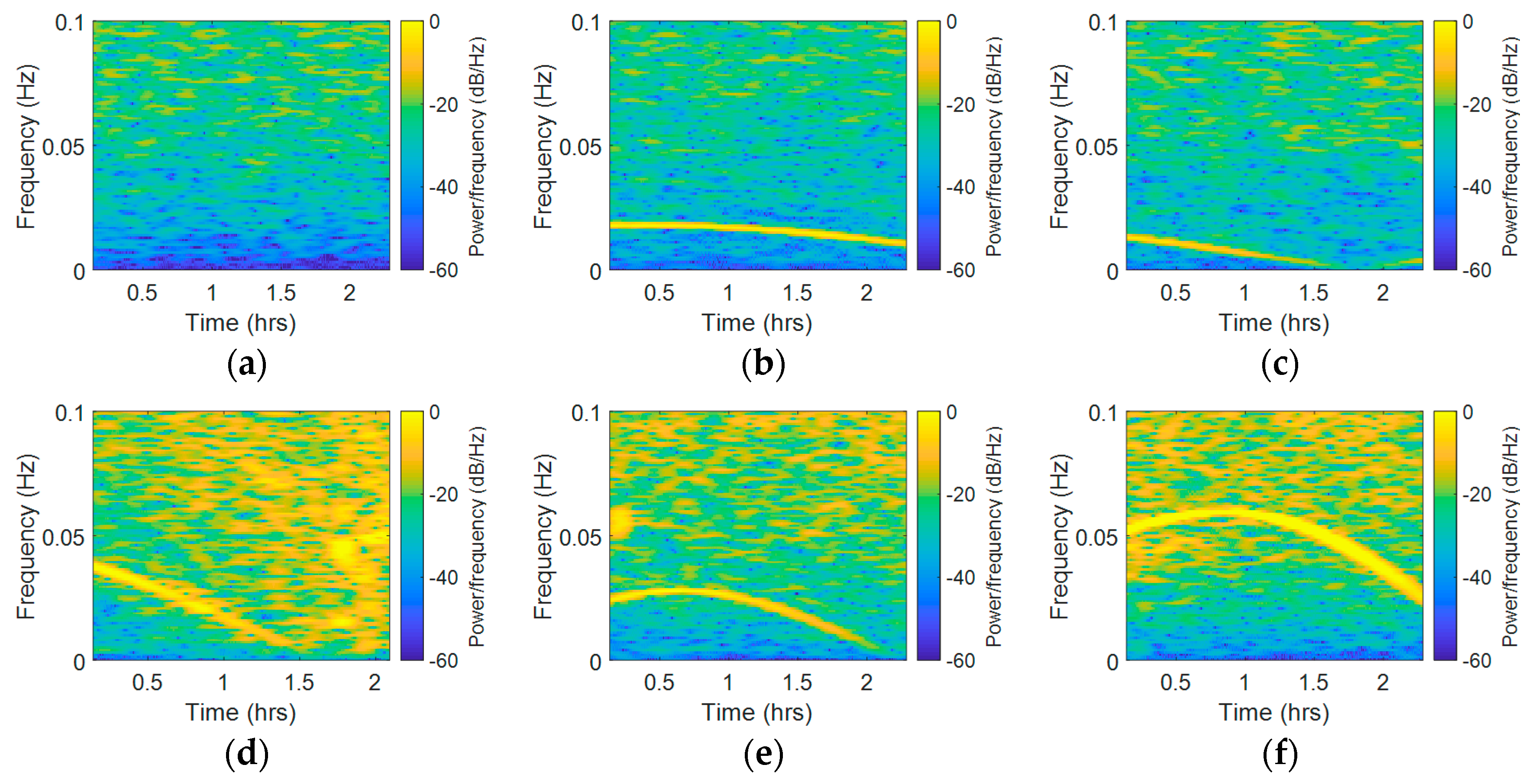
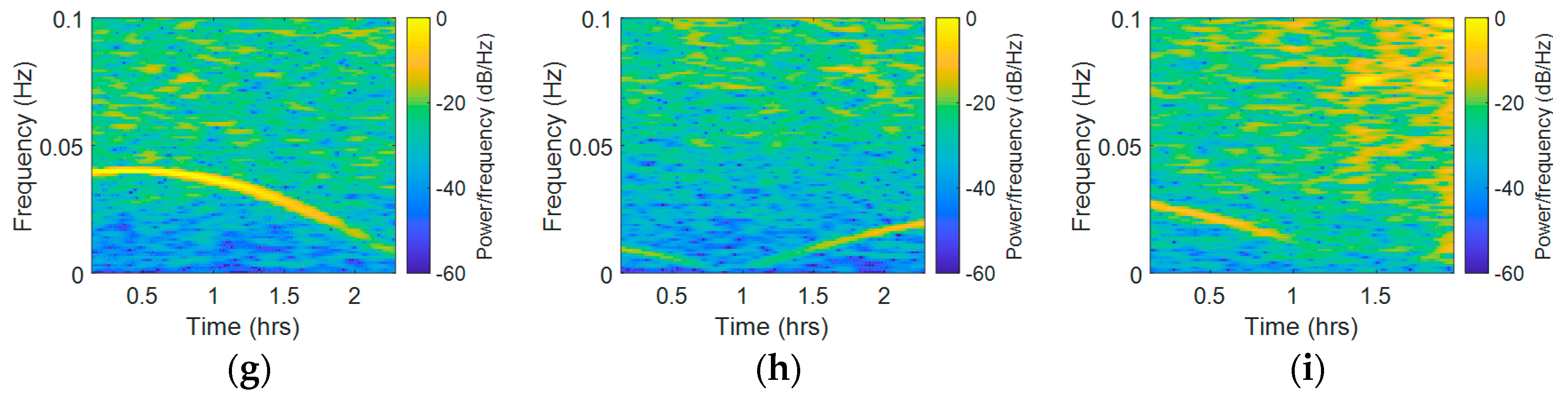
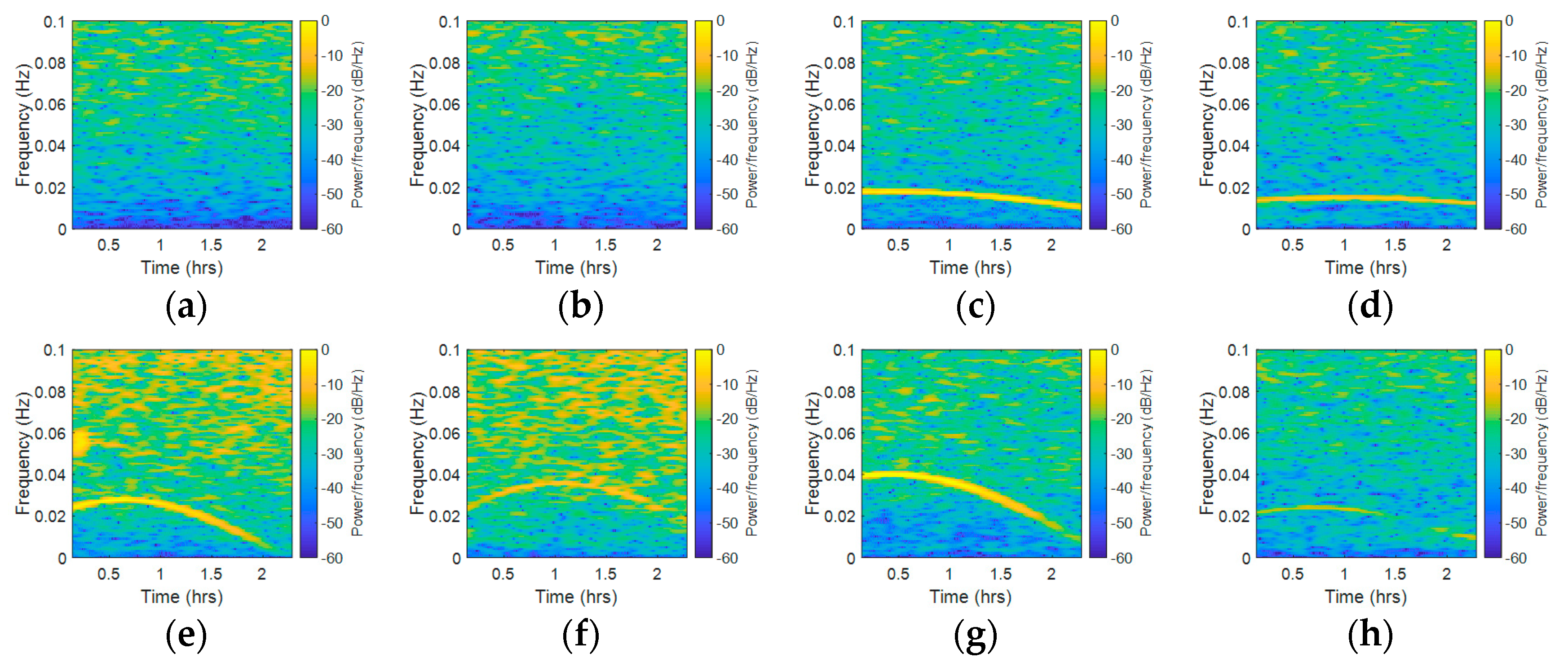
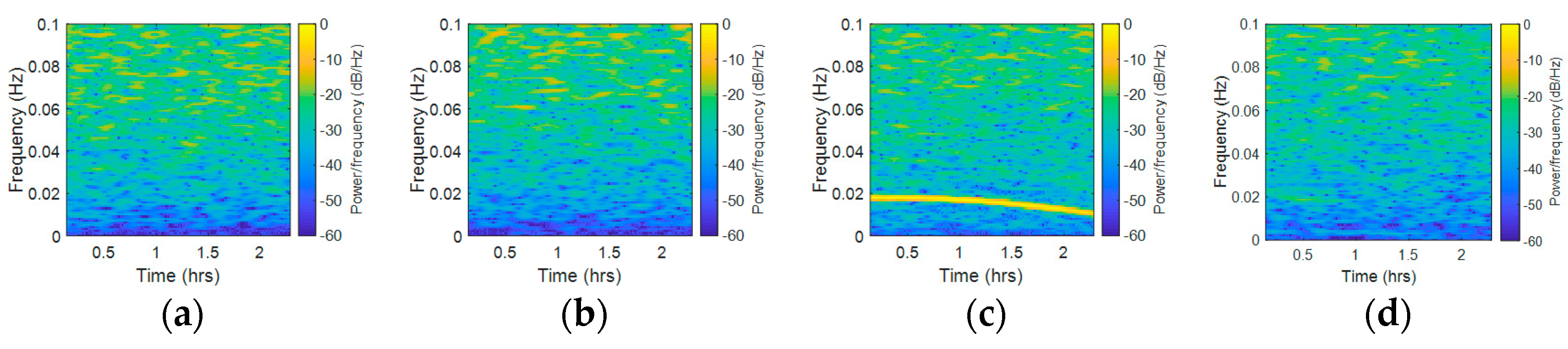
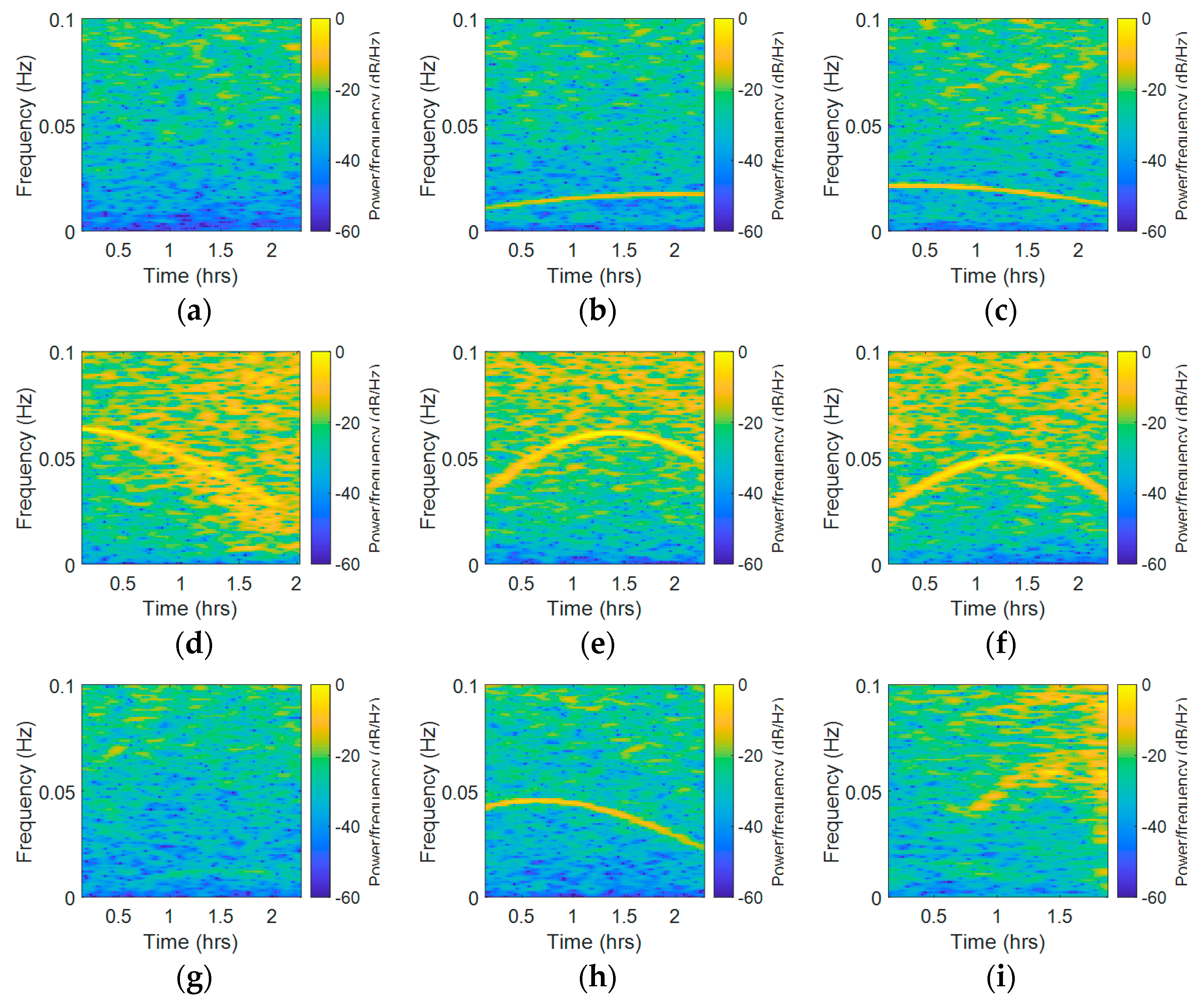
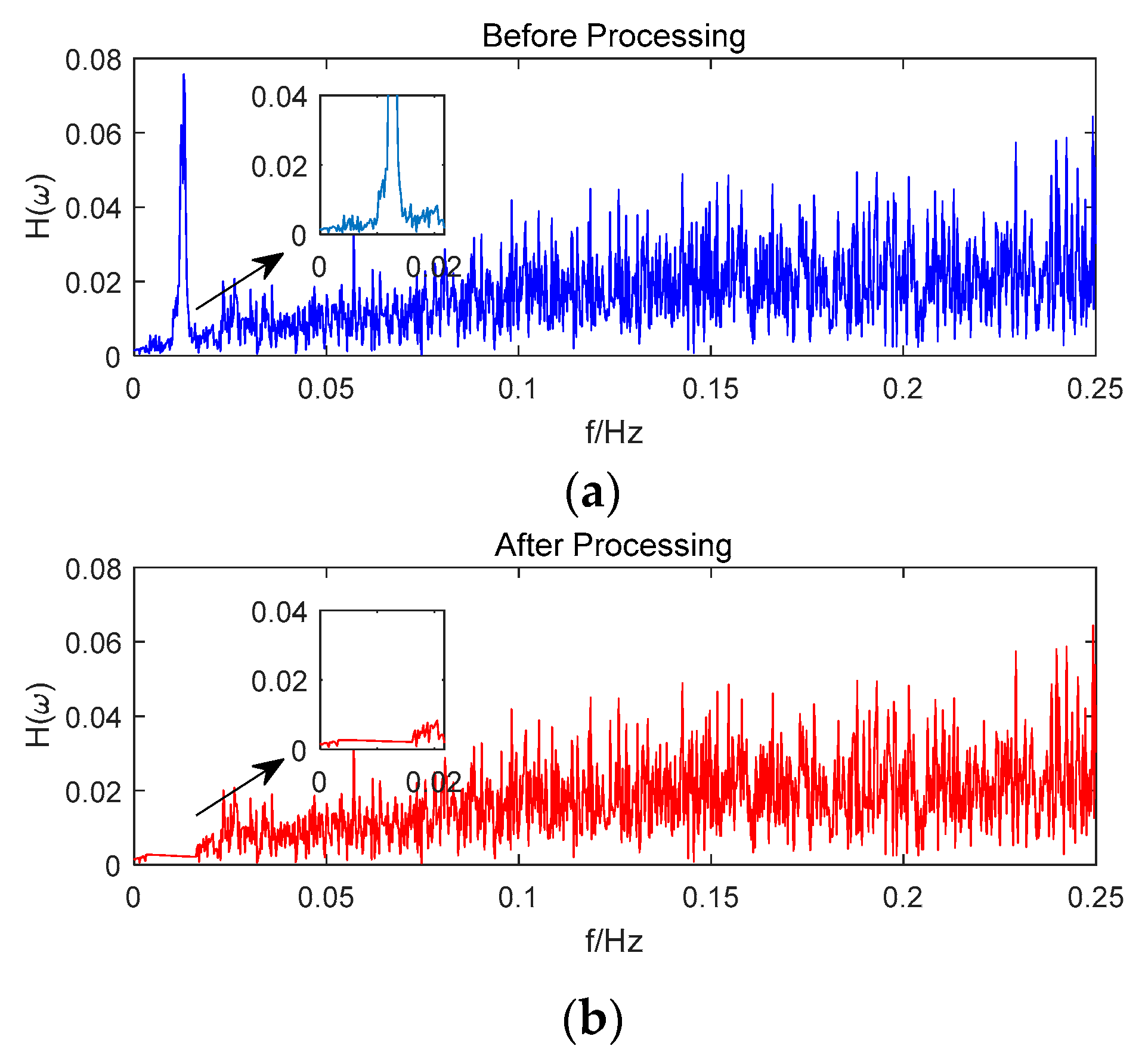
4.1. CMCD Spectral Analysis and Comparison
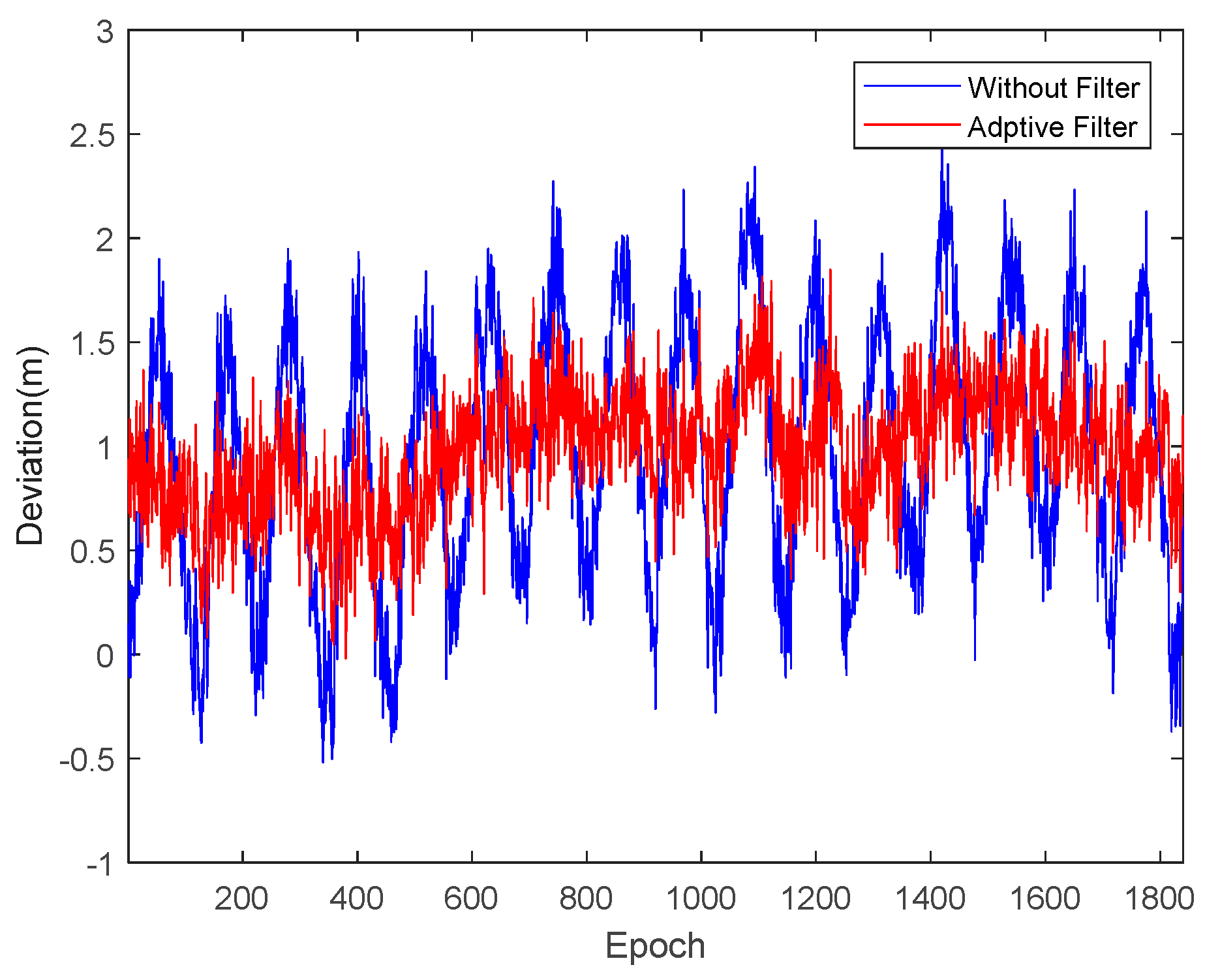
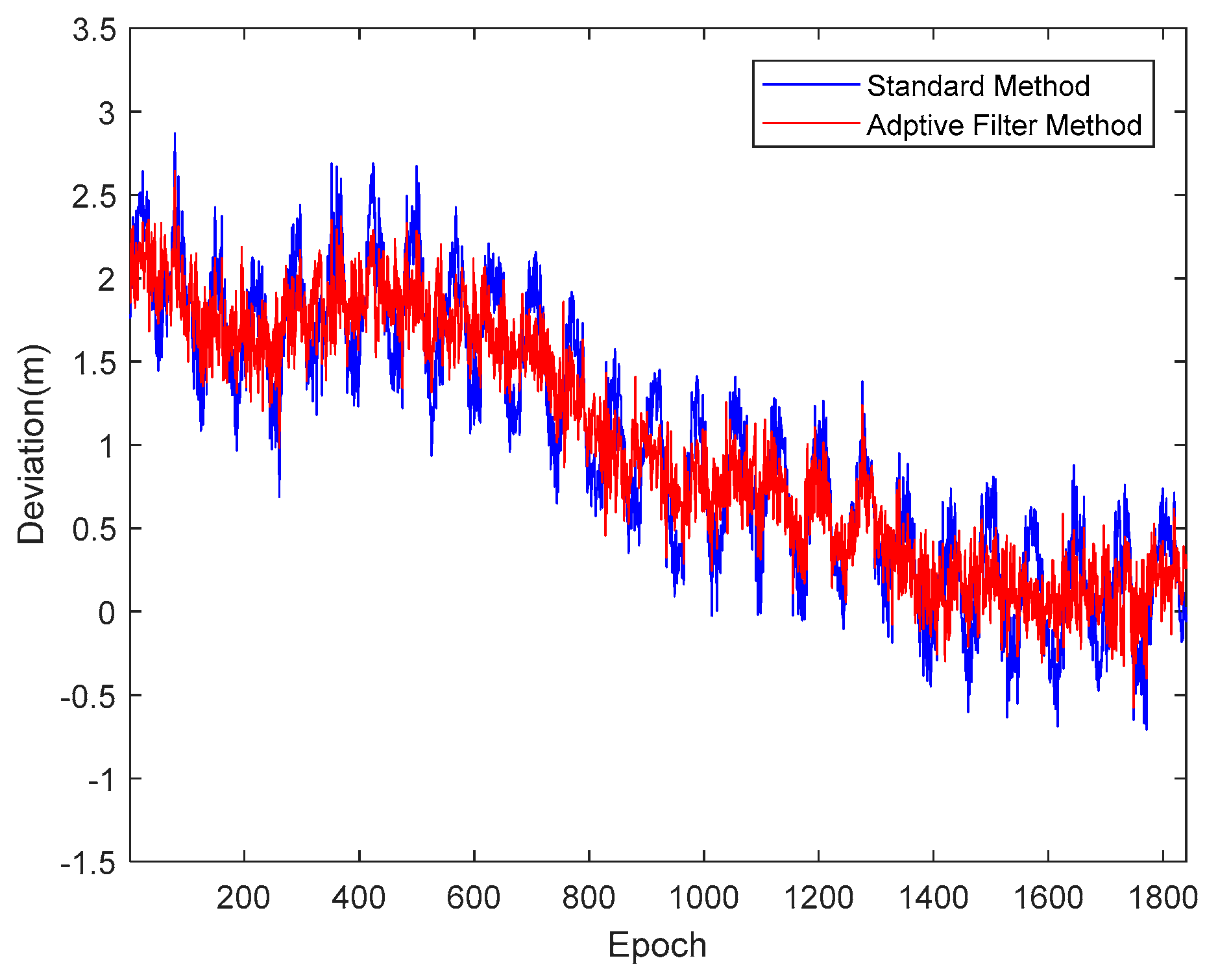
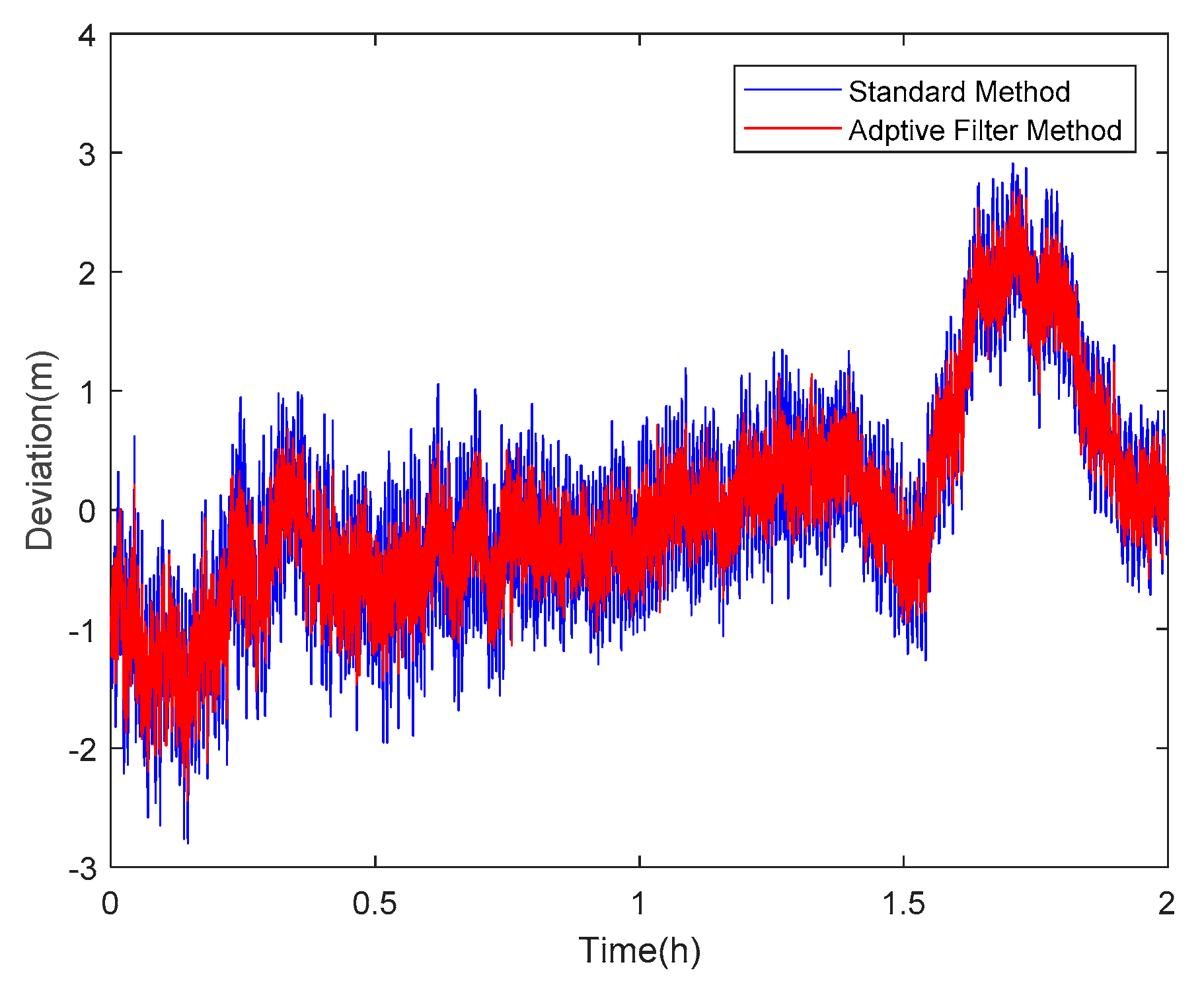
4.2. Results and Analysis of the Proposed Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hagerman, L. Effects of multipath on coherent and noncoherent PRN ranging receiver. The Aerospace Corporation Report No. TOR-0073(3020-03)-3. 1973. [Google Scholar]
- Spiker, J.J. GPS signal structure and performance characteristics. Navigation 1978, 25, 121–146. [Google Scholar] [CrossRef]
- Ye, S.; Chen, D.; Liu, Y.; Jiang, P.; Tang, W.; Xia, P. Carrier phase multipath mitigation for beidou navigation satellite system. GPS Solut. 2015, 19, 545–557. [Google Scholar] [CrossRef]
- Wang, D.; Meng, X.; Gao, C.; Pan, S.; Chen, Q. Multipath extraction and mitigation for bridge deformation monitoring using a single-difference model. Adv. Space Res. 2017, 60, 2882–2895. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Z.; Tan, C.; Si, L.; Zhang, L.; Liu, X. Adaptive wavelet threshold denoising method for machinery sound based on improved fruit fly optimization algorithm. Appl. Sci. 2016, 6, 199. [Google Scholar] [CrossRef]
- Chen, D.; Ye, S.; Xia, J.; Liu, Y.; Xia, P. A geometry-free and ionosphere-free multipath mitigation method for bds three-frequency ambiguity resolution. J. Geod. 2016, 90, 703–714. [Google Scholar] [CrossRef]
- Lau, L. Wavelet Packets Based Denoising Method for Measurement Domain Repeat-Time Multipath Filtering in GPS Static High-Precision Positioning; Springer: New York, NY, USA, 2017. [Google Scholar]
- Ray, J.K.; Cannon, M.E.; Fenton, P.C. Mitigation of static carrier-phase multipath effects using multiple closely spaced antennas. Navigation 1999, 46, 193–201. [Google Scholar] [CrossRef]
- Zhang, K.; Li, B.; Zhu, X.; Chen, H.; Sun, G. Multipath detection based on single orthogonal dual linear polarized GNSS antenna. GPS Solut. 2017, 21, 1–9. [Google Scholar] [CrossRef]
- Young, L.E.; Meehan, T.K.; Spitzmesser, D.J.; Tranquilla, J.T. GPS antenna selection: Preliminary range and field test results. In Proceedings of the 1988 Antenna Technology and Applied Electromagnetics, Winnipeg, MB, Canada, 10–12 August 1988. [Google Scholar]
- Tranquilla, J.M.; Carr, J.P.; Al-Rizzo, H.M. Analysis of a choke ring ground plane for multipath control in global positioning system (GPS) applications. IEEE Trans. Antennas Propag. 1994, 42, 905–911. [Google Scholar] [CrossRef]
- Kesler, J.; Haykin, S. A new adaptive antenna for elevation angle estimation in the presence of multipath. Antennas Propag. Soc. Int. Symp. 2003, 130, 303–308. [Google Scholar]
- Fenton, P.; Ford, T.; Dierendonck, A.J.V. Novatel’s GPS receiver: The high performance OEM sensor of the future. In Proceedings of the 4th International Technical Meeting of the Satellite Division of the Institute of Navigation, Albuquerque, NM, USA, 11–13 September 1991; pp. 49–58. [Google Scholar]
- Dierendonck, A.J.V.; Fenton, P.; Ford, T. Theory and performance of narrow correlator spacing in a GPS receiver. Navigation 1992, 39, 265–283. [Google Scholar] [CrossRef]
- Townsend, B.R.; Fenton, P.C. A practical approach to the reduction of pseudorange multipath errors in a L1 GPS receiver. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, Salt Lake City, UT, USA, 20–23 September 1994; pp. 143–148. [Google Scholar]
- Lippincott Wendy, M.T. Method for calculating multipath environment and impact on GPS receiver solution accuracy. Multimed. Tools Appl. 1996, 57, 633–650. [Google Scholar]
- Zhong, P.; Ding, X.; Yuan, L.; Xu, Y.; Kwok, K.; Chen, Y. Sidereal filtering based on single differences for mitigating GPS multipath effects on short baselines. J. Geod. 2010, 84, 145–158. [Google Scholar] [CrossRef]
- Barton, P.; Waddoup, W.D. Reduction of tracking errors induced by multipath at low elevation angles. In Proceedings of the Numerical Transmission by Cable, Houston, TX, USA, 30 November–4 December 1980; Volume 1. [Google Scholar]
- Pozo-Ruz, A.; Martinez, J.L.; Garcia-Cerezo, A. New satellite selection criterion for DGPS using two low-cost receivers. In Proceedings of the IEEE International Conference on Robotics and Automation, Belgium, Belgium, 20 May 1998; Volume 3, pp. 1883–1888. [Google Scholar]
- Mat Amin, Z.; Wan Akib, W.A.; Twigg, D.R. The Time Series Analysis in GPS Structural Monitoring Schemes. Map Asia. Bangkok, Thailand, 2002. Available online: https://core.ac.uk/download/pdf/11780868.pdf (accessed on 23 January 2018).
- Wang, J.; Li, Z.K.; Wang, Z.J. Study on low-pass filter based GPS/INS integrated navigation model. J. Navig. Position. 2013, 1, 22–27. [Google Scholar]
- Simili, D.V.; Pervan, B. Code-Carrier Divergence Monitoring for the GPS Local Area Augmentation System. In Proceedings of the 2006 IEEE/ION Position, Location, and Navigation Symposium, Coronado, CA, USA, 25–27 April 2006; pp. 483–493. [Google Scholar]
- Ge, L.; Han, S.; Rizos, C. Multipath mitigation of continuous GPS measurements using an adaptive filter. GPS Solut. 2000, 4, 19–30. [Google Scholar] [CrossRef]
- Azarbad, M.R.; Mosavi, M.R. A new method to mitigate multipath error in single-frequency GPS receiver with wavelet transform. GPS Solut. 2014, 18, 189–198. [Google Scholar] [CrossRef]
- Mcgraw, G. Generalized divergence-free carrier smoothing with applications to dual frequency differential GPS. Navigation 2009, 56, 115–122. [Google Scholar] [CrossRef]
- Zhang, Y.; Bartone, C. Multipath mitigation in the frequency domain. In Proceedings of the Position Location and Navigation Symposium, Monterey, CA, USA, 26–29 April 2004; pp. 486–495. [Google Scholar]
- Bartone, C.; Zhang, Y. Real-Time Code Multipath Mitigation in the Frequency Domain Using FDsmooth™ for Global Navigation Satellite Systems. U.S. Patent No. 20050216210A1, 29 September 2005. [Google Scholar]
- Kim, E.; Walter, T.; Powell, J.D. Adaptive carrier smoothing using code and carrier divergence. In Proceedings of the National Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 22–24 January 2007. [Google Scholar]
- Griffin, D.; Lim, J.S. Signal estimation from modified short-time fourier transform. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 236–243. [Google Scholar] [CrossRef]
- Fourier, J.B. The Analytical Theory of Heat; Translated by Alexander Freeman, Translated from French; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Yalvac, S.; Ustun, A.; Berber, M.M. Detecting and removing repetitive errors from PPP time series by means of adaptive filter. In Proceedings of the 2017 Signal Processing Symposium, Jachranka, Poland, 12–14 September 2017; pp. 1–5. [Google Scholar]
- Yang, J.; Ma, J.; Liu, X.; Qi, L.; Wang, Z.; Zhuang, Y.; Shi, L. A height constrained adaptive kalman filtering based on climbing motion model for GNSS positioning. IEEE Sens. J. 2017, 17, 7105–7113. [Google Scholar] [CrossRef]
- Ugazio, S.; Presti, L.L. Effects of colored noise in Linear Adaptive Filters applied to GNSS multipath detection. In Proceedings of the Design and Architectures for Signal and Image Processing, Cagliari, Italy, 8–10 October 2016; pp. 126–133. [Google Scholar]
- Cheng, L.; Wang, Z.Y.; Xie, G.; Yan, G.W. A sliding average Extended Kalman Filter and its application in multipath estimation. In Proceedings of the IEEE International Conference on Control and Automation, Kathmandu, Nepal, 1–3 June 2016; pp. 944–946. [Google Scholar]
- Park, B.; Sohn, K.; Kee, C. Optimal hatch filter with an adaptive smoothing window width. J. Navig. 2008, 61, 435–454. [Google Scholar] [CrossRef]
- Hatch, R. The synergism of GPS code and carrier measurements. In Proceedings of the International Geodetic Symposium on Satellite Doppler Positioning, Las Cruces, NM, USA, 8–12 February 1982; pp. 1213–1231. [Google Scholar]
- Haykin, S. Adaptive Filter Theory, 2nd ed.; Auflage: Berlin, Germany, 2002; Volume 4, p. 469. [Google Scholar]
- Xie, G. Optimal On-Airport Monitoring of the Integrity of GPS-Based Landing Systems. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2004. [Google Scholar]
- Bracewell, R.N. The Fourier Transform and Its Applications, 3rd ed.; McGraw-Hill: Boston, MA, USA, 2000; ISBN 0-07-116043-4. [Google Scholar]
- Pinsky, M.A. Introduction to Fourier Analysis and Wavelets; Brooks/Cole: Pacific Grove, CA, USA, 2002; ISBN 0-534-37660-6. [Google Scholar]
- Bailey, D.H.; Swarztrauber, P.N. A fast method for the numerical evaluation of continuous Fourier and Laplace transforms. SIAM J. Sci. Comput. 1994, 15, 1105–1110. [Google Scholar] [CrossRef]

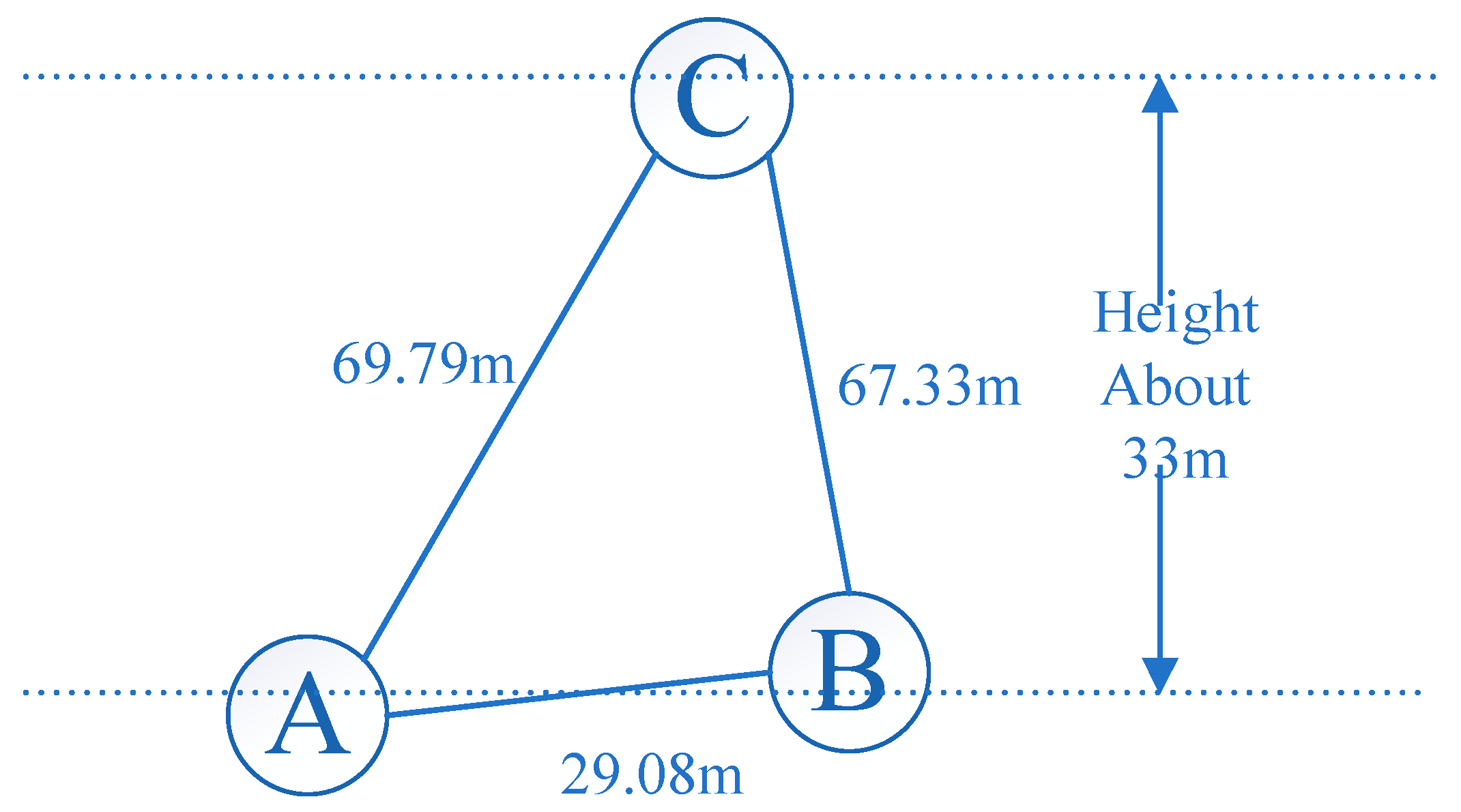









| Dataset 1 | Dataset 2 | Dataset 3 | Dataset 4 | |
|---|---|---|---|---|
| Station | A | B | C | A |
| Receiver | Trimble R9 | Trimble R9 | Trimble R9 | Trimble R9 |
| Antenna | Choke ring | Choke ring | Choke ring | Choke ring |
| Sampling Interval/s | 0.5 | 0.5 | 0.5 | 0.5 |
| Cut-off angle/° | 5 | 5 | 5 | 5 |
| Systems | G/C/R | G/C/R | G/C/R | G/C/R |
| Baseline/m | 0 | 29.08 | 69.79 | 0 |
| Observation date | 19 October | 19 October | 19 October | 27 October |
| Time/hour | 2.5 | 2.5 | 2.5 | 2.5 |
| Environment | Partial occlusion | Partial occlusion | Open environment | Partial occlusion |
| System | Prn | Without Filter | Proposed Method (m) | Improvement Percentage (%) |
|---|---|---|---|---|
| BDS | 01 | 0.2510 | 0.2507 | 0.1 |
| BDS | 02 | 0.3272 | 0.3264 | 0.2 |
| BDS | 03 | 0.2765 | 0.2763 | 0.08 |
| BDS | 04 | 0.2876 | 0.2873 | 0.1 |
| BDS | 05 | 0.3685 | 0.3684 | 0.05 |
| BDS | 06 | 0.6714 | 0.2562 | 61.84 |
| BDS | 08 | 0.7636 | 0.6060 | 20.64 |
| BDS | 09 | 0.6651 | 0.3182 | 52.16 |
| BDS | 13 | 0.5050 | 0.2817 | 44.22 |
| GLO | 04 | 1.0315 | 0.8321 | 19.34 |
| GLO | 05 | 0.6747 | 0.5780 | 14.34 |
| GLO | 18 | 0.6074 | 0.4613 | 24.05 |
| GLO | 19 | 0.8938 | 0.4404 | 50.73 |
| GLO | 20 | 0.9260 | 0.7013 | 20.23 |
| GPS | 02 | 0.4392 | 0.2713 | 38.22 |
| GPS | 05 | 0.3474 | 0.2777 | 20.07 |
| GPS | 06 | 0.4215 | 0.3102 | 26.41 |
| GPS | 13 | 0.3993 | 0.2359 | 40.90 |
| GPS | 25 | 0.5735 | 0.4643 | 19.05 |
| GPS | 29 | 0.4333 | 0.2844 | 34.37 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Guo, F.; Zhang, X.; Liu, W.; Li, X.; Wu, R. A New Method for GNSS Multipath Mitigation with an Adaptive Frequency Domain Filter. Sensors 2018, 18, 2514. https://doi.org/10.3390/s18082514
Yu S, Guo F, Zhang X, Liu W, Li X, Wu R. A New Method for GNSS Multipath Mitigation with an Adaptive Frequency Domain Filter. Sensors. 2018; 18(8):2514. https://doi.org/10.3390/s18082514
Chicago/Turabian StyleYu, Siqi, Fei Guo, Xiaohong Zhang, Wanke Liu, Xin Li, and Renpan Wu. 2018. "A New Method for GNSS Multipath Mitigation with an Adaptive Frequency Domain Filter" Sensors 18, no. 8: 2514. https://doi.org/10.3390/s18082514
APA StyleYu, S., Guo, F., Zhang, X., Liu, W., Li, X., & Wu, R. (2018). A New Method for GNSS Multipath Mitigation with an Adaptive Frequency Domain Filter. Sensors, 18(8), 2514. https://doi.org/10.3390/s18082514




