Generalized Optical Design of the Double-Row Circular Multi-Pass Cell
Abstract
:1. Introduction
2. Analytical Tracing of Circular Multi-Pass Cell
2.1. Traditional Circular Multi-Pass Cell
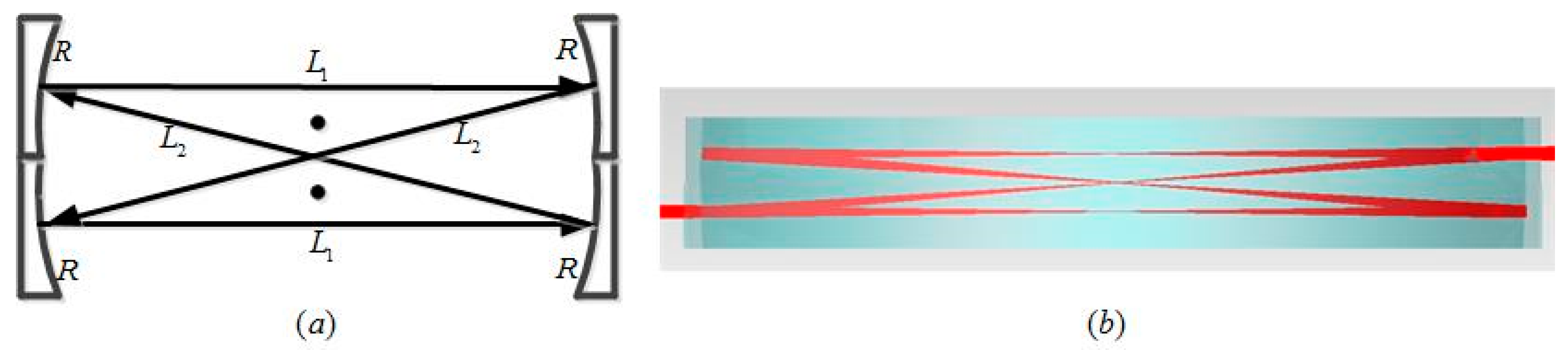
2.2. Double-Row Circular Multi-Pass Cell
3. Parametric Design
3.1. Incident Angle θ
3.2. Stability Analysis: Upper Limit of c
3.3. Projection of Angle between Incident and Exit
4. Simulation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- White, J.U. Long Optical Paths of Large Aperture. J. Opt. Soc. Am. 1942, 32, 285–288. [Google Scholar] [CrossRef]
- Herriott, D.; Kogelnik, H.; Kompfner, R. Off-axis paths in spherical mirror interferometers. Appl. Opt. 1964, 3, 523–526. [Google Scholar] [CrossRef]
- Bernstein, H.J.; Herzberg, G. Rotation-vibration spectra of diatomic and simple polyatomic molecules with long absorbing paths. I. the spectrum of fluoroform (chf3) from 2.4 μ to 0.7 μ. J. Chem. Phys. 1948, 16, 30–39. [Google Scholar] [CrossRef]
- Pickett, H.M.; Bradley, G.M.; Strauss, H.L. A new white type multiple pass absorption cell. Appl. Opt. 1970, 9, 2397–2398. [Google Scholar] [CrossRef] [PubMed]
- Chernin, S.M.; Barskaya, E.G. Optical multipass matrix systems. Appl. Opt. 1991, 30, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Chernin, S. Development of optical multipass matrix systems. Opt. Acta Int. J. Opt. 2001, 48, 619–632. [Google Scholar] [CrossRef]
- Chernin, S. Promising version of the three-objective multipass matrix system. Opt. Express 2002, 10, 104–107. [Google Scholar] [CrossRef] [PubMed]
- Glowacki, D.R.; Goddard, A.; Seakins, P.W. Design and performance of a throughput-matched, zero-geometric-loss, modified three objective multipass matrix system for FTIR spectrometry. Appl. Opt. 2007, 46, 7872–7883. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Sun, L.; Yang, Z.; Liu, Z. Generalized design of a zero-geometric-loss, astigmatism-free, modified four-objective multipass matrix system. Appl. Opt. 2016, 55, 1435–1443. [Google Scholar] [CrossRef] [PubMed]
- Tuzson, B.; Mangold, M.; Looser, H.; Manninen, A.; Emmenegger, L. Compact multipass optical cell for laser spectroscopy. Opt. Lett. 2013, 38, 257–259. [Google Scholar] [CrossRef] [PubMed]
- Herriott, D.R.; Schulte, H.J. Folded Optical Delay Lines. Appl. Opt. 1965, 4, 883–889. [Google Scholar] [CrossRef]
- McManus, J.B.; Kebabian, P.L.; Zahniser, M.S. Astigmatic mirror multipass absorption cells for long-path-length spectroscopy. Appl. Opt. 1995, 34, 3336–3348. [Google Scholar] [CrossRef] [PubMed]
- Chernin, A.S.M. Multipass systems of new generation in high-resolution spectroscopy for fundamental and applied atmosphere investigations. Opt. Instrum. Gas Emiss. Monit. Atmos. Meas. 1995, 2366, 408–418. [Google Scholar]
- Chernin, S.M. New generation of multipass systems in high resolution spectroscopy. Spectrochim. Acta A 1996, 52, 1009–1022. [Google Scholar] [CrossRef]
- Ofner, J.; Krüger, H.U.; Zetzsch, C. Circular multireflection cell for optical spectroscopy. Appl. Opt. 2010, 49, 5001–5004. [Google Scholar] [CrossRef] [PubMed]
- Riedel, J.; Yan, S.; Kawamata, H.; Liu, K. A simple yet effective multipass reflector for vibrational excitation in molecular beams. Rev. Sci. Instrum. 2008, 79, 033105. [Google Scholar] [CrossRef] [PubMed]
- Bernacki, B.E. Multipass Optical Device and Process for Gas and Analyte Determination. U.S. Patent 7876443, 25 January 2011. [Google Scholar]
- Manninen, A.; Tuzson, B.; Looser, H.; Bonetti, Y.; Emmenegger, L. Versatile multipass cell for laser spectroscopic trace gas analysis. Appl. Phys. B 2012, 109, 461–466. [Google Scholar] [CrossRef]
- Jouy, P.; Mangold, M.; Tuzson, B.; Emmenegger, L.; Chang, Y.C.; Hvozdara, L.; Herzig, H.P.; Wägli, P.; Homsy, A.; de Rooij, N.F.; et al. Mid-infrared spectroscopy for gases and liquids based on quantum cascade technologies. Analyst 2014, 139, 2039–2046. [Google Scholar] [CrossRef] [PubMed]
- Markus, M.; Tuzson, B.; Hundt, M.; Jágerská, J.; Looser, H.; Emmenegger, L. Circular paraboloid reflection cell for laser spectroscopic trace gas analysis. J. Opt. Soc. Am. A 2016, 33, 913–919. [Google Scholar]
- Graf, M.; Looser, H.; Emmenegger, L.; Tuzson, B. Beam folding analysis and optimization of mask-enhanced toroidal multipass cells. Opt. Lett. 2017, 42, 3137–3140. [Google Scholar] [CrossRef] [PubMed]
- Svelto, O.; Hanna, D.C. Principles of Lasers, 4th ed.; Plenum Press: New York, NY, USA, 1998; pp. 169–173. [Google Scholar]
- Chen, K.; Yang, H.; Sun, L.; Jin, G. Generalized method for calculating astigmatism of the unit-magnification multipass system. Appl. Opt. 2010, 49, 1964–1971. [Google Scholar] [CrossRef] [PubMed]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Guo, Y.; Ming, X.; Sun, L. Generalized Optical Design of the Double-Row Circular Multi-Pass Cell. Sensors 2018, 18, 2680. https://doi.org/10.3390/s18082680
Yang Z, Guo Y, Ming X, Sun L. Generalized Optical Design of the Double-Row Circular Multi-Pass Cell. Sensors. 2018; 18(8):2680. https://doi.org/10.3390/s18082680
Chicago/Turabian StyleYang, Zheng, Yin Guo, Xianshun Ming, and Liqun Sun. 2018. "Generalized Optical Design of the Double-Row Circular Multi-Pass Cell" Sensors 18, no. 8: 2680. https://doi.org/10.3390/s18082680
APA StyleYang, Z., Guo, Y., Ming, X., & Sun, L. (2018). Generalized Optical Design of the Double-Row Circular Multi-Pass Cell. Sensors, 18(8), 2680. https://doi.org/10.3390/s18082680




