Improving High-Throughput Phenotyping Using Fusion of Close-Range Hyperspectral Camera and Low-Cost Depth Sensor
Abstract
:1. Introduction
1.1. Previous Work
Close-Range Hyperspectral Camera
1.2. Combination of Hyperspectral Images and 3D Point Clouds
2. Materials and Methods
2.1. Physical Equipments
2.1.1. Hyperspectral Sensing System
2.1.2. Low-Cost Depth Sensor
2.1.3. Reference Gauge
2.1.4. Imaging Station
2.2. Plant Materials
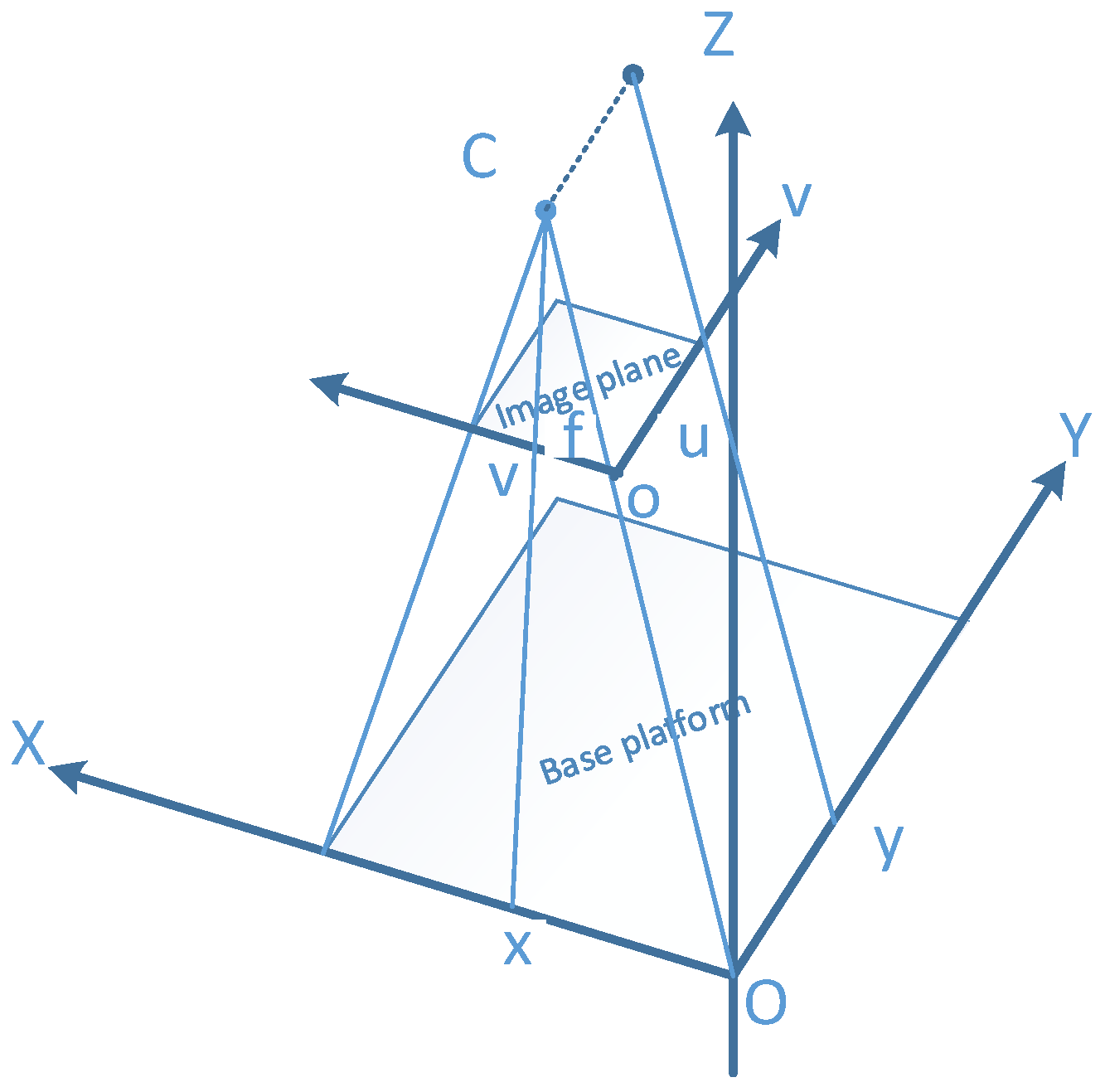
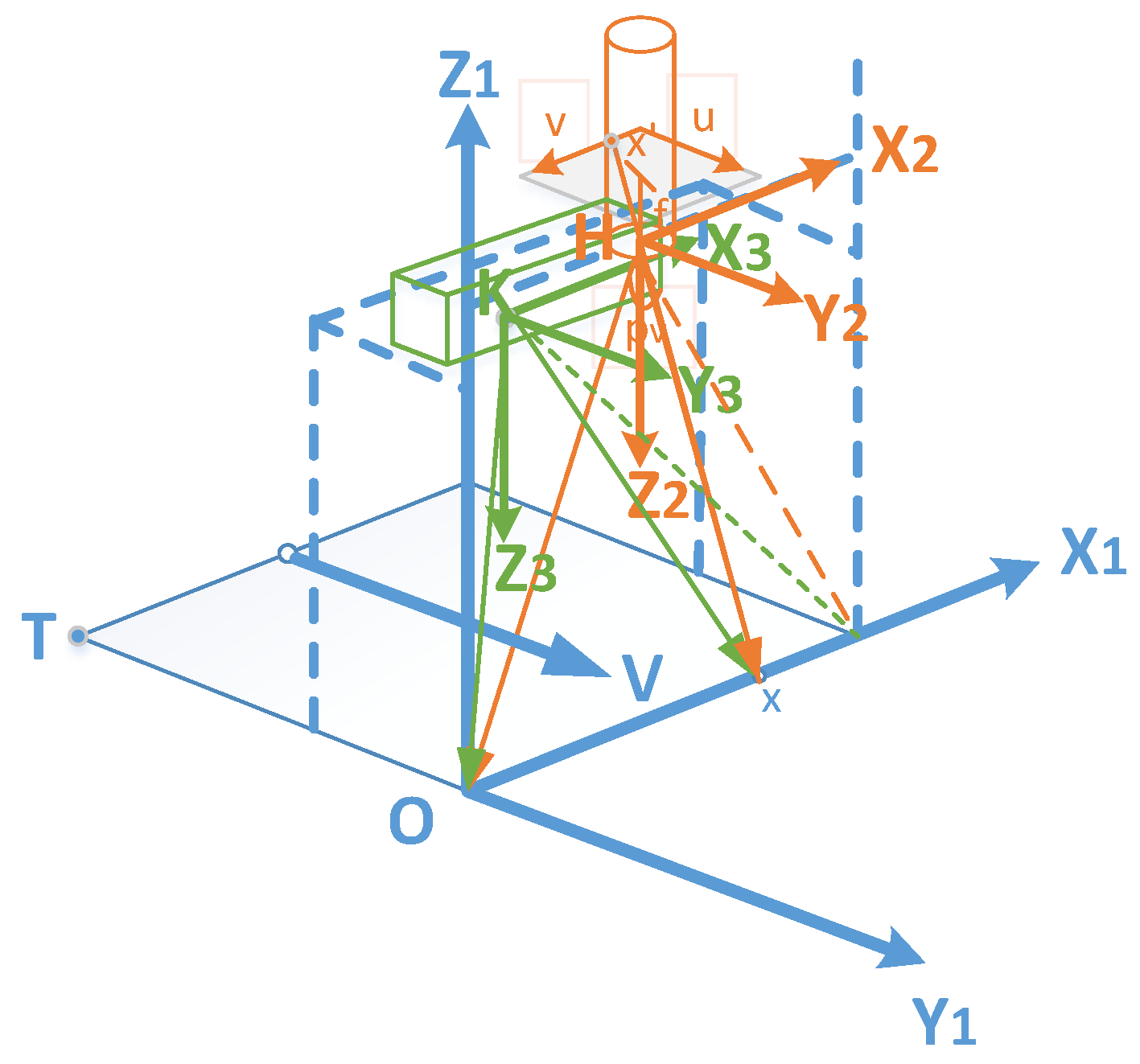
2.3. Fusion of a Close-Range Hyperspectral Camera and a Depth Sensor
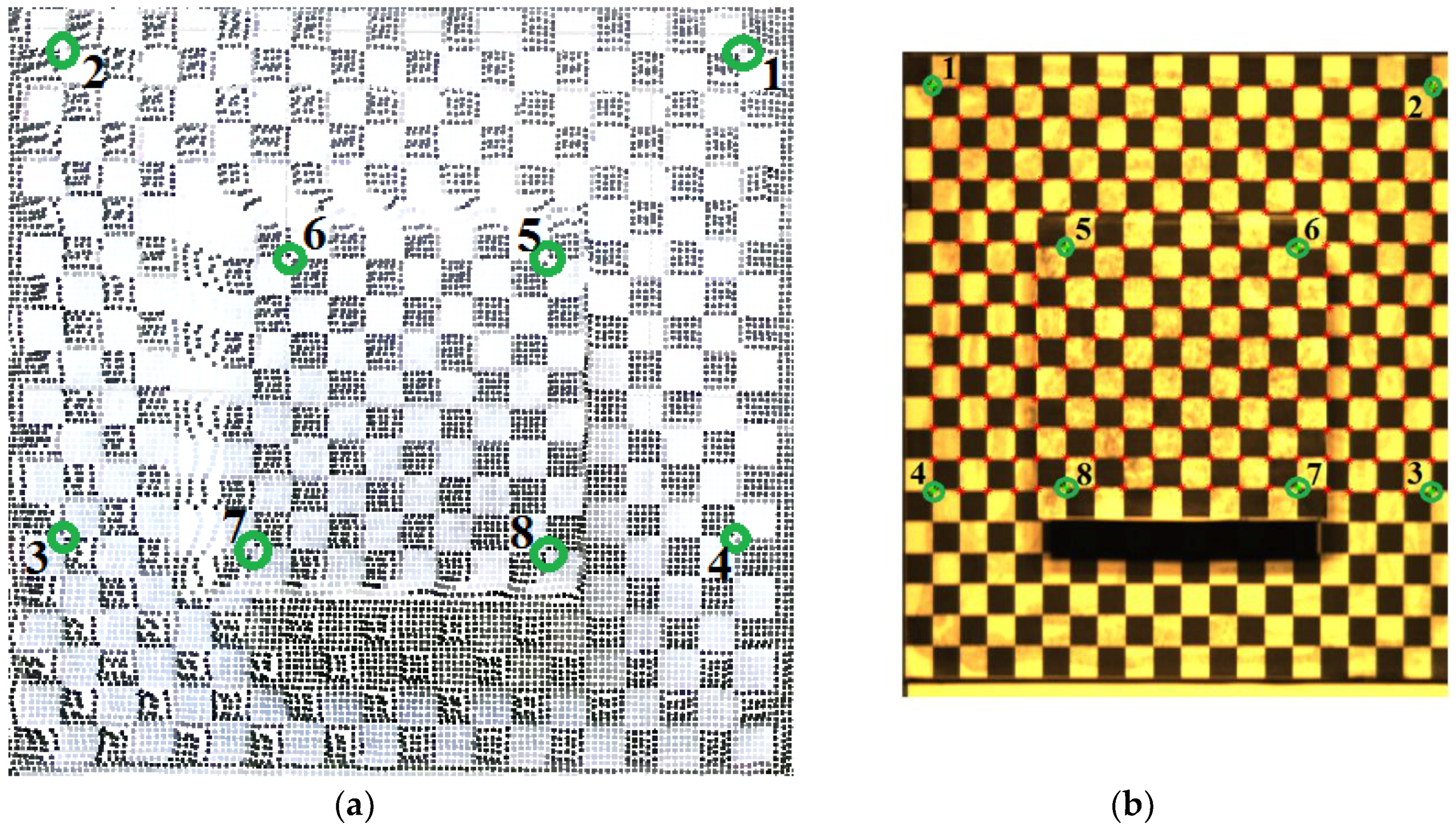
2.3.1. Semi-Automatic Coordinate Measurement
2.3.2. Alignment of Depth and Hyperspectral Sensor
3. Results & Discussion
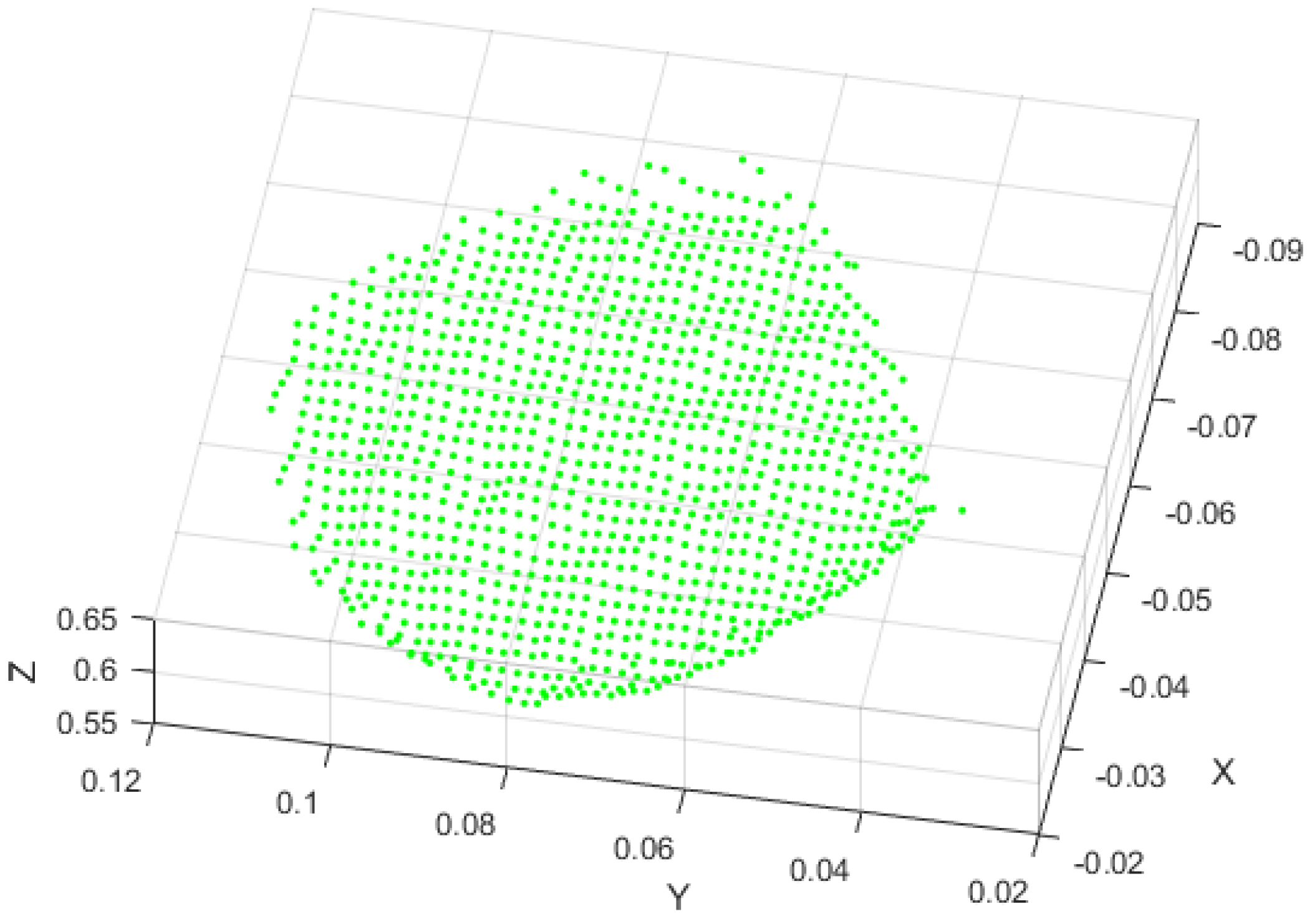
3.1. Fusion Model Experiments
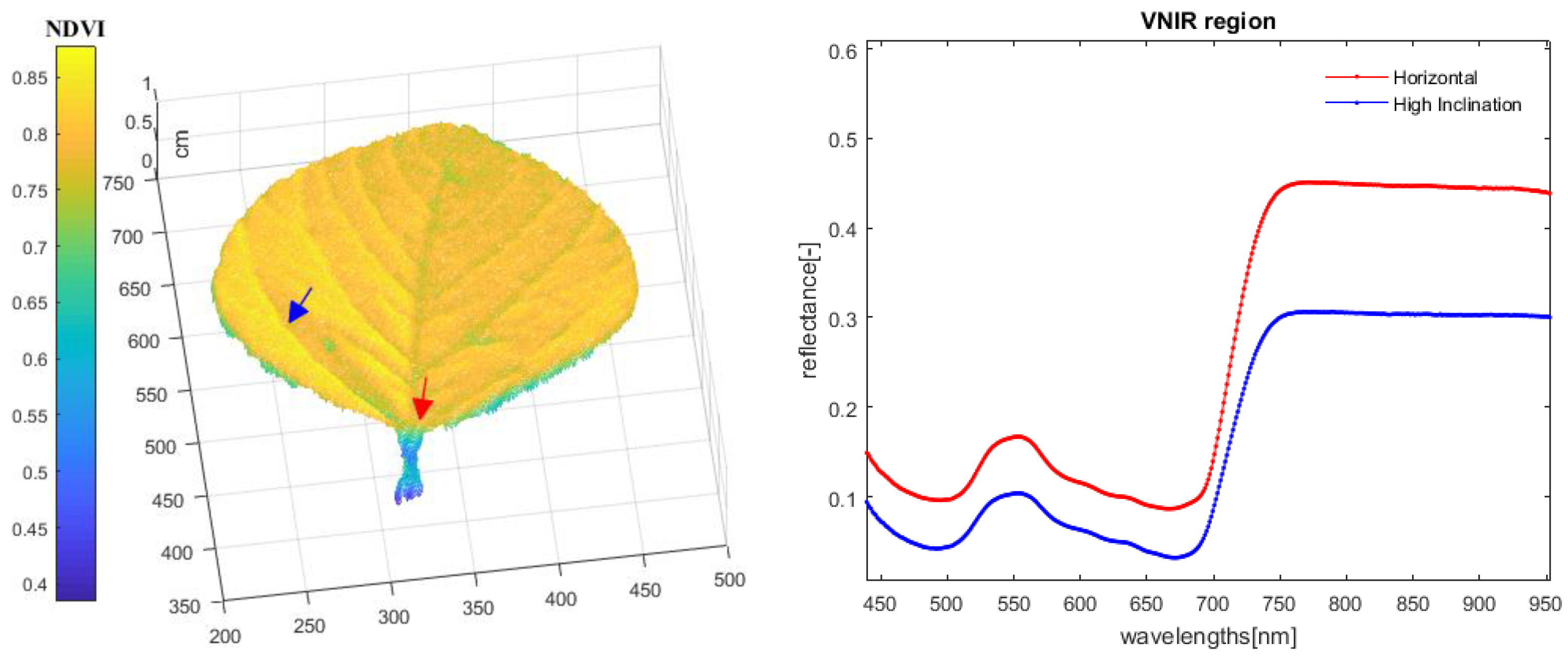
3.2. Validation Experiments
3.3. Result Summary
3.4. Prospects of Fusion Model for Plant High-Throughput Phenotyping
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bai, G.; Ge, Y.; Hussain, W.; Baenziger, P.S.; Graef, G. A multi-sensor system for high throughput field phenotyping in soybean and wheat breeding. Comput. Electron. Agric. 2016, 128, 181–192. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q.; Huang, D. A review of imaging techniques for plant phenotyping. Sensors 2014, 14, 20078–20111. [Google Scholar] [CrossRef] [PubMed]
- Thenkabail, P.S.; Lyon, J.G.; Huete, A. Advances in Hyperspectral Remote Sensing of Vegetation and Agricultural Croplands. In Hyperspectral Remote Sensing of Vegetation; CRC Press: Boca Raton, FL, USA, 2012; pp. 3–32. ISBN 978-1-4398-4538-7. [Google Scholar]
- Gonzalezdugo, V.; Hernandez, P.; Solis, I.; Zarcotejada, P. Using high-resolution hyperspectral and thermal airborne imagery to assess physiological condition in the context of wheat phenotyping. Remote Sens. 2015, 7, 13586–13605. [Google Scholar] [CrossRef]
- Thomas, S.; Kuska, M.T.; Bohnenkamp, D.; Brugger, A.; Alisaac, E.; Wahabzada, M. Benefits of hyperspectral imaging for plant disease detection and plant protection: A technical perspective. J. Plant Dis. Prot. 2018, 125, 5–20. [Google Scholar] [CrossRef]
- Sytar, O.; Brestic, M.; Zivcak, M.; Olsovska, K.; Kovar, M.; Shao, H. Applying hyperspectral imaging to explore natural plant diversity towards improving salt stress tolerance. Sci. Total Environ. 2016, 578, 90. [Google Scholar] [CrossRef] [PubMed]
- De Jong, S.M.; Addink, E.A.; Hoogenboom, P.; Nijland, W. The spectral response of Buxus sempervirens to different types of environmental stress—A laboratory experiment. ISPRS J. Photogramm. Remote Sens. 2012, 74, 56–65. [Google Scholar] [CrossRef]
- Mahlein, A.-K.; Oerke, E.-C.; Steiner, U.; Dehne, H.-W. Recent advances in sensing plant diseases for precision crop protection. Eur. J. Plant Pathol. 2012, 133, 197–209. [Google Scholar] [CrossRef]
- Sun, L.; Simmons, B.A.; Singh, S. Understanding tissue specific compositions of bioenergy feedstocks through hyperspectral Raman imaging. Biotechnol. Bioeng. 2011, 108, 286–295. [Google Scholar] [CrossRef] [PubMed]
- Furbank, R.T.; Tester, M. Phenomics–technologies to relieve the phenotyping bottleneck. Trends Plant Sci. 2011, 16, 635–644. [Google Scholar] [CrossRef] [PubMed]
- Behmann, J.; Mahlein, A.K.; Paulus, S.; Dupuis, J.; Kuhlmann, H.; Oerke, E.C.; Plümer, L. Generation and application of hyperspectral 3D plant models: methods and challenges. Mach. Vis. Appl. 2016, 27, 611–624. [Google Scholar] [CrossRef]
- Féret, J.B.; Gitelson, A.A.; Noble, S D.; Jacquemoud, S. PROSPECT-D: Towards modeling leaf optical properties through a complete lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef] [Green Version]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; Ustin, S.L. PROSPECT+ SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Jay, S.; Bendoula, R.; Hadoux, X.; Féret, J.B.; Gorretta, N. A physically-based model for retrieving foliar biochemistry and leaf orientation using close-range imaging spectroscopy. Remote Sens. Environ. 2016, 177, 220–236. [Google Scholar] [CrossRef]
- Wilson, R.T. Py6S: A Python interface to the 6S radiative transfer model. Comput. Geosci. 2013, 51, 166–171. [Google Scholar] [CrossRef] [Green Version]
- Behmann, J.; Mahlein, A.K.; Paulus, S.; Kuhlmann, H.; Oerke, E.C.; Plümer, L. Calibration of hyperspectral close-range pushbroom cameras for plant phenotyping. ISPRS J. Photogramm. Remote Sens. 2015, 106, 172–182. [Google Scholar] [CrossRef]
- Kornus, W.; Lehner, M.; Schroeder, M. Geometric in-flight calibration of the stereoscopic line-CCD scanner MOMS-2P. ISPRS J. Photogramm. Remote Sens. 2000, 55, 59–71. [Google Scholar] [CrossRef]
- Poli, D.; Toutin, T. Review of developments in geometric modelling for high resolution satellite pushbroom sensors. Photogramm. Rec. 2012, 27, 58–73. [Google Scholar] [CrossRef]
- Špiclin, Ž.; Katrašnik, J.; Bürmen, M.; Pernuš, F.; Likar, B. Geometric calibration of a hyperspectral imaging system. Appl. Opt. 2010, 49, 2813–2818. [Google Scholar] [CrossRef]
- Lawrence, K.C.; Park, B.; Windham, W.R.; Mao, C. Calibration of a pushbroom hyperspectral imaging system for agricultural inspection. Trans. ASAE 2003, 46, 513. [Google Scholar] [CrossRef]
- Gupta, R.; Hartley, R.I. Linear pushbroom cameras. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 963–975. [Google Scholar] [CrossRef] [Green Version]
- Wagner, B.; Santini, S.; Ingensand, H.; Gärtner, H. A tool to model 3D coarse-root development with annual resolution. Plant Soil 2011, 346, 79–96. [Google Scholar] [CrossRef]
- Hosoi, F.; Nakabayashi, K.; Omasa, K. 3-D modeling of tomato canopies using a high-resolution portable scanning lidar for extracting structural information. Sensors 2011, 11, 2166–2174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Omasa, K.; Hosoi, F.; Konishi, A. 3D lidar imaging for detecting and understanding plant responses and canopy structure. J. Exp. Bot. 2006, 58, 881–898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biskup, B.; Scharr, H.; Schurr, U.; Rascher, U.W.E. A stereo imaging system for measuring structural parameters of plant canopies. Plant Cell Environ. 2007, 30, 1299–1308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tilly, N.; Hoffmeister, D.; Liang, H.; Cao, Q.; Liu, Y.; Lenz-Wiedemann, V.; Bareth, G. Evaluation of terrestrial laser scanning for rice growth monitoring. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, b7. [Google Scholar] [CrossRef]
- Bellasio, C.; Olejníčková, J.; Tesař, R.; Šebela, D.; Nedbal, L. Computer reconstruction of plant growth and chlorophyll fluorescence emission in three spatial dimensions. Sensors 2012, 12, 1052–1071. [Google Scholar] [CrossRef] [PubMed]
- Paulus, S.; Schumann, H.; Kuhlmann, H.; Léon, J. High-precision laser scanning system for capturing 3D plant architecture and analysing growth of cereal plants. Biosyst. Eng. 2014, 121, 1–11. [Google Scholar] [CrossRef]
- Liang, J.; Zia, A.; Zhou, J.; Sirault, X. 3D plant modelling via hyperspectral imaging. In Proceedings of the 2013 IEEE International Conference on Computer Vision Workshops (ICCVW), Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Bareth, G.; Aasen, H.; Bendig, J.; Gnyp, M.L.; Bolten, A.; Jung, A.; Soukkamäki, J. Low-weight and UAV-based hyperspectral full-frame cameras for monitoring crops: Spectral comparison with portable spectroradiometer measurements. Photogramm. Fernerkun 2015, 69–79. [Google Scholar] [CrossRef]
- Burkart, A.; Aasen, H.; Alonso, L.; Menz, G.; Bareth, G.; Rascher, U. Angular dependency of hyperspectral measurements over wheat characterized by a novel UAV based goniometer. Remote Sens. 2015, 7, 725–746. [Google Scholar] [CrossRef] [Green Version]
- Hui, B.; Wen, G.; Zhao, Z.; Li, D. Line-scan camera calibration in close-range photogrammetry. Opt. Eng. 2012, 51, 053602. [Google Scholar] [CrossRef]
- Draréni, J.; Roy, S.; Sturm, P. Plane-based calibration for linear cameras. Int. J. Comput. Vis. 2011, 91, 146–156. [Google Scholar] [CrossRef]
- Savage, P.G. Blazing gyros: The evolution of strapdown inertial navigation technology for aircraft. J. Guid. Control Dyn. 2013, 36, 637–655. [Google Scholar] [CrossRef]
- Zhang, Z. Determining the epipolar geometry and its uncertainty: A review. Int. J. Comput. Vis. 1998, 27, 161–195. [Google Scholar] [CrossRef]
- Sarbolandi, H.; Lefloch, D.; Kolb, A. Kinect range sensing: Structured-light versus time-of-flight kinect. Comput. Vis. Image Underst. 2015, 139, 1–20. [Google Scholar] [CrossRef]
- Thibos, L.N.; Bradley, A.; Still, D.L.; Zhang, X.; Howarth, P.A. Theory and measurement of ocular chromatic aberration. Vis. Res. 1990, 30, 33–49. [Google Scholar] [CrossRef]
- Paulus, S.; Dupuis, J.; Mahlein, A.-K.; Kuhlmann, H. Surface feature based classification of plant organs from 3D laserscanned point clouds for plant phenotyping. BMC Bioinf. 2013, 14, 238. [Google Scholar] [CrossRef] [PubMed]
- Chéné, Y.; Rousseau, D.; Lucidarme, P.; Bertheloot, J.; Caffier, V.; Morel, P.; Belin, É.; Chapeau-Blondeau, F. On the use of depth camera for 3D phenotyping of entire plants. Comput. Electron. Agric. 2012, 82, 122–127. [Google Scholar] [CrossRef] [Green Version]
- Vos, J.; Evers, J.; Buck-Sorlin, G.; Andrieu, B.; Chelle, M.; De Visser, P. Functional–structural plant modelling: A new versatile tool in crop science. J. Exp. Bot. 2010, 61, 2101–2115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, L.; Henke, M.; Zhu, J.; Kurth, W.; Buck-Sorlin, G. A functional–structural model of rice linking quantitative genetic information with morphological development and physiological processes. Ann. Bot. 2011, 107, 817–828. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuska, M.; Wahabzada, M.; Leucker, M.; Dehne, H.-W.; Kersting, K.; Oerke, E.-C.; Steiner, U.; Mahlein, A.-K. Hyperspectral phenotyping on the microscopic scale: Towards automated characterization of plant–pathogen interactions. Plant Methods 2015, 11, 14. [Google Scholar] [CrossRef] [PubMed]





| Parameter Setting | Value |
|---|---|
| Start position (inch) | 0.8 |
| End position (inch) | 9.2 |
| Scan Speed (inch/ms) | 0.55 |
| Framerate (Hz) | 60.000 |
| Integration time (ms) | 7–500 |
| Reference Points | Kinect V2 3D Coordinate | System 3D Coordinate | ||||
|---|---|---|---|---|---|---|
| X Axis | Y Axis | Z Axis | X Axis | Y Axis | Z Axis | |
| 1 | 24.08 | −16.99 | 683 | 10.87 | 11.11 | 762 |
| 2 | −156.3 | −17.685 | 676.5 | 190.87 | 11.51 | 755.5 |
| 3 | −159.55 | 117.55 | 674 | 191.17 | 141.48 | 753 |
| 4 | 23.825 | 116.15 | 677.25 | 11.17 | 141.11 | 756.25 |
| 5 | −27.785 | 32.605 | 631.5 | 59.04 | 62.94 | 710.5 |
| 6 | −108.1 | 32.3675 | 628.25 | 142.76 | 63.03 | 707.25 |
| 7 | −107.65 | 112.4 | 626.75 | 142.79 | 140.26 | 705.25 |
| 8 | −27.4878 | 112.5 | 626.25 | 59.11 | 140.26 | 705.25 |
| Reference Points | u | v | x | y | z |
|---|---|---|---|---|---|
| 1 | 42.24763 | 49.61491 | 24.08 | −16.99 | 683 |
| 2 | 760.5121 | 51.39052 | −156.3 | −17.685 | 676.5 |
| 3 | 759.041 | 631.5677 | −159.55 | 117.55 | 674 |
| 4 | 44.43668 | 630.1391 | 23.825 | 116.15 | 677.25 |
| 5 | 234.8244 | 280.9727 | −27.785 | 32.605 | 631.5 |
| 6 | 567.7642 | 281.352 | −108.1 | 32.3675 | 685.25 |
| 7 | 567.8614 | 626.1389 | −107.65 | 112.4 | 626.75 |
| 8 | 235.0701 | 626.13 | −27.4875 | 112.5 | 626.25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, P.; Luo, X.; Jin, J.; Wang, L.; Zhang, L.; Liu, J.; Zhang, Z. Improving High-Throughput Phenotyping Using Fusion of Close-Range Hyperspectral Camera and Low-Cost Depth Sensor. Sensors 2018, 18, 2711. https://doi.org/10.3390/s18082711
Huang P, Luo X, Jin J, Wang L, Zhang L, Liu J, Zhang Z. Improving High-Throughput Phenotyping Using Fusion of Close-Range Hyperspectral Camera and Low-Cost Depth Sensor. Sensors. 2018; 18(8):2711. https://doi.org/10.3390/s18082711
Chicago/Turabian StyleHuang, Peikui, Xiwen Luo, Jian Jin, Liangju Wang, Libo Zhang, Jie Liu, and Zhigang Zhang. 2018. "Improving High-Throughput Phenotyping Using Fusion of Close-Range Hyperspectral Camera and Low-Cost Depth Sensor" Sensors 18, no. 8: 2711. https://doi.org/10.3390/s18082711
APA StyleHuang, P., Luo, X., Jin, J., Wang, L., Zhang, L., Liu, J., & Zhang, Z. (2018). Improving High-Throughput Phenotyping Using Fusion of Close-Range Hyperspectral Camera and Low-Cost Depth Sensor. Sensors, 18(8), 2711. https://doi.org/10.3390/s18082711






