Abstract
In the future, phasor measurement units are expected to be applied in distribution networks (DNs) for their control and monitoring. Because of the widely used power electronic devices in DNs, harmonics are widely present in a voltage/current signal. Particularly, second harmonics have the most significant uncertainty contributions to synchrophasor estimation, which is especially true when a short cycle observation window is used for a fast response. Based on the interpolated dynamic discrete Fourier transform (IpDFT), this paper introduces an enhanced IpDFT (e-IpDFT) synchrophasor estimator that considers second harmonic interferences. First, the adaptive equivalent filters of the IpDFT are given. Based on these, the optimal frequencies where the IpDFT has the least second harmonic interferences are then searched using an enumeration method, and the e-IpDFT synchrophasor estimator is accordingly proposed. Instantaneous frequency responses and several simulation tests show that the e-IpDFT performs much better than the IpDFT in second harmonic suppression, and can meet the P-class response time requirements and most of the M-class accuracy requirements of the IEEE standard C37.118.1 only over a three-cycle window.
1. Introduction
Nowadays, the power flows in distribution networks (DNs) become bidirectional due to the increasing penetrations of distributed energy resources (DERs) (e.g., photovoltaic power generation systems and energy storage systems) in power systems. It is necessary to accurately measure voltage/current phasors, frequencies and even rate of change frequencies (ROCOFs) for DN monitoring and control. To this end, phasor measurement units (PMUs) widely used in transmission networks (TNs) are also expected to be applied in DNs.
According to the IEEE standard C37.118.1-2011 and its amendment standard C37.118.1a-2014 (collectively called the Standard in the following) [1,2], PMUs are divided into two classes for TNs: (1) P-class for fast response applications (i.e., protection); and (2) M-class for high accuracy applications (i.e., measurement and monitoring). In DNs, a PMU is expected to have the above two abilities simultaneously. On the one hand, voltage dips and swells occur frequently in DNs, which requires that PMUs should estimate synchrophasors only over a few cycles. In addition, PMU-based fast fault diagnose and location applications in DNs need fast synchrophasor estimates. On the other hand, large harmonic distortions and frequency deviations can be present in DNs [3,4,5], which requires that PMUs should be robust to large disturbances. However, it is a big challenge to meet these two requirements simultaneously. Harmonic interferences are non negligible in this complex scenario, which is especially true when large frequency deviations are also present in a voltage/current signal [3,4]. Particularly, second harmonics, which can be very high in DNs due to the high penetration of DERs, have the most significant uncertainty contributions [6].
Traditionally, many methods have been proposed to estimate synchrophasors with the consideration of frequency deviations and oscillations [3,7,8,9,10,11,12,13,14]. For example, as for frequency deviations, a very useful tool is the well-known interpolated discrete Fourier transform (IpDFT) [7] and its enhanced version [8]. Regarding oscillations, the Taylor series expansion is widely used in the literature to describe oscillating signals, such as the least square [9], the weighted least square (WLS) [10], the Taylor-DFT [11,12,13], the Taylor-Kalman filter [14] and the interpolated dynamic DFT (IpDFT) [3]. However, few of these papers have considered second harmonic interferences. Typically, the IpDFT is one of the most accurate synchrophasor estimators under oscillation and large frequency deviation conditions [3]. It can obtain synchrophasor, frequency and ROCOF based on the phasor derivative estimates. However, because the second harmonic is the harmonic closest to the window spectrum main lobe, the attenuation around the second harmonic frequency is the lowest. Thus, the IpDFT suffers from second harmonic interferences, which is especially true when large frequency deviations are also present.
The widely used DFT can suppress second harmonic interferences significantly under synchronous sampling conditions [15]. However, under nonsynchronous conditions, large errors will arise because of the effects of spectral leakage and second harmonic interferences [16]. Recently, a series of methods was proposed to estimate synchrophasors considering second harmonic interferences, such as the improved WLS method [4], the Taylor–Kalman–Fourier filter [17], the Taylor–Fourier transform (TFT) and its improved version [18], i.e., the adaptive TFT [19,20,21]. For example, synchrophasor estimation filters that have a notch filter effect at the second harmonic frequency are designed by the TFT. However, under large frequency deviations, large errors will arise because the second harmonic cannot be filtered clearly. Although the adaptive TFT has a wide stop band around the second harmonic frequency, it needs high computational cost or large memory to calculate filters online or store filters.
In this paper, an enhanced IpDFT (e-IpDFT) synchrophasor estimator is proposed considering second harmonic interferences. It only uses a two- or three-cycle data window, and thus its response time is extremely short. It can sufficiently suppress second harmonic interferences, even when large frequency deviations and oscillations are also present. Although higher order harmonics can also be significant in DNs, these harmonics can be suppressed by adopting a suitable window function, e.g., the Hanning window [4]. Interharmonics can also be significant in DNs. Nevertheless, this paper focuses on second harmonic suppression.
2. e-IpDFT Synchrophasor Estimator
This section introduces the e-IpDFT synchrophasor estimator. First, the classical IpDFT is briefly recalled. Then, the adaptive equivalent filters of the IpDFT are given. Next, the optimal frequencies used in the IpDFT with the least second harmonic interferences are found based on these filters, and the e-IpDFT is accordingly proposed. Finally, the implementation steps of the e-IpDFT are summarized.
2.1. Signal Model
Generally, a dynamic signal can be expressed as
where represents the operation selecting the real part of its argument; f is the actual fundamental frequency; and and are the fundamental amplitude and phase oscillations, respectively. Please note that f may differ from the nominal fundamental frequency with a static frequency deviation , i.e., . According to [1], a synchrophasor is defined as a phasor referred to the nominal fundamental frequency, which is given by
where is the so called raw synchrophasor.
2.2. Classical IpDFT
Assume Equation (1) is sampled at sampling rate , and samples are obtained in an observation window centered at time , where is the sample number of a nominal cycle. Thus, the integer nominal cycle number of the observation window is . Please note that, to make lie in the center of the observation window, should be an odd number. The Taylor series expansion is used to approximately express with a Kth-order truncation [9]. Then, the signal around time can be approximately expressed as
where the superscript represents the conjugate operation; and is the kth-order derivative of calculated at time . Computing the windowed discrete-time Fourier transform (DTFT) of Equation (3), we have
where (with ) is a bin frequency (with and ), is a window function, and
is a function related to the derivative order k (with k = 0, 1, ..., K) and (with ). Truncate the Taylor series expansion to the second order (). Then, Equation (4) can be rearranged as
with being a column vector containing the windowed DTFT of at the three bin frequencies; and being two column vectors containing and its conjugate phasor (with ), respectively; and and being two matrices containing and computed at different orders k (with ) and different frequencies (with ). Additionally, Equation (6) can be rearranged as
where is a matrix consisting of , and their conjugate matrices; is a column vector consisting of the two vectors and ; and is a column vector consisting of two vectors and . Obviously, because the three bin frequencies used in the windowed DTFT are unequal, is a full rank matrix. Then, can be easily estimated by
Thus, the raw synchrophasor and its derivatives and are obtained. Then, the fundamental frequency and ROCOF can be estimated by [9]
where represents the operation selecting the imaginary part of its argument. Accordingly, the frequency deviation can be estimated by
In this way, the estimated synchrophasor can be obtained according to Equation (2). It should be noted that the actual fundamental frequency f is usually unknown. It is originally assumed as and then three iterations are needed to get an accurate estimate [3].
Obviously, the second harmonic interferences are not considered in [3]. If the second harmonic is significant, it will lead to a large interference component in , and large differences will be present between and . As a result, large errors will arise (see Equation (7)). Compared with other harmonics, the second harmonic is closest to the window spectrum main lobe. Thus, it has the most significant uncertainty contribution to synchrophasor estimation.
2.3. Adaptive Equivalent Filters of the IpDFT
As is well known, PMU is a typical discrete-time system, and a PMU using the IpDFT method can be seen as a linear time-invariant system during each iteration. Thus, during each iteration, the phasor derivative (, and ) estimators can be equivalent to three digital finite-impulse-response (FIR) filters. Then, the ability of second harmonic interference suppression of the IpDFT can be evaluated based on these adaptive equivalent filters. Consider that, in Equation (8), can be expressed in linear convolution, which is given by
where ⊗ denotes the operation of linear convolution, and
is the equivalent filter of the windowed DTFT. Assume the six row vectors of the matrix are (with ); represents the q-th element of , which is related to and , and can be seen as the gain of the corresponding DTFT value ; represents the ()-th element of , i.e., the phasor derivatives and their conjugate phasors. Then, Equation (8) can also be expressed as
In this way,
are the adaptive equivalent FIR filters for , and estimation, respectively. According to Equations (4), (13) and (15), these filters are related to the three DTFT frequencies (with ) and the fundamental frequency f. During each iteration, the IpDFT modifies the fundamental frequency f in its signal model, and (or ) is recalculated. Then, the adaptive equivalent filters are redesigned.
Theoretically, if any three different frequencies around f are used in the windowed DTFT, will be a full rank matrix, and Equation (7) can be successively solved. Thus, not only the bin frequencies but also other three frequencies around f can be used to design the above adaptive filters. Obviously, when different DTFT frequencies are used, there will be different second harmonic interference components in . That is also to say, the adaptive filters (thus the IpDFT) will have different performances on second harmonic suppression [22]. Thus, we can find optimal DTFT frequencies to design adaptive filters with the strongest second harmonic suppression. Then, the total vector error (TVE), frequency error (FE) and ROCOF error (RFE) will be controlled at a low level.
2.4. DTFT Frequency Selection for Accuracy Enhancement of the IpDFT
This subsection first selects the optimal DTFT frequencies for the no frequency deviation condition, i.e., . Then, the solution to the frequency deviation condition is given.
When , the IpDFT does not need any iteration. Then, it is true that the IpDFT can be seen as a bank of FIR filters given in Equation (15) (no longer the adaptive ones). We can use the frequency responses of these equivalent filters to evaluate the TVE, FE and RFE of the IpDFT. According to [23], if Equation (1) is stationary (i.e., the fundamental magnitude and phase oscillations are ignored), the relationship between the IpDFT’s TVE (FE or RFE) and its frequency response can be given by (see Appendix A).
where (with ) represents the frequency response of (with ) at frequency f; and r is the magnitude ratio of the second harmonic to the fundamental. After some algebra and simplifications (see Appendix B), Equations (16)–(18) can be rewritten as
Thus, the IpDFT’s TVE, FE and RFE upper bounds are mainly determined by the filters’ attenuation at the second harmonic frequency. Based on the enumeration method, three optimal frequencies can be found to minimize the sum of the TVE, FE and RFE upper bounds, i.e.,
The implementation details of the enumeration method are as follows. Generally, to make a full rank matrix, the three frequencies cannot be the same. In this paper, the minimum deviations between each of the two frequencies are set at 1 Hz. Additionally, to reduce the infiltration from the image fundamental tone and second harmonic component [6], the three frequencies need to be close to f. In this paper, they are limited in a frequency band of (25, 75) Hz. Finally, the step for optimal frequencies searching is set at 0.2 Hz.
It should be highlighted that the optimal frequencies are for the no frequency deviation condition. However, in practice, the fundamental frequency frequently deviates from the nominal value. To deal with this problem, we can take the following measures:
- Compute and using the optimal frequencies of the no frequency deviation condition, and estimate the actual fundamental frequency f using Equation (9).
- Modify as (with ), and recompute and to estimate the actual fundamental frequency again.
- Repeat the above two steps twice (i.e., another two iterations) for high accuracy.
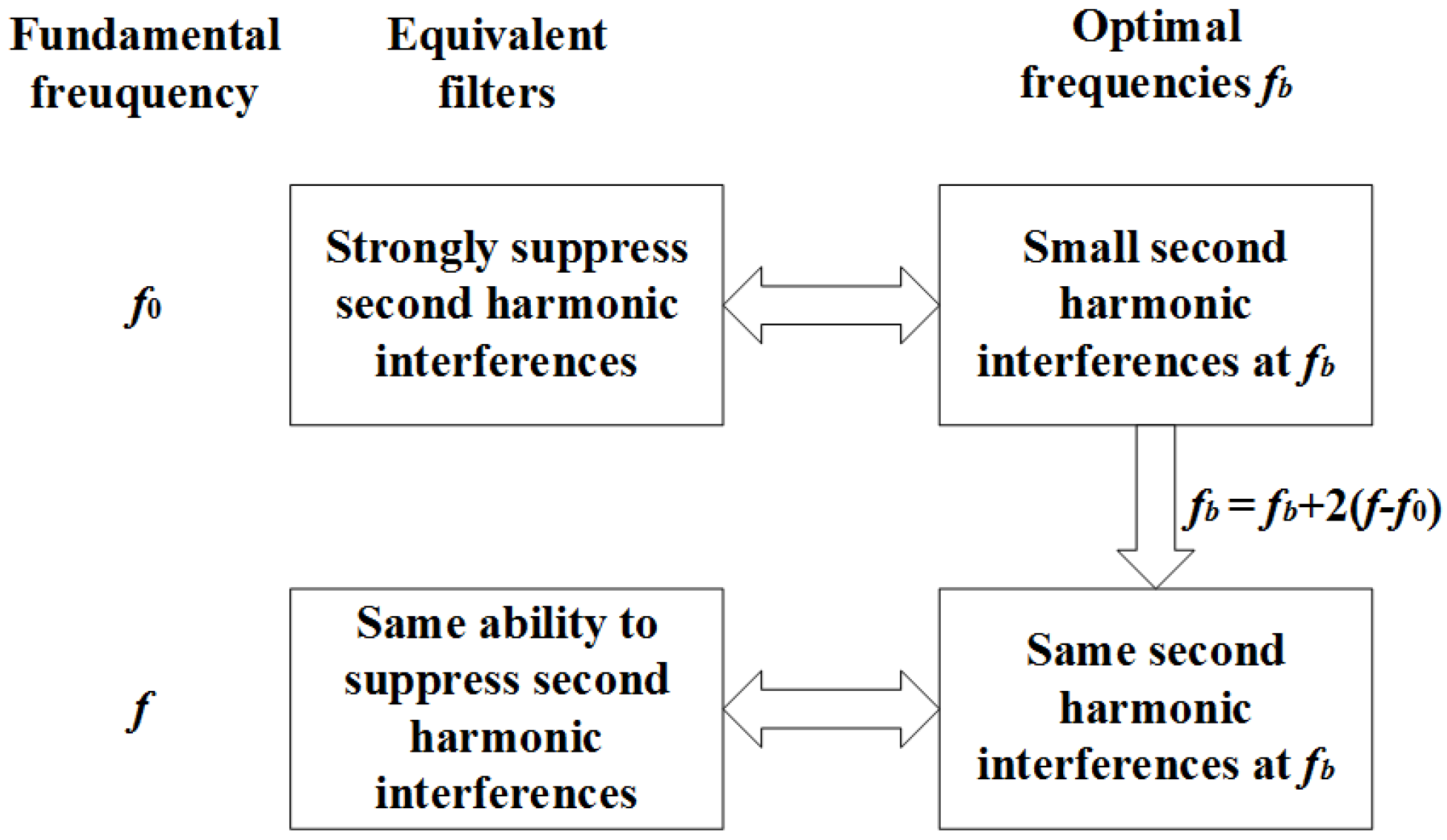
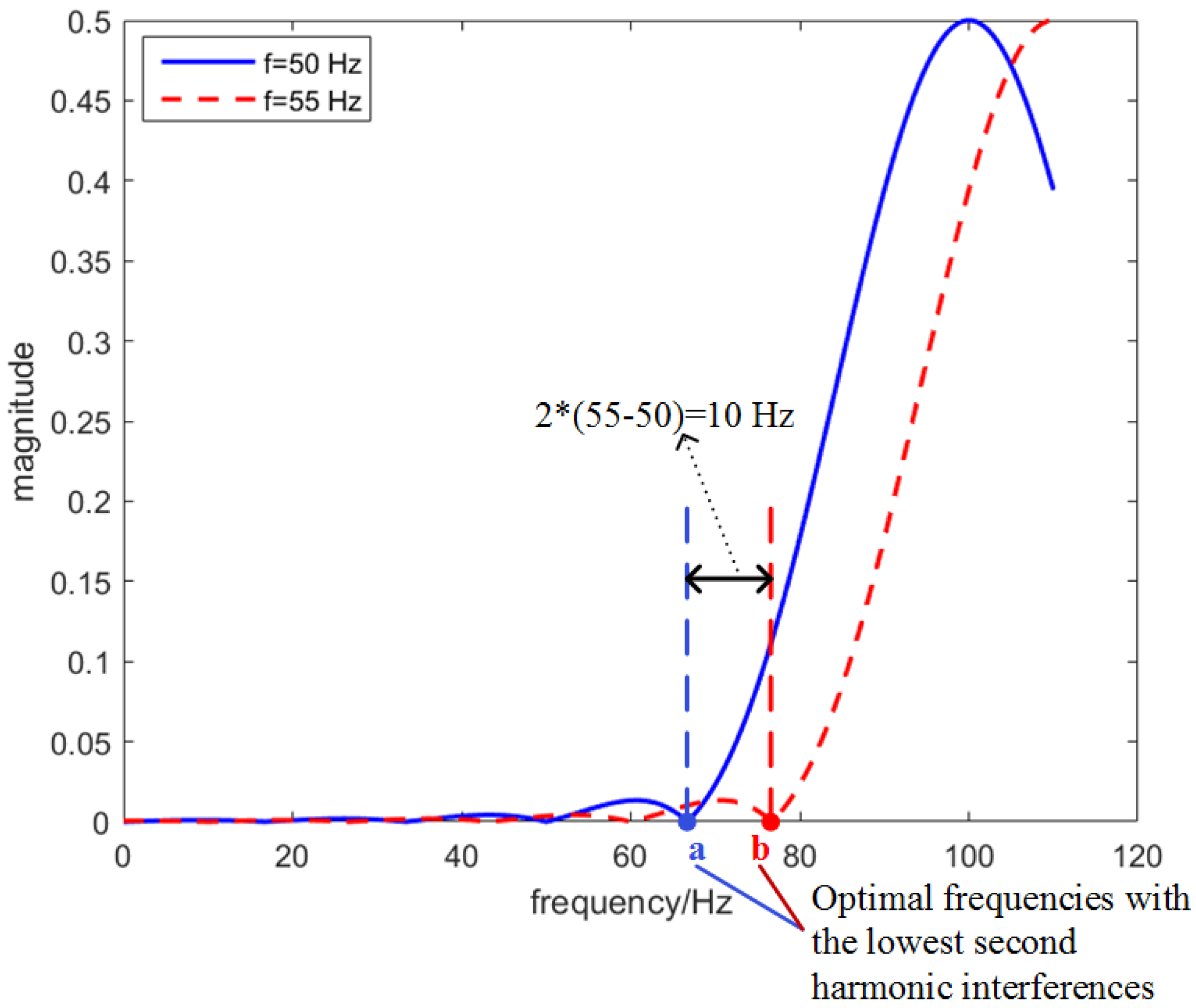
In this way, the new adaptive filters will have similar second harmonic suppression abilities as the filters for the no frequency deviation condition. The reason is shown in Figure 1 and Figure 2. When the adaptive equivalent filters can sufficiently suppress second harmonic interferences, it is equivalent to the second harmonic interferences at being very small (see the red line in Figure 2) [22]. When the fundamental frequency has a deviation of , the new optimal frequencies should deviate with a deviation of to keep the ability of second harmonic suppression (see the blue and red bins in Figure 2).
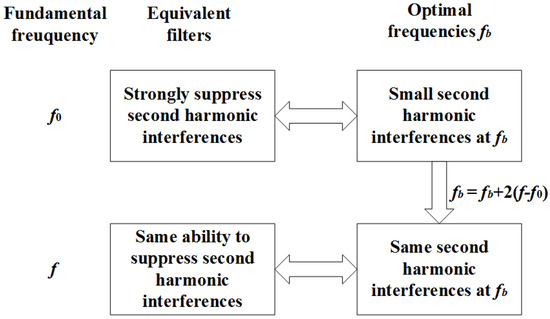
Figure 1.
Illustration of the principle.
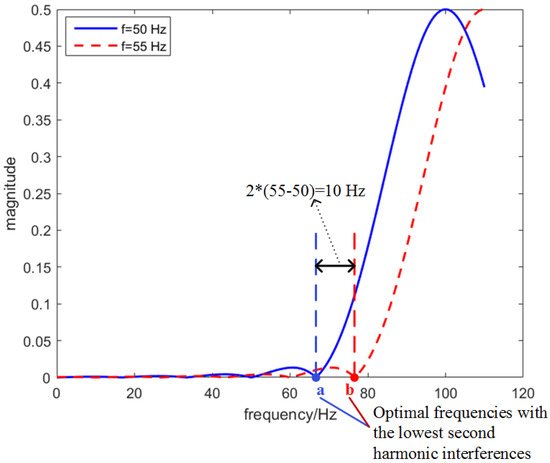
Figure 2.
Illustration of the second harmonic interference. The red and blue lines are second harmonic interferences at different frequencies. The image second harmonic component is ignored. Only one bin used in the IpDFT is illustrated.
In Table 1, the optimal DTFT frequencies for the no frequency deviation condition are listed. In this paper, short cycle windows, i.e., two- and three-cycle windows, are considered for fast responses. The Hanning and Hamming windows are both adopted for illustration. In Table 1, we can see that the optimal DTFT frequencies for two-cycle windows (both the Hanning and Hamming window) are very small. This is because the DTFT values at small frequencies will have small interferences from second harmonics (see Figure 2).

Table 1.
Optimal DTFT frequency sets for different windows and window lengths with . The sampling frequency is set at 2000 Hz (for 50-Hz system).
2.5. Implementation Steps of the e-IpDFT
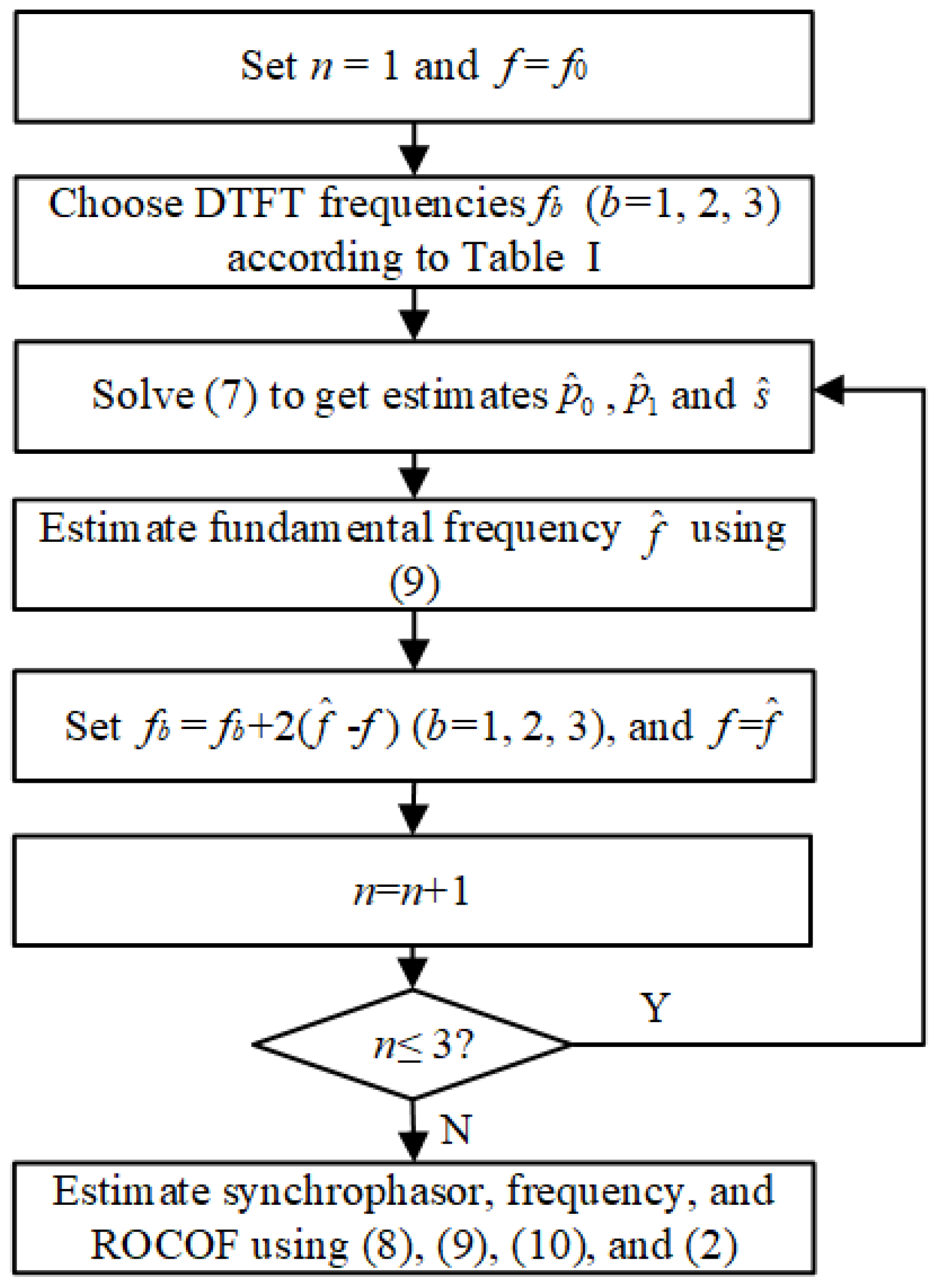
The implementation steps of the e-IpDFT are summarized in Figure 3. To suppress second harmonic interferences under frequency deviation conditions, a first estimation of fundamental frequency should be carried out, and then the three DTFT frequencies are adaptively modified. In this way, the estimated fundamental frequency is not only used in signal model foundation but also in DTFT frequency modification. For a high accuracy, we take three iterations to modify the fundamental frequency and thus the DTFT frequencies.
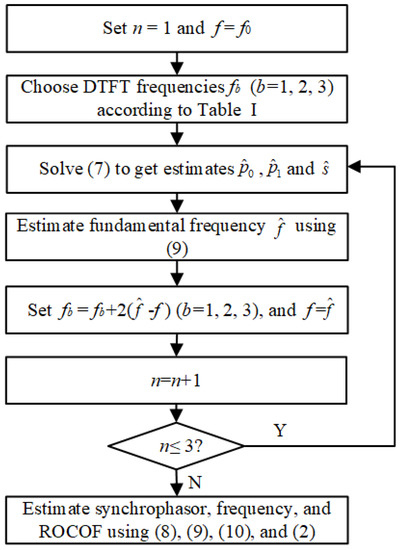
Figure 3.
Implementation steps of the e-IpDFT.
Based on the optimal DTFT frequency selection and adaptive modification, the e-IpDFT can suppress second harmonic interferences. Even when the second harmonic interferences and frequency deviations occur simultaneously, the e-IpDFT can still estimate the synchrophasor, frequency and ROCOF with a high accuracy.
2.6. Computational Complexity
The main computations of the e-IpDFT and IpDFT are generating matrices (, ) and solving Equation (7). Assume there are samples in the observation window; the iteration number is n; and the Taylor truncation order is . Then, the main computations of the two methods are listed in Table 2. Compared with the IpDFT, the e-IpDFT’s DTFT frequencies are adaptively modified at each iteration. Thus, the DTFT computation will change at each iteration, and the computation time of the e-IpDFT will be longer than the IpDFT. However, because only three iterations are carried out, the overall complexity of the e-IpDFT will still be quite small. If , then the overall floating-point operations of the two- and three-cycle e-IpDFT are only 45,468 and 94,122, respectively. Thus, even if a low performance digital signal processor is used, the computation time will still be very short.

Table 2.
Computational complexity of the e-IpDFT and IpDFT. The computation types + and × denote complex addition and multiplication, respectively.
3. Instantaneous Frequency Response
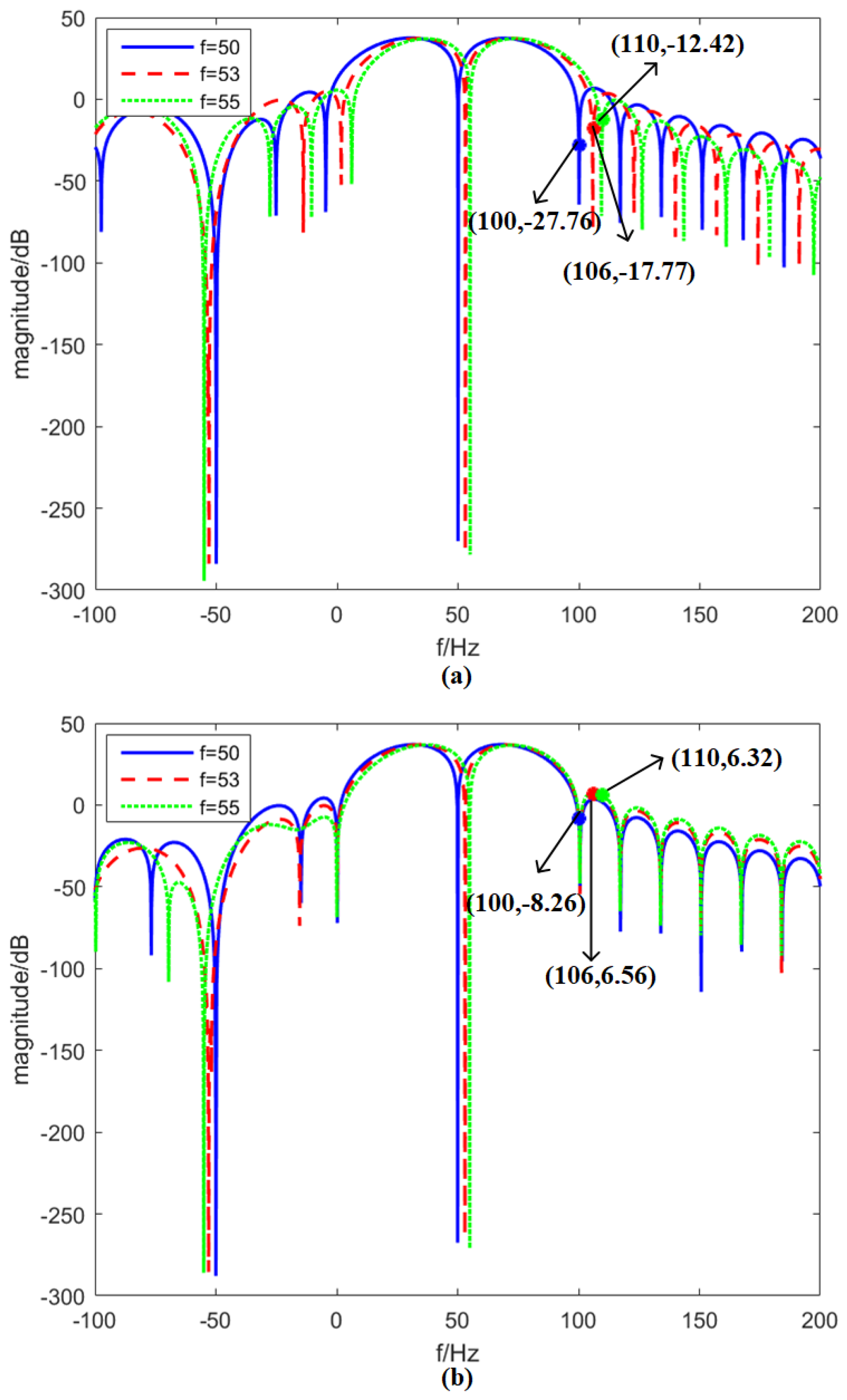
This section mainly compares the performances of the IpDFT and e-IpDFT for second harmonic suppression. In Figure 4, the instantaneous frequency responses of the e-IpDFT and IpDFT are shown. As is known, frequency and ROCOF estimates are more sensitive to second harmonic interferences. This section selects the filter on estimation for illustration. In Figure 4a, we can see that, when the fundamental frequency is set at 50, 53 and 55 Hz, the second harmonic attenuation of the e-IpDFT’s adaptive equivalent filter is 27.76, 17.77 and 12.42 dB, respectively. By contrast, the second harmonic attenuation of the IpDFT’s adaptive equivalent filter is only 8.26, −6.56 and −6.32 dB, respectively (see Figure 4b). The second harmonic attenuation of the e-IpDFT’s adaptive equivalent filter is always bigger than 10 dB, and is about 20 dB larger than the IpDFT’s. This evidence shows that the e-IpDFT can suppress second harmonic interferences, even under large frequency deviation conditions.
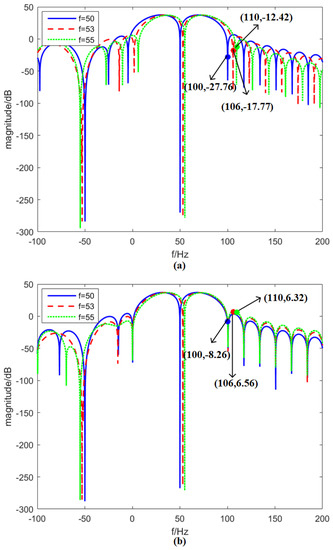
Figure 4.
Instantaneous frequency response of the e-IpDFT and IpDFT for estimation. The three-cycle Hanning window is chosen for illustration. f is set at 50, 53 and 55 Hz, respectively: (a) e-IpDFT; and (b) IpDFT.
It is interesting that Figure 4a,b shows different shapes around second harmonic frequency. The reason is shown in Figure 1 and Figure 2. When different frequencies are used in the IpDFT, the DTFT values in will have different interferences from the second harmonic. If the optimal frequencies are used, the interferences will be very small, and the adaptive equivalent filters can strongly suppress the second harmonic. Moreover, under frequency deviation conditions, the optimal frequencies will be adaptively modified, and the second harmonic will still be sufficiently suppressed.
4. Simulation Tests
To evaluate and compare the performances of the e-IpDFT and IpDFT, a series of simulation tests are carried out. First, canonical tests stated in the Standard are carried out to show that the e-IpDFT can meet basic requirements of the Standard. Next, peculiar conditions where multiple disturbances occur simultaneously are considered to show the e-IpDFT’s robustness to large second harmonic interferences. Finally, a real world example is taken to show the practical values of the e-IpDFT.
More details about the tests are as follows. (1) Two- and three-cycle windows are particularly considered in this paper. (2) The Hanning and Hamming windows are both adopted for illustration. (3) All test signals are sampled at 2000 Hz (for 50-Hz system). (4) The initial phases of all possible components (e.g., the fundamental and the second harmonic) are randomly selected within rad. (5) At distribution level, the level of harmonics or other disturbances can be very high. Thus, all signal parameters, such as frequency deviation, harmonic distortion level, modulation level, modulation frequency and linear frequency ramp rate, are set at the maximum values of M-class tests stated in the Standard (corresponding to the worst conditions). (6) As for accuracy tests, the M-class TVE, FE and RFE limits in the Standard are referred with reporting rate = 50 frames/s (in China, is generally set at 50 frames/s). (7) Regarding responsiveness tests, the P-class response time limits in the Standard are referred for transient tests.
4.1. Canonical Tests
In this subsection, a set of canonical tests stated in the Standard, including frequency deviation, harmonic distortion, amplitude and phase modulations (AM + PM), frequency ramp and step changes, are carried out to verify the performances of the proposed method. The corresponding results are shown in Table 3. As shown, although sometimes the results of the e-IpDFT are worse than the IpDFT, they are always much smaller than the corresponding limits. In this respect, the e-IpDFT can be used for practical applications. The differences between the results of the e-IpDFT and IpDFT are caused by their different instantaneous frequency responses.

Table 3.
Canonical test results and the corresponding thresholds in the standard. The Hanning window is adopted in the e-IpDFT and IpDFT. The observation window is three cycles long. The results of the amplitude step change test are expressed in nominal cycles. In other tests, the TVEs (%), |FE|s (Hz) and |FE|s (Hz/s) are given in maximum values.
In addition to the above tests, out-of-band interferences with frequencies within the interval [10, and should also be considered to test the proposed method. These frequencies are close to the optimal frequencies and the bin frequencies, which makes the interferences too high. As a result, neither the e-IpDFT nor the IpDFT can meet the Standard’s requirements. The performances of the e-IpDFT are similar to the IpDFT as reported in [3]. These interferences can be suppressed by adopting a long observation window [3], but this is not the subject of this paper.
4.2. Frequency Deviation + Second Harmonic
In DNs, frequency deviations and second harmonic interferences may occur simultaneously. To test the proposed method’s robustness to this condition, a signal with a -Hz frequency deviation (f = 45 Hz) and a 10% second harmonic is considered. In the following, the abbreviation “frequency deviation + second harmonic” is used to denote the test defined above. Similar abbreviations used in the following have the similar meanings. This is the worst test condition stated in the Standard.
The maximum TVEs, |FE|s and |RFE|s returned by the e-IpDFT and IpDFT are shown in Table 4. In Table 4, we can see that the e-IpDFT is much more accurate than the IpDFT. This is because the e-IpDFT can select optimal frequencies and adaptively modify them under frequency deviations. Thus, even under large frequency deviations, the e-IpDFT can still sufficiently suppress the second harmonic interferences. Additionally, when a three-cycle window is used, the maximum TVEs, |FE|s and |RFE|s of the e-IpDFT are much smaller than the related limits of the Standard. In this respect, the e-IpDFT has a better performance than the IpDFT, which needs a four-cycle window to achieve the same performance [3].

Table 4.
Maximum TVEs (%), |FE|s (Hz) and |RFE|s (Hz/s) returned by the e-IpDFT and IpDFT in the “frequency deviation + second harmonic” test. Gray cells refer to the results beyond the boundaries of the M-class requirements of the standard.
4.3. Frequency Deviation + Second Harmonic + Modulation
In this subsection, another complex scenario that may occur in DNs is considered. Specifically, not only the −5-Hz frequency deviation and 10% second harmonic but also the fundamental amplitude and phase modulations are considered. The modulation level and frequency are set at 0.1 and 5 Hz, respectively. According to the Standard, this is also the worst condition for such a test.
In Table 5, the results returned by the e-IpDFT and IpDFT under such condition are shown. Please note that the e-IpDFT is much more accurate than the IpDFT because it can significantly suppress second harmonic interferences. In addition, the maximum TVEs, |FE|s and |RFE|s returned by the three-cycle e-IpDFT are still smaller than the corresponding limits of the Standard.

Table 5.
Maximum TVEs (%), |FE|s (Hz) and |RFE|s (Hz/s) returned by the e-IpDFT and IpDFT in the “frequency deviation + second harmonic + modulation” test. The meaning of the gray cells is the same as in Table 4.
4.4. Other Complex Scenarios
In some complex scenarios, not only the second harmonics but also the third or higher-order harmonics may be present in a voltage/current signal. Generally, only the second and third harmonics have strong impacts on synchrophasor estimation. Higher-order harmonics can be sufficiently suppressed by the Hanning window [4]. Meanwhile, additive wide band noise should also be considered. In this subsection, two typical scenarios are considered: (a) joint effects of -Hz frequency deviation, 10% second harmonic and third harmonic; and (b) joint effects of -Hz frequency deviation, 10% second harmonic and 60-dB noise.
The TVEs, |FE|s and |RFE| of both methods (maximum in Scenario (a), mean and standard deviation values in Scenario (b)) are reported in Table 6. Compared with Table 4, several conclusions can be drawn. Although the third harmonic or wide band noise are also present, the three-cycle e-IpDFT can still meet the corresponding requirements of the Standard. However, the IpDFT cannot meet the corresponding requirements. In the test of “Fre. Dev. + 2nd Harm. + 60 dB Noise”, the e-IpD2FT with respect to the IpD2FT shows a remarkable performance improvement for the RFE. When in the presence of second harmonics and frequency deviation, large interferences will be present at bin frequencies, whereas they are negligible at the adaptive selected frequencies. Because the RFE is the rate of FE, it is more sensitive to such interferences. As a result, the e-IpDFT has much smaller |RFE|s (mean and standard deviation values) than the IpDFT.

Table 6.
TVEs (%), |FE|s (Hz) and |RFE|s (Hz/s) returned by the e-IpDFT and IpDFT. The Hanning window is adopted in the e-IpDFT and IpDFT. The observation window is three cycles long. The TVE, FE and RFE limits in the standard are the same as in Table 4. The meaning of the gray cells is the same as in Table 4.
4.5. Sampling Rate
As is known, the optimal frequencies given in Table 1 are obtained in a sampling frequency of 2000 Hz. In this subsection, the performances of the e-IpDFT under different sampling rates are tested (2000, 2400, 4000 and 4800 Hz). The fundamental frequency is set at 51 Hz (1-Hz frequency deviation), and the magnitude ratio of the second harmonic to the fundamental is set at 5%.
The results are shown in Table 7. As shown, although the sampling rate varies, the maximum TVEs, |FE|s and |RFE|s returned by the e-IpDFT do not have any variation. By contrast, the results returned by the IpDFT have a few changes. The reason is as follows. For the e-IpDFT, the DTFT frequencies are the same in all tests. However, the IpDFT modifies its DTFT frequencies ( and ) with the sampling rate variations. Thus, the DTFT values () of the e-IpDFT are the same in all tests, whereas the DTFT values of the IpDFT are not the same. Anyway, the e-IpDFT is robust to sampling rate variations.

Table 7.
Results (maximum values) returned by the e-IpDFT and IpDFT under different sampling rates. The TVE, FE and RFE limits in the standard are the same as in Table 4.
4.6. A Real World Example
To demonstrate the real benefit of the e-IpDFT, a real world example in industry is taken in this paper. According to [24], transformer current during inrush can have a second harmonic up to 63% of the fundamental. Meanwhile, higher-order harmonics can also be present. In this subsection, such a complex scenario is considered. Harmonic levels are set according to [24] (see Table 8). The fundamental frequency is set at 49 Hz, and 60 dB wide band noise is added to the signal. Accordingly, the results are reported in Table 9. We can see that, even under such large harmonic disturbance conditions, the mean TVE, |FE| and |RFE| of the e-IpDFT are only 0.55%, 0.01 Hz and 0.98 Hz/s, respectively, which are smaller than the corresponding limits of the Standard. However, the IpDFT cannot meet the corresponding requirements. This example shows the significant practical values of the e-IpDFT.

Table 8.
Harmonic components of the test signal.
5. Conclusions
This paper proposes a novel synchrophasor estimator, especially for DNs, where the most significant uncertainty contribution is the second harmonic. The adaptive equivalent filters of the IpDFT are given in this paper, which are used for finding optimal frequencies. The e-IpDFT has a fast response, and can meet P-class response time requirements because only a few cycles are used. In addition, it has a high accuracy, and can meet most of the M-class accuracy requirements only over a three-cycle observation window, even when oscillation, large frequency deviation and harmonic distortions occur simultaneously in a voltage/current signal. A real world example is taken to show the real benefit of the e-IpDFT.
Author Contributions
Conceptualization, L.C.; Formal analysis, L.C.; Funding acquisition, W.Z.; Methodology, L.C. and F.W.; Project administration, S.H.; Supervision, W.Z. and F.W.; Validation, L.C.; Writing—original draft, L.C.; and Writing—review and editing, Q.W.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proof of Equations (16)–(18)
A stationary voltage/current signal containing the fundamental and second harmonic components can be defined as
where and denote the amplitudes of the fundamental and the second harmonic, respectively; and denote the phases of the fundamental and the second harmonic, respectively; and are the fundamental and the second harmonic phasors, respectively; and and denote the fundamental and the second harmonic, respectively. Assume is the static fundamental frequency deviation, i.e., (with being the nominal fundamental frequency). According to the IEEE standard [1], the synchrophasor is defined as a phasor referred to the nominal fundamental frequency, i.e., . Please note that due to the possible frequency deviation, the synchrophasor should be a time function, even though the fundamental phasor is a constant. Because is a constant, the i-th order derivative of the synchrophasor is
Then, the synchrophasor derivative estimates are as follows:
where is the ideal filter for the estimation of the i-th order synchrophasor derivative, it should have ideal frequency responses as follows:
and is the estimation error of , which is given by
Additionally, according to Equations (A3) and (A5), we can obtain
where is the difference between and , which is given by
According to Equations (9) and (10), after some algebra, the TVE, FE and RFE of the estimator can be given by [23]
where denotes negligible high-order term of . Thus, we can obtain
where (with ) represents the frequency response of (with ) at the fundamental frequency ; and is the magnitude ratio of the second harmonic to the fundamental. Please note that the denominator in Equations (A11)–(A13) is reduced since . Additionally, the “” part becomes “” because the imaginary part of a phasor is always not greater than its absolute value.
Appendix B. Proof of Equations (19)–(21)
For a filter given in Equation (15)
its frequency response at frequency is
where because is an even function. Please note that is an element of , where
Because has the form of
Then, we can obtain
The above three equations correspond to the first three elements of the first column of the identity matrix . According to Equation (A21), we have
Additionally, when , the attenuation of the estimator is very high. Thus, we can obtain
References
- IEEE Standard for Synchrophasor Measurements for Power Systems. In IEEE Std C37.118.1-2011 (Revision of IEEE Std C37.118-2005); IEEE: Piscataway, NJ, USA, 2011; pp. 1–61. [CrossRef]
- IEEE Standard for Synchrophasor Measurements for Power Systems—Amendment 1: Modification of Selected Performance Requirements. In IEEE Std C37.118.1a-2014 (Amendment to IEEE Std C37.118.1-2011); IEEE: Piscataway, NJ, USA, 2014; pp. 1–25. [CrossRef]
- Petri, D.; Fontanelli, D.; Macii, D. A Frequency-Domain Algorithm for Dynamic Synchrophasor and Frequency Estimation. IEEE Trans. Instrum. Meas. 2014, 63, 2330–2340. [Google Scholar] [CrossRef]
- Belega, D.; Fontanelli, D.; Petri, D. Dynamic Phasor and Frequency Measurements by an Improved Taylor Weighted Least Squares Algorithm. IEEE Trans. Instrum. Meas. 2015, 64, 2165–2178. [Google Scholar] [CrossRef]
- Belega, D.; Macii, D.; Petri, D. Fast Synchrophasor Estimation by Means of Frequency-Domain and Time-Domain Algorithms. IEEE Trans. Instrum. Meas. 2014, 63, 388–401. [Google Scholar] [CrossRef]
- Macii, D.; Petri, D.; Zorat, A. Accuracy Analysis and Enhancement of DFT-Based Synchrophasor Estimators in Off-Nominal Conditions. IEEE Trans. Instrum. Meas. 2012, 61, 2653–2664. [Google Scholar] [CrossRef]
- Belega, D.; Petri, D. Accuracy Analysis of the Multicycle Synchrophasor Estimator Provided by the Interpolated DFT Algorithm. IEEE Trans. Instrum. Meas. 2013, 62, 942–953. [Google Scholar] [CrossRef]
- Romano, P.; Paolone, M. Enhanced Interpolated-DFT for Synchrophasor Estimation in FPGAs: Theory, Implementation, and Validation of a PMU Prototype. IEEE Trans. Instrum. Meas. 2014, 63, 2824–2836. [Google Scholar] [CrossRef]
- Serna, J.A.D.L.O. Dynamic Phasor Estimates for Power System Oscillations. IEEE Trans. Instrum. Meas. 2007, 56, 1648–1657. [Google Scholar] [CrossRef]
- Platas-Garza, M.A.; Platas-Garza, J.; Serna, J.A.D.L.O. Dynamic Phasor and Frequency Estimates through Maximally Flat Differentiators. IEEE Trans. Instrum. Meas. 2010, 59, 1803–1811. [Google Scholar] [CrossRef]
- Mai, R.K.; He, Z.Y.; Fu, L.; Kirby, B.; Bo, Z.Q. A Dynamic Synchrophasor Estimation Algorithm for Online Application. IEEE Trans. Power Deliv. 2010, 25, 570–578. [Google Scholar] [CrossRef]
- Bi, T.; Liu, H.; Feng, Q.; Qian, C.; Liu, Y. Dynamic Phasor Model-Based Synchrophasor Estimation Algorithm for M-Class PMU. IEEE Trans. Power Deliv. 2015, 30, 1162–1171. [Google Scholar] [CrossRef]
- Ling, F.; Zhang, J.; Xiong, S.; He, Z.; Mai, R. A Modified Dynamic Synchrophasor Estimation Algorithm Considering Frequency Deviation. IEEE Trans. Smart Grid 2017, 8, 640–650. [Google Scholar]
- Serna, J.A.D.L.O.; Rodriguez-Maldonado, J. Instantaneous Oscillating Phasor Estimates With TaylorK-Kalman Filters. IEEE Trans. Power Syst. 2011, 26, 2336–2344. [Google Scholar] [CrossRef]
- Phadke, A.G.; Thorp, J.S. Synchronized Phasor Measurements and Their Applications; Springer: New York, NY, USA, 2008; pp. 121–128. [Google Scholar]
- Castello, P.; Lixia, M.; Muscas, C.; Pegoraro, P.A. Impact of the Model on the Accuracy of Synchrophasor Measurement. IEEE Trans. Instrum. Meas. 2012, 61, 2179–2188. [Google Scholar] [CrossRef]
- Serna, J.A.D.L.O.; Rodríguez-Maldonado, J. Taylor-Kalman-Fourier Filters for Instantaneous Oscillating Phasor and Harmonic Estimates. IEEE Trans. Instrum. Meas. 2012, 61, 941–951. [Google Scholar] [CrossRef]
- Platas-Garza, M.A.; Serna, J.A.D.L.O. Dynamic Harmonic Analysis Through Taylor–Fourier Transform. IEEE Trans. Instrum. Meas. 2011, 60, 804–813. [Google Scholar] [CrossRef]
- Castello, P.; Liu, J.; Muscas, C.; Pegoraro, P.A.; Ponci, F.; Monti, A. A Fast and Accurate PMU Algorithm for P + M Class Measurement of Synchrophasor and Frequency. IEEE Trans. Instrum. Meas. 2014, 63, 2837–2845. [Google Scholar] [CrossRef]
- Platas-Garza, M.A.; Serna, J.A.D.L.O. Polynomial Implementation of the Taylor–Fourier Transform for Harmonic Analysis. IEEE Trans. Instrum. Meas. 2014, 63, 2846–2854. [Google Scholar] [CrossRef]
- Serna, J.A.D.L.O. Synchrophasor Measurement With Polynomial Phase-Locked-Loop Taylor-Fourier Filters. IEEE Trans. Instrum. Meas. 2015, 64, 328–337. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Yu, Y.; Wang, Q.; Huang, S. Improved Interpolated Dynamic DFT Synchrophasor Estimator Considering Second Harmonic Interferences. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference, Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar]
- Wang, F.; Zhao, W.; Guo, L.; Wang, C.; Jiang, X.; Wang, Z. Optimal filter design for frequency and synchrophasor measurement. Proc. CSEE 2017, 37, 6691–6699. [Google Scholar]
- Alomar, A.M.A.; Shamseldin, B.E.M. Alternative Approaches for Distinguishing between Faults and Inrush Current in Power Transformers. Energy Power Eng. 2014, 6, 143–160. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).