Localization and Discrimination of the Perturbation Signals in Fiber Distributed Acoustic Sensing Systems Using Spatial Average Kurtosis
Abstract
:1. Introduction
2. Methods
2.1. Kurtosis of Acoustic Signals in Phase-Sensitive Optical Time-Domain Reflectometry
- (1)
- Random noise. In Φ-OTDR systems, noises are mainly caused by phase noise of the laser, partial interferometric problem, and electrical noises such as thermal noise and shot noise [5]. These noises nearly follow a normal distribution, thus their kurtosis should be around 0. A Gaussian white noise with the amplitude of 2 mV is used to simulate the random noise in Φ-OTDR systems, shown in Figure 1a. Its kurtosis is 0.09.
- (2)
- Instantaneous destructive perturbations. These signals (structural cracks, gas explodes, excavation damage, destructive intrusions, etc.) are virtually short-time and non-stationary, whose frequency distribution change rapidly over time. They generally have certain extreme values, thus their kurtosis should be positive. Transient signal in Figure 1b is used to simulate the instantaneous destructive perturbations, which is generated by a 5–400 Hz broadband damped sinusoidal signal plus a Gaussian white noise with the amplitude of 1 mV, and the kurtosis of it is 6.25.
- (3)
- Environmental interferences. These signals (wind, the vehicle engine, structural free vibration, etc.) are mostly continuous and stationary, whose frequency distribution is fixed in a short time period. They usually have no extreme values, thus their kurtosis should be negative. Signals in Figure 1c–f are used to simulate environmental interferences. Signals in Figure 1c,d are simulated by a sinusoidal signal with the amplitude of 1 mV plus a Gaussian white noise with the amplitude of 1 mV, which are used to simulate the natural vibrations of the structures. Their sinusoidal signal frequencies are 5 Hz and 200 Hz and their kurtosis are −1.14 and −1.01 respectively. Signals in Figure 1e,f are band-limited white noises, which are used to simulate the environmental interferences such as wind. Their frequency band are 5–15 Hz and 45–65 Hz and their kurtosis are −1.10 and −1.01, respectively.
2.2. Spatial Kurtosis of Rayleigh Optical Time-Domain Reflectometry Traces
2.3. Moving Average on the Spatial Dimension
3. Experimental Results
3.1. Experimental Setup
3.2. Localization Results of Instantaneous Destructive Perturbations
3.2.1. Signal-to-Noise Ratio Improvement of the Locating Information
3.2.2. Locating Accuracy
3.2.3. Time Consumption
3.3. Discrimination of Perturbations
4. Discussion
- (1)
- It can locate the instantaneous destructive perturbations with a higher SNR. This is because that the Φ-OTDR signals caused by instantaneous destructive perturbations generally have extreme value and result in large positive kurtosis, while noises in Φ-OTDR basically obey normal distribution and result in zero-kurtosis.
- (2)
- It has better locating accuracy. By using a moving average on the spatial dimension, the SAK method can accurately locate the center of the vibration segment, even if the subsection is in an insensitive state, thus leading to more accurate locating results. It should be noted that “moving average on the spatial dimension” can be also used in other locating methods to fast figure out the accurate vibration segment center.
- (3)
- It can simultaneously locate the perturbations and to some degree evaluate whether they are destructive or just interference. Because instantaneous destructive perturbations generally have higher positive kurtosis, while stationary interferences usually have lower negative kurtosis. The pencil-break, digging, and PZT discrimination results show that the SAK might be a promising feature for further event recognition.
- (4)
- The time consumption of SAK method is short enough for a long distance real-time Φ-OTDR system. It should be noted that here the time consumption include both the locating time and discriminating time.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Juarez, J.C.; Taylor, H.F. Distributed fiber optic intrusion sensor system. J. Light. Technol. 2005, 23, 2081–2087. [Google Scholar] [CrossRef]
- Juarez, J.C.; Taylor, H.F. Field test of a distributed fiber-optic intrusion sensor system for long perimeters. Appl. Opt. 2007, 46, 1968–1971. [Google Scholar] [CrossRef] [PubMed]
- Martins, H.F.; Martin-Lopez, S.; Corredera, P.; Filograno, M.L.; Frazão, O.; González-Herráez, M. High visibility phase-sensitive optical time domain reflectometer for distributed sensing of ultrasonic waves. Proc. SPIE 2013, 8794, 87943F-1–87943F-4. [Google Scholar] [CrossRef]
- Peng, F.; Wu, H.; Jia, X.H.; Rao, Y.J.; Wang, Z.N.; Peng, Z.P. Ultra-long high-sensitivity Φ-OTDR for high spatial resolution intrusion detection of pipelines. Opt. Express 2014, 22, 13804–13810. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Zhu, T.; Chen, L.; Bao, X. Distributed vibration sensor based on coherent detection of phase-OTDR. J. Light. Technol. 2010, 28, 3243–3249. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, L.; Bao, X. Wavelet denoising method for improving detection performance of distributed vibration sensor. IEEE Photon. Technol. Lett. 2012, 24, 542–544. [Google Scholar] [CrossRef]
- Yi, S.; Hao, F.; Zhoumo, Z. A long distance phase-sensitive optical time domain reflectometer with simple structure and high locating accuracy. Sensors 2015, 15, 21957–21970. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, H.; Chang, J. Signal-to-noise ratio enhancement based on empirical mode decomposition in phase-sensitive optical time domain reflectometry systems. Sensors 2017, 17, 1870. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, H.; Chang, J. Detection performance improvement of distributed vibration sensor based on curvelet denoising method. Sensors 2017, 17, 1380. [Google Scholar] [CrossRef]
- Ölçer, İ.; Öncü, A. Adaptive temporal matched filtering for noise suppression in fiber optic distributed acoustic sensing. Sensors 2017, 17, 1288. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.; Xiao, X.; He, Q.; Diao, D. Enhancement of SNR and spatial resolution in Φ-OTDR system by using two-dimensional edge detection method. J. Light. Technol. 2013, 31, 2851–2856. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, B.; Wang, Y.; Wang, D.; Liu, X.; Bai, Q. Real-time distributed vibration monitoring system using Φ-OTDR. IEEE Sens. J. 2017, 17, 1333–1341. [Google Scholar] [CrossRef]
- He, H.; Shao, L.; Li, H.; Pan, W.; Luo, B.; Zou, X.; Yan, L. SNR enhancement in phase-sensitive OTDR with adaptive 2-D bilateral filtering algorithm. IEEE Photon. J. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, L.; Bao, X. Continuous wavelet transform for non-stationary vibration detection with phase-OTDR. Opt. Express 2012, 20, 20459–20465. [Google Scholar] [CrossRef] [PubMed]
- Hui, X.; Ye, T.; Zheng, S.; Zhou, J.; Chi, H.; Jin, X.; Zhang, X. Space-frequency analysis with parallel computing in a phase-sensitive optical time-domain reflectometer distributed sensor. Appl. Opt. 2014, 53, 6586–6590. [Google Scholar] [CrossRef] [PubMed]
- Yue, H.; Wu, Y.; Zhao, B.; Ou, Z. Simultaneous and signal-to-noise ratio enhancement extraction of vibration location and frequency information in phase-sensitive optical time domain reflectometry distributed sensing system. Opt. Eng. 2015, 54, 047101:1–047101:6. [Google Scholar] [CrossRef]
- Shi, Y.; Feng, H.; Huang, Y.; Zeng, Z. Correlation dimension locating method for phase-sensitive optical time domain reflectometry. Opt. Eng. 2016, 55, 091402:1–091402:5. [Google Scholar] [CrossRef]
- Wu, H.; Xiao, S.; Li, X.; Wang, Z.; Xu, J.; Rao, Y. Separation and determination of the disturbing signals in phase-sensitive optical time domain reflectometry (Φ-OTDR). J. Light. Technol. 2015, 33, 3156–3162. [Google Scholar] [CrossRef]
- Sun, Q.; Feng, H.; Yan, X.; Zeng, Z. Recognition of a phase-sensitivity OTDR sensing system based on morphologic feature extraction. Sensors 2015, 15, 15179–15197. [Google Scholar] [CrossRef] [PubMed]
- Tejedor, J.; Martins, H.F.; Piote, D.; Macias-Guarasa, J.; Pastor-Graells, J.; Martin-Lopez, S.; Guillén, P.C.; Smet, F.D.; Postvoll, W.; González-Herráez, M. Toward prevention of pipeline integrity threats using a smart fiber-optic surveillance system. J. Light. Technol. 2016, 34, 4445–4453. [Google Scholar] [CrossRef]
- Tejedor, J.; Macias-Guarasa, J.; Martins, H.; Piote, D.; Pastor-Graells, J.; Martin-Lopez, S.; Corredera, P.; Gonzalez-Herraez, M. A novel fiber optic based surveillance system for prevention of pipeline integrity threats. Sensors 2017, 17, 355. [Google Scholar] [CrossRef] [PubMed]
- Jiang, F.; Li, H.; Zhang, Z.; Zhang, X. An event recognition method for fiber distributed acoustic sensing systems based on the combination of MFCC and CNN. Proc. SPIE 2017, 10618, 1061804-1–1061804-7. [Google Scholar] [CrossRef]
- Izumita, H.; Furukawa, S.I.; Koyamada, Y.; Sankawa, I. Fading noise reduction in coherent OTDR. IEEE Photon. Technol. Lett. 1992, 4, 201–203. [Google Scholar] [CrossRef]



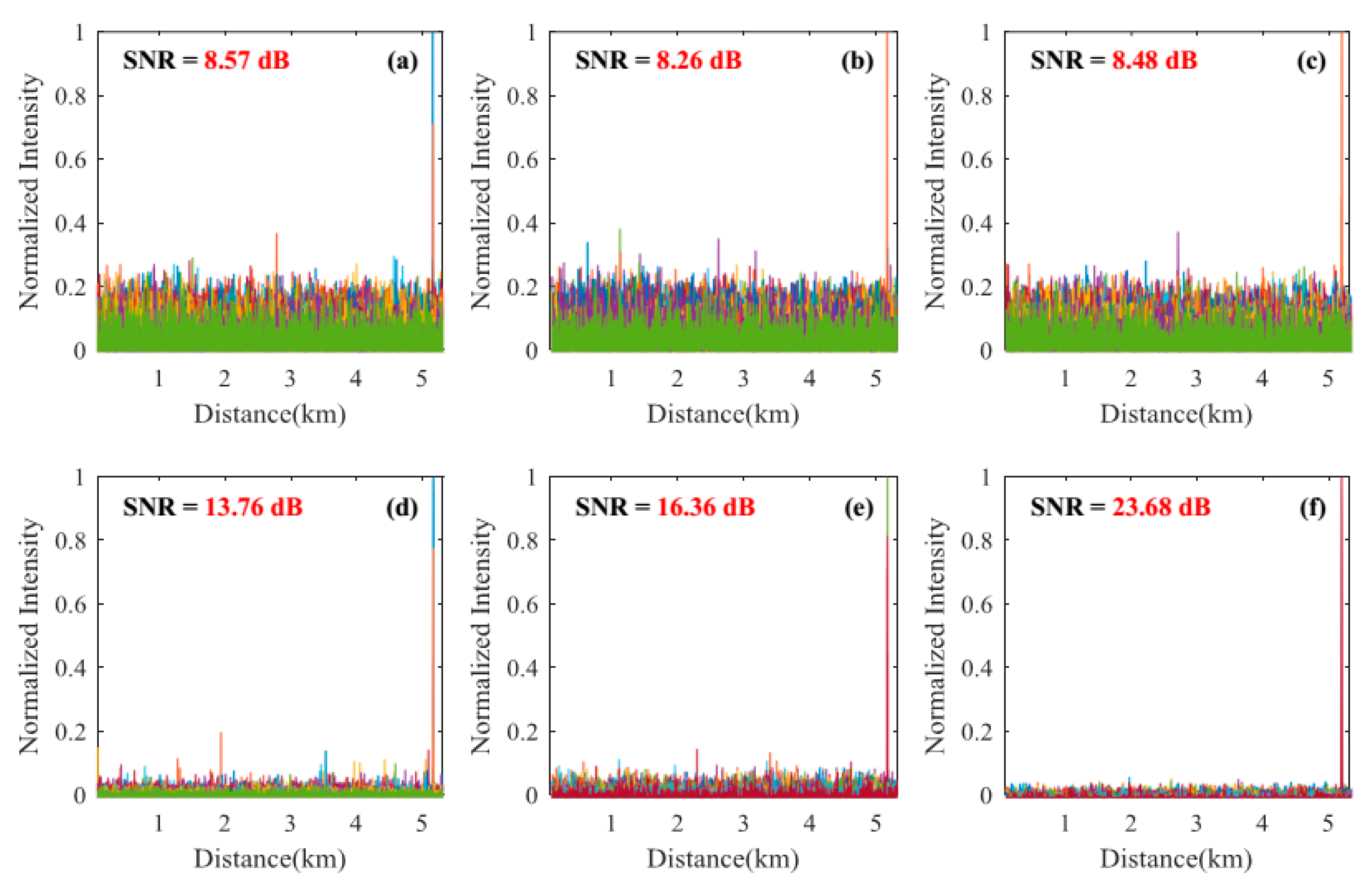








| Event | Pulse Width | MAD | TED | WD | MWD | SK | SAK |
|---|---|---|---|---|---|---|---|
| Pencil-break (dB) | 100 ns | 9.14 | 10.07 | 14.72 | 9.75 | 19.79 | 24.87 |
| 500 ns | 5.12 | 5.03 | 6.86 | 5.39 | 14.82 | 22.20 | |
| Digging (dB) | 100 ns | 8.70 | 11.57 | 14.31 | 11.18 | 16.22 | 22.04 |
| 500 ns | 4.56 | 6.42 | 8.93 | 6.12 | 15.72 | 23.81 |
| Event | Pulse Width | Statistics | MAD | TED | WD | MWD | SK | SAK |
|---|---|---|---|---|---|---|---|---|
| Pencil-break (m) | 100 ns | Avg. | 5163.9 | 5164.2 | 5164.3 | 5164.3 | 5163.6 | 5163.4 |
| Std. | 1.7 | 1.9 | 1.7 | 1.6 | 2.3 | 0.8 | ||
| 500 ns | Avg. | 5165.8 | 5163.7 | 5164.6 | 5162.9 | 5162.4 | 5165.4 | |
| Std. | 9.6 | 8.6 | 9.9 | 8.7 | 10.3 | 1.9 | ||
| Digging (m) | 100 ns | Avg. | 5219.7 | 5219.5 | 5219.3 | 5220.0 | 5218.5 | 5219.9 |
| Std. | 1.3 | 1.2 | 1.1 | 2.0 | 2.1 | 0.7 | ||
| 500 ns | Avg. | 5220.4 | 5221.9 | 5221.3 | 5221.2 | 5219.0 | 5221.5 | |
| Std. | 11.6 | 11.0 | 10.9 | 10.3 | 11.6 | 1.2 |
| Events | Fold Index | TPR | FPR | Acc. |
|---|---|---|---|---|
| Pencil-Break or Digging | 1 | 94.12% | 1.23% | 96.64% |
| 2 | 97.26% | 1.32% | 97.99% | |
| 3 | 95.65% | 0.00% | 97.99% | |
| 4 | 95.24% | 1.54% | 96.64% | |
| Avg. | 95.57% | 1.02% | 97.32% | |
| PZT Vibration | 1 | 93.15% | 6.58% | 93.29% |
| 2 | 90.41% | 1.32% | 94.63% | |
| 3 | 94.20% | 2.50% | 95.97% | |
| 4 | 92.41% | 7.14% | 92.62% | |
| Avg. | 92.54% | 4.38% | 94.13% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, F.; Li, H.; Zhang, Z.; Zhang, Y.; Zhang, X. Localization and Discrimination of the Perturbation Signals in Fiber Distributed Acoustic Sensing Systems Using Spatial Average Kurtosis. Sensors 2018, 18, 2839. https://doi.org/10.3390/s18092839
Jiang F, Li H, Zhang Z, Zhang Y, Zhang X. Localization and Discrimination of the Perturbation Signals in Fiber Distributed Acoustic Sensing Systems Using Spatial Average Kurtosis. Sensors. 2018; 18(9):2839. https://doi.org/10.3390/s18092839
Chicago/Turabian StyleJiang, Fei, Honglang Li, Zhenhai Zhang, Yixin Zhang, and Xuping Zhang. 2018. "Localization and Discrimination of the Perturbation Signals in Fiber Distributed Acoustic Sensing Systems Using Spatial Average Kurtosis" Sensors 18, no. 9: 2839. https://doi.org/10.3390/s18092839
APA StyleJiang, F., Li, H., Zhang, Z., Zhang, Y., & Zhang, X. (2018). Localization and Discrimination of the Perturbation Signals in Fiber Distributed Acoustic Sensing Systems Using Spatial Average Kurtosis. Sensors, 18(9), 2839. https://doi.org/10.3390/s18092839





