A High-Efficiency Data Collection Method Based on Maximum Recharging Benefit in Sensor Networks
Abstract
:1. Introduction
2. Related Works
2.1. Mobile Data Collection and Energy Replenishment in WRSN
- Random Mobility: The movement of MDC is on a random trajectory.
- Fixed Mobility: The MDC moves along a fixed pre-specified path.
- Controlled Mobility: The trajectory of MDC is controlled depending on its position and the density of data in its vicinity.
2.2. Path Planning about the Wireless Charging Vehicle
3. Network Model
3.1. Network Architecture
- (1)
- How to get the minimum number of MDCs and how to design a reasonable and feasible data collection scheme under the constraint of network size, number of nodes as well as time delay to achieve real-time and efficient data collection with balanced energy consumption;
- (2)
- How to properly divide the network into regions based on the minimum number of MDCs;
- (3)
- How to set a reasonable recharging threshold for each node and formulate an optimal recharging scheme under the condition of limited battery capacity of WCV, so as to recharge the requested nodes in time and maximize the recharging efficiency.
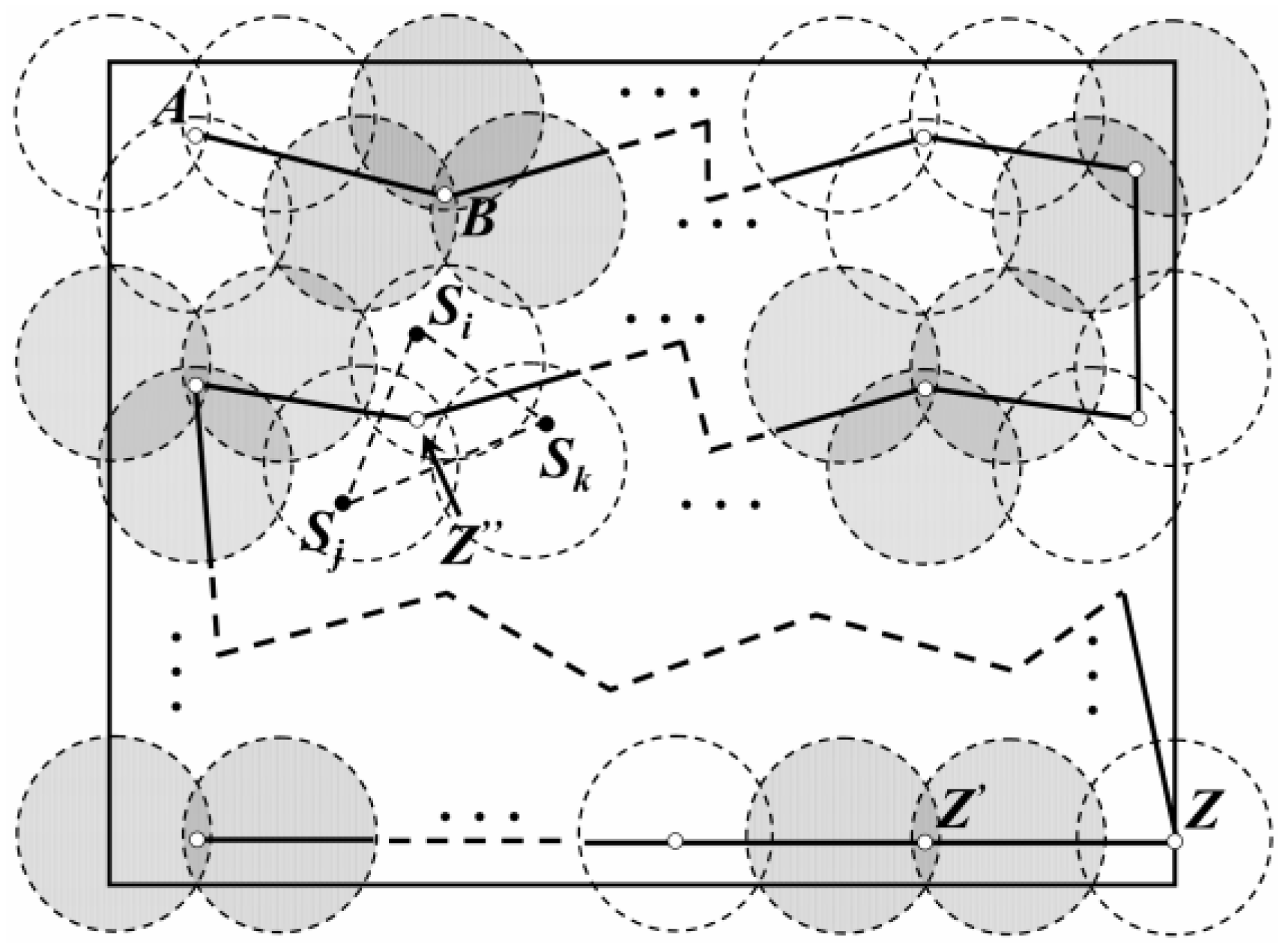
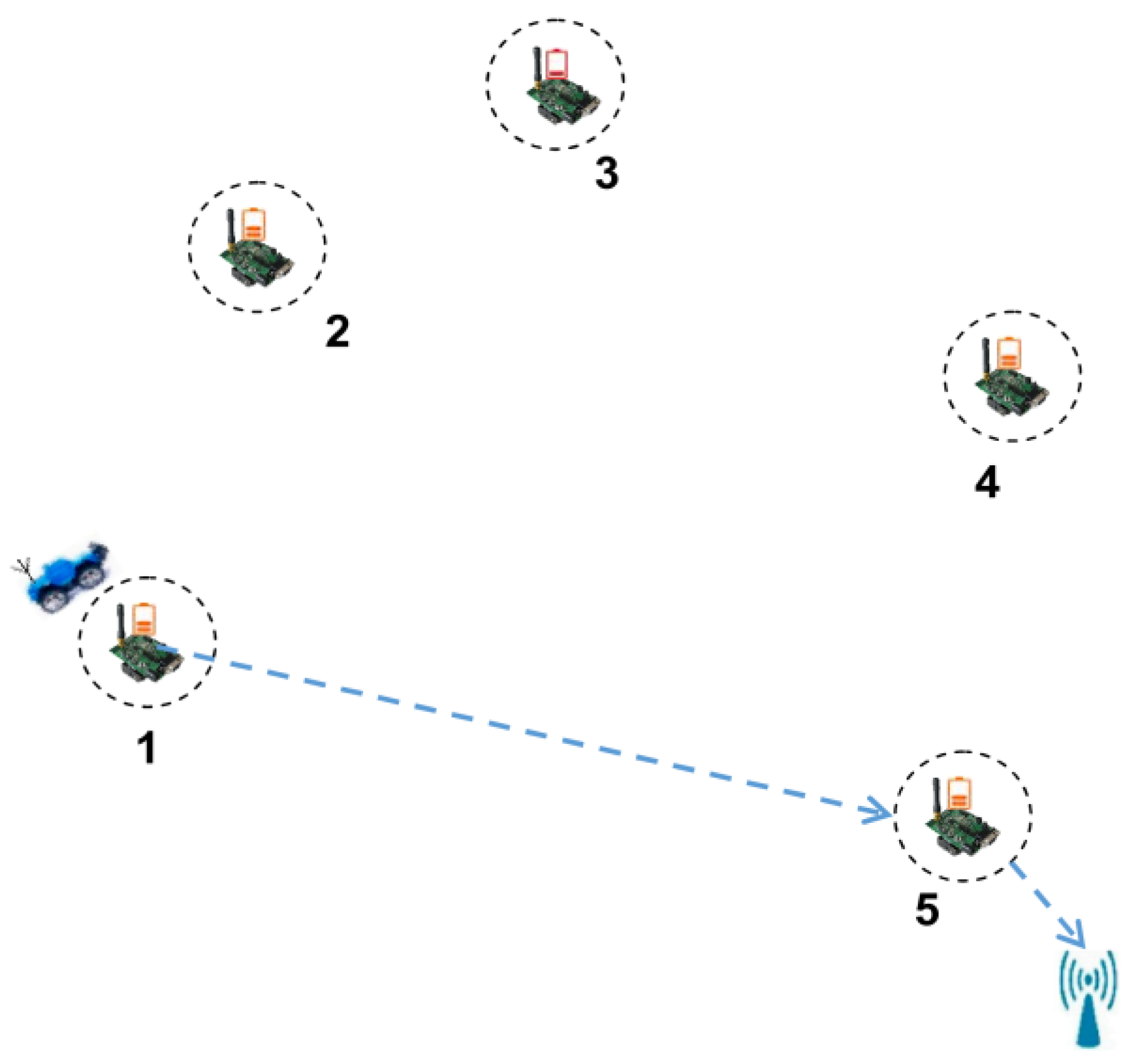
3.2. Virtual Traverse Points
- (1)
- When the MDC arrives at the VTP, it can only receive data uploaded by nodes located in its communication region.
- (2)
- Each sensor node in the network should have the opportunity to upload data to the MDC within one hop.
- (3)
- In order to avoid repeated collection of redundant data and to enhance the real-time performance, MDCs are only allowed to pass through each VTP once and only once during a round of data gathering time.
4. Multi-MDCs Based Data Collection Strategy with Maximum Delay Constraint
4.1. The Minimum Number of MDCs that Meets the Delay Constraint
- (1)
- Data collected from any node in the network must be transmitted to BS within the time period, Td. In other words, the constraint of the maximum time delay needs to be met.
- (2)
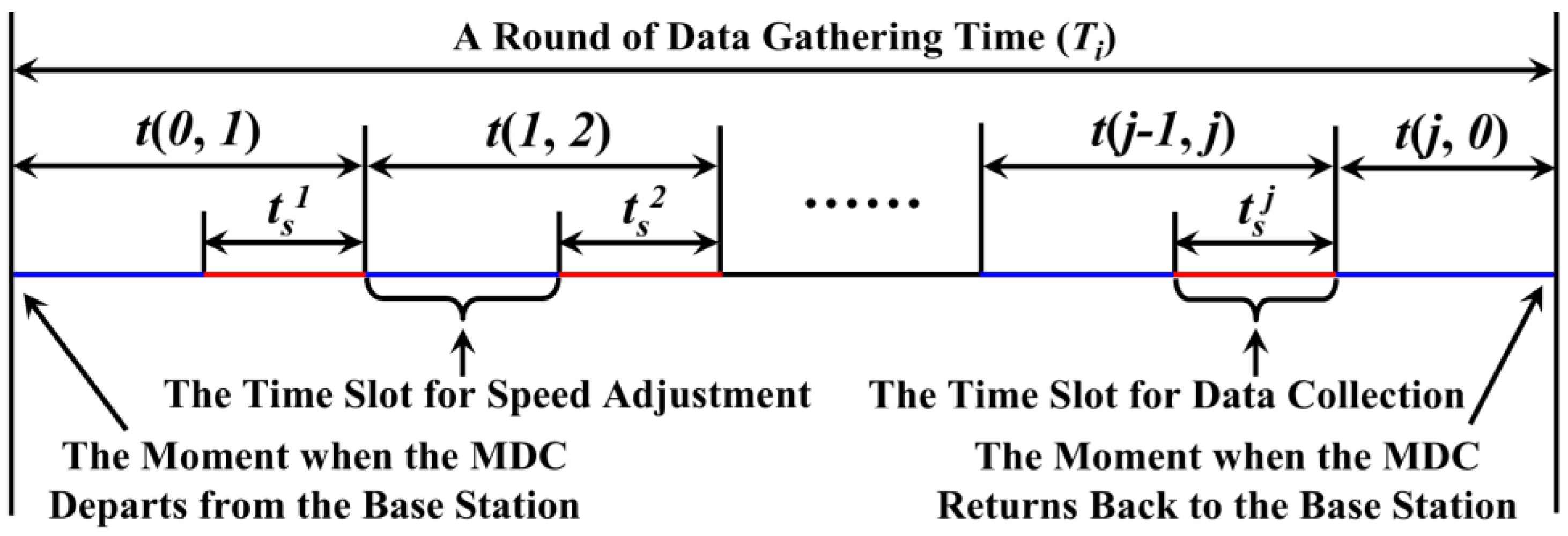
- Each VTP needs to be accessed by one MDC only once during the time period, Tr.
- (3)
- During each round of data collection, the MDC needs to depart from BS and eventually return to BS.
- (4)
- The MDC can only stay at the BS or the VTPs. Moreover, the regular hexagons where the MDC stays at for two consecutive times must be adjacent.
- (5)
- The MDC moves linearly between two consecutive VTPs, and its speed is vMDC.
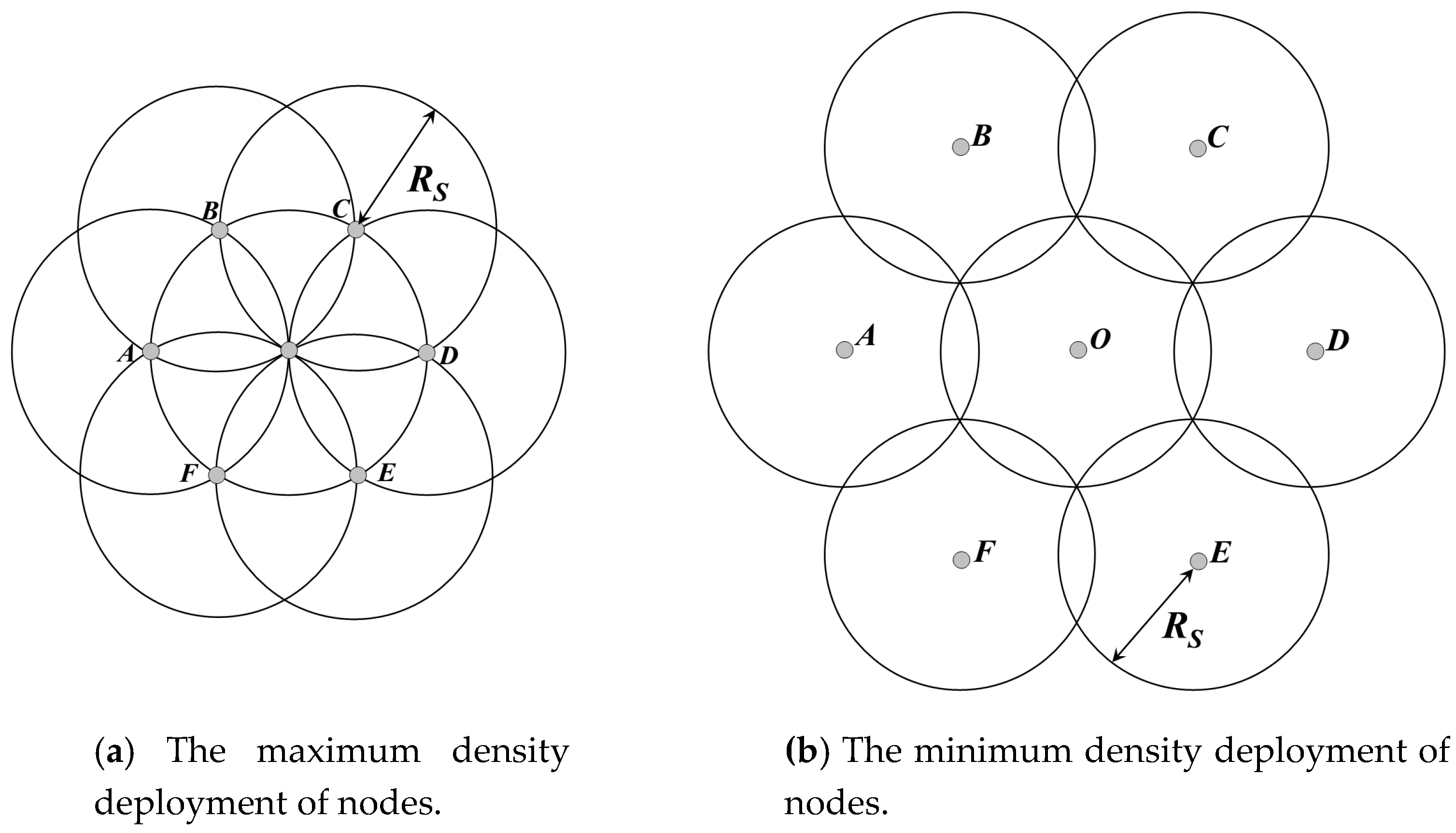
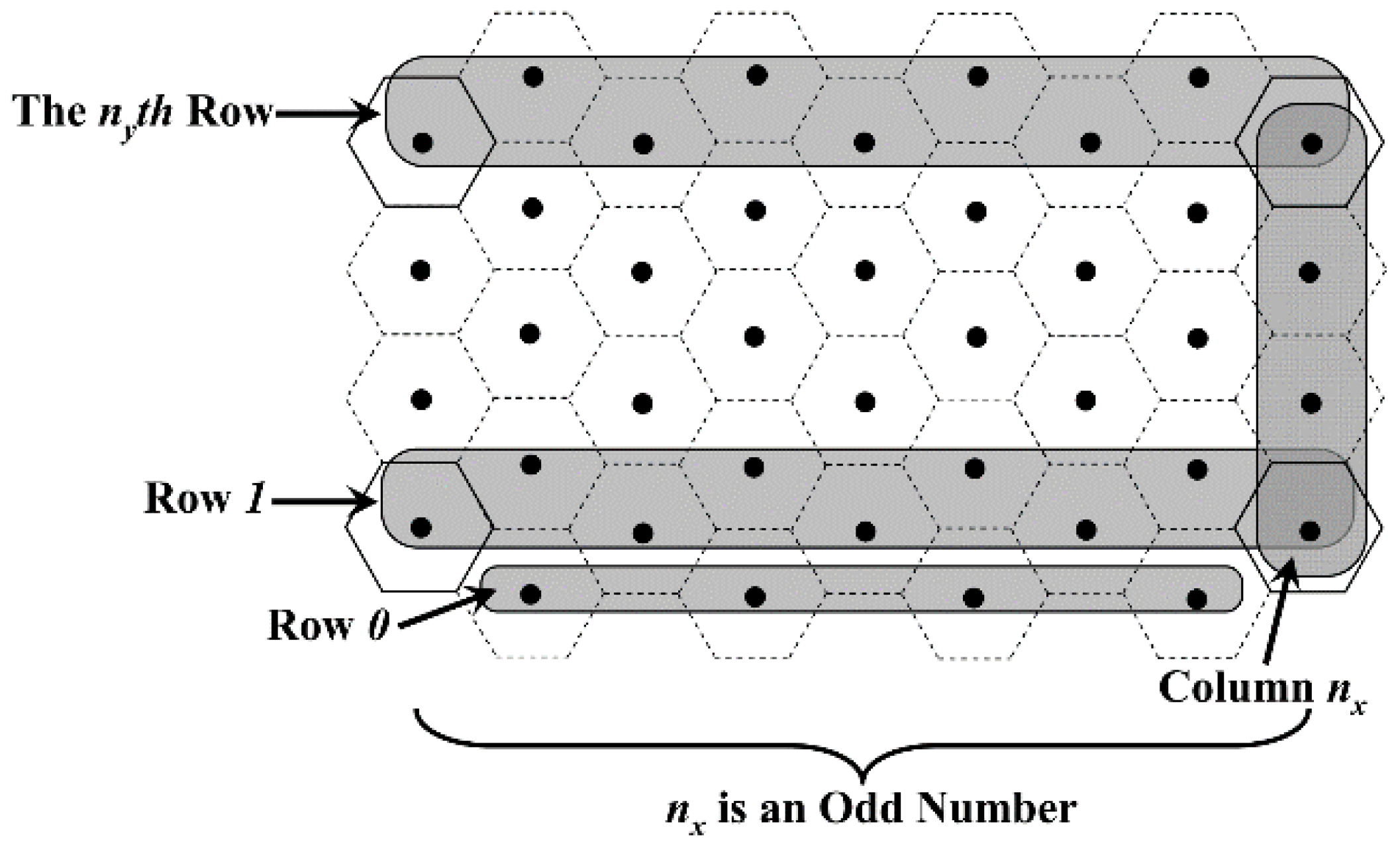
4.2. Network Partition Method Based on Virtual Scan Line
4.3. Region Size Adjustment
4.4. Speed Adjustment Scheme for Ensuring Data Integrity
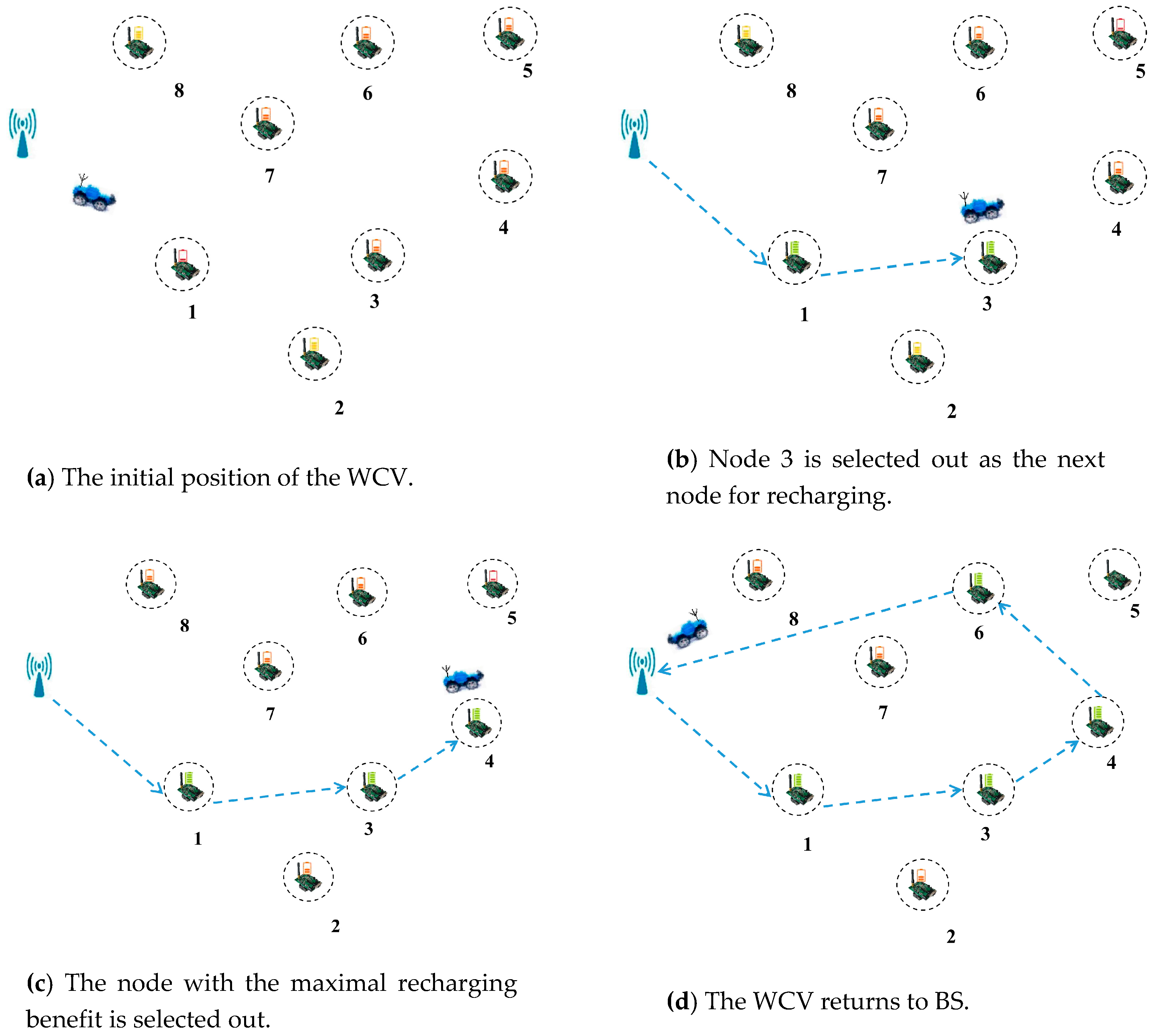
5. An Adaptive Recharging Scheme Based on Maximum Benefit
5.1. Energy Threshold of the Recharging Request
5.2. Wireless Recharging Scheme Based on Limited Battery Capacity and the Maximum Recharging Benefit
6. Simulation Results and Analysis
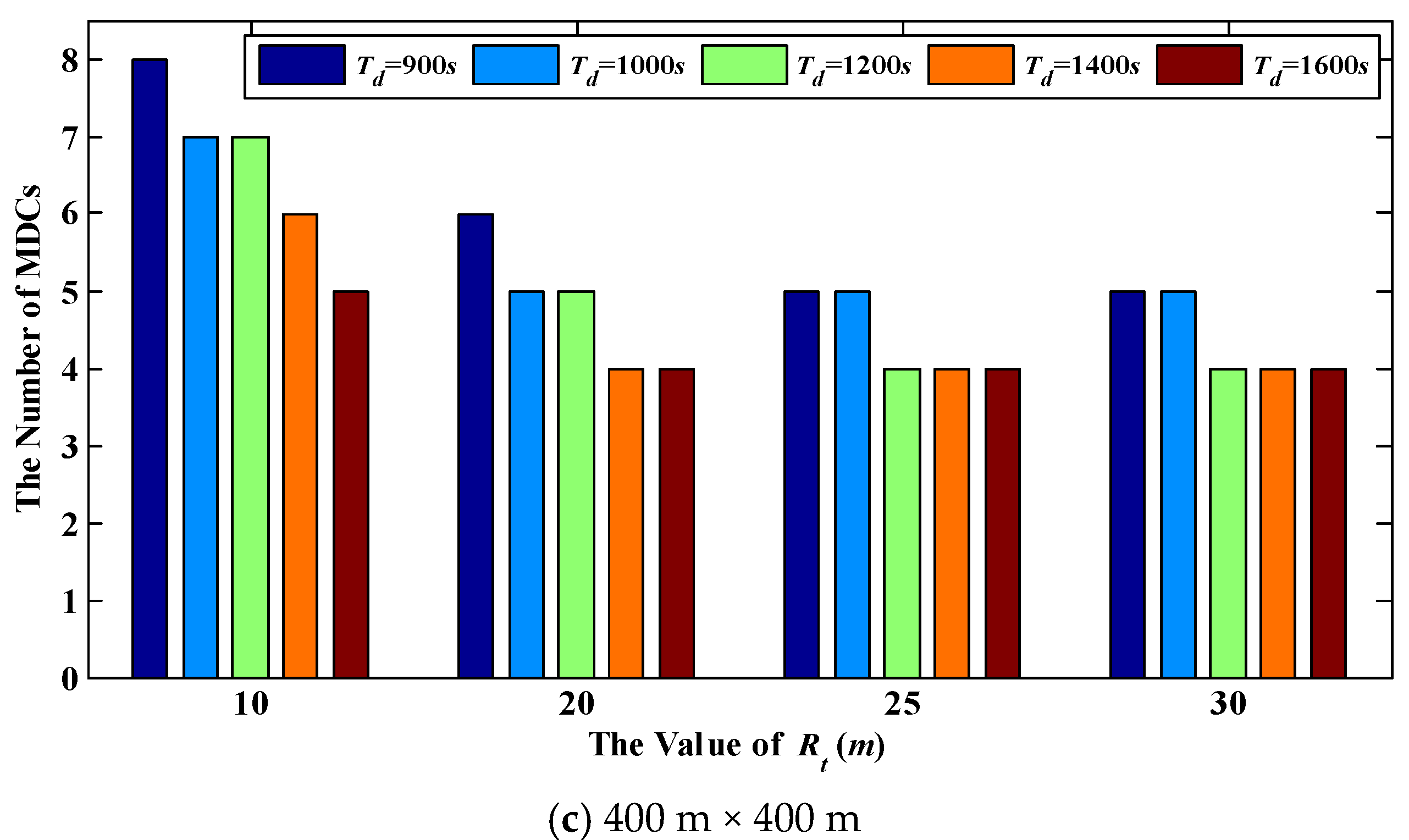
6.1. The Minimum Number of MDCs
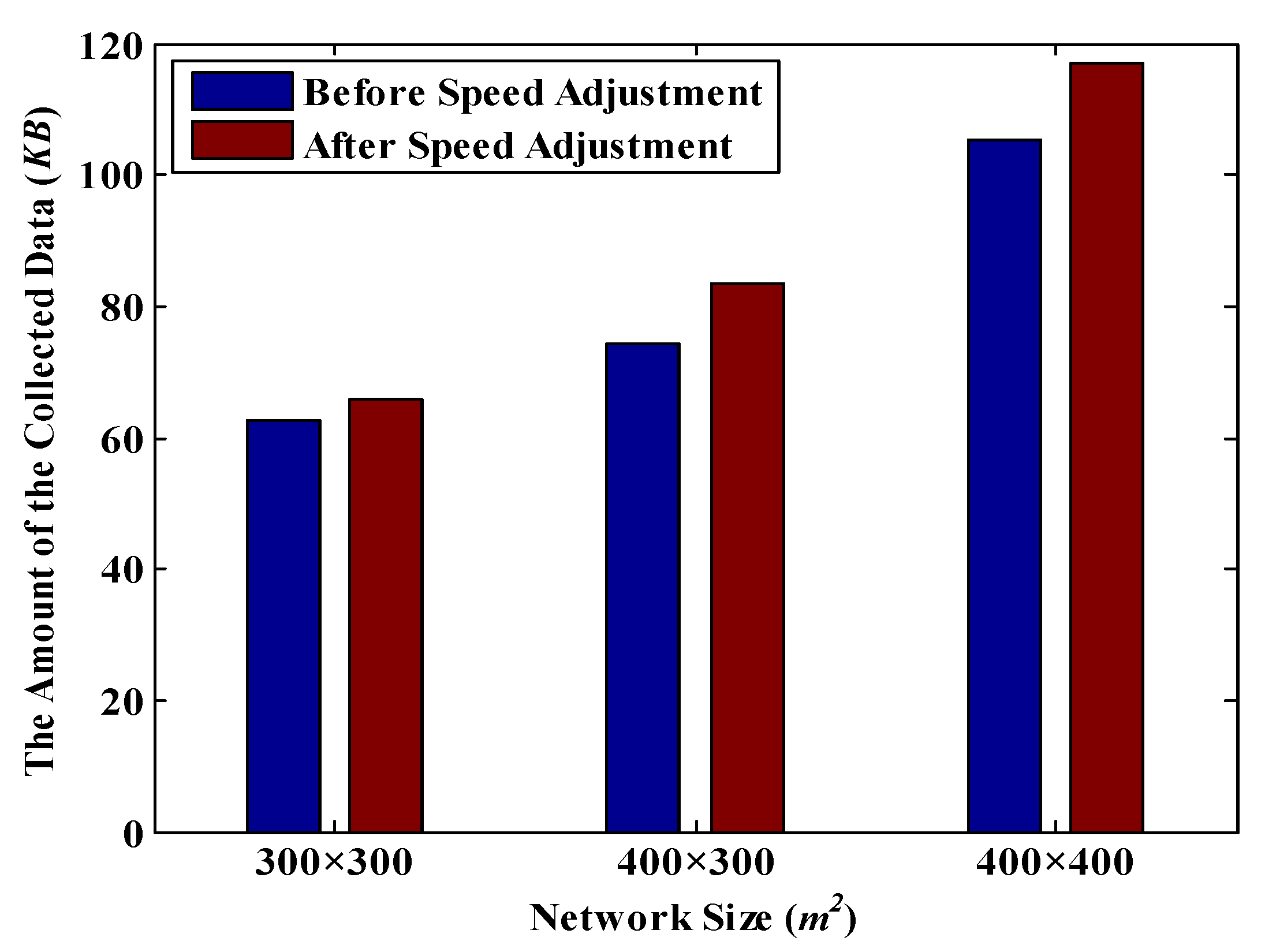
6.2. The Amount of Data Collected before and after Speed Adjustment
6.3. Effect of Recharging Rate on the Performance of WRSN
- The Proportion of the Dead Nodes (PDN): The ratio of the number of dead nodes to the total number of nodes deployed in the network.
- The Average Recharging Delay (ARD): The average time interval from the moment when a node sending a recharging request to the moment when it being recharged.
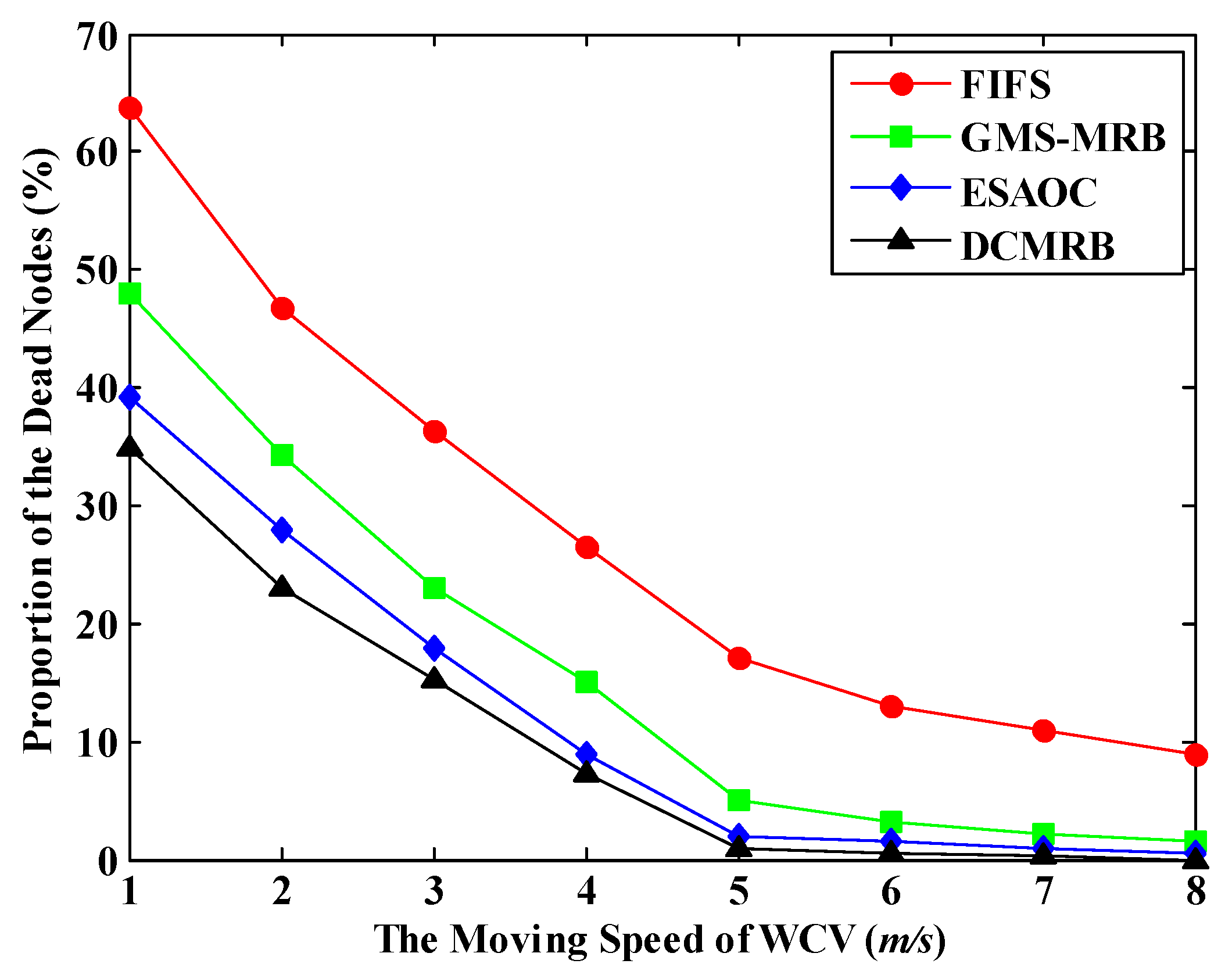
6.4. Effect of the Moving Speed of WCV on the Performance of WRSN
6.5. Effect of the Threshold of Recharging Request on the Performance of WRSN
6.6. Effect of the Recharging Rate on the Amount of the Collected Data
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, H.; Tong, X.J.; Wang, Z. Research on relay node placement considering load balancing based on greedy optimization algorithm in wireless sensor networks. Comput. Sci. 2015, 6, 115–119. [Google Scholar]
- Liu, L.F.; Guo, P.; Zhao, J.; Li, N. Data collection strategy based on improved LEACH protocol. Comput. Sci. 2015, 6, 299–302. [Google Scholar]
- Zhang, M.Y.; Cai, W.Y.; Zhou, L.P.; EE Department. Clustered predictive model based adaptive sampling techniques in wireless sensor networks. J. Electron. Inf. Technol. 2015, 1, 200–205. [Google Scholar]
- Mammu, A.S.K.; Hernandez-Jayo, U.; Sainz, N.; de la Iglesia, I. Cross-layer cluster-based energy- efficient protocol for wireless sensor networks. Sensors 2015, 15, 8314–8336. [Google Scholar] [CrossRef] [PubMed]
- Abba, S.; Lee, J.-A. An autonomous self-aware and adaptive fault tolerant routing technique for wireless sensor networks. Sensors 2015, 15, 20316–20354. [Google Scholar] [CrossRef] [PubMed]
- Xie, R.N.; Liu, A.F.; Gao, J.L. A Residual energy aware schedule scheme for WSNs employing adjustable awake/sleep duty cycle. Wirel. Pers. Commun. 2016, 4, 1–29. [Google Scholar] [CrossRef]
- Mohammed, A.-Z.; Sabah, M.A.; Nabil, S.; Shigenobu, S. Mobile Sink-Based Adaptive Immune Energy-Efficient Clustering Protocol for Improving the Lifetime and Stability Period of Wireless Sensor Networks. IEEE Sens. J. 2015, 8, 4576–4586. [Google Scholar]
- Mario, D.F.; Sajal, K.D.; Giuseppe, A. Data collection in wireless sensor networks with mobile elements: A survey. ACM Trans. Sens. Netw. (TOSN) 2011, 1, 1–31. [Google Scholar]
- Ryo, S.; Rajesh, K.G. Optimal Speed Control of Mobile Node for Data Collection in Sensor Networks. IEEE Trans. Mob. Comput. 2009, 1, 127–139. [Google Scholar]
- Zhao, M.; Yang, Y.Y. Optimization-Based Distributed Algorithms for Mobile Data Gathering in Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2012, 10, 1464–1477. [Google Scholar] [CrossRef]
- Guo, S.T.; Wang, C.; Yang, Y.Y. Joint mobile data gathering and energy provisioning in wireless rechargeable sensor networks. IEEE Trans. Mob. Comput. 2014, 12, 2836–2852. [Google Scholar] [CrossRef]
- Zhong, P.; Zhang, Y.; Ma, S.; Kui, X.; Gao, J. RCSS: A real-time on-demand charging scheduling scheme for wireless rechargeable sensor networks. Sensors 2018, 18, 1601. [Google Scholar] [CrossRef] [PubMed]
- Vijayakumar, S.C.; Karthikeyan, M.; Jeninprabu, R. Solar powered bicycle for WSN control and remote power management applications. Int. J. Appl. Eng. Res. 2015, 4, 11103–11111. [Google Scholar]
- Wang, C.; Li, J.; Yang, Y.Y.; Ye, F. Combining solar energy harvesting with wireless charging for hybrid wireless sensor networks. IEEE Trans. Mob. Comput. 2018, 3, 560–576. [Google Scholar] [CrossRef]
- Ren, X.J.; Liang, W.F. Delay-tolerant data gathering in energy harvesting sensor networks with a mobile sink. In Proceedings of the IEEE Global Communication Conference, Anaheim, CA, USA, 3–7 December 2012. [Google Scholar]
- Tang, L.; Cai, J.; Yan, J.; Zhou, Z. Joint energy supply and routing path selection for rechargeable wireless sensor networks. Sensors 2018, 18, 1962. [Google Scholar] [CrossRef] [PubMed]
- Rao, X.P.; Yang, P.L.; Yan, Y.B.; Zhou, H.; Wu, X.G. Optimal recharging with practical considerations in wireless rechargeable sensor network. IEEE Access 2017, 5, 4401–4409. [Google Scholar] [CrossRef]
- Wang, C.; Li, J.; Ye, F.; Yang, Y.Y. A mobile data gathering framework for wireless rechargeable sensor networks with vehicle movement costs and capacity constraints. IEEE Trans. Comput. 2016, 8, 2411–2427. [Google Scholar] [CrossRef]
- Peng, Y.; Li, Z.; Wang, Z.; Zhang, W.S.; Qiao, D.J. Prolonging sensor network lifetime through wireless charging. In Proceedings of the 2010 31st IEEE Real-Time Systems Symposium, San Diego, CA, USA, 30 November–3 December 2010. [Google Scholar]
- Mehrabi, A.; Kim, K. Maximizing Data Collection Throughput on a Path in Energy Harvesting Sensor Networks Using a Mobile Sink. IEEE Trans. Mob. Comput. 2016, 3, 690–704. [Google Scholar] [CrossRef]
- Konstantopoulos, C.; Pantziou, G.; Gavalas, D.; Mpitziopoulos, A.; Mamalis, B. A rendezvous-based approach enabling energy-efficient sensory data collection with mobile sinks. IEEE Trans. Parallel Distrib. Syst. 2012, 5, 809–817. [Google Scholar] [CrossRef]
- de Freitas, E.P.; Heimfarth, T.; Vinel, A.; Wagner, F.R.; Pereira, C.E.; Larsson, T. Cooperation among wirelessly connected static and mobile sensor nodes for surveillance applications. Sensors 2013, 13, 12903–12928. [Google Scholar] [CrossRef] [PubMed]
- Sha, C.; Qiu, J.M.; Li, S.Y.; Qiang, M.Y.; Wang, R.C. A type of energy-efficient data gathering method based on single sink moving along fixed points. Peer-to-Peer Netw. Appl. 2018, 3, 361–379. [Google Scholar] [CrossRef]
- Sha, C.; Qiu, J.M.; Lu, T.Y.; Wang, T.T.; Wang, R.C. Virtual region based data gathering method with mobile sink for sensor networks. Wirel. Netw. 2018, 5, 1793–1807. [Google Scholar] [CrossRef]
- Sha, C.; Qiu, J.M.; Li, S.Y.; Qiang, M.Y.; Wang, R.C. A type of low-latency data gathering method with multi-sink for sensor networks. Sensors 2016, 16, 923. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Zhang, H.K.; Das, S.K. Efficient data vollection in wireless sensor networks with path-constrained mobile sinks. IEEE Trans. Mob. Comput. 2011, 4, 592–608. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, H.K. Optimal path selection for mobile sink in delay-guaranteed sensor networks. Acta Electron. Sin. 2011, 4, 742–747. [Google Scholar]
- Gu, Y.Y.; Bozdag, D.; Ekici, E.; Ozguner, F.; Lee, C.-G. Partitioning based mobile element scheduling in Wireless Sensor Networks. In Proceedings of the Second Annual IEEE Conference on Sensor and Ad Hoc Communications and Networks, SECON, Santa Clara, CA, USA, 26–29 September 2005. [Google Scholar]
- Zhao, M.; Li, J.; Yang, Y.Y. A framework of joint mobile energy replenishment and data gathering in wireless rechargeable sensor networks. IEEE Trans. Mob. Comput. 2014, 12, 2689–2705. [Google Scholar] [CrossRef]
- Dasgupta, R.; Yoon, S. Energy-efficient deadline-aware data-gathering scheme using multiple mobile data collectors. Sensors 2017, 17, 742. [Google Scholar] [CrossRef] [PubMed]
- Zhong, P.; Li, Y.T.; Liu, W.R.; Duan, G.H.; Chen, Y.W.; Xiong, N. Joint mobile data collection and wireless energy transfer in wireless rechargeable sensor networks. Sensors 2017, 17, 1881. [Google Scholar] [CrossRef] [PubMed]
- Majid, I.K.; Wilfried, N.G.; Guenter, H. Static vs. mobile sink: The influence of basic parameters on energy efficiency in wireless sensor networks. Comput. Commun. 2013, 9, 965–978. [Google Scholar]
- Shi, Y.; Xie, L.G.; Hou, Y.T.; Hanif, D.S. On renewable sensor networks with wireless energy transfer. In Proceedings of the IEEE INFOCOM, Shanghai, China, 10–15 April 2011. [Google Scholar]
- Feng, Y.; Liu, N.B.; Wang, F.; Qian, Q.; Li, X.Q. Starvation avoidance mobile energy replenishment for wireless rechargeable sensor networks. In Proceedings of the IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016. [Google Scholar]
- Xie, L.G.; Shi, Y.; Hou, Y.T.; Hanif, D.S. Making sensor networks immortal: An energy-renewal approach with wireless power transfer. IEEE/ACM Trans. Netw. 2012, 6, 1748–1761. [Google Scholar] [CrossRef]
- Chen, T.Y.; Wei, H.W.; Cheng, Y.C.; Shi, W.K.; Chen, H.Y. An efficient routing algorithm to optimize the lifetime of sensor network using wireless charging vehicle. In Proceedings of the International Conference on Mobile Ad Hoc and Sensor Systems, Philadelphia, PA, USA, 28–30 October 2014. [Google Scholar]
- Xie, L.G.; Shi, Y.; Hou, Y.T.; Lou, W.J.; Sherali, H.D.; Midkiff, S.F. Multi-node wireless energy charging in sensor networks. IEEE/ACM Trans. Netw. 2015, 2, 437–450. [Google Scholar] [CrossRef]
- Pan, M.; Li, H.Y.; Pang, Y.W.; Yu, R.; Lu, Z.X.; Li, W. Optimal energy replenishment and data collection in wireless rechargeable sensor networks. In Proceedings of the IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014. [Google Scholar]
- Guo, S.T.; Wang, C.; Yang, Y.Y. Mobile data gathering with wireless energy replenishment in rechargeable sensor networks. In Proceedings of the IEEE INFOCOM, Turins, Italy, 14–19 April 2013. [Google Scholar]
- He, L.; Gu, Y.; Pan, J.P.; Zhu, T. On-demand charging in wireless sensor networks: Theories and applications. In Proceedings of the IEEE 10th International Conference on Mobile Ad-Hoc and Sensor Systems, Hangzhou, China, 14–16 October 2013. [Google Scholar]
- Zhu, J.Q.; Feng, Y.; Sun, H.Z.; Liu, M.; Zhang, Z.N. ESAOC: Energy starvation avoidance mobile charging for wireless rechargeable sensor networks. J. Softw. 2017. [Google Scholar] [CrossRef]
- Yusof, K.M.; Wood, J.; Fitz, S. Short-range and near ground propagation model for wireless sensor networks. In Proceedings of the IEEE Student Conference on Research and Development (SCOReD), Pulau Pinang, Malaysia, 5–6 December 2012. [Google Scholar]




















| Parameter | Symbol | Unit |
|---|---|---|
| Network size | M × L | m2 |
| Number of nodes | N | - |
| Sensing radius of node | Rs | m |
| Communication radius of node | Rt | m |
| Number of regions | k | - |
| Number of VTPs | m | - |
| Parameter | Symbol | Unit |
|---|---|---|
| Maximum time delay of packet uploading | Td | s |
| Speed of MDC | vMDC | m/s |
| The ith regular hexagons (i = 1, 2, …, m) | RHi | - |
| Number of nodes in RHi | Num (RHi) | - |
| Time for the MDC to stay at each VTP | ts | s |
| Sensing rate of node | g | bit/s |
| Data uploading rate of node | u | bit/s |
| A round of data gathering time of MDC | Tr | s |
| Buffer size of node | C | bit |
| Number of VTPs in the ith region (i = 1, 2, …, k) | - | |
| Path length of MDC in the ith region (i = 1, 2, …, k) | Di | m |
| Virtual traverse points | VTP | - |
| Base station | BS | - |
| Maximum time delay of packet transmission | s | |
| Maximum number of VTPs that MDC can traverse during Tr | m′ | - |
| Euclidean distance between BS and the first VTP | dBS to RHi | m |
| Minimum number of MDCs required in the network | k | - |
| Euclidean distance between two adjacent VTPs in the ith region (i = 1, 2, …, k) | D (j − 1, j) | m |
| Unit data collection period of MDC in the ith region (i = 1, 2, …, k) | T (j − 1, j) | s |
| Speed of MDC from VTPj−1 to VTPj after adjustment in the ith region (i = 1, 2, …, k) | vMDC (j − 1, j) | m/s |
| Symbol | Definition | Unit |
|---|---|---|
| Eelec | Energy consumption of the sending and receiving circuit | nJ/bit |
| εfs | Energy consumption of the amplifier in free-space model | pJ × (b/m2)−1 |
| Pi | Energy consumption rate of node i | J/s |
| dito VTP | Single-hop transmission distance of node i | m |
| es | Energy consumption rate of sensing | J/s |
| Nj | Number of nodes in the jth region | - |
| Cb | Battery capacity of sensor node | J |
| Ch | Battery Capacity of WCV | J |
| em | Energy consumption of WCV on travelling one meter | J/m |
| η | Wireless recharging rate | J/s |
| vWCV | Speed of WCV | m/s |
| γ | Residual energy threshold of WCV | J |
| Ф | Recharging request queue | - |
| Ψ | Queue of nodes waiting for recharging | - |
| Parameter | Symbol | Value |
|---|---|---|
| Network size | M × L | 300 m × 300 m–400 m × 400 m |
| Number of nodes | N | 923 |
| Length of the sensing radius | Rs | 10 m |
| Length of the communication radius | Rt | 10 m–30 m |
| Speed of MDC | vMDC | 5 m/s |
| Speed of WCV | vWCV | 5 m/s |
| Buffer size of one node | C | 12.7 KB |
| Data collection rate of one node | g | 130 bps |
| Data uploading rate of one node | u | 100 kbps |
| Maximum battery capacity of one node | Cb | 5 J |
| Maximum battery capacity of the WCV | Ch | 1 KJ |
| Energy consumption of the WCV on travelling one meter | em | 0.2 J |
| Wireless recharging rate | η | 0.1 J/s–0.5 J/s |
| Energy consumption of the sending and receiving circuit | Eelec | 50 nJ/bit |
| Energy consumption of the amplifier in free-space model | εfs | 10 pJ·(b/m2)−1 |
| Maximum delay for packet uploading | Td | 900 s–1700 s |
| Rt | 10 m | 20 m | 25 m | 30 m | ||
|---|---|---|---|---|---|---|
| Tr | ||||||
| Td | ||||||
| 900 s | 452 s | 455 s | 458 s | 460 s | ||
| 1000 s | 502 s | 506 s | 508 s | 511 s | ||
| 1200 s | 602 s | 606 s | 609 s | 612 s | ||
| 1400 s | 702 s | 707 s | 710 s | 713 s | ||
| 1500 s | 752 s | 757 s | 760 s | 764 s | ||
| 1600 s | 800 s | 800 s | 800 s | 800 s | ||
| 1700 s | 800 s | 800 s | 800 s | 800 s | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, C.; Wang, Q.-W.; Zhang, L.; Wang, R.-C. A High-Efficiency Data Collection Method Based on Maximum Recharging Benefit in Sensor Networks. Sensors 2018, 18, 2887. https://doi.org/10.3390/s18092887
Sha C, Wang Q-W, Zhang L, Wang R-C. A High-Efficiency Data Collection Method Based on Maximum Recharging Benefit in Sensor Networks. Sensors. 2018; 18(9):2887. https://doi.org/10.3390/s18092887
Chicago/Turabian StyleSha, Chao, Qi-Wei Wang, Lu Zhang, and Ru-Chuan Wang. 2018. "A High-Efficiency Data Collection Method Based on Maximum Recharging Benefit in Sensor Networks" Sensors 18, no. 9: 2887. https://doi.org/10.3390/s18092887
APA StyleSha, C., Wang, Q.-W., Zhang, L., & Wang, R.-C. (2018). A High-Efficiency Data Collection Method Based on Maximum Recharging Benefit in Sensor Networks. Sensors, 18(9), 2887. https://doi.org/10.3390/s18092887





