Next Article in Journal
High-Fidelity Inhomogeneous Ground Clutter Simulation of Airborne Phased Array PD Radar Aided by Digital Elevation Model and Digital Land Classification Data
Next Article in Special Issue
A Passive Tracking System Based on Geometric Constraints in Adaptive Wireless Sensor Networks
Previous Article in Journal
Backstepping Sliding Mode Control for Radar Seeker Servo System Considering Guidance and Control System
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sensors
Volume 18
Issue 9
10.3390/s18092926
sensors-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Evaluation of the Accuracy of Bathymetry on the Nearshore Coastlines of Western Korea from Satellite Altimetry, Multi-Beam, and Airborne Bathymetric LiDAR

by
Yeon Yeu
1,
Jurng-Jae Yee
2,
Hong Sik Yun
3 and
Kwang Bae Kim
3,*
1
National Research Center for Disaster-free and Safety Ocean City Construction, Dong-a University, Busan 49315, Korea
2
Department of Architectural Engineering, Dong-a University, Busan 49315, Korea
3
School of Civil, Architectural and Environmental System Engineering, Sungkyunkwan University, Suwon 16419, Korea
*
Author to whom correspondence should be addressed.
Sensors 2018, 18(9), 2926; https://doi.org/10.3390/s18092926
Submission received: 31 July 2018 / Revised: 30 August 2018 / Accepted: 30 August 2018 / Published: 3 September 2018
(This article belongs to the Special Issue Selected Papers from IEEE ICKII 2018)
Browse Figures
Versions Notes

Abstract

:
Bathymetric mapping is traditionally implemented using shipborne single-beam, multi-beam, and side-scan sonar sensors. Procuring bathymetric data near coastlines using shipborne sensors is difficult, however, this type of data is important for maritime safety, marine territory management, climate change monitoring, and disaster preparedness. In recent years, the bathymetric light detection and ranging (LiDAR) technique has been tried to get seamless geospatial data from land to submarine topography. This paper evaluated the accuracy of bathymetry generated near coastlines from satellite altimetry-derived gravity anomalies and multi-beam bathymetry using a tuning density contrast of 5000 kg/m3 determined by the gravity-geologic method. Comparing with the predicted bathymetry of using only multi-beam depth data, 78% root mean square error from both multi-beam and airborne bathymetric LiDAR was improved in shallow waters of nearshore coastlines of the western Korea. As a result, the satellite-derived bathymetry estimated from the multi-beam and the airborne bathymetric LiDAR was enhanced to the accuracy of about 0.2 m.

1. Introduction

Coastlines (or shorelines) have been investigated as one of the most important features on the Earth’s surface due to coastal erosion and flooding, adaptation to climate changes, coastal protection, environmental impact assessment, disaster management, and sustainable development. The information about coastlines and their changes is essential for coastal zone environmental management. In the past, coastlines were detected through ground surveying to generate coastline maps. As the technology has been developed, new methods were used to map coastlines. Aerial photographs were used for delineating and monitoring coastal erosion over a long coast in an efficient and economical way [1,2]. Global positioning system (GPS) is a useful technique for a spatial and temporal analysis. The beach face profile was observed by GPS and aerial photographs to examine shoreline mobility and sediment budget on a sandy coast over several years [3]. Coastline variations were determined by the real-time kinematic GPS technique as well as aerial photographs and historical cartography. The technique made it possible to identify shoreline changes and forecast of coastline evolution for more than 100 years [4]. Satellite remote sensing data, having various spectrum ranges, are examined to detect, extract, and monitor coastline changes [5]. Several shoreline mapping techniques on multi-temporal satellite data were compared [6]. Synthetic aperture radar (SAR), capable of all-weather imaging, can acquire images in cloudy and stormy weather as well as day-and-night conditions. The SAR imagery was investigated for mapping and monitoring sediment transport and for improving the quality of land/water body segmentation in order to derive the shorelines [7,8].
A light detection and ranging (LiDAR) system, a scanner system deflecting a laser beam and detecting its reflectance, was applied to detect the spatial patterns and volumetric amounts of coastline erosion along the beach face caused mainly by the tropical storms [9]. The combination of the airborne hyperspectral remote sensing and LiDAR provided a suitable data on the retrieval of the direction and amount of sediment transportation. This made it possible to analyze the dynamics of sandy shorelines and to monitor beach sediments for beach nourishments like the redistribution and the re-sorting of the fill in beach [10]. The unmanned aerial vehicle (UAV) system, a recent popular measuring platform, has increasingly been integrated into many applications. A UAV system was investigated to generate an accurate and valuable geo-information from high-resolution digital imagery at a low cost. The UAV system is an excellent tool for accurate surveys, especially for shallow inland lakes [11]. Accurate 3D representation generated by the UAV system was capable of detecting and visualizing coastal changes over time in order to manage a coastal zone environment [12]. Video cameras, that collect a sequence of images over one tidal cycle, were used to estimate the intertidal beach profile of the nearshore morphology [13]. The images of video cameras were explored to have a strong association with the presence of submerged sandbars through temporal analysis [14]. The video imagery could be utilized to optimize the sandbar estimation without regard to the hydrodynamic data.
Most methodologies focus on detecting and monitoring the coastline without considering the nearshore bathymetry data. The bathymetry data can produce a better understanding on the geomorphic evolution because of its capacity of including the coastlines as a part of its geomorphologic information. Furthermore, the bathymetric data are usually obtained by shipborne sonar sensors: single-beam, multi-beam, and sidescan sonar. A high resolution bathymetry was derived from multi-beam echo-sounders and bathymetric sidescan sonar systems. Due to the bathymetry, it was possible to determine bottom slope corrections and true angles of incidence as well as submarine topography [15]. Multi-beam sonar systems were applied to investigate the seafloor geomorphology from the continental shelf to the shallow-water (more than 10 m deep) coastal zone [16]. A high frequency multi-beam sonar applied to shallow seafloor acquired a bathymetric information that could produce an accurate height and seafloor surface orientation. This is good enough to detect a certain type of seafloor [17]. A sidescan sonar sensor was used to investigate tools for seabed sediments recognition based on accurate sediment data [18]. Thus far, bathymetric sonar is shown as an essential tool to generate seafloor geomorphology. It is impossible to acquire bathymetric data near coastlines with shipborne sonar equipment. This is, because of the depth of a nearshore zone is not deep enough to carry out any operation for a ship. Firstly introduced the gravity-geologic method (GGM) to derive the depth-to-basement of buried bedrock topography in geophysical mapping [19]. Later, satellite altimetry-derived gravity anomalies were adapted to predict bathymetry in the marine environment in several studies [20,21,22,23,24,25]. This is where the shipborne depth measurements are sparsely distributed and limited. A video-based technique has attempted to generate intertidal beach maps from low tide to high tide condition. This aimed to measure the location of the shoreline and monitor the foreshore changes [26]. The coastlines of intertidal beach were represented as horizontal planes as a function of the tidal elevation [27]. A model undertaking proper coastline management was proposed, and an automated procedure for intertidal beach bathymetry was presented using daily video images [28,29]. The limitation of the video-based technique is restricted to only the intertidal coastal areas.
There is a bathymetric data gap between the shallow seafloor obtained by the shipborne sonar and the intertidal coastal areas by video cameras. For this reason, a bathymetric LiDAR system was introduced. Due to viable laser returns retrieved from the seabed, a bathymetric LiDAR can detect up to sixty meters of depth in clear waters [30]. Furthermore, the LiDAR can provide highly resolved bathymetric data, especially in blue-green wavelength. This is a clear advantage of LiDAR systems in penetrating shallow clear water, generating almost seamless subaerial–submarine bathymetric map [31]. An airborne LiDAR system, developed by the US Army Corps of Engineers, enables monitoring the nearshore bathymetric environments with accurate, densely spaced bathymetric and topographic measurements [32]. A bathymetric LiDAR generates both topographic and bathymetric data to reveal erosional or depositional patterns and geomorphologic changes. This was used to investigate multi-year storm impacts using subaerial and subaqueous sediment volume changes [33].
Korea, located on a peninsula in north-eastern Asia, is comprised of western, southern, and eastern coastlines that have different characteristics in terms of their coastal environments. There are big tidal effects and the foreshore is widely distributed in the western coastal zones. Moreover, turbidity is high on western coastal zones due to unclear seawater and many floating materials. Southern coastlines are a typical ria coast and the shape of coastlines is very complicated with numerous islands and rocks.
This research aims to evaluate the accuracy of a satellite-derived bathymetry estimated by the GGM. This was generated by the combining sparse the Korea Hydrographic and Oceanographic Agency (KHOA) shipborne depth measurements obtained by the multi-beam instruments with a dense satellite altimetry-derived gravity anomalies in shallow waters near the shoreline. Satellite-derived bathymetry grid data were compared with the depth measurements on the KHOA ship tracks and airborne bathymetric LiDAR to assess its accuracy. Finally, this paper will present an improved satellite-derived bathymetry grid data in shallow waters and nearshore coastlines using all depth measurements. This includes the multi-beam and airborne bathymetric LiDAR, and satellite altimetry-derived gravity anomalies in this research.

2. Data sets and Methodology

2.1. Study Area

This study explores the bathymetry recovery using gravity effects extracted from the depth measurements, including multi-beam and bathymetric LiDAR, and satellite altimetry-derived gravity anomalies over shallow waters offshore Kaeyado Island, located on Ok-do myeon, Kunsan City on the West Sea of Korea. Figure 1 shows the selected study area (126.53°~126.55° E, 36.03°~36.05° N) that is in the shallow waters of the western part of Kaeyado. There are 2292 KHOA multi-beam shipborne locations. The 1528 KHOA multi-beam points are used for control points displayed as white triangles and 764 points are used for checkpoints as black circles. 1201 airborne bathymetric LiDAR points are displayed as red circles. The satellite altimetry-derived gravity anomalies by the Scripps Institution Oceanography [34,35] are displayed by colors.

2.2. Data Set

Both the land and the shallow seafloor were surveyed by bathymetric LiDAR and the seafloor measurements were completed by a multi-beam sonar in 2016. The multi-beam sensor is the Seabat 7125 hull mount sonar sensor manufactured by Reson (Slangerup, Denmark). The wavelength of the multi-beam is 400 kHz and the seafloor depth in the study area is less than 30 m. The bathymetric LiDAR sensor is a Coastal Zone Mapping Imaging LiDAR (CZMIL) manufactured by Optech (Vaughan, ON, Canada). The CMZIL uses two wavelengths of 1064 nm and 532 nm. The horizontal coordinates are UTM and its zone is 52. The vertical datum is not the mean sea level (MSL), but the approximate lowest low water (LLW). Table 1 represents the specifications of multi-beam, airborne bathymetric LiDAR, and satellite altimetry-derived gravity anomalies utilized in this study, as shown in Figure 1.
Multi-beam sonar systems are widely used for performing bathymetric surveying. The typical depth of the Seabat 7125 system is 0.5~150 m and the maximum depth is 17 m at 400 kHz. The depth resolution is 6 mm and, the maximum swath depth is 140° in equi-distance mode [35]. The minimum water depth for the sonar system is 1.5 m based on the draft of a ship’s hull and the typical depth of the system. The sonar system, however, typically requires more than 5 m of depth in water for safe operation. Airborne bathymetric LiDAR systems have the advantage of faster and cheaper surveying in shallow water and on coastlines due to a wide swath at aircraft speed. The horizontal and vertical accuracy of the CZMIL system is 3.5 + 0.05 × d meter and [0.32 + (0.013 × d)2]1/2 meter, respectively, where d is the water depth. The swath width the system is 70 percent of operating altitude. The major limitation of the LiDAR system is turbid and muddy water conditions. The maximum water depth of the LiDAR system depends on the diffuse attenuation coefficient (Kd). The maximum water depth of shallow and deep channel measurement is 2/Kd meter and 4.2/Kd meter, respectively [36]. Satellite altimetry-derived gravity anomalies generated by Envisat, CryoSat-2, and Jason-1 satellite altimeters are 1 mGal (=1 × 10−5 m/s2) accuracy for the global marine gravity field at a 1/2 wavelength spatial resolution of 7 km. The current accuracy of satellite altimetry-derived gravity anomalies is better than 1.7 mGal for latitudes less than 72° and lower accuracy (2~3 mGal) at higher latitudes depending on ice cover [37].

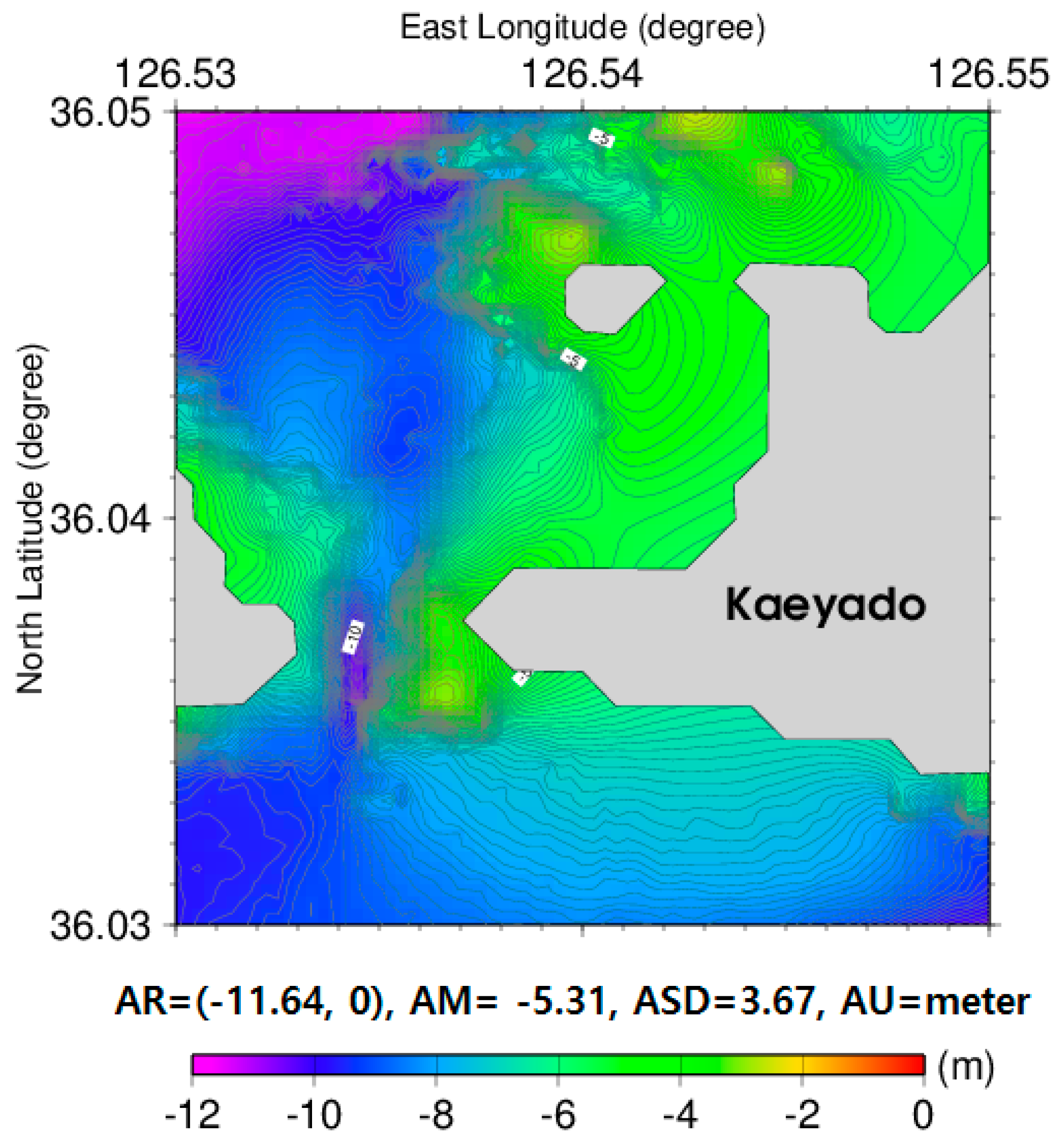
2.2.1. Multi-Beam

Before surveying, several calibrations are required. The first calibration is an offset calibration. There are several sensors like transducers, GPS, gyros as well as multi-beam in a hull mount sonar system, but because the sensors do not coincide with the ship’s center of gravity, accurate offsets between sensors and the center of gravity should be determined. The second one is a multi-beam bar-check. The multi-beam transmits a pan beam that drops a rectangular bar down the transmitter. The distance between the center of gravity and of this type of bar is verified similarly to the distance between the surface water and the bar. The third one is the calibration of the draft mark. This is the distance between the transducer and water surface. The draft mark is mainly dependent on the amount of fuel. The fourth one is the sonar speed calibration in seawater. The speed was approximately 1530 m/s. The last one is the orientation calibration after installing the hull mount multi-beam system. Even tough an error-free surveying system is installed in the wrong directions, the surveying results are incorrect. The orientation of the system is done by calibrating roll, heading, and pitch.
The Seabat hull mount sonar sensor radiates 240~516 beams in one ping as a pan beam. The surveyed data include the number of pings, data acquisition day/time, the location of data acquisition, vessel motion, gyro data, vessel speed, sonar speed in the sea, tidal data, draft mark and round trip times of the radiated multi-beam. Water depths are calculated by dividing a round trip time by the calibrated sonar speed with its consideration of the tidal effects. The bathymetric data are generated based on a World Geodetic System 1984 (WGS 84) ellipsoid and on a UTM 52 zone.

2.2.2. Bathymetric LiDAR

LiDAR measurements are made by the round-trip time between the emission of a laser pulse and the arrival of the return signal at the sensor’s receiver. A round-trip distance between the sensor and a target object is determined by multiplying the return signal’s elapsed time by the speed of light. A LiDAR system yields the 3D coordinates of a target object using the distance and the angle of a laser pulse. It is known as a topographic LiDAR. Unfortunately the topographic LiDAR is not suitable for the generation of the seafloor mapping. This is due to most of the laser pulses are returned from the water surface. For this reason, an Optech CZMIL bathymetric LiDAR uses two laser pulses: one is near-IR (1064 nm) laser pulse and the other is a green (532 nm) laser pulse. The former is reflected from the water surface and the latter is from the reflected seafloor topography. Infrared light can be used to detect the water surface location, because infrared light penetrates typical coastal waters very little. The green laser is partially reflected from the water surface and the sea bottom. Distances between the local sea surface and bottom could be calculated by the arrival time differences at the airborne receiver between water surface and sea bottom returns. The water depths at each location in a specific time can be determined by calculating distances between the sea surface and bottom, removing the effects of the wave height, correcting the speed of laser pulses in water, and converting tilted distance to vertical distance using the water nadir angle [38].
The LiDAR system consists of several pieces of equipment: laser, scanner, inertia measurement unit, and GPS. The offsets between a vehicle reference frame and each equipment are accurately calibrated. Scanner angle and boresight are an internal error caused by the movement or impact of the system and has its difficulty to be installed in the LiDAR system at the right directions. Therefore, scanner angle, boresight, roll, heading, and pitch are calibrated. The time interval of GPS is 1 Hz and the distance from the ground GPS reference stations are less than 30 km. The speed of an airplane is 40 knots and the scan angles are less than 20° in consideration of the data accuracy. The scanning pattern of CZMIL is in an elliptical shape. The ground spatial distance is nominally 2 m by 2 m using a deep channel measurement (10 kHz).
As mentioned in Section 2.2, the vertical datum of the multi-beam and LiDAR is different from the satellite altimetry-derived gravity anomalies. The depth from the approximate LLW should be transformed into the depth from the MSL for the next step. A tidebed model is set up from a six adjacent tide observations near the study location, and the calibration value of the depth between the LLW and MSL is decided approximately at 3.585 m. The depth from the MSL is calculated by adding 3.585 cm to the depth from the LiDAR system. The horizontal unit of satellite anomaly data is degree instead of the UTM coordinating system used in LiDAR and the multi-beam system. The Datum Level (DL) of the Kaeyado is 3.585 m below the local MSL provided from the multi-beam system. The multi-beam shipborne bathymetry based on the local MSL was calculated by subtracting 3.585 m from the multi-beam depth based on the DL.

2.2.3. Satellite Altimetry-Derived Gravity Anomaly

The satellite altimetry-derived gravity anomalies were obtained from Scripps Institution of Oceanography (SIO), University of California at San Diego. These were combined to determine a tuning density contrast for an accurate bathymetry prediction from the gravity effects in the off-tracks between ship tracks in shallow waters. The satellite altimetry-derived gravity anomaly data were re-gridded to 1 × 1 arc-seconds by using the “surface” routine, which is a continuous curvature splines, of Generic Mapping Tools (GMT) [39] from the 2 × 2 arc-minutes original data. The satellite altimetry-derived gravity anomalies in the study area showed a change between 16.3 and 18.6 mGal, as illustrated in the background in Figure 1.

2.3. Methodology

In this study, the GGM applied to several studies [20,21,22,23,24,25] to estimate the satellite derived bathymetry was implemented. Figure 2 shows the principles of bathymetry estimation by the GGM using the multi-beam depths of the known j-th control points.
The GGM applications to calculate the residual short wavelength gravity from a simple Bouguer term (=2πG(∆ρ)) with respect to the reference depth at known j-th control points are shown in Figure 2:
gshort(j) = 2πG(∆ρ)(d(j) − D),
where G is the gravitational constant, 6.672 × 10−11 m3 kg−1 s−2, ∆ρ is the density contrast (kg m−3), d(j) is the depth measurement at known j-th control points (m), and D is the deepest depth at a reference datum (m). The regional long wavelength gravity is generated by subtracting the residual gravity from observed gravity. This was calculated by interpolating the satellite altimetry-derived gravity anomalies at known j-th control points.
glong(j) = gobs(j) − gshort(j).
The regional long wavelength gravity at unknown i-th points were computed by gridding the regional gravity, glong(j), at known j-th control points. The residual short wavelength gravity at unknown i-th points are calculated from the difference between the observed gravity, gobs(i), and the regional gravity, glong(i):
gshort(i) = gobs(i) − glong(i),
where gobs(i) is the satellite altimetry-derived from the gravity anomalies.
Finally, the depth (d(i)) at unknown i-th points were calculated by summing the depth that was extracted by dividing the residual short wavelength gravity at unknown i-th points by a simple Bouguer term, and the deepest depth (D) as given in Equation (4):
d(i) = [gshort(i)/2πG(∆ρ)] + D.
In this study, a multi-beam shipborne bathymetry and satellite altimetry-derived gravity anomalies were used to predict the bathymetry in shallow waters around Kaeyado. The multi-beam shipborne bathymetry obtained from the KHOA pertains to the depth with respect to DL. This is the approximate LLW used in a reference surface on a nautical chart. The satellite altimetry-derived gravity anomalies are based on the sea surface, which is approximately the mean sea level. Consequently, the KHOA multi-beam depth measurements were converted to the depths based on the local mean sea level (LMSL) determined from the tidal observations of Kaeyado.
The tuning density contrast between the seawater and the seafloor topography is a very important factor as given in Equation (4) in order to effectively estimate the bathymetry from the short wavelength residual gravity. The estimation of bathymetry using the GGM is influenced by the distribution and number of the depths of known control points, the observed gravity, and the density contrast. The checkpoint method of the GGM was applied to determine a tuning density contrast for accurate bathymetry prediction, because the KHOA multi-beam depth data that have gaps between the shipborne tracks.
In this study, the 2292 KHOA multi-beam depth data were used for predicting the bathymetry by the checkpoints of the GGM. The KHOA multi-beam depth data in the study area were divided as 1528 control points (white triangles in Figure 1) and 764 check points (black circles in Figure 1), respectively, to calculate satellite-derived bathymetry estimation error by the GGM. The control points in the study area were analyzed for the stability of the GGM estimations over a range of density contrasts by the checkpoint method with GGM.

3. Results

Appropriate tuning density contrast was selected in a trade-off diagram that minimizes root mean square (RMS) errors of the GGM estimations. As shown in Figure 3, the tuning density contrast of about 5000 kg/m3 and greater was stabilized in the trade-off diagram, because the RMS errors level off as about 0.064 m along a circle of the blue curve. The tuning density contrast of 5000 kg/m3 in this study was chosen to predict satellite-derived bathymetry by the GGM, even though the theoretical density contrast between the seawater and the seafloor topography is 1670 kg/m3.
Figure 4a represents 1 arc-seconds gridded regional gravity anomalies computed from Equations (1) and (2). The residual gravity anomalies at unknown i-th points are estimated by subtracting the regional gravity anomalies (Figure 4a) from the satellite altimetry-derived gravity anomalies (background in Figure 1b), as illustrated in Figure 4b. These were utilized for the satellite derived bathymetry prediction that applies to the tuning density contrast of 5000 kg/m3 determined by the checkpoint method with the GGM in this study.
The 1 × 1 arc-seconds satellite-derived bathymetry grid data were estimated by the GGM using the tuning density contrast of 5000 kg/m3 as shown in Figure 5. Land parts of the islands that includes the Kaeyado in the 1 × 1 arc-seconds satellite derived bathymetry grid data were changed to zero values due to the depth being at a below zero value.
To evaluate the accuracy of the satellite-derived bathymetry grid data estimated by the GGM, the bathymetry grid was interpolated into the 2292 KHOA multi-beam shipborne locations. These are represented by the white triangles and the black circles in Figure 1. Figure 6a shows the absolute values of depth differences between the satellite-derived bathymetry and the KHOA multi-beam shipborne depths on the 2292 KHOA multi-beam shipborne tracks. As shown in Figure 6a, the statistics of the absolute values of the depth differences are summarized in Table 2.
In addition, the accuracy of satellite-derived bathymetry grid data estimated by the GGM was assessed by extrapolation on airborne bathymetric LiDAR locations that was not used for estimating bathymetry by the GGM. The absolute values of depth differences between satellite-derived bathymetry grid data estimated by the GGM and airborne bathymetric LiDAR were calculated to evaluate the accuracy of the 1201 airborne bathymetric LiDAR locations. These are represented by the red circles in Figure 1. According to the summarized statistics in Table 2, a satellite-derived bathymetry grid data estimated by the GGM in comparison with the airborne bathymetric LiDAR obtained in shallow waters near the shore of the northeastern areas of Kaeyado in Figure 6b shows a maximum difference of 5.49 m. The root mean square error (RMSE) of the absolute depth differences between GGM and KHOA in Table 2 is smaller than that of absolute depth differences between GGM and LiDAR.
The coefficient of determination (R2) was computed to validate the result of correlation between satellite-derived bathymetry by the GGM and KHOA multi-beam depth, and the GGM and airborne bathymetric LiDAR. As shown in Figure 7, GGM depth showed R2 of 0.986 with KHOA multi-beam depth; whereas, R2 between GGM depth and airborne bathymetric LiDAR was 0.739. M, L, and GGM in linear regression equation of Figure 7 denote multi-beam depth, airborne bathymetric LiDAR, and satellite-derived bathymetry by the GGM, respectively. These results may indicate that a satellite-derived bathymetry estimated by the GGM in shallow waters is more effective than nearshore.
An improved satellite-derived bathymetry estimated by the GGM (IGGM) using all depth measurements that includes a 2292 KHOA multi-beam and 1201 airborne bathymetric LiDAR with a density contrast of 5000 kg/m3 was illustrated in Figure 8 as its final result. Since density contrast determined by the GGM is approximately same in small areas, the IGGM was estimated with the assumption that there is no density contrast change. The IGGM of Figure 8 in comparison with the satellite-derived bathymetry estimated by the GGM of Figure 5 was enhanced in very shallow waters near the shore of the upper and left side of Kaeyado.
The IGGM was interpolated into KHOA multi-beam and airborne bathymetric LiDAR locations to compute the absolute differences of the depth for evaluating the accuracy of the improved satellite-derived bathymetry. As shown in Figure 9, the statistics of the absolute values of the depth differences are summarized in Table 3.
The improvement of the RMSE in terms of the absolute depth differences between IGGM and LiDAR in Table 3 is 78% [=(1.13 − 0.24)/1.13] in comparison with that of the absolute depth differences between GGM and LiDAR in Table 2. Whereas the RMSE of the absolute depth differences between IGGM and KHOA in Table 3 is enhanced with about 5% [=[0.19 − 0.18]/0.19], when comparing that of the absolute depth differences between GGM and KHOA in Table 2.
To compare correlation of between the IGGM and KHOA multi-beam depth, and between the IGGM and airborne bathymetric LiDAR, the coefficient of determination was calculated. The IGGM depth, as shown in Figure 10, showed R2 of 0.988 and 0.984 with KHOA multi-beam depth and airborne bathymetric LiDAR, respectively. M, L, and IGGM in linear regression equation of Figure 10 denote multi-beam depth, airborne bathymetric LiDAR, and improved satellite-derived bathymetry by the GGM, respectively. It is verified that the IGGM has strong correlation with KHOA multi-beam depth and airborne bathymetric LiDAR. The GGM can be effectively enhanced by combining multi-beam depth in shallow waters and airborne bathymetric LiDAR nearshore coastlines.
In addition, IGGM was interpolated into 3493 depth measurement locations. These are illustrated in Figure 1 to compute for the absolute differences of the depth for evaluating the accuracy of improved satellite-derived bathymetry. As shown in Figure 11, the minimum, maximum, mean, and standard deviation of the absolute depth differences are 0.00, 2.39, 0.10, and 0.18 m, respectively. The absolute depth differences below 0.20 m (the root mean square error (RMSE) in the statistics of Table 4) in Figure 11 were 86.7%. From small differences between IGGM and 3493 depth (multi-beam and airborne bathymetric LiDAR) data, we concluded that IGGM is enhanced by combining multi-beam depth and airborne bathymetric LiDAR in shallow waters near coastlines. IGGM depth was very highly correlated with 3493 depth (KHOA multi-beam and airborne bathymetric LiDAR) data with R2 of 0.992, as shown in Figure 12. ML and IGGM in linear regression equation of Figure 12 denote multi-beam depth and airborne bathymetric LiDAR, and improved satellite-derived bathymetry by the GGM, respectively.

4. Discussion

Since 2010, the gravity-geologic method in several studies [20,21,22,23,24] has been applied to predict accurate bathymetry in open sea with single tuning density contrast determined by satellite altimetry-derived gravity anomalies. In this study, multi-beam depth and airborne bathymetric LiDAR were used to enhance satellite-derived bathymetry in shallow waters near coastlines of the western Korea by the gravity-geologic method (GGM). In addition, dense satellite altimetry-derived gravity anomalies were utilized to determine a tuning density of 5000 kg/m3 in this study for generating accurate bathymetry by the GGM. According to the results of accuracy evaluation of bathymetry predicted by using only multi-beam depth, the satellite-derived bathymetry grid data had high coefficient of determination of 0.986 with multi-beam depth in shallow waters around Kaeyado Island; whereas, R2 was 0.739 with airborne bathymetric LiDAR in nearshore zones.
Both multi-beam depth and airborne bathymetric LiDAR were utilized to estimate an IGGM in nearshore zones of the upper and left side of Kaeyado. The IGGM was highly correlated with multi-beam depth and airborne bathymetric LiDAR as 0.988 and 0.984 in R2, respectively. In the accuracy evaluation of the IGGM, the improvement (78%) of the RMSE of the absolute depth differences between the IGGM and airborne bathymetric LiDAR is larger than that (5%) of the RMSE of the absolute depth differences between the IGGM and multi-beam depth.
By comparison with the accuracy of bathymetry predicted by only multi-beam depth data in shallow waters around Saemangeum Seawall of the West Sea of Korea in a recent study [25], the satellite-derived bathymetry estimated by combining multi-beam depth and airborne bathymetric LiDAR in this study was remarkably enhanced to the accuracy of 0.2 m in shallow waters near coastlines of the western Korea. Therefore, the gravity-geologic method has an advantage to improve bathymetry accuracy around nearshore by adding airborne bathymetry LiDAR that can observe depth values less than 5 m. This paper concludes that the satellite-derived bathymetry by the GGM can be effectively estimated with newly obtained multi-beam depth and airborne bathymetric LiDAR in shallow waters near coastlines in the future.

5. Conclusions

This study evaluated the accuracy of the two satellite-derived bathymetry (GGM and IGGM) estimated by the gravity-geologic method from satellite altimetry-derived gravity anomalies, KHOA multi-beam and airborne bathymetric LiDAR. The bathymetry predicted by the gravity-geologic method was improved by utilizing the topographic effects in the off-tracks computed from the satellite altimetry-derived gravity anomalies, and in the multi-beam and airborne bathymetric LiDAR for shallow waters near the shore of the western Korea. The RMSE of the IGGM was enhanced as accuracy of 0.2 m by using the multi-beam depth and airborne bathymetric LiDAR. This could lead to statistically showing the significant improvement of the shallow waters near coastlines in comparison with that of the GGM. In future studies, the depth data obtained from the airborne bathymetric LiDAR will be applied to enhance the accuracy of bathymetry in shallow waters near the coastlines.

Author Contributions

Y.Y. conceptualized this research, conducted the data processing, wrote methodology, and revised the manuscript. J.-J.Y. supported a funding and administrated the research. H.S.Y. gave comments and suggestions to improve this manuscript. K.B.K. was responsible for the original idea and research design. He also performed experiments regarding data analysis.

Funding

This research was funded by Basic Science Research Program through the National Research Foundation of Korea (NRF) grant funded by the Ministry of Education, grant number 2016R1A6A1A03012812.

Acknowledgments

The authors wish to thank the Korea Hydrographic and Oceanographic Agency (KHOA), which provided authorization to access geo-spatial data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Stafford, D.B.; Langfelder, J. Air photo survey of coastal erosion. Photogramm. Eng. 1971, 37, 565–575. [Google Scholar]
  2. Moore, L.J.; Benumof, B.T.; Griggs, G.B. Coastal erosion hazards in Santa Cruz and San Diego Counties, California. J. Coastal Res. 1999, SI28, 121–139. [Google Scholar]
  3. Battiau-Queney, Y.; Billet, J.F.; Chaverot, S.; Lanoy-Ratel, P. Recent shoreline mobility and geomorphologic evolution of macrotidal sandy beaches in the north of France. Mar. Geol. 2003, 194, 31–45. [Google Scholar] [CrossRef]
  4. Aiello, A.; Canora, F.; Pasquariello, G.; Spilotro, G. Shoreline variations and coastal dynamics: A space–time data analysis of the Jonian littoral, Italy. Estuar. Coast. Shelf Sci. 2013, 129, 124–135. [Google Scholar] [CrossRef]
  5. Alesheikh, A.A.; Ghorbanali, A.; Nouri, N. Coastline change detection using remote sensing. Int. J. Environ. Sci. Technol. 2007, 4, 61–66. [Google Scholar] [CrossRef] [Green Version]
  6. Sunder, S.; Ramsankaran, R.A.A.J.; Ramakrishnan, B. Inter-comparison of remote sensing sensing-based shoreline mapping techniques at different coastal stretches of India. Environ. Monit. Assess. 2017, 189, 290. [Google Scholar] [CrossRef] [PubMed]
  7. Niedermeier, A.; Romaneessen, E.; Lehner, S. Detection of coastlines in SAR images using wavelet methods. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2270–2281. [Google Scholar] [CrossRef]
  8. Demir, N.; Oy, S.; Erdem, F.; Seker, D.Z.; Bayram, B. Integrated shoreline extraction approach with use of Rasat MS and SENTINEL-1A SAR Images. ISPRS Annals of Photogramm. Remote Sens. Spa. Inf. Sci. 2017, 445–449. [Google Scholar] [CrossRef]
  9. White, S.A.; Wang, Y. Utilizing DEMs derived from LIDAR data to analyze morphologic change in the North Carolina coastline. Remote Sens. Environ. 2003, 85, 39–47. [Google Scholar] [CrossRef]
  10. Deronde, B.; Houthuys, R.; Henriet, J.P.; Lancker, V.V. Monitoring of the sediment dynamics along a sandy shoreline by means of airborne hyperspectral remote sensing and LIDAR: A case study in Belgium. Earth Surf. Proc. Land. 2008, 33, 280–294. [Google Scholar] [CrossRef]
  11. Templin, T.; Popielarczyk, D.; Kosecki, R. Application of low-cost fixed-wing UAV for inland lakes shoreline investigation. Pure Appl. Geophys. 2017, 1–21. [Google Scholar] [CrossRef]
  12. Topouzelis, K.; Papakonstantinou, A.; Doukari, M. Coastline change detection using Unmanned Aerial Vehicles and image processing technique. Fresen. Environ. Bull. 2017, 26, 5564–5571. [Google Scholar]
  13. Plant, N.G.; Holman, R.A. Intertidal beach profile estimation using video images. Mar. Geol. 1997, 140, 1–24. [Google Scholar] [CrossRef]
  14. Guedes, R.M.; Calliari, L.J.; Holland, K.T.; Plant, N.G.; Pereira, P.S.; Alves, F.N. Short-term sandbar variability based on video imagery: comparison between time–average and time–variance techniques. Mar. Geol. 2011, 289, 122–134. [Google Scholar] [CrossRef]
  15. De Moustier, C.; Matsumoto, H. Seafloor acoustic remote sensing with multibeam echo-sounders and bathymetric sidescan sonar systems. Mar. Geophys. Res. 1993, 15, 27–42. [Google Scholar] [CrossRef] [Green Version]
  16. Hughes Clarke, J.E.; Mayer, L.A.; Wells, D.E. Shallow-water imaging multibeam sonars: A new tool for investigating seafloor processes in the coastal zone and on the continental shelf. Mar. Geophys. Res. 1996, 18, 607–629. [Google Scholar] [CrossRef]
  17. Canepa, G.; Pace, N.G. Seafloor segmentation from multibeam bathymetric sonar. In Proceedings of the Fifth European Conference on Underwater Acoustics, Lyon, France, 10–13 July 2000; pp. 361–366. [Google Scholar]
  18. Atallah, L.; Smith, P.J.P.; Bates, C.R. Wavelet analysis of bathymetric sidescan sonar data for the classification of seafloor sediments in Hopvågen Bay-Norway. Mar. Geophys. Res. 2002, 23, 431–442. [Google Scholar] [CrossRef]
  19. Ibrahim, A.; Hinze, W.J. Mapping Buried Bedrock Topography with Gravity. Ground Water. 1972, 10, 18–23. [Google Scholar] [CrossRef]
  20. Kim, K.B.; Hsiao, Y.-S.; Kim, J.W.; Lee, B.Y.; Kwon, Y.K.; Kim, C.H. Bathymetry enhancement by altimetry-derived gravity anomalies in the East Sea (Sea of Japan). Mar. Geophys. Res. 2010, 31, 285–298. [Google Scholar] [CrossRef]
  21. Hsiao, Y.-S.; Kim, J.W.; Kim, K.B.; Lee, B.Y.; Hwang, C. Bathymetry estimation by gravity-geologic method: Investigation of density contrast predicted by downward continuation. Terr. Atmos. Ocean. Sci. 2011, 22, 347–358. [Google Scholar] [CrossRef]
  22. Kim, J.W.; von Frese, R.R.B.; Lee, B.Y.; Roman, D.R.; Doh, S.J. Altimetry-derived gravity predictions of bathymetry by gravity-geologic method. Pure Appl. Geophys. 2011, 168, 815–826. [Google Scholar] [CrossRef]
  23. Kim, K.B.; Lee, C.K. Bathymetry change investigation of the 2011 Tohoku earthquake. J. Kor. Soc. Surv. Geodesy Photogramm. Cartogr. 2015, 33, 181–192. [Google Scholar] [CrossRef]
  24. Hsiao, Y.-S.; Hwang, C.; Cheng, Y.-S.; Chen, L.-C.; Hsu, H.-J.; Tsai, J.-H.; Liu, C.-L.; Wang, C.-C.; Liu, Y.-C.; Kao, Y.-C. High-resolution depth and coastline over major atolls of South China Sea from satellite altimetry and imagery. Remote Sens. Environ. 2016, 176, 69–83. [Google Scholar] [CrossRef]
  25. Kim, K.B.; Yun, H.S. Satellite-derived Bathymetry Prediction in Shallow Waters Using the Gravity-Geologic Method: A Case Study in the West Sea of Korea. KSCE J. Civ. Eng. 2018, 22, 2560–2568. [Google Scholar] [CrossRef]
  26. Aarninkhof, S.G.J.; Turner, I.L.; Dronkers, T.D.T.; Caljouw, M.; Nipius, L. A video-based technique for mapping intertidal beach bathymetry. Coast. Eng. 2003, 49, 275–289. [Google Scholar] [CrossRef]
  27. Bergsma, E.W.J.; Conley, D.C.; Davidson, M.A.; O’Hare, T.J. Video-based nearshore bathymetry estimation in macro-tidal environments. Mar. Geol. 2016, 374, 31–41. [Google Scholar] [CrossRef]
  28. Osorio, A.F.; Medina, R.; Gonzalez, M. An algorithm for the measurement of shoreline and intertidal beach profiles using video imagery: PSDM. Comput. Geosci. 2012, 46, 196–207. [Google Scholar] [CrossRef]
  29. Uunk, L.; Wijnberg, K.M.; Morelissen, R. Automated mapping of the intertidal beach bathymetry from video images. Coast. Eng. 2010, 57, 461–469. [Google Scholar] [CrossRef]
  30. Wang, C.K.; Philpot, W.D. Using airborne bathymetric lidar to detect bottom type variation in shallow waters. Remote Sens. Environ. 2007, 106, 123–135. [Google Scholar] [CrossRef]
  31. Brock, J.C.; Purkis, S.J. The emerging role of lidar remote sensing in coastal research and resource management. J. Coastal Res. 2009, SI53, 1–5. [Google Scholar] [CrossRef]
  32. Irish, J.L.; McClung, J.K.; Lillycrop, W.J. Airborne Lidar Bathymetry: The SHOALS System; U.S. Army Corps of Engineer, Mobile District: Mobile, AL, USA, 2016. [Google Scholar]
  33. Eisemann, E.R.; Wallace, D.J.; Buijsman, M.C.; Pierce, T. Response of a vulnerable barrier island to multi-year storm impacts: LiDAR-data-inferred morphodynamic changes on Ship Island, Mississippi, USA. Geomorphology 2018, 313, 58–71. [Google Scholar] [CrossRef]
  34. Sandwell, D.T.; Smith, W.H.F. Global marine gravity from retracked Geosat and ERS-1 altimetry: Ridge segmentation versus spreading rate. J. Geophys. Res. 2009, 114, B01411. [Google Scholar] [CrossRef]
  35. Teledyne Marine. Available online: http://www.teledynemarine.com/ (accessed on 24 July 2018).
  36. Teledyne Optech. Available online: http://www.teledyneoptech.com/ (accessed on 24 July 2018).
  37. Sandwell, D.T.; Garcia, E.; Soofi, K.; Wessel, P.; Chandler, M.; Smith, W.H.F. Toward 1-mGal accuracy in global marine gravity from CryoSat-2, Envisat, and Jason-1. Lead. Edge 2013, 32, 892–899. [Google Scholar] [CrossRef]
  38. Guenther, G.C. Airborne lidar bathymetry. In Digital Elevation Model Technologies and Applications: The DEM Users Manual, 2nd ed.; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2007; pp. 253–320. [Google Scholar]
  39. Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic Mapping Tools: Improved version released. EOS Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef]
Sensors 18 02926 g001 550
Figure 1. (a) Location map of the study area. (b) 2292 KHOA multi-beam shipborne locations (white triangles and black circles) and 1201 airborne bathymetric LiDAR locations (red circles); and satellite altimetry-derived gravity anomalies (as a background). AR: amplitude range (=minimum and maximum values); AM: amplitude mean; ASD: amplitude standard deviation; AU: amplitude unit.
Figure 1. (a) Location map of the study area. (b) 2292 KHOA multi-beam shipborne locations (white triangles and black circles) and 1201 airborne bathymetric LiDAR locations (red circles); and satellite altimetry-derived gravity anomalies (as a background). AR: amplitude range (=minimum and maximum values); AM: amplitude mean; ASD: amplitude standard deviation; AU: amplitude unit.
Sensors 18 02926 g001
Sensors 18 02926 g002 550
Figure 2. The principle of the gravity geologic method (GGM) to estimate bathymetry (modified from [23]).
Figure 2. The principle of the gravity geologic method (GGM) to estimate bathymetry (modified from [23]).
Sensors 18 02926 g002
Sensors 18 02926 g003 550
Figure 3. Trade-off diagram for selecting a tuning density contrast of 5000 kg/m3 in the study area. RMS: root mean square.
Figure 3. Trade-off diagram for selecting a tuning density contrast of 5000 kg/m3 in the study area. RMS: root mean square.
Sensors 18 02926 g003
Sensors 18 02926 g004 550
Figure 4. (a) 1 arc-seconds regional long wavelength gravity anomalies and (b) 1 arc-seconds residual short wavelength gravity anomalies in the study area.
Figure 4. (a) 1 arc-seconds regional long wavelength gravity anomalies and (b) 1 arc-seconds residual short wavelength gravity anomalies in the study area.
Sensors 18 02926 g004
Sensors 18 02926 g005 550
Figure 5. 1 arc-seconds satellite-derived bathymetry grid data estimated by the GGM using a tuning density contrast of 5000 kg/m3.
Figure 5. 1 arc-seconds satellite-derived bathymetry grid data estimated by the GGM using a tuning density contrast of 5000 kg/m3.
Sensors 18 02926 g005
Sensors 18 02926 g006 550
Figure 6. (a) Absolute differences of depth between the GGM and KHOA on the 2292 KHOA multi-beam shipborne tracks. (b) Absolute differences of depth between the GGM and airborne bathymetric LiDAR on the 1201 airborne bathymetric LiDAR locations.
Figure 6. (a) Absolute differences of depth between the GGM and KHOA on the 2292 KHOA multi-beam shipborne tracks. (b) Absolute differences of depth between the GGM and airborne bathymetric LiDAR on the 1201 airborne bathymetric LiDAR locations.
Sensors 18 02926 g006
Sensors 18 02926 g007 550
Figure 7. (a) The coefficient of determination (R2) between GGM depth and multi-beam depth and (b) the coefficient of determination between GGM depth and airborne bathymetric LiDAR by linear regression.
Figure 7. (a) The coefficient of determination (R2) between GGM depth and multi-beam depth and (b) the coefficient of determination between GGM depth and airborne bathymetric LiDAR by linear regression.
Sensors 18 02926 g007
Sensors 18 02926 g008 550
Figure 8. Improved satellite-derived bathymetry estimated by the GGM.
Figure 8. Improved satellite-derived bathymetry estimated by the GGM.
Sensors 18 02926 g008
Sensors 18 02926 g009 550
Figure 9. (a) Absolute differences of depth between IGGM and KHOA on the 2292 KHOA multi-beam shipborne tracks. (b) Absolute differences of depth between IGGM and airborne bathymetric LiDAR on the 1201 airborne bathymetric LiDAR locations.
Figure 9. (a) Absolute differences of depth between IGGM and KHOA on the 2292 KHOA multi-beam shipborne tracks. (b) Absolute differences of depth between IGGM and airborne bathymetric LiDAR on the 1201 airborne bathymetric LiDAR locations.
Sensors 18 02926 g009
Sensors 18 02926 g010 550
Figure 10. (a) The coefficient of determination between IGGM depth and multi-beam depth and (b) the coefficient of determination between IGGM depth and airborne bathymetric LiDAR by linear regression.
Figure 10. (a) The coefficient of determination between IGGM depth and multi-beam depth and (b) the coefficient of determination between IGGM depth and airborne bathymetric LiDAR by linear regression.
Sensors 18 02926 g010
Sensors 18 02926 g011 550
Figure 11. Absolute differences of depth between IGGM and 3493 depth (multi-beam and airborne bathymetric LiDAR) data.
Figure 11. Absolute differences of depth between IGGM and 3493 depth (multi-beam and airborne bathymetric LiDAR) data.
Sensors 18 02926 g011
Sensors 18 02926 g012 550
Figure 12. The coefficient of determination between IGGM depth and 3493 depth (multi-beam and airborne bathymetric LiDAR) data by linear regression.
Figure 12. The coefficient of determination between IGGM depth and 3493 depth (multi-beam and airborne bathymetric LiDAR) data by linear regression.
Sensors 18 02926 g012
Table
Table 1. The specification of multi-beam, airborne bathymetric light detection and ranging (LiDAR), and satellite altimetry-derived gravity anomalies. CZMIL: Coastal Zone Mapping Imaging LiDAR; WGS: World Geodetic System.
Table 1. The specification of multi-beam, airborne bathymetric light detection and ranging (LiDAR), and satellite altimetry-derived gravity anomalies. CZMIL: Coastal Zone Mapping Imaging LiDAR; WGS: World Geodetic System.
TypeMulti-Beam BathymetryAirborne Bathymetric LiDARSatellite Altimetry-Derived Gravity Anomalies
SensorSeabat 7125CZMILAltimeter
Platformshipborneairbornespaceborne
EllipsoidWGS-84WGS-84WGS-84
UnitmetermetermGal
Reference surfaceDatum LevelDatum LevelMean Sea Level
Table
Table 2. Statistics of absolute values of depth differences between GGM and Korea Hydrographic and Oceanographic Agency (KHOA) multi-beam and between GGM and bathymetric LiDAR (Unit: meter).
Table 2. Statistics of absolute values of depth differences between GGM and Korea Hydrographic and Oceanographic Agency (KHOA) multi-beam and between GGM and bathymetric LiDAR (Unit: meter).
Min.Max.MeanStd. Dev.RMSE
GGM–KHOA0.002.440.080.180.19
GGM–LiDAR0.005.490.650.931.13
Table
Table 3. Statistics of absolute values of depth differences between the improved GGM (IGGM) and KHOA multi-beam and between the IGGM and bathymetric LiDAR (Unit: meter).
Table 3. Statistics of absolute values of depth differences between the improved GGM (IGGM) and KHOA multi-beam and between the IGGM and bathymetric LiDAR (Unit: meter).
Min.Max.MeanStd. Dev.RMSE
IGGM–KHOA0.002.390.080.160.18
IGGM–LiDAR0.001.800.140.190.24
Table
Table 4. Statistics of absolute values of depth differences between IGGM and 3493 (KHOA multi-beam and airborne bathymetric LiDAR) depth locations (Unit: meter).
Table 4. Statistics of absolute values of depth differences between IGGM and 3493 (KHOA multi-beam and airborne bathymetric LiDAR) depth locations (Unit: meter).
Min.Max.MeanStd. Dev.RMSE
IGGM − (KHOA + LiDAR)0.002.390.100.180.20

Share and Cite

MDPI and ACS Style

Yeu, Y.; Yee, J.-J.; Yun, H.S.; Kim, K.B. Evaluation of the Accuracy of Bathymetry on the Nearshore Coastlines of Western Korea from Satellite Altimetry, Multi-Beam, and Airborne Bathymetric LiDAR. Sensors 2018, 18, 2926. https://doi.org/10.3390/s18092926

AMA Style

Yeu Y, Yee J-J, Yun HS, Kim KB. Evaluation of the Accuracy of Bathymetry on the Nearshore Coastlines of Western Korea from Satellite Altimetry, Multi-Beam, and Airborne Bathymetric LiDAR. Sensors. 2018; 18(9):2926. https://doi.org/10.3390/s18092926

Chicago/Turabian Style

Yeu, Yeon, Jurng-Jae Yee, Hong Sik Yun, and Kwang Bae Kim. 2018. "Evaluation of the Accuracy of Bathymetry on the Nearshore Coastlines of Western Korea from Satellite Altimetry, Multi-Beam, and Airborne Bathymetric LiDAR" Sensors 18, no. 9: 2926. https://doi.org/10.3390/s18092926

APA Style

Yeu, Y., Yee, J. -J., Yun, H. S., & Kim, K. B. (2018). Evaluation of the Accuracy of Bathymetry on the Nearshore Coastlines of Western Korea from Satellite Altimetry, Multi-Beam, and Airborne Bathymetric LiDAR. Sensors, 18(9), 2926. https://doi.org/10.3390/s18092926

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop