Measurement Structures of Image Compressive Sensing for Green Internet of Things (IoT)
Abstract
:1. Introduction
1.1. Motivation and Objective
1.2. Related Work
1.3. Main Contribution
2. Traditional Structures
2.1. Whole Structure
2.2. Block Structure
3. Three Potential Structures
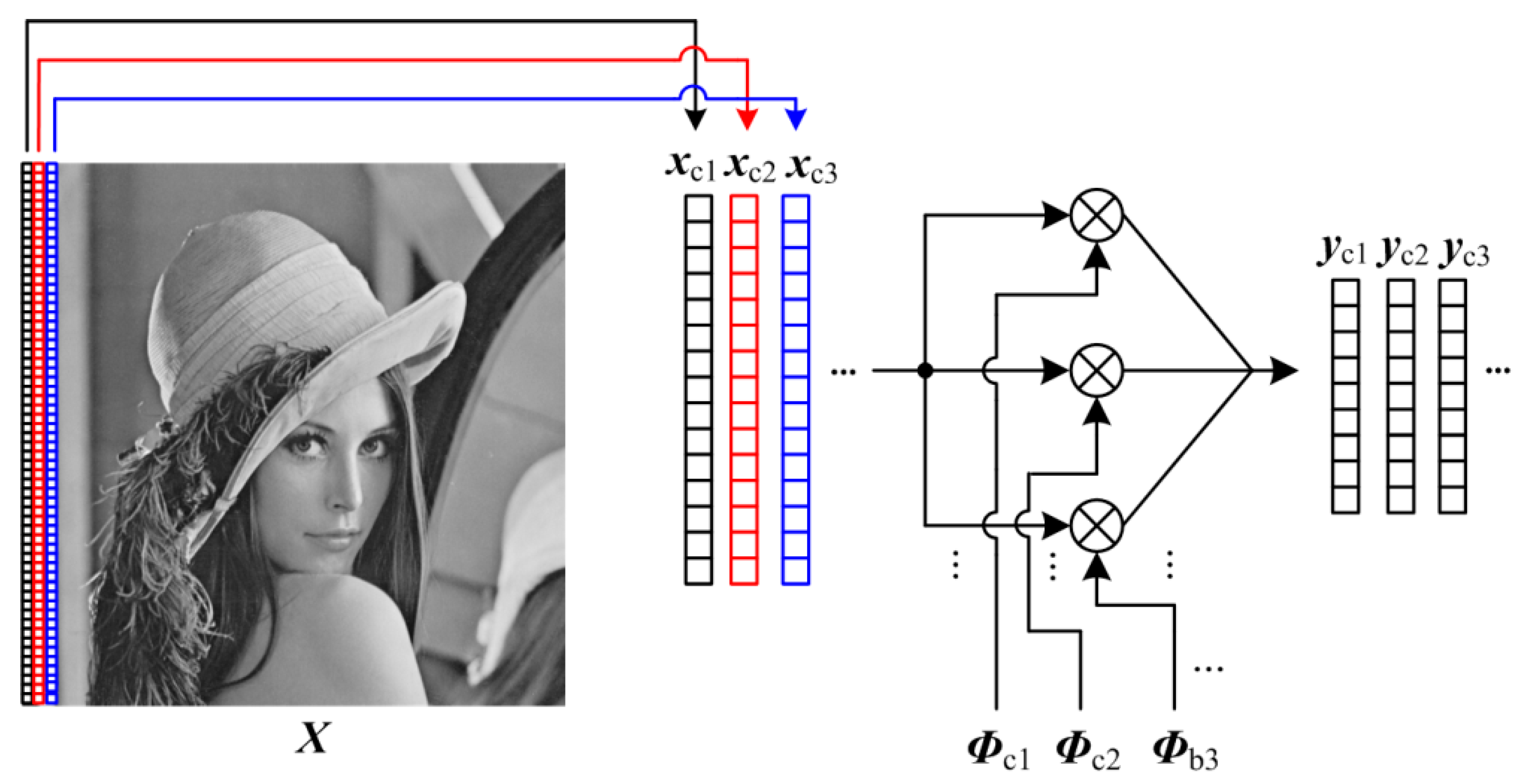
3.1. Raster Structure
3.2. Patch Structure
3.3. Layered Structure
4. Experimental Results
4.1. Subjective Evaluation
4.2. Objective Evaluation
4.3. Effects of Measurement Matrices
4.4. Effects of Recovery Algorithms
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Baraniuk, R.G.; Goldstein, T.; Sankaranarayanan, A.C.; Studer, C.; Veeraraghavan, A.; Wakin, M.B. Compressive video sensing: Algorithms, architectures, and applications. IEEE Signal Process. Mag. 2017, 34, 52–66. [Google Scholar] [CrossRef]
- Candè, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Mun, S.; Fowler, J.E. Motion-compensated compressed-sensing reconstruction for dynamic MRI. In Proceedings of the 2013 IEEE International Conference on Image Processing, Melbourne, Australia, 15–18 September 2013; pp. 1006–1010. [Google Scholar]
- Li, C.; Sun, T.; Kelly, K.F.; Zhang, Y. A compressive sensing and unmixing scheme for hyperspectral data processing. IEEE Trans. Image Process. 2012, 21, 1200–1210. [Google Scholar] [PubMed]
- Wu, J.; Liu, F.; Jiao, L.C.; Wang, X. Compressive sensing SAR image reconstruction based on Bayesian framework and evolutionary computation. IEEE Trans. Image Process. 2011, 20, 1904–1911. [Google Scholar] [CrossRef] [PubMed]
- Bevacqua, M.T.; Crocco, L.; Donato, L.D.; Isernia, T. Non-linear inverse scattering via sparsity regularized contrast source inversion. IEEE Trans. Comput. Imaging 2017, 3, 296–304. [Google Scholar] [CrossRef]
- Bevacqua, M.T.; Isernia, T. Boundary indicator for aspect limited sensing of hidden dielectric objects. IEEE Geosci. Remote Sens. Lett. 2018, 15, 838–842. [Google Scholar] [CrossRef]
- Morabito, A.F. Synthesis of maximum-efficiency beam arrays via convex programming and compressive sensing. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2404–2407. [Google Scholar] [CrossRef]
- Morabito, A.F.; Rocca, P. Reducing the number of elements in phase-only reconfigurable arrays generating sum and difference patterns. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1338–1341. [Google Scholar] [CrossRef]
- Arshad, R.; Zahoor, S.; Shah, M.A.; Wahid, A.; Yu, H. Green IoT: An investigation on energy saving practices for 2020 and beyond. IEEE Access 2017, 5, 15667–15681. [Google Scholar] [CrossRef]
- Hu, J.; Luo, J.; Zheng, Y.; Li, K. Graphene-grid deployment in energy harvesting cooperative wireless sensor networks for Green IoT. IEEE Trans. Ind. Inform. 2018. [Google Scholar] [CrossRef]
- Colonnese, S.; Biagi, M.; Cattai, T.; Cusani, R.; De Vico Fallani, F.; Scarano, G. Green compressive sampling reconstruction in IoT networks. Sensors 2018, 18, 2735. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Ahammad, P.; Boyer, C.; Huang, S.I.; Lin, L.; Lobaton, E.; Meingast, M.; Oh, S.; Wang, S.; Yan, P.; et al. CITRIC: A low-bandwidth wireless camera network platform. In Proceedings of the ACM/IEEE International Conference on Distributed Smart Cameras, Stanford, CA, USA, 7–11 September 2008; pp. 1–10. [Google Scholar]
- Asif, M.S.; Fernandes, F.; Romberg, J. Low-complexity video compression and compressive sensing. In Proceedings of the 2013 Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 2013; pp. 579–583. [Google Scholar]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A.T. A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef]
- Becker, S.; Bobin, J.; Candès, E.J. NESTA: A fast and accurate first-order method for sparse recovery. SIAM J. Imaging Sci. 2011, 4, 1–39. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Do, T.T.; Gan, L.; Nguyen, N.H.; Tran, T.D. Fast and efficient compressive sensing using structurally random matrices. IEEE Trans. Signal Process. 2012, 60, 139–154. [Google Scholar] [CrossRef]
- Zhang, P.; Gan, L.; Sun, S.; Ling, C. Modulated unit-norm tight frames for compressed sensing. IEEE Trans. Signal Process. 2015, 63, 3974–3985. [Google Scholar] [CrossRef]
- Hsieh, S.H.; Lu, C.S.; Pei, S.C. Compressive sensing matrix design for fast encoding and decoding via sparse FFT. IEEE Signal Process. Lett. 2018, 25, 591–595. [Google Scholar] [CrossRef]
- Gan, L. Block compressed sensing of natural images. In Proceedings of the 2007 15th International Conference on Digital Signal Processing, Cardiff, UK, 1–4 July 2007; pp. 403–406. [Google Scholar]
- Mun, S.; Fowler, J.E. Block compressed sensing of images using directional transforms. In Proceedings of the 2009 16th IEEE International Conference on Image Processing, Cairo, Egypt, 7–10 November 2009; pp. 3021–3024. [Google Scholar]
- Yu, Y.; Wang, B.; Zhang, L. Saliency-based compressive sampling for image signals. IEEE Signal Process. Lett. 2010, 17, 973–976. [Google Scholar]
- Zhang, J.; Xiang, Q.; Yin, Y.; Chen, C.; Luo, X. Adaptive compressed sensing for wireless image sensor networks. Multimedia Tools and Applications. Multimed. Tools Appl. 2017, 76, 4227–4242. [Google Scholar] [CrossRef]
- Mun, S.; Fowler, J.E. DPCM for quantized block-based compressed sensing of images. In Proceedings of the 2012 Proceedings of the 20th European Signal Processing Conference, Bucharest, Romania, 27–31 August 2012; pp. 1424–1428. [Google Scholar]
- Wang, L.; Wu, X.; Shi, G. Binned progressive quantization for compressive sensing. IEEE Trans. Image Process. 2012, 21, 2980–2990. [Google Scholar] [CrossRef] [PubMed]
- Dinh, K.Q.; Shim, H.J.; Jeon, B. Measurement coding for compressive imaging using a structural measuremnet matrix. In Proceedings of the 2013 IEEE International Conference on Image Processing, Melbourne, Australia, 15–18 September 2013; pp. 10–13. [Google Scholar]
- Gao, X.; Zhang, J.; Che, W.; Fan, X.; Zhao, D. Block-based compressive sensing coding of natural images by local structural measurement matrix. In Proceedings of the 2015 Data Compression Conference, Snowbird, UT, USA, 7–9 April 2015; pp. 133–142. [Google Scholar]
- Duarte, M.; Wakin, M.; Baraniuk, R. Fast reconstruction of piecewise smooth signals from incoherent projections. Presented at the Workshop on Signal Processing with Adaptive Sparse Structured Representations, Rennes, France, 16–18 November 2005; pp. 1–4. [Google Scholar]
- Baraniuk, R.; Davenport, M.; DeVore, R. A simple proof of the restricted isometry property for random matrices. Constr. Approx. 2008, 28, 253–263. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]










| CS | Compressive Sensing |
| Green IoT | Green Internet of Things |
| WH | Whole Structure |
| BL | Block Structure |
| RA | Raster Structure |
| PA | Patch Structure |
| LA | Layered Structure |
| SQ | Scalar Quantization |
| DPCM | Differential Pulse Code Modulation |
| SRM | Structurally Random Matrix |
| DCT | Discrete Cosine Transform |
| FFT | Fast Fourier Transform |
| GPSR | Gradient Projection for Sparse Reconstruction |
| PSNR | Peak Signal-to-Noise Ratio |
| Subrate | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | Average |
|---|---|---|---|---|---|---|
| WH | 30.68 | 31.17 | 31.57 | 31.97 | 33.28 | 31.74 |
| BL | 16.09 | 16.63 | 17.46 | 18.57 | 19.52 | 17.65 |
| RA | 6.82 | 8.57 | 10.69 | 12.91 | 15.31 | 10.86 |
| PA | 33.01 | 35.72 | 36.06 | 37.36 | 38.12 | 36.05 |
| LA | 16.66 | 17.37 | 18.46 | 19.31 | 20.41 | 18.44 |
| Subrate | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | Average |
|---|---|---|---|---|---|---|
| WH | 1.22 × 105 | 1.00 × 105 | 0.65 × 105 | 0.52 × 105 | 0.31 × 105 | 0.74 × 105 |
| BL | 10.12 | 10.21 | 10.16 | 10.14 | 10.33 | 10.19 |
| RA | 5.67 | 7.92 | 8.66 | 10.05 | 12.88 | 9.04 |
| PA | 21.18 | 21.71 | 21.92 | 21.72 | 21.59 | 21.62 |
| LA | 5.39 | 5.69 | 6.03 | 6.51 | 6.54 | 6.03 |
| Gaussian | PFFT | ±Bernoulli | SRM | |
|---|---|---|---|---|
| BL | 17.65 | 18.35 | 18.14 | 18.17 |
| RA | 10.86 | 11.13 | 10.67 | 10.66 |
| PA | 36.05 | 34.23 | 33.11 | 33.28 |
| LA | 18.44 | 18.71 | 18.14 | 18.61 |
| Gaussian | PFFT | ±Bernoulli | SRM | |
|---|---|---|---|---|
| BL | 27.28 | 25.70 | 26.88 | 26.69 |
| RA | 26.94 | 16.22 | 26.92 | 26.94 |
| PA | 24.63 | 24.22 | 24.38 | 24.24 |
| LA | 27.82 | 26.09 | 27.53 | 27.48 |
| GPSR | OMP | Bayesian | Linear | |
|---|---|---|---|---|
| WH | 7.44 × 104 | -- | -- | -- |
| BL | 9.34 × 104 | 5.57 × 103 | 6.26 × 104 | 114.36 |
| RA | 9.00 × 104 | 5.56 × 103 | 6.64 × 104 | 127.11 |
| PA | 1.14 × 105 | 2.99 × 103 | 7.73 × 104 | 71.97 |
| LA | 5.32 × 105 | 1.70 × 105 | 2.14 × 105 | 3.94 × 103 |
| GPSR | OMP | Bayesian | Linear | |
|---|---|---|---|---|
| WH | 25.08 | -- | -- | -- |
| BL | 22.93 | 23.07 | 24.13 | 28.01 |
| RA | 19.80 | 20.63 | 21.63 | 26.94 |
| PA | 21.03 | 21.61 | 21.57 | 25.44 |
| LA | 23.04 | 23.32 | 24.47 | 28.12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Duan, X.; Li, Y. Measurement Structures of Image Compressive Sensing for Green Internet of Things (IoT). Sensors 2019, 19, 102. https://doi.org/10.3390/s19010102
Li R, Duan X, Li Y. Measurement Structures of Image Compressive Sensing for Green Internet of Things (IoT). Sensors. 2019; 19(1):102. https://doi.org/10.3390/s19010102
Chicago/Turabian StyleLi, Ran, Xiaomeng Duan, and Yanling Li. 2019. "Measurement Structures of Image Compressive Sensing for Green Internet of Things (IoT)" Sensors 19, no. 1: 102. https://doi.org/10.3390/s19010102
APA StyleLi, R., Duan, X., & Li, Y. (2019). Measurement Structures of Image Compressive Sensing for Green Internet of Things (IoT). Sensors, 19(1), 102. https://doi.org/10.3390/s19010102





