Development of Body-Tissue Temperature-Control Transducer
Abstract
:1. Introduction
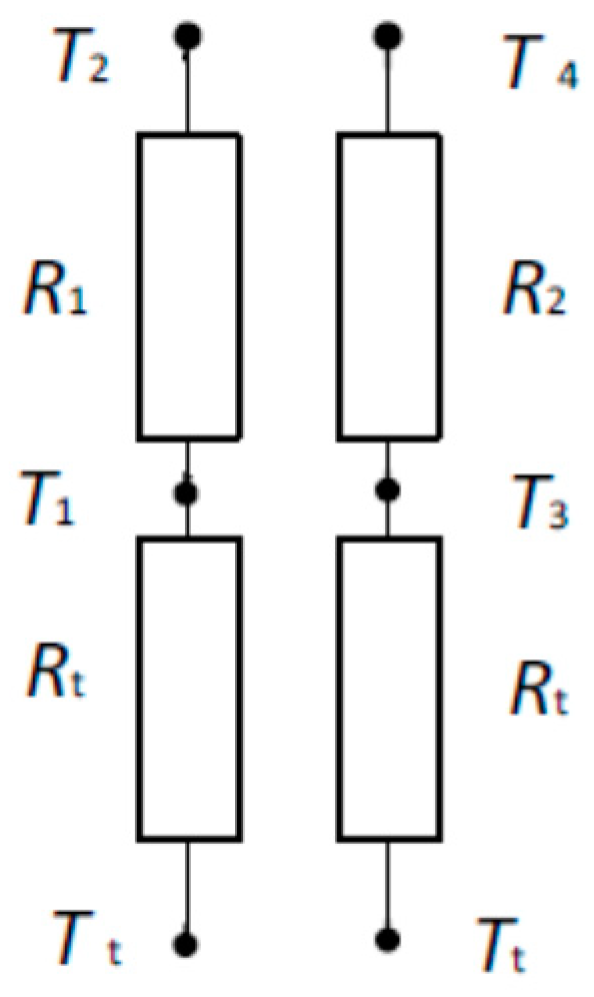
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Mäkinen, M.T.; Pesonen, A.; Jousela, I.; Päivärinta, J.; Poikajärvi, S.; Albäck, A.; Salminen, U.S.; Pesonen, E. Novel Zero-Heat-Flux Deep Body Temperature Measurement in Lower Extremity Vascular and Cardiac Surgery. J. Cardiothorac. Vasc. Anesthesia 2016, 30, 973–978. [Google Scholar] [CrossRef] [PubMed]
- 3M™ Spot On™ Temperature Monitoring System. Available online: https://multimedia.3m.com/mws/media/878163O/spoton-system-brochure.pdf (accessed on 9 October 2018).
- Teunissen, L.P.J.; Klewer, J.; de Haan, A.; de Koning, J.J.; Daanen, A.M. Non-invasive continuous core temperature measurement by zero heat flux. Physiol. Meas. 2011, 32, 559–570. [Google Scholar] [CrossRef] [Green Version]
- Myrer, J.W.; Measom, G.; Durrant, E.; Fellingham, G.W. Cold- and Hot-Pack Contrast Therapy: Subcutaneous and Intramuscular Temperature Change. J. Athletic Train. 1997, 32, 238–241. [Google Scholar]
- Sargeant, A.J. Effect of muscle temperature on leg extension force and short-term power output in humans. Eur. J. Appl. Physiol. 1987, 56, 693–698. [Google Scholar] [CrossRef]
- Tomchuk, D.; Rubley, M.D.; Holcomb, W.R.; Guadagnoli, M.; Tarno, J.M. The magnitude of tissue cooling during cryotherapy with varied types of compression. J. Athletic Train. 2010, 45, 230–237. [Google Scholar] [CrossRef] [PubMed]
- Aadal, L.; Fog, L.; Pedersen, A.R. Tympanic ear thermometer assessment of body temperature among patients with cognitive disturbances. An acceptable and ethically desirable alternative? Scand. J. Caring Sci. 2016, 30, 766–773. [Google Scholar] [CrossRef]
- Erdling, A.; Johansson, A. Core Temperature—The Intraoperative Difference Between Esophageal Versus Nasopharyngeal Temperatures and the Impact of Prewarming, Age, and Weight: A Randomized Clinical Trial. AANA J. 2015, 83, 99–105. [Google Scholar]
- Yeoh, W.K.; Lee, J.K.W.; Lim, H.Y.; Gan, C.W.; Liang, W.; Tan, K.K. Re-visiting the tympanic membrane vicinity as core body temperature measurement site. PLoS ONE 2017, 12, e0174120. [Google Scholar] [CrossRef]
- Flaifel, H.A.N.; Ayoub, F. Esophageal temperature monitoring. Middle East J. Anesth. 2007, 19, 123–147. [Google Scholar]
- Greenes, D.S.; Fleisher, G.R. Accuracy of a Noninvasive Temporal Artery Thermometer for use in Infants. Arch. Pediatr. Adolesc. Med. 2001, 155, 376–381. [Google Scholar] [CrossRef]
- Farnell, S.; Maxwell, L.; Tan, S.; Rhodes, A.; Philips, B. Temperature measurement: Comparison of non-invasive methods used in adult critical care. J. Clin. Nurs. 2005, 14, 632–639. [Google Scholar] [CrossRef] [PubMed]
- Hooper, V.D.; Andrews, J.O. Accuracy of noninvasive core temperature measurement in acutely ill adults: The state of the science. Biol. Res. Nurs. 2006, 8, 24–34. [Google Scholar] [CrossRef] [PubMed]
- Lawson, L.; Bridges, E.J.; Ballou, I.; Greco, S.; Shively, J.; Sochulak, V. Accuracy and precision of noninvasive temperature measurement in adult intensive care patients. Am. J. Crt. Care 2007, 16, 485–496. [Google Scholar]
- Bodkin, R.P.; Aquisto, N.M.; Zwart, J.M.; Toussaint, S.P. Differences in noninvasive thermometer measurements in the adult emergency department. Am. J. Emerg. Med. 2014, 32, 987–989. [Google Scholar] [CrossRef] [PubMed]
- Fogt, D.L.; Henning, A.L.; Venable, A.S.; McFarlin, B.K. Non-invasive Measures of Core Temperature versus Ingestible Thermistor during Exercise in the Heat. Int. J. Exerc. Sci. 2017, 10, 225–233. [Google Scholar] [PubMed]
- Fox, R.H.; Solman, A.J. A new technique for monitoring the deep body temperature in man from the intact skin surface. J. Physiol. 1971, 212, 8–10. [Google Scholar]
- Steck, L.N.; Sparrow, E.M.; Abraham, J.P. Non-invasive measurement of the human core temperature. Int. J. Heat Mass Transfer 2011, 54, 975–982. [Google Scholar] [CrossRef]
- Kimberger, O.; Thell, R.; Schuh, M.; Koch, J.; Sessler, D.I.; Kurz, A. Accuracy and precision of a novel non-invasive core thermometer. Br. J. Anaesthesia 2009, 9, 1–6. [Google Scholar] [CrossRef]
- Gunga, H.C.; Werner, A.; Stahn, A.; Steinach, M.; Schlabs, T.; Koralewski, E.; Kunz, D.; Belavý, D.L.; Felsenberg, D.; Sattler, F.; Koch, J. The Double Sensor-A non-invasive device to continuously monitor core temperature in humans on earth and in space Respir. Physiol. Neurobiol. 2009, 169S, 63–68. [Google Scholar] [CrossRef]
- Uth, M.F.; Koch, J.; Sattler, F. Body Core Temperature Sensing: Challenges and new Sensor Technologies. Procedia Eng. 2016, 168, 89–92. [Google Scholar] [CrossRef]
- Kitamura, K.I.; Zhu, I.; Chen, W.; Nemoto, T. Development of a new method for the noninvasive measurement of deep body temperature without a heater. Med. Eng. Phys. 2010, 32, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Guschlbauer, M.; Maul, A.C.; Yan, X.; Herff, H.; Annecke, T.; Sterner-Kock, A.; Böttiger, B.W.; Schroeder, D.C. Zero-Heat-Flux Thermometry for Non-Invasive Measurement of Core Body Temperature in Pigs. PLoS ONE 2016, 11, e0150759. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, S.; Nakamura, M.; Maeda, E.; Nikawa, Y. Study on Temperature Measurement Using MRI during Acupuncture and Moxibustion. Electron. Commun. Jpn. 2017, 100, 62–67. [Google Scholar] [CrossRef]
- Komiya, H.; Maeda, J.; Suzuki, I. Development of multi-frequency impedance method of measuring muscle temperature noninvasively. Adv. Exerc. Sports Physiol. Date 2014, 15, 1–2. [Google Scholar]
- Buono, M.J.; Jechort, A.; Marques, R.; Smith, C.; Welch, J. Comparison of infrared versus contact thermometry for measuring skin temperature during exercise in the heat. Physiol. Meas. 2007, 28, 855–859. [Google Scholar] [CrossRef] [PubMed]
- Bach, A.J.E.; Stewart, I.B.; Disher, A.E.; Costello, J.T. A comparison between conductive and infrared devices for measuring mean skin temperature at rest, during exercise in the heat, and recovery. PLoS ONE 2015, 10, e0117907. [Google Scholar] [CrossRef] [PubMed]
- 3M™ Bair Hugger™ Temperature Monitoring Patient Sensors, Model 36000. Available online: https://www.3m.com/3M/en_US/company-us/all-3m-products/~/3M-Bair-Hugger-Temperature-Monitoring-Patient-Sensors-Model-36000/?N=5002385+3291653000&rt=rud (accessed on 9 October 2018).
- MacRae, B.A.; Annaheim, S.; Spengler, C.M.; Rossi, R.M. Skin Temperature Measurement Using Contact Thermometry: A Systematic Review of Setup Variables and Their Effects on Measured Values. Front. Physiol. 2018, 9, 1–24. [Google Scholar] [CrossRef]
- Ramanauskiene, I.; Skurvydas, A.; Sipaviciene, S.; Senikiene, Z.; Linonis, V.; Krutulyte, G.; Vizbaraite, D. Influence of heating and cooling on muscle fatigue and recovery. Medicina 2008, 44, 687–693. [Google Scholar] [CrossRef] [PubMed]
- Sipavičienė, S.; Dumčienė, A. Non-invasive muscle temperature control during cooling. Electron. Electr. Eng. 2013, 19, 42–45. [Google Scholar]
- Costello, J.T.; Culligan, K.; Selfe, J.; Donnelly, A.E. Muscle, Skin and Core Temperature after −110 °C Cold Air and 8 °C Water Treatment. PLoS ONE 2012, 7, e48190. [Google Scholar] [CrossRef]
- Jutte, L.S.; Merrick, M.A.; Ingersoll, C.D.; Edwards, J.E. The relationship between intramuscular temperature, skin temperature, and adipose thickness during cryotherapy and rewarming. Arch. Phys. Med. Rehabil. 2001, 82, 845–850. [Google Scholar] [CrossRef] [PubMed]
- Akgun, K.; Korpinar, M.A.; Kalkan, M.T.; Akarirmak, U.; Tuzun, S.; Tuzun, F. Temperature changes in superficial and deep tissue layers with respect to time of cold pack application in dogs. Yonsei Med. J. 2004, 45, 711–718. [Google Scholar] [CrossRef] [PubMed]
- Merrick, M.A.; Knight, K.L.; Ingersoll, C.D.; Potteiger, J.A. The Effects of Ice and Compression Wraps on Intramuscular Temperatures at Various Depths. J. Athletic Train. 1993, 28, 236–245. [Google Scholar]
- Merrick, M.A.; Jutte, L.S.; Smith, M.E. Cold Modalities with Different Thermodynamic Properties Produce Different Surface and Intramuscular Temperatures. J. Athletic Train. 2003, 38, 28–33. [Google Scholar]
- Dykstra, J.H.; Hill, H.M.; Miller, M.G.; Cheatham, C.C.; Michael, T.J.; Baker, R.J. Comparisons of Cubed Ice, Crushed Ice, and Wetted Ice on Intramuscular and Surface Temperature Changes. J. Athletic Train. 2009, 44, 136–141. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, D.; Ebbini, E.S. Real-Time 2-D Temperature Imaging Using Ultrasound. IEEE Trans. Biomed. Eng. 2010, 57, 12–16. [Google Scholar] [PubMed] [Green Version]
- Stauffer, P.R.; Snow, B.W.; Rodrigues, D.B.; Salahi, S.; Oliveira, T.G.; Reudink, D.; Maccarini, P.F. Non-Invasive Measurement of Brain Temperature with Microwave Radiometry: Demonstration in a Head Phantom and Clinical Case. Neuroradiol. J. 2014, 27, 3–12. [Google Scholar] [CrossRef] [Green Version]
- Laxminarayan, S.; Rakesh, V.; Oyama, T.; Kazman, J.B.; Yanovich, R.; Ketko, I.; Epstein, Y.; Morrison, S.; Reifman, J. Individualized estimation of human core body temperature using noninvasive measurements. J. Appl. Physiol. 2018, 124, 1387–1402. [Google Scholar] [CrossRef]
- Buller, M.J.; Tharion, W.J.; Cheuvront, S.N.; Montain, S.J.; Kenefick, R.W.; Castellani, J.; Latzka, W.A.; Roberts, W.S.; Richter, M.; Jenkins, O.C.; et al. Estimation of human core temperature from sequential heart rate observations. Physiol. Meas. 2013, 34, 781–798. [Google Scholar] [CrossRef]
- Potter, A.W.; Blanchard, L.; Friedl, K.E.; Cadarette, B.S.; Hoyt, R.W. Mathematical prediction of core body temperature from environment, activity, and clothing: The heat strain decision aid (HSDA). J. Therm. Biol. 2017, 64, 78–85. [Google Scholar] [CrossRef]
- Imani, F.; Rouzbahani, H.R.K.; Goudarzi, M.; Tarrahi, M.J.; Soltani, A.E. Skin Temperature Over the Carotid Artery, an Accurate Non-invasive Estimation of Near Core Temperature. Anesthesiol. Pain Med. 2016, 6, E31046. [Google Scholar] [CrossRef] [PubMed]
- Augustine, G.; Augustine, S. Accurate Non-Invasive Temperature Monitoring Device. In Proceedings of the 2017 Design of Medical Devices Conference DMD2017, Minneapolis, MN, USA, 10–13 April 2017. [Google Scholar]
- Chung, S.H.; Mehta, M.; Tromberg, B.J.; Yodh, A.G. Non-invasive measurement of deep tissue temperature changes caused by apoptosis during breast cancer neoadjuvant chemotherapy: A case study. J. Innov. Opt. Health Sci. 2011, 4, 361–372. [Google Scholar] [CrossRef] [PubMed]
- Pouch, A.M.; Cary, T.W.; Schultz, S.M.; Sehgal, C.M. In Vivo Noninvasive Temperature Measurement by B-Mode Ultrasound Imaging. J. Ultrasound. Med. 2010, 29, 1595–1606. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Feng, X.; Ruochong, Z.; Zheng, Y. Portable photoacoustic system for noninvasive blood temperature measurement. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Dumciene, A.; Sipaviciene, S. Deeper-Layer Body Tissue Temperature Control Using Multi-Sensory Transducer. Elektronika ir Elektrotechnika 2015, 21, 24–27. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperature in the Resting Human Forearm. J. Appl. Physiol. 1948, 1, 93–102. [Google Scholar] [CrossRef]
- Lakhssassi, A.; Kengne, E.; Semmaoui, H. Modifed pennes’ equation modelling bio-heat transfer in living tissues: Analytical and numerical analysis. Nat. Sci. 2010, 2, 1375–1385. [Google Scholar] [CrossRef]
- Katić, K.; Li, R.; Zeiler, W. Thermophysiological models and their applications: A review. Build. Environ. 2016, 106, 286–300. [Google Scholar] [CrossRef]
- Coccarelli, A.; Boileau, E.; Parthimos, D.; Nithiarasu, P. An advanced computational bioheat transfer model for a human body with an embedded systemic circulation. Biomech. Model Mechanobiol. 2016, 15, 1173–1190. [Google Scholar] [CrossRef]
- McIntosh, R.L.; Anderson, V. A comprehensive tissue properties database provided for the thermal assessment of a human at rest. Biophys. Rev. Lett. 2001, 5, 129–151. [Google Scholar] [CrossRef]
- Eston, R.; Peters, D. Effect of cold water immersion on the symptoms of exercise-induced muscle damage. J. Sports Sci. 1999, 17, 231–238. [Google Scholar] [CrossRef]
- Mars, M.; Hadebe, B.; Tufts, M. The effect of icepack cooling on skin and muscle temperature at rest and after exercise. S. Afr. J. Sports Med. 2006, 18, 60–66. [Google Scholar] [CrossRef]
- Psikuta, A.; Niedermann, R.; Rossi, R.M. Effect of ambient temperature and attachment method on surface temperature measurements. Int. J. Biometeorol. 2014, 58, 877–885. [Google Scholar] [CrossRef] [PubMed]
- MacRae, B.A.; Annaheim, S.; Stämpfli, R.; Spengler, C.M.; Rossi, R.M. Validity of contact skin temperature sensors under different environmental conditions with and without fabric coverage: Characterisation and correction. Int. J. Biometeorol. 2018, 62, 1861–1872. [Google Scholar] [CrossRef] [PubMed]
- Brazaitis, M.; Eimantas, N.; Daniuseviciute, L.; Mickeviciene, D.; Steponaviciute, R.; Skurvydas, A. Two Strategies for Response to 14 °C Cold-Water Immersion: Is there a Difference in the Response of Motor, Cognitive, Immune and Stress Markers? PLoS ONE 2014, 9, e109020. [Google Scholar] [CrossRef] [PubMed]







| Layer | ρ (kg/m3) | k (W/m*K) | Cp (J/kg*K) | Thickness (m) | Qm (W/m3) | ωb (1/s) | Tb (K) |
|---|---|---|---|---|---|---|---|
| Muscle | 1090 | 0.5 | 3766 | 0.12 | 5 | 0.0001 | 310.15 |
| Fat | 850 | 0.16 | 2510 | 0.0025 | 0 | 4/5E−6 | 310.15 |
| Skin | 1100 | 0.21 | 3250 | 0.002 | 4 | 7.2E−8 | 310.15 |
| Blood | 1050 | 0.32 | 1313 | 0.03 | 0.5 | 310.15 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumciene, A.; Sipaviciene, S. Development of Body-Tissue Temperature-Control Transducer. Sensors 2019, 19, 14. https://doi.org/10.3390/s19010014
Dumciene A, Sipaviciene S. Development of Body-Tissue Temperature-Control Transducer. Sensors. 2019; 19(1):14. https://doi.org/10.3390/s19010014
Chicago/Turabian StyleDumciene, Audrone, and Saule Sipaviciene. 2019. "Development of Body-Tissue Temperature-Control Transducer" Sensors 19, no. 1: 14. https://doi.org/10.3390/s19010014
APA StyleDumciene, A., & Sipaviciene, S. (2019). Development of Body-Tissue Temperature-Control Transducer. Sensors, 19(1), 14. https://doi.org/10.3390/s19010014





