Figure 1.
A driver performs a hand gesture in the detection range of time-of-flight (ToF) sensors (red area). This in-car setup uses a mobile tablet computer and two ToF sensors to recognise hand gestures in order to control an infotainment device.
Figure 1.
A driver performs a hand gesture in the detection range of time-of-flight (ToF) sensors (red area). This in-car setup uses a mobile tablet computer and two ToF sensors to recognise hand gestures in order to control an infotainment device.
Figure 2.
Dynamic hand gesture recognition flowchart from [
5].
Figure 2.
Dynamic hand gesture recognition flowchart from [
5].
Figure 3.
The recurrent three-dimensional convolutional architecture from [
23]. As input, the network uses a dynamic gesture in the form of successive frames. It extracts local spatio-temporal features via a 3D Convolutional Neural Network (CNN) and feeds those into a recurrent layer, which aggregates activation across the sequence. Using these activations, a softmax layer then outputs probabilities for the dynamic gesture class.
Figure 3.
The recurrent three-dimensional convolutional architecture from [
23]. As input, the network uses a dynamic gesture in the form of successive frames. It extracts local spatio-temporal features via a 3D Convolutional Neural Network (CNN) and feeds those into a recurrent layer, which aggregates activation across the sequence. Using these activations, a softmax layer then outputs probabilities for the dynamic gesture class.
Figure 4.
The FOANet architecture [
24], which consists of a separate channel for every focus region (global, left hand, right hand) and input modality (RGB, depth, RGB flow and depth flow).
Figure 4.
The FOANet architecture [
24], which consists of a separate channel for every focus region (global, left hand, right hand) and input modality (RGB, depth, RGB flow and depth flow).
Figure 5.
The timeline consolidates some but not all important contributions in the field of hand gesture recognition with depth data. On the right-hand side, we name the important contributions of our own line of research; on the left-hand side, we show the most relevant studies from other research teams.
Figure 5.
The timeline consolidates some but not all important contributions in the field of hand gesture recognition with depth data. On the right-hand side, we name the important contributions of our own line of research; on the left-hand side, we show the most relevant studies from other research teams.
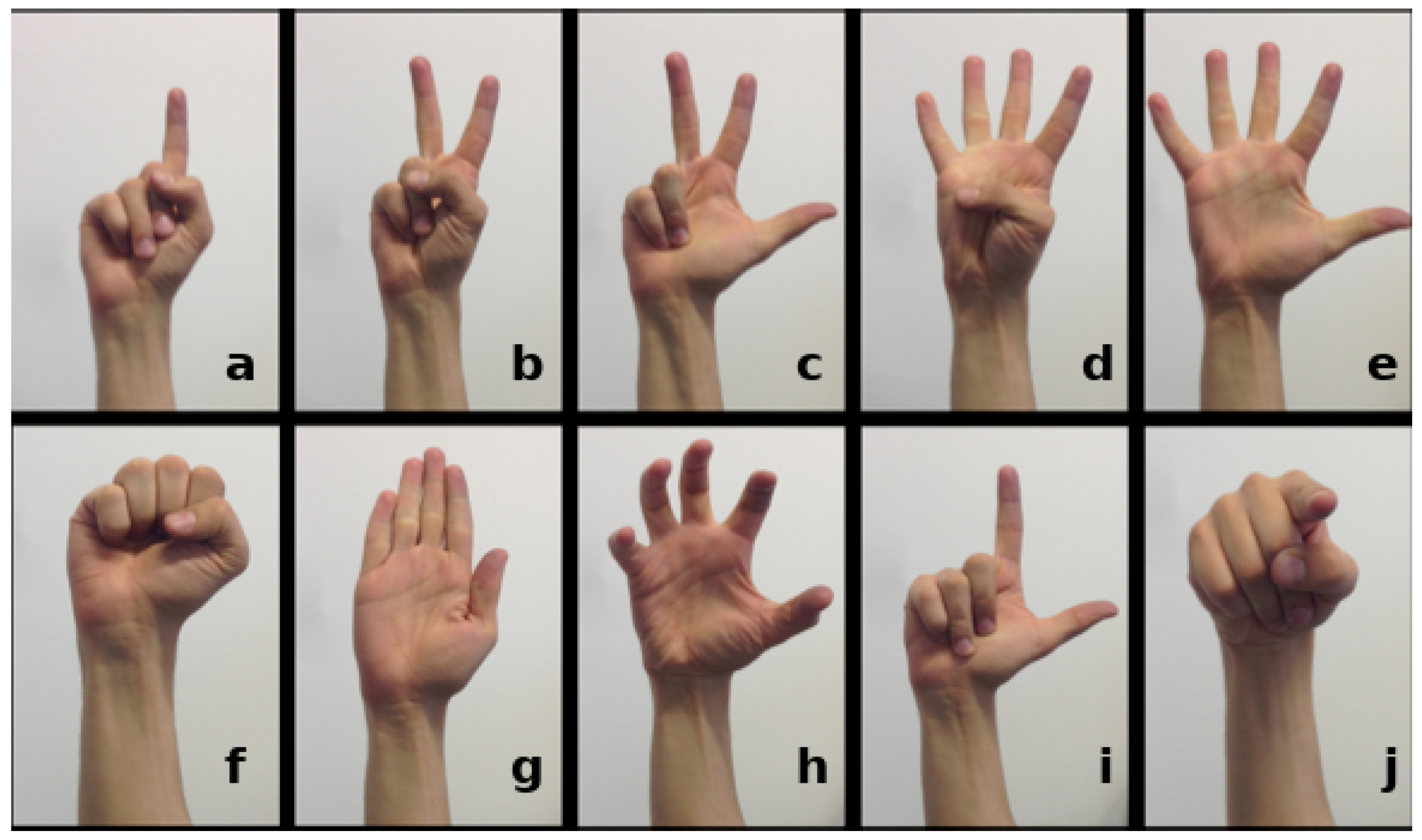
Figure 6.
The set of ten hand posture classed (
a–
j) that we used throughout our research and provided samples from in our REHAP if appropriate benchmark dataset [
34]. The hand poses in the top row raise different numbers of fingers, indicating a certain numerical value. The classes in the bottom row feature other meaningful postures like a fist, a flat hand, a grip, an L-shape and finger pointing, which form some elements for dynamic hand gestures.
Figure 6.
The set of ten hand posture classed (
a–
j) that we used throughout our research and provided samples from in our REHAP if appropriate benchmark dataset [
34]. The hand poses in the top row raise different numbers of fingers, indicating a certain numerical value. The classes in the bottom row feature other meaningful postures like a fist, a flat hand, a grip, an L-shape and finger pointing, which form some elements for dynamic hand gestures.
Figure 7.
A setup for recording hand gestures with a Camboard Nano sensor. We divide the detection area into three zones: near (15–30 cm), intermediate (30–45 cm) and far (45–60 cm).
Figure 7.
A setup for recording hand gestures with a Camboard Nano sensor. We divide the detection area into three zones: near (15–30 cm), intermediate (30–45 cm) and far (45–60 cm).
Figure 8.
A raw three-dimensional point cloud of a grip-like gesture. (left and right column): the same gesture from different points of view; (top row and bottom row): the same gesture a few frames later.
Figure 8.
A raw three-dimensional point cloud of a grip-like gesture. (left and right column): the same gesture from different points of view; (top row and bottom row): the same gesture a few frames later.
Figure 9.
A demonstration of our preprocessing method. After applying a depth threshold and Principal Component Analysis (PCA), the green voxels (left) remain for further processing and serve to identify the correct hand posture class (right).
Figure 9.
A demonstration of our preprocessing method. After applying a depth threshold and Principal Component Analysis (PCA), the green voxels (left) remain for further processing and serve to identify the correct hand posture class (right).
Figure 10.
Principal component analysis of a raw hand posture point cloud (left) effectively performs cropping to the essential hand parts (right), which contains the most relevant information for hand posture classification.
Figure 10.
Principal component analysis of a raw hand posture point cloud (left) effectively performs cropping to the essential hand parts (right), which contains the most relevant information for hand posture classification.
Figure 11.
Support vector machine grid search landscape for Radial Basis Function (RBF) kernel parameters subject to the Viewpoint Feature Histogram (VFH) descriptor. For an increasing penalty factor C, the kernel parameter decreases in significance.
Figure 11.
Support vector machine grid search landscape for Radial Basis Function (RBF) kernel parameters subject to the Viewpoint Feature Histogram (VFH) descriptor. For an increasing penalty factor C, the kernel parameter decreases in significance.
Figure 12.
Classification rates for in the range of for different descriptors and confidence measures using an MLP. The first row shows the VFH descriptor accuracies for ToF sensors in an angle of 30°, respectively in an angle of 90° for the second row. The third row concerns the ESF descriptor for an angle of 30° between the two sensors. From left to right, the first two columns show the performance when using only the first or second ToF sensor; the third column represents the late fusion approach and the fourth column the early fusion approach.
Figure 12.
Classification rates for in the range of for different descriptors and confidence measures using an MLP. The first row shows the VFH descriptor accuracies for ToF sensors in an angle of 30°, respectively in an angle of 90° for the second row. The third row concerns the ESF descriptor for an angle of 30° between the two sensors. From left to right, the first two columns show the performance when using only the first or second ToF sensor; the third column represents the late fusion approach and the fourth column the early fusion approach.
Figure 13.
A sketch of our two-stage MLP model (top) and an affiliated training procedure (bottom). For an input histogram of size and an output layer size of neurons, the secondary MLP receives the primary MLPs’ output activation plus another histogram as input. In our training procedure, we split our dataset D in three parts , and , such that we may train our two MLPs on independent parts of the dataset and test it on unseen data.
Figure 13.
A sketch of our two-stage MLP model (top) and an affiliated training procedure (bottom). For an input histogram of size and an output layer size of neurons, the secondary MLP receives the primary MLPs’ output activation plus another histogram as input. In our training procedure, we split our dataset D in three parts , and , such that we may train our two MLPs on independent parts of the dataset and test it on unseen data.
Figure 14.
An exemplary hand gesture recognition setup. A user performs a dynamic gesture defined by a starting pose and an ending pose. For a dynamic grabbing gesture, pose class
(grab) starts the sequence which
(fist) ends. See
Figure 6 for an overview of our ten hand pose classes. Our machine learning systems recognise the individual poses and an algorithm on top tries to identify the sequence.
Figure 14.
An exemplary hand gesture recognition setup. A user performs a dynamic gesture defined by a starting pose and an ending pose. For a dynamic grabbing gesture, pose class
(grab) starts the sequence which
(fist) ends. See
Figure 6 for an overview of our ten hand pose classes. Our machine learning systems recognise the individual poses and an algorithm on top tries to identify the sequence.
Figure 15.
The structure of our CNN model. The first convolution step followed by a reshape (top row) yields input for the second convolution step, followed by a max-pooling layer (middle row), whose activation provides input for an MLP with 100 hidden neurons and 10 output neurons, one per hand pose class (bottom row).
Figure 15.
The structure of our CNN model. The first convolution step followed by a reshape (top row) yields input for the second convolution step, followed by a max-pooling layer (middle row), whose activation provides input for an MLP with 100 hidden neurons and 10 output neurons, one per hand pose class (bottom row).
Figure 16.
Resulting filter activations for the 20 kernels in the first layer of our CNN model from
Figure 15. This figure shows the filtered activation for each hand gesture, grouped as in
Figure 6.
Figure 16.
Resulting filter activations for the 20 kernels in the first layer of our CNN model from
Figure 15. This figure shows the filtered activation for each hand gesture, grouped as in
Figure 6.
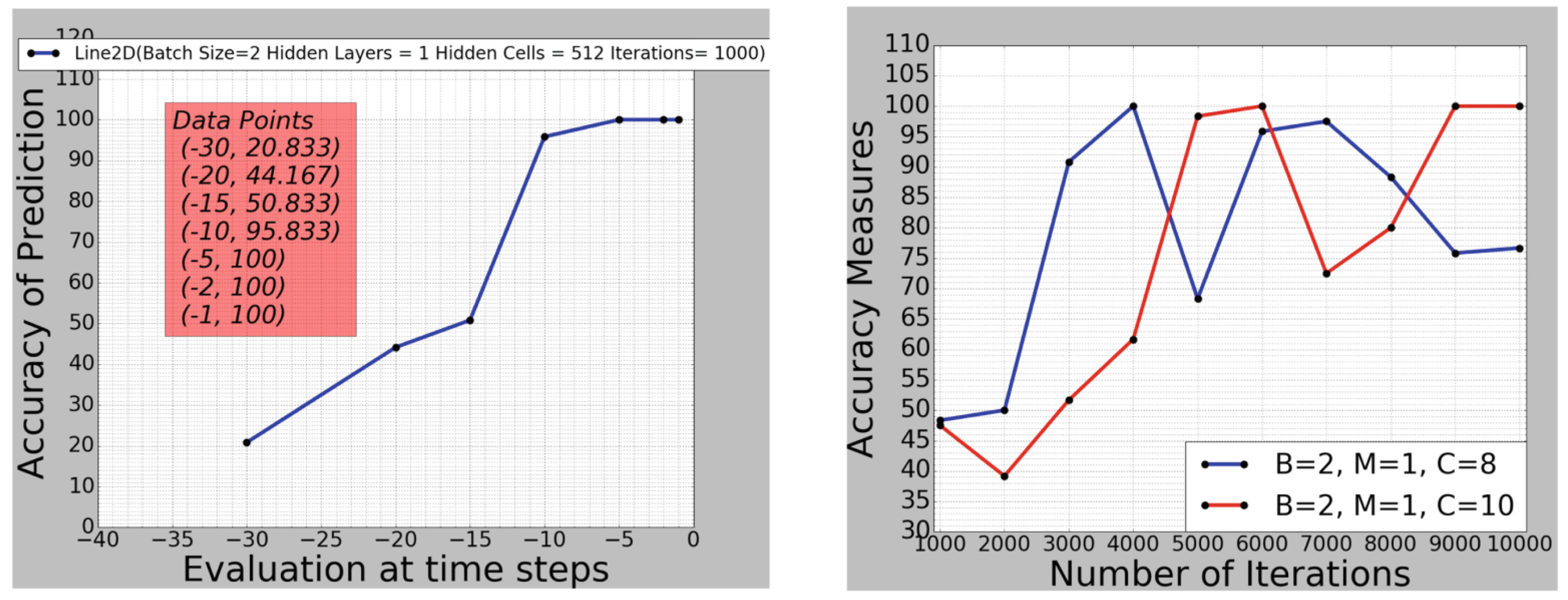
Figure 17.
(left): accuracy of LSTM prediction on a single test data sample, with , , and , at different in-gesture time steps t; (right): accuracy of prediction taken at the end of a gesture, depending on training iterations for a small LSTM network size.
Figure 17.
(left): accuracy of LSTM prediction on a single test data sample, with , , and , at different in-gesture time steps t; (right): accuracy of prediction taken at the end of a gesture, depending on training iterations for a small LSTM network size.
Figure 18.
Sample screens of a dummy interface design used in our usability studies. The user may not address all functions via hand gestures but may navigate through the menus (social contacts, street maps, phone calls and in-car climate control) with gestures
a to
e from
Figure 6 as well as start/stop (gesture
g,
j). In later versions, we also implemented controls for zooming.
Figure 18.
Sample screens of a dummy interface design used in our usability studies. The user may not address all functions via hand gestures but may navigate through the menus (social contacts, street maps, phone calls and in-car climate control) with gestures
a to
e from
Figure 6 as well as start/stop (gesture
g,
j). In later versions, we also implemented controls for zooming.
Figure 19.
The procedure of our human–machine interaction experiment in three phases. Participants interacting with an in-car infotainment device start with a free exploration and later receive instructions on how to actually use the system.
Figure 19.
The procedure of our human–machine interaction experiment in three phases. Participants interacting with an in-car infotainment device start with a free exploration and later receive instructions on how to actually use the system.
Figure 20.
A participant performs the Lane Change Test while controlling the infotainment system via mid-air hand gestures.
Figure 20.
A participant performs the Lane Change Test while controlling the infotainment system via mid-air hand gestures.
Figure 21.
(left): Lane Change Tests results for the nine participants in group T (top) and the eight participants in Group M (bottom) in terms of mean deviation from the baseline, (right): an exemplary Lane Change Test track. The green line (baseline) shows the optimal course, the red line the trajectory actually driven by the participant. A trial lasts for approximately three minutes and contains a total of 18 lane change signs.
Figure 21.
(left): Lane Change Tests results for the nine participants in group T (top) and the eight participants in Group M (bottom) in terms of mean deviation from the baseline, (right): an exemplary Lane Change Test track. The green line (baseline) shows the optimal course, the red line the trajectory actually driven by the participant. A trial lasts for approximately three minutes and contains a total of 18 lane change signs.
Table 1.
Overall results of FOANet and compared architectures on the Nvidia benchmark.
Table 1.
Overall results of FOANet and compared architectures on the Nvidia benchmark.
| Method | Channels | Accuracy |
|---|
| FOANet | FOA + Sparse Fusion | 91.28% |
| FOANet | FOA + Avg. Fusion | 85.26% |
| Human | Colour | 88.4% |
| Molchanov [23] | All (including infrared) | 83.8% |
| Molchanov [23] | Depth + Flow | 82.4% |
Table 2.
Individual channel performances of FOANet on the Nvidia benchmark.
Table 2.
Individual channel performances of FOANet on the Nvidia benchmark.
| RGB | Depth | RGB Flow | Depth Flow |
|---|
| Global | 43.98% | 66.80% | 62.66% | 58.71% |
| Focus | 58.09% | 73.65% | 77.18% | 70.12% |
Table 3.
Support Vector Machine (SVM) classification accuracies for both kernel types, the ESF and VFH descriptors and two camera set ups in an angle of 30° respectively 90°.
Table 3.
Support Vector Machine (SVM) classification accuracies for both kernel types, the ESF and VFH descriptors and two camera set ups in an angle of 30° respectively 90°.
| Descriptor | ESF 30° | ESF 90° | VFH 30° | VFH 90° |
|---|
| Classif. rate scalar kernel | 98.7% | 98.8% | 96.9% | 94.2% |
| Classif. rate gauss kernel | 99.8% | 99.6% | 98.8% | 93.1% |
Table 4.
The impact of an increasing (top row) on the average classification error (middle row) and the number of rejected samples (bottom row), averaged over 100,000 samples.
Table 4.
The impact of an increasing (top row) on the average classification error (middle row) and the number of rejected samples (bottom row), averaged over 100,000 samples.
| θconf | 0 | 0.65 | 0.95 |
|---|
| Avg. Error | 6.3% | 3.6% | 1.3% |
| rejected samples | 0 | 6776 | 34005 |
Table 5.
The average change in classification accuracy for each of our ten hand gesture classes when using the two-stage model. Some but not all classes improve reasonably well, while class d seems to suffer in terms of recognition accuracy.
Table 5.
The average change in classification accuracy for each of our ten hand gesture classes when using the two-stage model. Some but not all classes improve reasonably well, while class d seems to suffer in terms of recognition accuracy.
| a | b | c | d | e | f | g | h | i | j |
|---|
| +0.01 | +0.02 | +0.01 | −0.03 | +0.07 | +0.01 | +0.05 | +0.04 | +0.01 | +0.04 |
Table 6.
Generalisation performance comparison of the primary Multilayer Perceptron (MLP) (upper row) and the secondary MLP (lower row) using the training procedure depicted in
Figure 13.
Table 6.
Generalisation performance comparison of the primary Multilayer Perceptron (MLP) (upper row) and the secondary MLP (lower row) using the training procedure depicted in
Figure 13.
| a | b | c | d | e | f | g | h | i | j |
|---|
| MLP1 | 90% | 90% | 89% | 87% | 87% | 95% | 92% | 92% | 89% | 95% |
| MLP2 | 93% | 93% | 93% | 90% | 91% | 97% | 94% | 94% | 91% | 96% |
Table 7.
Generalisation results for all 16 persons and both MLPs, each with 30 and 50 neurons, respectively. Here, column 1 represents the performance of our four MLPs, trained on persons 2 to 16 and tested on person 1.
Table 7.
Generalisation results for all 16 persons and both MLPs, each with 30 and 50 neurons, respectively. Here, column 1 represents the performance of our four MLPs, trained on persons 2 to 16 and tested on person 1.
| Participant | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Acc. |
|---|
| MLP1-30 | 81% | 50% | 69% | 55% | 76% | 59% | 56% | 68% | 79% | 68% | 88% | 72% | 95% | 72% | 87% | 79% | 72.1% |
| MLP2-30 | 83% | 51% | 72% | 60% | 79% | 62% | 58% | 72% | 85% | 74% | 89% | 73% | 97% | 75% | 91% | 83% | 75.3% |
| MLP1-50 | 83% | 49% | 69% | 58% | 79% | 62% | 57% | 68% | 84% | 70% | 89% | 75% | 90% | 74% | 90% | 80% | 74.0% |
| MLP2-50 | 86% | 52% | 74% | 63% | 83% | 65% | 60% | 72% | 89% | 74% | 90% | 75% | 98% | 75% | 93% | 82% | 77.0% |
Table 8.
Every participant performed each hand gesture ten times. An entry names the number of correctly recognised samples.
Table 8.
Every participant performed each hand gesture ten times. An entry names the number of correctly recognised samples.
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 |
|---|
| grab | 10 | 6 | 3 | 5 | 5 | 8 | 6 | 7 | 5 | 4 |
| release | 7 | 6 | 9 | 8 | 9 | 8 | 8 | 9 | 9 | 7 |
| zoom in | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| zoom out | 9 | 10 | 7 | 10 | 9 | 9 | 10 | 8 | 9 | 9 |
Table 9.
Test results of three investigated CNN models on a total of four different datasets in terms of classification error.
Table 9.
Test results of three investigated CNN models on a total of four different datasets in terms of classification error.
| W150 | W100 + 50 | ROTARM | REHAP |
|---|
| CNN-2DP | 36.1% | 41.8% | 62.0% | 16.1% |
| CNN-PPC | 17.5% | 27.4% | 55.6% | 16.5% |
| CNN-NPC | 39.5% | 40.2% | 73.3% | 25.2% |
Table 10.
The five best results from our Convolutional Neural Network (CNN) parameter grid search in terms of classification error (CE).
Table 10.
The five best results from our Convolutional Neural Network (CNN) parameter grid search in terms of classification error (CE).
| Result Rank | | | | | | CE |
|---|
| 1 | 20 | 30 | 3 | 6 | 1 | 5.557 |
| 2 | 20 | 20 | 3 | 4 | 1 | 5.957 |
| 3 | 20 | 25 | 3 | 6 | 1 | 5.971 |
| 4 | 20 | 35 | 3 | 6 | 1 | 5.971 |
| 5 | 20 | 35 | 3 | 7 | 1 | 5.985 |
Table 11.
The best 18 results of our long short-term memory (LSTM) parameter grid search. We conducted a total of 108 experiments, varying the network topology and training parameters.
Table 11.
The best 18 results of our long short-term memory (LSTM) parameter grid search. We conducted a total of 108 experiments, varying the network topology and training parameters.
| B | 2 | 5 | 10 | 10 | 5 | 2 | 10 | 5 | 5 | 10 | 10 | 5 | 2 | 5 | 2 | 5 | 5 | 2 |
|---|
| M | 1 | 1 | 4 | 3 | 2 | 1 | 3 | 2 | 4 | 1 | 2 | 1 | 4 | 4 | 2 | 4 | 2 | 1 |
| C | 512 | 256 | 128 | 512 | 128 | 256 | 256 | 512 | 128 | 128 | 128 | 512 | 128 | 512 | 512 | 256 | 128 | 128 |
| I | 104 | 104 | 5 × 103 | 5 × 103 | 5 × 103 | 104 | 5 × 103 | 104 | 104 | 5 × 103 | 104 | 104 | 104 | 5 × 103 | 104 | 104 | 104 | 104 |
| 100 | 96.7 | 100 | 98.3 | 100 | 95 | 96.7 | 96.7 | 100 | 97.5 | 99.2 | 100 | 100 | 99.2 | 100 | 100 | 95.8 | 96.7 |
Table 12.
Summary of the performances of the methods we investigated in our course of research.
Table 12.
Summary of the performances of the methods we investigated in our course of research.
| Method | Data Samples (Train/Test) | Training Performance | Test Performance |
|---|
| MLP | 100,000/100,000 | 93.7% | 98.7% |
| SVM | 160,000/160,000 | N/A | 99.8% |
| Two-stage MLP | 160,000/160,000/160,000 | 97% | 77% |
| CNN | 266,000/114,000 | 94.5% | 98.5% |
| LSTM | 480/120 | 100% | 100% |
Table 13.
Selected INTUI questionnaire scores from our human–machine interaction experiment.
Table 13.
Selected INTUI questionnaire scores from our human–machine interaction experiment.
| Mean | Standard Deviation |
|---|
| Effortlessness | 3.98 | 0.93 |
| Gut feeling | 2.65 | 1.15 |
| Verbalisation | 6.967 | 0.01 |
| Magic experience | 4.85 | 0.79 |
| Intuition | 3.2 | 1.9 |