RGBD-Inertial Trajectory Estimation and Mapping for Ground Robots
Abstract
:1. Introduction
- Formulation and implementation of a depth-integrated initialization process for the VINS-RGBD system.
- Formulation and implementation of a depth-integrated Visual Inertial Odometry (VIO), overcoming the degenerated cases of a vision and IMU only VIO system.
- Design and implementation of a backend mapping function to build dense point clouds with noise suppression, which is suitable for further map post processing and path planning.
- A color-depth-inertial dataset with handheld, wheeled robot, and tracked robot motion, with tracking system data for ground truth poses.
- Thorough evaluation of the proposed VINS-RGBD system using the three datasets mentioned above.
2. Related Work
3. VINS-Mono Analysis
3.1. Vision Front End
3.2. IMU Pre-Integration
3.3. Visual-Inertial Initialization and VIO
3.3.1. Visual-Inertial Initialization
3.3.2. Visual-Inertial Odometry
3.4. Loop Detection and Pose Graph Optimization
3.5. Observability Analysis of VINS-Mono
4. VINS-RGBD
4.1. Depth Estimation
4.2. System Initialization
4.3. Depth-Integrated VIO
| Algorithm 1: Depth verification algorithm. |
 |
4.4. Loop Closing
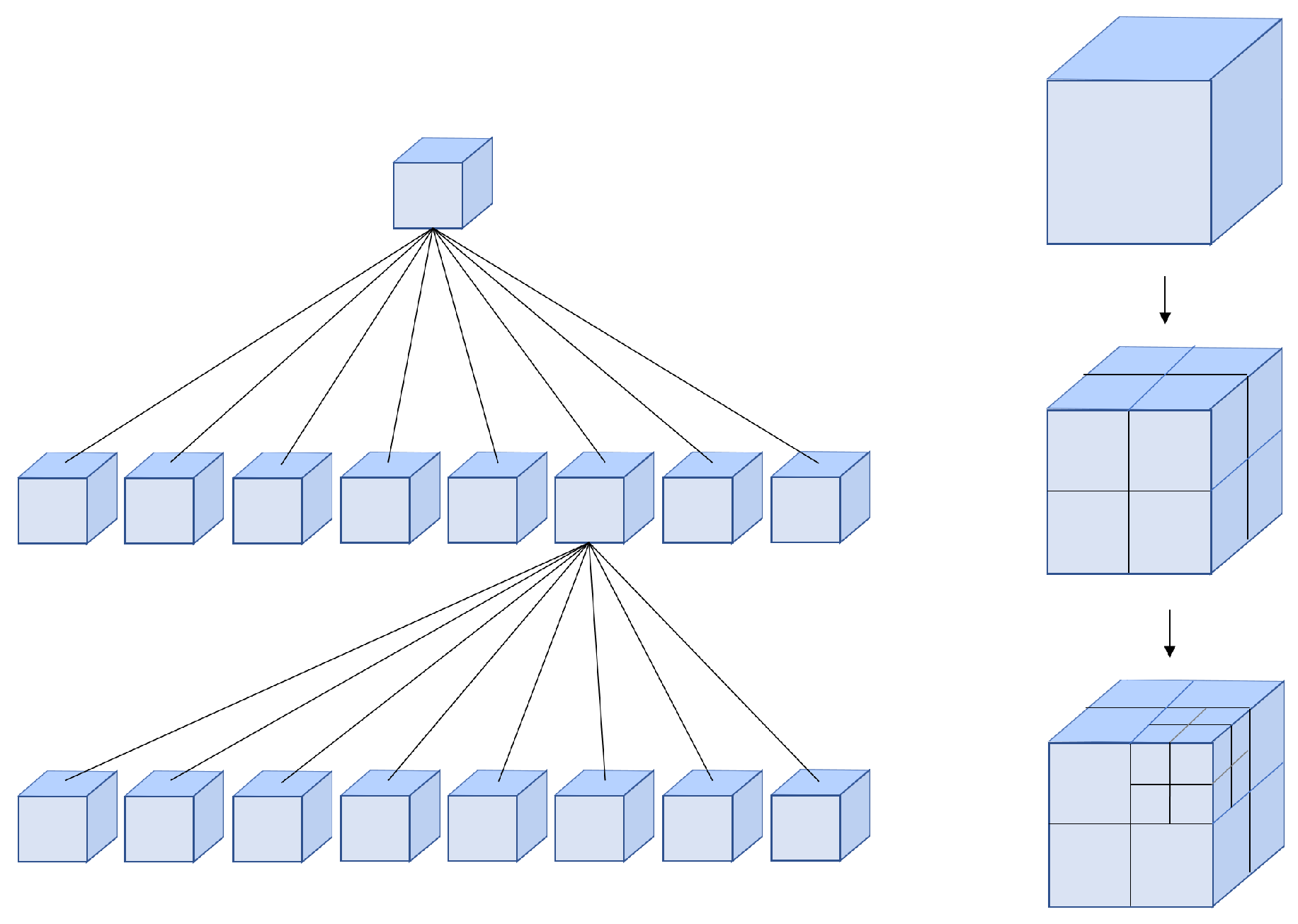
4.5. Mapping and Noise Elimination
5. Experiments and Results
5.1. Scale Drift Experiment
5.2. Open Outdoor Experiment
5.3. Integrated Experiments
5.3.1. Handheld and Wheeled Experiment
5.3.2. Tracked Experiment
5.4. Map Comparison
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bloss, R. Sensor innovations helping unmanned vehicles rapidly growing smarter, smaller, more autonomous and more powerful for navigation, mapping, and target sensing. Sens. Rev. 2015, 35, 6–9. [Google Scholar] [CrossRef]
- Bloss, R. Unmanned vehicles while becoming smaller and smarter are addressing new applications in medical, agriculture, in addition to military and security. Ind. Robot 2014, 41, 82–86. [Google Scholar] [CrossRef]
- Birk, A.; Schwertfeger, S.; Pathak, K. A networking framework for teleoperation in safety, security, and rescue robotics. IEEE Wirel. Commun. 2009, 16, 6–13. [Google Scholar] [CrossRef]
- Colas, F.; Mahesh, S.; Pomerleau, F.; Liu, M.; Siegwart, R. 3D path planning and execution for search and rescue ground robots. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 722–727. [Google Scholar]
- Pathak, K.; Birk, A.; Schwertfeger, S.; Delchef, I.; Markov, S. Fully autonomous operations of a jacobs rugbot in the robocup rescue robot league 2006. In Proceedings of the IEEE International Workshop on Safety, Security and Rescue Robotics, Rome, Italy, 27–29 September 2007; pp. 1–6. [Google Scholar]
- Thrun, S.; Thayer, S.; Whittaker, W.; Baker, C.; Burgard, W.; Ferguson, D.; Hahnel, D.; Montemerlo, D.; Morris, A.; Omohundro, Z.; et al. Autonomous exploration and mapping of abandoned mines. IEEE Robot. Autom. Mag. 2004, 11, 79–91. [Google Scholar] [CrossRef] [Green Version]
- Grisetti, G.; Stachniss, C.; Burgard, W. Improved techniques for grid mapping with rao-blackwellized particle filters. IEEE Trans. Robot. 2007, 23, 34. [Google Scholar] [CrossRef]
- Birk, A.; Vaskevicius, N.; Pathak, K.; Schwertfeger, S.; Poppinga, J.; Buelow, H. 3-D perception and modeling. IEEE Robot. Autom. Mag. 2009, 16, 53–60. [Google Scholar] [CrossRef]
- Kohlbrecher, S.; Von Stryk, O.; Meyer, J.; Klingauf, U. A flexible and scalable slam system with full 3d motion estimation. In Proceedings of the IEEE International Symposium on Safety, Security, and Rescue Robotics, Kyoto, Japan, 1–5 November 2011; pp. 155–160. [Google Scholar]
- Davison, A.J. Real-time simultaneous localisation and mapping with a single camera. In Proceedings of the ICCV 2003, Nice, France, 13–16 October 2003; Volume 3, pp. 1403–1410. [Google Scholar]
- Huang, G.P.; Mourikis, A.I.; Roumeliotis, S.I. Analysis and improvement of the consistency of extended Kalman filter based SLAM. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 473–479. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Endres, F.; Hess, J.; Sturm, J.; Cremers, D.; Burgard, W. 3-D mapping with an RGB-D camera. IEEE Trans. Robot. 2014, 30, 177–187. [Google Scholar] [CrossRef]
- Newcombe, R.A.; Izadi, S.; Hilliges, O.; Molyneaux, D.; Kim, D.; Davison, A.J.; Kohi, P.; Shotton, J.; Hodges, S.; Fitzgibbon, A. KinectFusion: Real-time dense surface mapping and tracking. In Proceedings of the IEEE International Symposium on Mixed and Augmented Reality, Basel, Switzerland, 26–29 October 2011; pp. 127–136. [Google Scholar]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Li, M.; Mourikis, A.I. High-precision, consistent EKF-based visual-inertial odometry. Int. J. Robot. Res. 2013, 32, 690–711. [Google Scholar] [CrossRef]
- Bloesch, M.; Omari, S.; Hutter, M.; Siegwart, R. Robust visual inertial odometry using a direct EKF-based approach. In Proceedings of the IEEE/RSJ international conference on intelligent robots and systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 298–304. [Google Scholar]
- Murphy, R.R.; Kravitz, J.; Stover, S.L.; Shoureshi, R. Mobile robots in mine rescue and recovery. IEEE Robot. Autom. Mag. 2009, 16, 91–103. [Google Scholar] [CrossRef]
- Ghamry, K.A.; Kamel, M.A.; Zhang, Y. Cooperative forest monitoring and fire detection using a team of UAVs-UGVs. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 1206–1211. [Google Scholar]
- Menna, M.; Gianni, M.; Ferri, F.; Pirri, F. Real-time autonomous 3D navigation for tracked vehicles in rescue environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 696–702. [Google Scholar]
- Wu, K.J.; Guo, C.X.; Georgiou, G.; Roumeliotis, S.I. Vins on wheels. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5155–5162. [Google Scholar]
- Fritsche, P.; Zeise, B.; Hemme, P.; Wagner, B. Fusion of radar, LiDAR and thermal information for hazard detection in low visibility environments. In Proceedings of the IEEE International Symposium on Safety, Security and Rescue Robotics (SSRR), Shanghai, China, 11–13 October 2017; pp. 96–101. [Google Scholar]
- Lichtsteiner, P.; Posch, C.; Delbruck, T. A 128 × 128 120 dB 15 μs Latency Asynchronous Temporal Contrast Vision Sensor. IEEE J. Solid-State Circuits 2008, 43, 566–576. [Google Scholar] [CrossRef]
- Keselman, L.; Woodfill, J.I.; Grunnet-Jepsen, A.; Bhowmik, A. Intel (r) realsense (tm) stereoscopic depth cameras. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1267–1276. [Google Scholar]
- Carfagni, M.; Furferi, R.; Governi, L.; Santarelli, C.; Servi, M.; Uccheddu, F.; Volpe, Y. Metrological and Critical Characterization of the Intel D415 Stereo Depth Camera. Sensors 2019, 19, 489. [Google Scholar] [CrossRef]
- Intel RealSense Depth Camera D435i. Available online: https://www.intelrealsense.com/depth-camera-d435i (accessed on 14 May 2019).
- Yang, K.; Wang, K.; Hu, W.; Bai, J. Expanding the detection of traversable area with RealSense for the visually impaired. Sensors 2016, 16, 1954. [Google Scholar] [CrossRef]
- Vit, A.; Shani, G. Comparing RGB-D Sensors for Close Range Outdoor Agricultural Phenotyping. Sensors 2018, 18, 4413. [Google Scholar] [CrossRef]
- Available online: https://robotics.shanghaitech.edu.cn/datasets/VINS-RGBD (accessed on 14 May 2019).
- Available online: https://github.com/STAR-Center/VINS-RGBD (accessed on 14 May 2019).
- Klein, G.; Murray, D. Parallel tracking and mapping for small AR workspaces. In Proceedings of the 2007 6th IEEE and ACM International Symposium on Mixed and Augmented Reality; IEEE Computer Society: Washington, DC, USA, 2007; pp. 1–10. [Google Scholar]
- Gálvez-López, D.; Tardos, J.D. Bags of binary words for fast place recognition in image sequences. IEEE Trans. Robot. 2012, 28, 1188–1197. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Scaramuzza, D. Performance evaluation of 1-point-RANSAC visual odometry. J. Field Robot. 2011, 28, 792–811. [Google Scholar] [CrossRef]
- Ortin, D.; Montiel, J.M.M. Indoor robot motion based on monocular images. Robotica 2001, 19, 331–342. [Google Scholar] [CrossRef]
- Choi, S.; Kim, J.H. Fast and reliable minimal relative pose estimation under planar motion. Image Vis. Comput. 2018, 69, 103–112. [Google Scholar] [CrossRef]
- Weiss, S.; Achtelik, M.W.; Lynen, S.; Chli, M.; Siegwart, R. Real-time onboard visual-inertial state estimation and self-calibration of mavs in unknown environments. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 957–964. [Google Scholar]
- Lynen, S.; Achtelik, M.W.; Weiss, S.; Chli, M.; Siegwart, R. A robust and modular multi-sensor fusion approach applied to mav navigation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3923–3929. [Google Scholar]
- Mourikis, A.I.; Roumeliotis, S.I. A multi-state constraint Kalman filter for vision-aided inertial navigation. In Proceedings of the IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 3565–3572. [Google Scholar]
- Leutenegger, S.; Furgale, P.; Rabaud, V.; Chli, M.; Konolige, K.; Siegwart, R. Keyframe-based visual-inertial slam using nonlinear optimization. In Proceedings of the 2013 Robotics: Science and Systems Conference, Berlin, Germany, 24–28 June 2013. [Google Scholar]
- Qin, T.; Cao, S.; Pan, J.; Shen, S. A General Optimization-based Framework for Global Pose Estimation with Multiple Sensors. arXiv 2019, arXiv:1901.03642. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. Visual-inertial monocular SLAM with map reuse. IEEE Robot. Autom. Lett. 2017, 2, 796–803. [Google Scholar] [CrossRef]
- Mu, X.; Chen, J.; Zhou, Z.; Leng, Z.; Fan, L. Accurate Initial State Estimation in a Monocular Visual-Inertial SLAM System. Sensors 2018, 18, 506. [Google Scholar]
- Hong, E.; Lim, J. Visual-Inertial Odometry with Robust Initialization and Online Scale Estimation. Sensors 2018, 18, 4287. [Google Scholar] [CrossRef]
- Guo, C.X.; Roumeliotis, S.I. IMU-RGBD camera 3D pose estimation and extrinsic calibration: Observability analysis and consistency improvement. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 2935–2942. [Google Scholar]
- Brunetto, N.; Salti, S.; Fioraio, N.; Cavallari, T.; Stefano, L. Fusion of inertial and visual measurements for rgb-d slam on mobile devices. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Santiago, Chile, 11–12 and 17–18 December 2015; pp. 1–9. [Google Scholar]
- Falquez, J.M.; Kasper, M.; Sibley, G. Inertial aided dense & semi-dense methods for robust direct visual odometry. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, South Korea, 9–14 October 2016; pp. 3601–3607. [Google Scholar]
- Laidlow, T.; Bloesch, M.; Li, W.; Leutenegger, S. Dense RGB-D-inertial SLAM with map deformations. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6741–6748. [Google Scholar]
- Zhu, Z.; Xu, F. Real-time Indoor Scene Reconstruction with RGBD and Inertia Input. arXiv 2018, arXiv:1812.03015. [Google Scholar]
- Wang, C.; Hoang, M.C.; Xie, L.; Yuan, J. Non-iterative RGB-D-inertial Odometry. arXiv 2017, arXiv:1710.05502. [Google Scholar]
- Ling, Y.; Liu, H.; Zhu, X.; Jiang, J.; Liang, B. RGB-D Inertial Odometry for Indoor Robot via Keyframe-based Nonlinear Optimization. In Proceedings of the IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 973–979. [Google Scholar]
- Herbert, M.; Caillas, C.; Krotkov, E.; Kweon, I.S.; Kanade, T. Terrain mapping for a roving planetary explorer. In Proceedings of the International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989; pp. 997–1002. [Google Scholar]
- Triebel, R.; Pfaff, P.; Burgard, W. Multi-level surface maps for outdoor terrain mapping and loop closing. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 2276–2282. [Google Scholar]
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robots 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Yang, S.; Yang, S.; Yi, X.; Yang, W. Real-time globally consistent 3D grid mapping. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 929–935. [Google Scholar]
- Delmerico, J.; Scaramuzza, D. A benchmark comparison of monocular visual-inertial odometry algorithms for flying robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 2502–2509. [Google Scholar]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. 1981. Available online: https://ri.cmu.edu/pub_files/pub3/lucas_bruce_d_1981_2/lucas_bruce_d_1981_2.pdf (accessed on 14 May 2019).
- Shi, J.; Tomasi, C. Good Features to Track; Technical Report; Cornell University: Ithaca, NY, USA, 1993. [Google Scholar]
- Forster, C.; Carlone, L.; Dellaert, F.; Scaramuzza, D. On-Manifold Preintegration for Real-Time Visual–Inertial Odometry. IEEE Trans. Robot. 2017, 33, 1–21. [Google Scholar] [CrossRef]
- Rehder, J.; Nikolic, J.; Schneider, T.; Hinzmann, T.; Siegwart, R. Extending kalibr: Calibrating the extrinsics of multiple imus and of individual axes. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4304–4311. [Google Scholar]
- Zhi, X.; Schwertfeger, S. Simultaneous hand-eye calibration and reconstruction. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1470–1477. [Google Scholar]
- Civera, J.; Davison, A.J.; Montiel, J.M. Inverse depth parametrization for monocular SLAM. IEEE Trans. Robot. 2008, 24, 932–945. [Google Scholar] [CrossRef]
- Sibley, G.; Matthies, L.; Sukhatme, G. Sliding window filter with application to planetary landing. J. Field Robot. 2010, 27, 587–608. [Google Scholar] [CrossRef]
- Hesch, J.A.; Kottas, D.G.; Bowman, S.L.; Roumeliotis, S.I. Consistency analysis and improvement of vision-aided inertial navigation. IEEE Trans. Robot. 2014, 30, 158–176. [Google Scholar] [CrossRef]
- Wu, K.J.; Roumeliotis, S.I. Unobservable Directions of VINS under Special Motions; Department of Computer Science & Engineering, University of of Minnesota: Minneapolis, MN, USA, 2016. [Google Scholar]
- Nistér, D. An efficient solution to the five-point relative pose problem. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 756–777. [Google Scholar] [CrossRef]
- Gao, X.S.; Hou, X.R.; Tang, J.; Cheng, H.F. Complete solution classification for the perspective-three-point problem. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 930–943. [Google Scholar]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. Epnp: An accurate o (n) solution to the pnp problem. Int. J. Comput. Vis. 2009, 81, 155. [Google Scholar] [CrossRef]
- Penate-Sanchez, A.; Andrade-Cetto, J.; Moreno-Noguer, F. Exhaustive linearization for robust camera pose and focal length estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2387–2400. [Google Scholar] [CrossRef]
- Agarwal, S.; Mierle, K. Ceres Solver. 2012. Available online: http://ceres-solver.org/ (accessed on 14 May 2019).
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures; International Society for Optics and Photonics: Bellingham, WA, USA, 1992; Volume 1611, pp. 586–607. [Google Scholar]
- Meagher, D. Geometric modeling using octree encoding. Comput. Graphics Image Process. 1982, 19, 129–147. [Google Scholar] [CrossRef]
- Burri, M.; Nikolic, J.; Gohl, P.; Schneider, T.; Rehder, J.; Omari, S.; Achtelik, M.W.; Siegwart, R. The EuRoC micro aerial vehicle datasets. Int. J. Robot. Res. 2016, 35, 1157–1163. [Google Scholar] [CrossRef]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, 7–12 October 2012; pp. 573–580. [Google Scholar]
- OptiTrack. Available online: https://optitrack.com (accessed on 14 May 2019).
- Zhang, Z.; Scaramuzza, D. A tutorial on quantitative trajectory evaluation for visual (-inertial) odometry. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7244–7251. [Google Scholar]
- Jackal. Available online: https://www.clearpathrobotics.com/jackal-small-unmanned-ground-vehicle (accessed on 14 May 2019).
- ASTM 2827-11 Crossing Pitch/Roll Ramps. Available online: https://www.astm.org/Standards/E2827.htm (accessed on 14 May 2019).
- Sheh, R.; Schwertfeger, S.; Visser, A. 16 Years of RoboCup Rescue. KI-Künstliche Intelligenz 2016, 30, 267–277. [Google Scholar] [CrossRef] [Green Version]
- Sheh, R.; Jacoff, A.; Virts, A.M.; Kimura, T.; Pellenz, J.; Schwertfeger, S.; Suthakorn, J. Advancing the state of urban search and rescue robotics through the RoboCupRescue robot league competition. In Field and Service Robotics; Springer: Berlin, Germany, 2014. [Google Scholar]




















| Experiment | VINS-RGBD | VINS-RGBD with Loop | VINS-Mono | VINS-Mono with Loop |
|---|---|---|---|---|
| Handheld Simple | 0.07 | - | 0.24 | - |
| Handheld Normal | 0.13 | - | 0.20 | - |
| Handheld With more Rotation | 0.18 | 0.20 | 0.23 | 0.23 |
| Wheeled Slow | 0.20 | 0.16 | 0.39 | 0.27 |
| Wheeled Normal | 0.17 | 0.09 | 0.18 | 0.09 |
| Wheeled Fast | 0.23 | 0.20 | 0.63 | 0.31 |
| Tracked 1 Ground and Up-down Slopes | 0.11 | 0.10 | x | x |
| Tracked 2 Cross and Up-down Slopes | 0.17 | 0.23 | x | x |
| Tracked 3 Cross and Up-down Slopes and Ground | 0.21 | 0.24 | 0.77 | 0.75 |
| Scene | Octree Resolution (m) | Origin (Points) | Octree 5pts | Octree 3pts | Octree 1pt | Loop Cost 5pts (ms) | Speed up (5pts) |
|---|---|---|---|---|---|---|---|
| lab (large) | 0.05 | 3,981,242 | 2,026,884 | 1,562,519 | 760,411 | 378 | 49.1% |
| arena (middle) | 0.02 | 6,153,656 | 849,748 | 619,237 | 284,029 | 159 | 86.2% |
| arena (small) | 0.02 | 4,259,847 | 198,161 | 128,615 | 48,091 | 37 | 95.3% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, Z.; Li, R.; Schwertfeger, S. RGBD-Inertial Trajectory Estimation and Mapping for Ground Robots. Sensors 2019, 19, 2251. https://doi.org/10.3390/s19102251
Shan Z, Li R, Schwertfeger S. RGBD-Inertial Trajectory Estimation and Mapping for Ground Robots. Sensors. 2019; 19(10):2251. https://doi.org/10.3390/s19102251
Chicago/Turabian StyleShan, Zeyong, Ruijian Li, and Sören Schwertfeger. 2019. "RGBD-Inertial Trajectory Estimation and Mapping for Ground Robots" Sensors 19, no. 10: 2251. https://doi.org/10.3390/s19102251
APA StyleShan, Z., Li, R., & Schwertfeger, S. (2019). RGBD-Inertial Trajectory Estimation and Mapping for Ground Robots. Sensors, 19(10), 2251. https://doi.org/10.3390/s19102251





