Analyzing the Impact of Traffic Congestion Mitigation: From an Explainable Neural Network Learning Framework to Marginal Effect Analyses
Abstract
:1. Introduction
- The gap between layers 1 and 2 is related to the wide variety of available traffic data sources and the fact that core traffic network models are typically difficult to calibrate consistently.
- The gap between layers 2 and 3 lies in the fact that traffic models contain many elements with limited certainty, whereas mission-critical scenario evaluation requires reliable current-state estimates and policy-sensitive forecasts.
2. Literature Review
2.1. Model-Driven Travel Demand Estimation Approaches
2.2. Data-Driven Travel Demand Estimation Approaches
2.3. Existing Congestion Mitigation Strategies
2.4. Outline
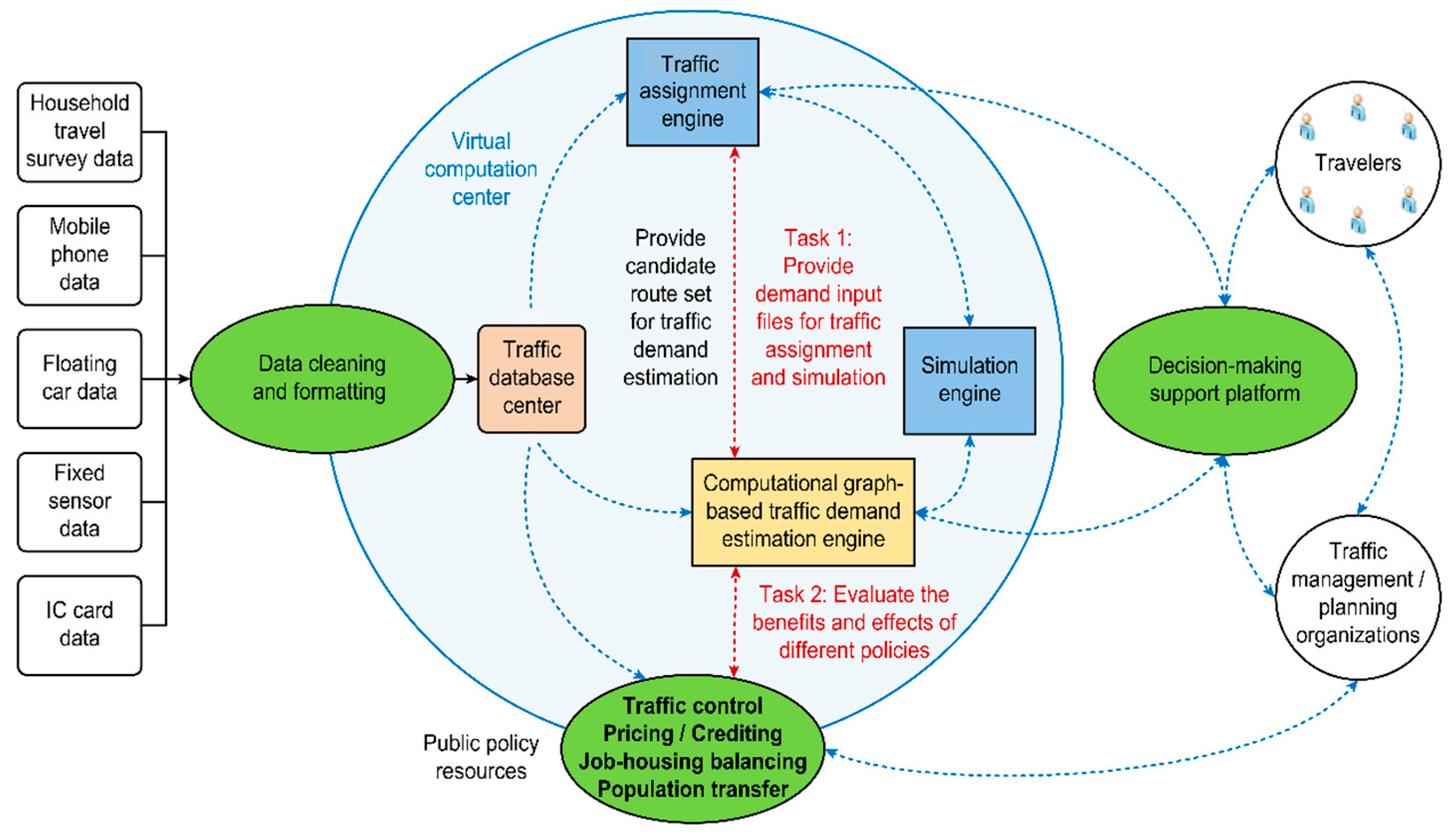
3. System Architecture and Conceptual Illustration
3.1. System Architecture
- Estimate multilayered traffic demands (i.e., trip generation, trip distribution, and path/link flows).
- Produce the input file for the traffic assignment engine.
- Evaluate the effects of various transport policies.
3.2. Computational Graphs and Marginal Effect Analyses
3.2.1. Comparison between Discrete Choice Modeling and Computational Graph Modeling Based on a Mode-Split Model
- The first layer is a stack of neurons that express the utility function of the differences between pairs of alternatives for predicting the DA probability:Consider ; then,where can be viewed as a vector that includes both income and travel time.
- The second layer applies the logistic sigmoid function, , as an activation function to squeeze the output of the linear utility function into the interval (0, 1).
- The third layer calculates the probability of choosing DA:
- can be calculated by multiplying the partial derivatives on the path ①→②→③→⑥→⑦:
- can be calculated by summing the multiplied partial derivatives on the path ①→②→③→④→⑨ with the multiplied partial derivatives on the path ①→②→③→⑤→⑧:
3.2.2. Marginal Effect Analyses Using a Computational Graph
4. Congestion Mitigation Strategies Based on the Computational-Graph-Based Learning System
4.1. Variables
- indicates the trip generation variable vector, containing the trip generation results from all zones.
- indicates the trip distribution variable vector, containing the flow volume between all OD pairs.
- indicates the path flow variable vector, containing all flow volume on each path in the candidate route set generated by the traffic assignment engine.
- indicates the link flow variable vector, containing the flow volume on each link in the network.
- indicates the OD split rate variable matrix expressing the rate at which each OD pair is selected from each traffic zone.
- indicates the route choice proportion variable matrix, expressing the rate at which each route between each OD pair is selected.
- denotes the utility of route , where
- is the toll cost of the route, which is calculated by aggregating the link toll on each related link, and
- is the observed travel time of the route, which is calculated by approximately aggregating the observed link travel time for each related link.
- indicates the variable vector collecting all between each OD pair, .
- indicates the variable vector collecting all between each OD pair, .
- indicates the variable vector collecting all between each OD pair, .
4.2. System Equations to Express the Computational Graph
4.3. Mapping of Data Measurements on the Computational Graph
4.4. Mapping of Congestion Strategies on the Layers of the Computational Graph
- 1.
- If , the policy decreases the total travel time for users and has a positive effect.
- 2.
- If , the policy increases the total travel time for users and has a negative effect.
4.5. Algorithm
- Step 1.
- Estimation:
- Step 1.1.
- The forward passing step implements trip generation, trip distribution estimation, and traffic assignment.
- Step 1.2.
- The backward propagation step updates the estimated variables using the SGD algorithm.
- Step 1.3.
- Steps 1.1. and 1.2. are iteratively implemented until convergence is reached.
- Step 2.
- Evaluation:Step 2.1. Different mitigation strategies are evaluated by calculating their MEs on link volume.
5. Numerical Examples
5.1. A Case Study Based on the Sioux Falls Network
- One sample of survey data: Reference trip generation results for 5 zones (i.e., zones 1, 2, 7, 13, and 20).
- One sample of mobile phone data: Reference OD split rates for 20 OD pairs (i.e., origin zones 1, 2, 7, 13, and 20 and destination zones 9, 11, 22, and 24).
- One sample of floating car data: We enumerated all candidate paths between the 20 OD pairs, then randomly selected 7 of these paths and adopted assumed route choice proportions for them.
- One sample of sensor data: We assigned assumed link counts to 7 links.
5.1.1. Calibration Using Multiple Data Sources
5.1.2. Analysis of Congestion Components
- 2→1→3→12→13→24.
- 1→3→12→13→24→21→22.
- 1→3→12→13→24→23→22.
5.1.3. Marginal Effect Analysis
- In Figure 9A,B, the toll successfully decreases the flows and travel times on links (3, 12) and (1, 3). It also reduces the total travel time on all links. Interestingly, although both links (3, 12) and (1, 3) are congested (465 vehicles/hour and 583 vehicles/hour, respectively), imposing a toll of one extra dollar on link (1, 3) produces more benefit than doing the same on link (3, 12). The former policy reduces the number of vehicles in the system by 44 (ME = 44 vehicles), while the latter results in a decrease of only 4 vehicles (ME = 4 vehicles). These findings demonstrate that similar pricing policies can have different effects.
- As shown in Figure 9C, if one user changes his/her destination from node 24 to node 9, then the traffic flows on links (3, 12), (12, 13), and (13, 24) will decrease (by 0.7 vehicles/hour, 0.99 vehicles/hour, and 0.99 vehicle/hour, respectively). This figure justifies the importance of job-housing balancing in urban planning.
- We also find that the impacts of the policies on the flows and travel times are complex, with some mitigation strategies potentially decreasing the overall welfare of the system. For the scenario depicted in Figure 9D, the ME corresponds to an increase of 9.89 vehicles in the system. The policy actually decreases the flow levels (by approximately 0.4 vehicles/hour) on links (3, 4), (4, 5), and (12, 11) (links 6, 9, and 36, respectively, in the plot); however, these three links are not approaching their capacities in their current states (257.3 vehicles/hour, 116 vehicles/hour, and 216 vehicles/hour, respectively; see the Appendix A). Unfortunately, the strategy also guides additional traffic flows (approximately 0.9 vehicles/hour) to links (12, 13) and (13, 24), which are already congested (391 vehicles/hour and 615 vehicles/hour, respectively). This is the reason why, in the short term, sometimes the functional relocation of a metropolitan area can sometimes lead to a worse result than before.
- Figure 9E shows that the strategy of “population transfer” achieves good performance in relieving traffic congestion. As seen in Figure 9F, if methods are implemented to make fewer people from zone 1 use private cars, this strategy will also apparently increase the overall utility of the system. In particular, these policies greatly reduce the flow on the congested link (13, 24). The reason for the beneficial effects of these policies can be identified from the congestion component pie chart shown in Figure 9: In total, 42% of the flow on link (13, 24) is generated from node 1.
5.2. Application Study in a Beijing Subnetwork
- Estimated outputs: Figure 10A shows the physical network. The other panels in this figure illustrate the outputs estimated using different layers of the CG. Figure 10B displays the estimated trip distribution. As displayed in Figure 10D, the estimated link flows per hour per lane were also obtained using the proposed learning framework.
- Congestion analysis: Figure 10C shows one of the most congested links (i.e., link 4501, from node 2119 to node 2243). The estimated link flow is 8325 vehicles/hour. Based on the CG, there are a total of 2157 paths passing through link 4501. Figure 10C displays the two paths that most strongly contribute to congestion on this link (paths 20218 and 20219). Furthermore, the flow on the link comes from 557 OD pairs and 102 traffic zones. Figure 11A,B display the top 30 OD pairs and trip-generating traffic zones that contribute the most to the flow volume on link 4501. We also labelled the OD pairs and traffic zones associated with the largest volume on the map. We find that the congestion on link 4501 is primarily caused by traffic demands for travel from the southern urban area to the northern subarea.
- ME analysis: Because link 4501 and zone 83 are near several universities and companies in Beijing, one possible congestion mitigation strategy is to move some workplaces from zone 83 to zone 117. We can calculate the ME of this policy as follows. Figure 12 shows the changes in travel times and volumes on related links. Interestingly, this strategy actually increases the total volume on the links. However, it can reduce the travel times on certain highly congested links. The ME is −37.1 vehicles, which implies that the policy can indeed mitigate congestion in the traffic system.
- Calibration: The estimation processes using different data sources are shown in Figure 13. During the experiment, we normalized the estimates and the references to lie within the range of [0, 10]. We found that the different objective functions can be simultaneously estimated during the learning process.
6. Conclusions and Future Research Plans
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Link ID | Link Name | Estimated Flow (vehicles/hour) | Length (mile) | Free Flow Speed (miles/hour) | Capacity (vehicles/hour) |
|---|---|---|---|---|---|
| 1 | (1, 2) | 0.94 | 6 | 60 | 300 |
| 2 | (1, 3) | 582.59 | 4 | 60 | 300 |
| 3 | (2, 1) | 242.51 | 6 | 60 | 300 |
| 4 | (2, 6) | 96.49 | 5 | 60 | 300 |
| 5 | (3, 1) | 0 | 4 | 60 | 300 |
| 6 | (3, 4) | 257.3 | 4 | 60 | 300 |
| 7 | (3, 12) | 465.36 | 4 | 60 | 300 |
| 8 | (4, 3) | 0 | 4 | 60 | 300 |
| 9 | (4, 5) | 115.66 | 2 | 60 | 300 |
| 10 | (4, 11) | 213.08 | 6 | 60 | 300 |
| 11 | (5, 4) | 71.45 | 2 | 60 | 300 |
| 12 | (5, 6) | 0 | 4 | 60 | 300 |
| 13 | (5, 9) | 177.53 | 5 | 60 | 300 |
| 14 | (6, 2) | 0 | 5 | 60 | 300 |
| 15 | (6, 5) | 119.96 | 4 | 60 | 300 |
| 16 | (6, 8) | 42.75 | 2 | 60 | 300 |
| 17 | (7, 8) | 244.9 | 3 | 60 | 300 |
| 18 | (7, 18) | 245.92 | 2 | 60 | 300 |
| 19 | (8, 6) | 66.22 | 2 | 60 | 300 |
| 20 | (8, 7) | 17 | 3 | 60 | 300 |
| 21 | (8, 9) | 158.5 | 10 | 60 | 300 |
| 22 | (8, 16) | 45.93 | 5 | 60 | 300 |
| 23 | (9, 5) | 13.36 | 5 | 60 | 300 |
| 24 | (9, 8) | 0 | 10 | 60 | 300 |
| 25 | (9, 10) | 27.45 | 3 | 60 | 300 |
| 26 | (10, 9) | 376.53 | 3 | 60 | 300 |
| 27 | (10, 11) | 45.45 | 5 | 60 | 300 |
| 28 | (10, 15) | 30.2 | 6 | 60 | 300 |
| 29 | (10, 16) | 0 | 5 | 60 | 300 |
| 30 | (10, 17) | 0 | 8 | 60 | 300 |
| 31 | (11, 4) | 0 | 6 | 60 | 300 |
| 32 | (11, 10) | 153.29 | 5 | 60 | 300 |
| 33 | (11, 12) | 0 | 6 | 60 | 300 |
| 34 | (11, 14) | 17.99 | 4 | 60 | 300 |
| 35 | (12, 3) | 140.07 | 4 | 60 | 300 |
| 36 | (12, 11) | 215.78 | 6 | 60 | 300 |
| 37 | (12, 13) | 390.75 | 3 | 60 | 300 |
| 38 | (13, 12) | 281.24 | 3 | 60 | 300 |
| 39 | (13, 24) | 614.86 | 4 | 60 | 300 |
| 40 | (14, 11) | 78.82 | 4 | 60 | 300 |
| 41 | (14, 15) | 0 | 5 | 60 | 300 |
| 42 | (14, 23) | 17.99 | 4 | 60 | 300 |
| 43 | (15, 10) | 117.69 | 6 | 60 | 300 |
| 44 | (15, 14) | 6.83 | 5 | 60 | 300 |
| 45 | (15, 19) | 0 | 4 | 60 | 300 |
| 46 | (15, 22) | 30.2 | 4 | 60 | 300 |
| 47 | (16, 8) | 0 | 5 | 60 | 300 |
| 48 | (16, 10) | 153.75 | 5 | 60 | 300 |
| 49 | (16, 17) | 0 | 2 | 60 | 300 |
| 50 | (16, 18) | 17.86 | 3 | 60 | 300 |
| 51 | (17, 10) | 0 | 8 | 60 | 300 |
| 52 | (17, 16) | 0 | 2 | 60 | 300 |
| 53 | (17, 19) | 0 | 2 | 60 | 300 |
| 54 | (18, 7) | 78.78 | 2 | 60 | 300 |
| 55 | (18, 16) | 125.67 | 3 | 60 | 300 |
| 56 | (18, 20) | 204.05 | 4 | 60 | 300 |
| 57 | (19, 15) | 58.78 | 4 | 60 | 300 |
| 58 | (19, 17) | 0 | 2 | 60 | 300 |
| 59 | (19, 20) | 0 | 4 | 60 | 300 |
| 60 | (20, 18) | 144.72 | 4 | 60 | 300 |
| 61 | (20, 19) | 58.78 | 4 | 60 | 300 |
| 62 | (20, 21) | 306.22 | 6 | 60 | 300 |
| 63 | (20, 22) | 333.84 | 5 | 60 | 300 |
| 64 | (21, 20) | 0 | 6 | 60 | 300 |
| 65 | (21, 22) | 292.64 | 2 | 60 | 300 |
| 66 | (21, 24) | 132.01 | 3 | 60 | 300 |
| 67 | (22, 15) | 65.74 | 4 | 60 | 300 |
| 68 | (22, 20) | 0 | 5 | 60 | 300 |
| 69 | (22, 21) | 0 | 2 | 60 | 300 |
| 70 | (22, 23) | 59.1 | 4 | 60 | 300 |
| 71 | (23, 14) | 71.99 | 4 | 60 | 300 |
| 72 | (23, 22) | 118.18 | 4 | 60 | 300 |
| 73 | (23, 24) | 77.09 | 2 | 60 | 300 |
| 74 | (24, 13) | 0 | 4 | 60 | 300 |
| 75 | (24, 21) | 118.42 | 3 | 60 | 300 |
| 76 | (24, 23) | 190.17 | 2 | 60 | 300 |
References
- Lomax, T.J.; Schrank, D.L. The 2002 Urban Mobility Report; Texas Transportation Institute, Texas A&M University: College Station, TX, USA, 2002. [Google Scholar]
- Toole, J.L.; Colak, S.; Sturt, B.; Alexander, L.P.; Evsukoff, A.; González, M.C. The path most traveled: travel demand estimation using big data resources. Transp. Res. Part C Emerg. Technol. 2015, 58, 162–177. [Google Scholar] [CrossRef]
- Zhou, X.; Qin, X.; Mahmassani, H.S. Dynamic origin-destination demand estimation with multiday link traffic counts for planning applications. Transp. Res. Record 2003, 1831, 30–38. [Google Scholar] [CrossRef]
- Zhou, X.; Mahmassani, H.S. Dynamic origin-destination demand estimation using automatic vehicle identification data. IEEE Trans. Intell. Transp. Syst. 2006, 7, 105–114. [Google Scholar] [CrossRef]
- Zhou, X.; Mahmassani, H.S. A structural state space model for real-time traffic origin–destination demand estimation and prediction in a day-to-day learning framework. Transp. Res. Part B Methodol. 2007, 41, 823–840. [Google Scholar] [CrossRef]
- Lu, C.-C.; Zhou, X.; Zhang, K. Dynamic origin–destination demand flow estimation under congested traffic conditions. Transp. Res. Part C Emerg. Technol. 2013, 34, 16–37. [Google Scholar] [CrossRef]
- Asakura, Y.; Hato, E. Tracking survey for individual travel behaviour using mobile communication instruments. Transp. Res. Part C Emerg. Technol. 2004, 12, 273–291. [Google Scholar] [CrossRef]
- Zhao, Y.; Kockelman, K.M. The propagation of uncertainty through travel demand models: an exploratory analysis. Ann. Reg. Sci. 2002, 36, 145–163. [Google Scholar] [CrossRef]
- Han, K.; Yao, T.; Friesz, T.L. Lagrangian-based Hydrodynamic Model: Freeway Traffic Estimation. arXiv 2012, arXiv:1211.4619. [Google Scholar]
- Kachroo, P.; Sastry, S. Traffic assignment using a density-based travel-time function for intelligent transportation systems. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1438–1447. [Google Scholar] [CrossRef]
- Alvarez, P.; Hadi, M.; Zhan, C. Data archives of intelligent transportation systems used to support traffic simulation. Transp. Res. Record 2010, 2161, 29–39. [Google Scholar] [CrossRef]
- Kim, K.-O.; Rilett, L.R. Simplex-based calibration of traffic microsimulation models with intelligent transportation systems data. Transp. Res. Record 2003, 1855, 80–89. [Google Scholar] [CrossRef]
- Caceres, N.; Wideberg, J.P.; Benitez, F.G. Deriving origin destination data from a mobile phone network. IET Intell. Transp. Syst. 2007, 1, 15–26. [Google Scholar] [CrossRef]
- Calabrese, F.; Diao, M.; Di Lorenzo, G.; Ferreira, J.; Ratti, C. Understanding individual mobility patterns from urban sensing data: A mobile phone trace example. Transp. Res. Part C Emerg. Technol. 2013, 26, 301–313. [Google Scholar] [CrossRef]
- Available online: http://usblogs.pwc.com/emerging-technology/top-10-ai-tech-trends-for-2018/ (accessed on 5 December 2017).
- Seo, T.; Bayen, A.M.; Kusakabe, T.; Asakura, Y. Traffic state estimation on highway: A comprehensive survey. Annu. Rev. Control 2017, 43, 128–151. [Google Scholar] [CrossRef]
- Van Zuylen, H.J.; Willumsen, L.G. The most likely trip matrix estimated from traffic counts. Transp. Res. Part B Methodol. 1980, 14, 281–293. [Google Scholar] [CrossRef]
- Small, K.A.; Verhoef, E.T.; Lindsey, R. The Economics of Urban Transportation; Routledge: Abingdon, UK, 2007. [Google Scholar]
- Sheffi, Y. Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Methods; Prentice-Hall: Upper Saddle River, NJ, USA, 1985. [Google Scholar]
- Koppelman, F.S.; Bhat, C. A Self-Instructing Course in Mode Choice Modeling: Multinomial and Nested Logit Models; U.S. Department of Transportation, Federal Transit Administration: Washington, DC, USA, 2006.
- Hao, P.; Boriboonsomsin, K.; Wu, G.; Barth, M.J. Modal activity-based stochastic model for estimating vehicle trajectories from sparse mobile sensor data. IEEE Trans. Intell. Transp. Syst. 2017, 18, 701–711. [Google Scholar] [CrossRef]
- Nguyen, S. Estimating an OD Matrix from Network Data: A Network Equilibrium Approach; Publication No. 87; Universite de Montreal: Montreal, QC, Canada, 1977. [Google Scholar]
- Willumsen, L.G. Estimation of an O-D Matrix from Traffic Counts—A Review. Working Paper; University of Leeds: Leeds, UK, 1978. [Google Scholar]
- Tavana, H. Internally-Consistent Estimation of Dynamic Network Origin-Destination Flows from Intelligent Transportation Systems Data Using Bi-Level Optimization; The University of Texas: Austin, TX, USA, 2001. [Google Scholar]
- Ben-Akiva, M.; Bierlaire, M.; Koutsopoulos, H.; Mishalani, R. DynaMIT: A Simulation-Based System for Traffic Prediction. In DACCORD Short Term Forecasting Workshop; Massachusetts Institute of Technology: Delft, The Netherlands, 1998. [Google Scholar]
- Jayakrishnan, R.; Mahmassani, H.S.; Hu, T.Y. An evaluation tool for advanced traffic information and management systems in urban networks. Transp. Res. C 1994, 2C, 129–147. [Google Scholar] [CrossRef]
- Ziliaskopoulos, A.K.; Waller, S.T. An Internet-based geographic information system that integrates data, models and users for transportation applications. Transp. Res. Part C Emerg. Technol. 2000, 8, 427–444. [Google Scholar] [CrossRef]
- Patriksson, M. The Traffic Assignment Problem: Models and Methods; Dover Publications: Mineola, NY, USA, 2015. [Google Scholar]
- Shi, Q.; Abdel-Aty, M. Big data applications in real-time traffic operation and safety monitoring and improvement on urban expressways. Transp. Res. Part C Emerg. Technol. 2015, 58, 380–394. [Google Scholar] [CrossRef]
- Mudigonda, S.; Ozbay, K. Using Big Data and Efficient Methods to Capture Stochasticity for Calibration of Macroscopic Traffic Simulation Models. In Celebrating 50 Years of Traffic Flow Theory; Transportation Research Board: Portland, OR, USA, 2014; pp. 215–232. [Google Scholar]
- Antoniou, C.; Barceló, J.; Breen, M.; Bullejos, M.; Casas, J.; Cipriani, E.; Ciuffo, B.; Djukic, T.; Hoogendoorn, S.; Marzano, V.; et al. Towards a generic benchmarking platform for origin–destination flows estimation/updating algorithms: design, demonstration and validation. Transp. Res. Part C Emerg. Technol. 2016, 66, 79–98. [Google Scholar] [CrossRef]
- Ge, Q.; Fukuda, D. Updating origin–destination matrices with aggregated data of GPS traces. Transp. Res. Part C Emerg. Technol. 2016, 69, 291–312. [Google Scholar] [CrossRef]
- Carrese, S.; Cipriani, E.; Mannini, L.; Nigro, M. Dynamic demand estimation and prediction for traffic urban networks adopting new data sources. Transp. Res. Part C Emerg. Technol. 2017, 81, 83–98. [Google Scholar] [CrossRef]
- Hu, X.; Chiu, Y.; Villalobos, J.A.; Nava, E. A sequential decomposition framework and method for calibrating dynamic origin—destination demand in a congested network. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2790–2797. [Google Scholar] [CrossRef]
- Yang, Y.; Fan, Y.; Wets, R.J.B. Stochastic travel demand estimation: improving network identifiability using multi-day observation sets. Transp. Res. Part B Methodol. 2018, 107, 192–211. [Google Scholar] [CrossRef]
- Yang, H.; Yang, C.; Gan, L. Models and algorithms for the screen line-based traffic-counting location problems. Comput. Oper. Res. 2006, 33, 836–858. [Google Scholar] [CrossRef]
- Qiu, T.Z.; Lu, X.Y.; Chow, A.H.F.; Shladover, S.E. Estimation of freeway traffic density with loop detector and probe vehicle data. Transp. Res. Record 2010, 2178, 21–29. [Google Scholar] [CrossRef]
- Dafermos, S.; Nagurney, A. On some traffic equilibrium theory paradoxes. Transp. Res. Part B Methodol. 1984, 18, 101–110. [Google Scholar] [CrossRef]
- Frederix, R.; Viti, F.; Corthout, R.; Tampère, C. New gradient approximation method for dynamic origin-destination matrix estimation on congested networks. Transp. Res. Rec. 2011, 1, 19–25. [Google Scholar] [CrossRef]
- Nigro, M.; Cipriani, E.; Giudice, A.D. Exploiting floating car data for time-dependent origin–destination matrices estimation. Intell. Transport. Syst. 2018, 22, 157–174. [Google Scholar] [CrossRef]
- Savrasovs, M.; Pticina, I. Methodology of OD Matrix Estimation Based on Video Recordings and Traffic Counts. Procedia Eng. 2017, 178, 289–297. [Google Scholar] [CrossRef]
- Bonnel, P.; Hombourger, E.; Olteanu-Raimond, A.-M.; Smoreda, Z. Passive mobile phone dataset to construct origin-destination matrix: Potentials and limitations. Transp. Res. Proced. 2015, 11, 381–398. [Google Scholar] [CrossRef]
- Yang, F.; Jin, P.J.; Cebelak, M.K.; Ran, B.; Walton, C.M. The application of venue-side location-based social networking (VS-LBSN) data in dynamic origin-destination estimation. High Comm. Refug. 2014, 4, 167–241. [Google Scholar] [CrossRef]
- Wang, F.Y. Scanning the issue and beyond: real-time social transportation with online social signals. IEEE Trans. Intell. Transp. Syst. 2014, 15, 909–914. [Google Scholar] [CrossRef]
- Jin, P.J.; Cebelak, M.K.; Yang, F.; Zhang, J.; Walton, C.M.; Ran, B. Location-based social networking data exploration into use of doubly constrained gravity model for origin-destination estimation. Transp. Res. Rec. 2014, 2430, 72–82. [Google Scholar] [CrossRef]
- Wu, X.; Guo, J.; Xian, K.; Zhou, X. Hierarchical travel demand estimation using multiple data sources: A forward and backward propagation algorithmic framework on a layered computational graph. Transp. Res. Part C Emerg. Technol. 2018, 96, 321–346. [Google Scholar] [CrossRef]
- Ma, W.; Pi, X.; Qian, S. Estimating multi-class dynamic origin-destination demand through a forward-backward algorithm on computational graphs. arXiv 2019, arXiv:1903.04681. [Google Scholar]
- Vickrey, W.S. Congestion theory and transport investment. Am. Econ. Rev. 1969, 59, 251–260. [Google Scholar]
- Amirgholy, M.; Gao, H.O. Modeling the dynamics of congestion in large urban networks using the macroscopic fundamental diagram: User equilibrium, system optimum, and pricing strategies. Transp. Res. Pt. B Methodol. 2017, 104, 215–237. [Google Scholar] [CrossRef]
- Zhu, S.J.; Du, L.Y.; Zhang, L. Rationing and pricing strategies for congestion mitigation: behavioral theory, econometric model, and application in Beijing. Transp. Res. Pt. B Methodol. 2013, 57, 210–224. [Google Scholar] [CrossRef]
- Yang, H.; Tang, Y.L. Managing rail transit peak-hour congestion with a fare-reward scheme. Transp. Res. Pt. B Methodol. 2018, 110, 122–136. [Google Scholar] [CrossRef]
- Zang, G.; Xu, M.; Gao, Z. High-occupancy vehicle lanes and tradable credits scheme for traffic congestion management: A bilevel programming approach. Promet 2018, 30, 1–10. [Google Scholar] [CrossRef]
- Mizera, C. Congestion Mitigation: Programs and Strategies. In Proceedings of the 2007 Transportation Scholars Conference, Ames, IA, USA, 9 November 2007. [Google Scholar]
- Tian, L.-J.; Yang, H.; Huang, H.-J. Tradable credit schemes for managing bottleneck congestion and modal split with heterogeneous users. Transp. Res. Part E Logist. Transp. Rev. 2013, 54, 1–13. [Google Scholar] [CrossRef]
- Zhu, D.S.; Yang, H.; Li, C.M.; Wang, X.L. Properties of the multiclass traffic network equilibria under a tradable credit scheme. Transp. Sci. 2015, 49, 519–534. [Google Scholar] [CrossRef]
- Daganzo, C.F.; Lehe, L.J. Distance-dependent congestion pricing for downtown zones. Transp. Res. Pt. B Methodol. 2015, 75, 89–99. [Google Scholar] [CrossRef]
- Liu, Y.; Nie, Y. A credit-based congestion management scheme in general two-mode networks with multiclass users. Netw. Spat. Econ. 2017, 17, 681–711. [Google Scholar] [CrossRef]
- Ramos, R.; Cantillo, V.; Arellana, J.; Sarmiento, I. From restricting the use of cars by license plate numbers to congestion charging: analysis for Medellin, Colombia. Transp. Policy 2017, 60, 119–130. [Google Scholar] [CrossRef]
- Aboudina, A.; Abdelgawad, H.; Abdulhai, B.; Habib, K.N. Time-dependent congestion pricing system for large networks: integrating departure time choice, dynamic traffic assignment and regional travel surveys in the Greater Toronto Area. Transp. Res. Part A Policy Pract. 2016, 94, 411–430. [Google Scholar] [CrossRef]
- Morton, C.; Lovelace, R.; Anable, J. Exploring the effect of local transport policies on the adoption of low emission vehicles: Evidence from the London congestion charge and hybrid electric vehicles. Transp. Policy 2017, 60, 34–46. [Google Scholar] [CrossRef]
- Wu, D.; Yin, Y.; Lawphongpanich, S. Pareto-improving congestion pricing on multimodal transportation networks. Eur. J. Op. Res. 2011, 210, 660–669. [Google Scholar] [CrossRef]
- Silva, J.; Morency, C.; Goulias, K.G. Using structural equations modeling to unravel the influence of land use patterns on travel behavior of workers in Montreal. Transp. Res. Part A Policy Pract. 2012, 46, 1252–1264. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Y.; Schweitzer, L. Jobs/housing balance and employer-based travel demand management program returns to scale: Evidence from Los Angeles. Transp. Policy 2012, 20, 22–35. [Google Scholar] [CrossRef]
- Zhou, J. From better understandings to proactive actions: Housing location and commuting mode choices among university students. Transp. Policy 2014, 33, 166–175. [Google Scholar] [CrossRef]
- Peng, Z.-R. The jobs-housing balance and urban commuting. Urban Stud. 1997, 34, 1215–1235. [Google Scholar] [CrossRef]
- Zhao, P.; Lü, B.; Roo, G.D. Impact of the jobs-housing balance on urban commuting in Beijing in the transformation era. J. Transp. Geogr. 2011, 19, 59–69. [Google Scholar] [CrossRef]
- Zhou, X.; Tong, L.; Mahmoudi, M.; Zhuge, L.; Yao, Y.; Zhang, Y.; Shi, T. Open-source VRPLite package for vehicle routing with pickup and delivery: A path finding engine for scheduled transportation systems. Urban Rail Transit 2018, 4, 68–85. [Google Scholar] [CrossRef]
- Zhuge, L.; Li, W.; Guo, J.; Xian, K.; Wu, X.; Zhou, X. A Tree-Based Reoptimization Framework for Solving Traffic Assignment Problem in Rapid Decision Making Applications. In Proceedings of the 18th COTA International Conference of Transportation Professionals: Intelligence, Connectivity, and Mobility, CICTP 2018, Beijing, China, 5–8 July 2018; pp. 205–214. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, UK, 2016. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Park, J.; Shim, K.; Lee, S.; Kim, M. Classification of Application Traffic Using Tensorflow Machine Learning. In Proceedings of the 2017 19th Asia-Pacific Network Operations and Management Symposium (APNOMS), Seoul, Korea, 27–29 September 2017; pp. 391–394. [Google Scholar]
- Bergstra, J.; Bastien, F.; Breuleux, O. Theano: Deep Learning on GPUs with Python. In Big Learn Workshop, NIPS’11; Microtome Publishing: Granada, Spain, 2011; pp. 1–48. [Google Scholar]
- GitHub. Calculus on Computational Graphs: Backpropagation. Available online: http://colah.github.io/posts/2015-08-Backprop/ (accessed on 31 August 2015).
- Zhao, X.; Yan, X.; Yu, A.; Van Hentenryck, P. Modeling stated preference for mobility-on-demand transit: A comparison of machine learning and logit models. arXiv 2018, arXiv:1811.01315. [Google Scholar]
- Hensher, D.A.; Button, K. Handbook of Transport Modelling; Emerald Group Publishing Limited: Bingley, UK, 2007. [Google Scholar]
- Chen, C.; Ma, J.; Susilo, Y.; Liu, Y.; Wang, M. The promises of big data and small data for travel behavior (aka human mobility) analysis. Transp. Res. Part C Emerg. Technol. 2016, 68, 285–299. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Song, Y.; Miller, H.J.; Zhou, X. Estimating the most likely space–time paths, dwell times and path uncertainties from vehicle trajectory data: A time geographic method. Transp. Res. Part C Emerg. Technol. 2016, 66, 176–194. [Google Scholar] [CrossRef]
- Lu, Z.; Rao, W.; Wu, Y.-J.; Guo, L.; Xia, J. A Kalman filter approach to dynamic OD flow estimation for urban road networks using multi-sensor data. J. Adv. Transp. 2015, 49, 210–227. [Google Scholar] [CrossRef]
- Van Lint, H.; Djukic, T. Applications of Kalman filtering in traffic management and control. In New Directions in Informatics, Optimization, Logistics, and Production; Institute for Operations Research and the Management Sciences (INFORM): Catonsville, MD, USA, 2002; pp. 59–91. [Google Scholar]
- Bertsekas, D.P. Dynamic Programming and Optimal Control; Athena Scientific: Belmont, MA, USA, 2000. [Google Scholar]
- Available online: https://github.com/Grieverwzn/Big-data-driven-computational-graph (accessed on 23 March 2019).
- Kitamura, R.; Chen, C.; Pendyala, R.M.; Narayanan, R. Micro-simulation of daily activity-travel patterns for travel demand forecasting. Transportation 2000, 27, 25–51. [Google Scholar] [CrossRef]
- Pendyala, R.M.; Kitamura, R.; Kikuchi, A.; Yamamoto, T.; Fujii, S. Florida activity mobility simulator: Overview and preliminary validation results. Transp. Res. Rec. 2005, 1921, 123–130. [Google Scholar] [CrossRef]
- Liu, J.; Kang, J.E.; Zhou, X.; Pendyala, R. Network-oriented household activity pattern problem for system optimization. Transp. Res. Procedia 2017, 23, 827–847. [Google Scholar] [CrossRef]












| Alternative | Utility | Exponent | Probability | |
|---|---|---|---|---|
| Expression | Value | |||
| Drive alone | −0.4 | 0.6703 | ||
| Transit | −1 | 0.3679 | ||
| ; | ||||
| Policy | Layer in the CG | Purpose | Variable | |
|---|---|---|---|---|
| Population transfer/ taxation | Trip generation layer | Reduce the number of users in a zone Reduce users’ trip rates | ||
| Urban functional re-layout | Trip distribution layer | Jobs-housing balance Reduce users’ travel distances | ||
| Relocation of workplaces | Trip distribution layer | Jobs-housing balance Reduce users’ travel distances | ||
| Traveler information provision | Path flow layer | Change users’ route choice behaviors | ||
| Link-/path-based pricing/credit | Path/link flow layer | Change users’ route choice behaviors | ||
| Infrastructure improvement | Path/link flow layer | Change users’ route choice behaviors |
| Model | Computational Graph (CG) | Kalman Filter (KF) |
|---|---|---|
| State variables | Trip generation Trip distribution Path/link flows | Traffic state variables OD volume |
| Traffic observations | Multiple data sources | Time-varying observations |
| Algorithm process | Recursive forward/backward propagation | Recursive prediction and updating |
| Update method | Gradient | Kalman optimal gain |
| Noise | Stochastic gradient descent | Gaussian distribution |
| Control inputs | Policies imposed offline | External influences imposed online |
| Correlation between variables | Composite function | Covariance matrix |
| State transitions | Layer-based nonlinear transitions | Stage-based linear transitions |
| From Zone | To Zone | Path Index | Node Sequence | Contributed Path Flow | Contributed OD Volume | Contributed Zone Production |
|---|---|---|---|---|---|---|
| 1 | 9 | 2 | 1→3→12→11→10→9 | 13.4 | 13.4 | 282.9 |
| 1 | 11 | 2 | 1→3→12→11 | 9.1 | 9.1 | |
| 1 | 22 | 1 | 1→3→12→13→24→21→22 | 102 | 203.7 | |
| 1 | 22 | 4 | 1→3→12→13→24→23→22 | 101.8 | ||
| 1 | 24 | 2 | 1→3→12→13→24 | 56.7 | 56.7 | |
| 2 | 9 | 3 | 2→1→3→12→11→10→9 | 7.8 | 7.8 | 182.5 |
| 2 | 11 | 3 | 2→1→3→12→11 | 44.4 | 44.4 | |
| 2 | 22 | 2 | 2→1→3→12→13→24→23→22 | 4.2 | 8.4 | |
| 2 | 22 | 3 | 2→1→3→12→13→24→21→22 | 4.2 | ||
| 2 | 24 | 2 | 2→1→3→12→13→24 | 122 | 122 | |
| Link volume | 465.4 | |||||
| From Zone | To Zone | Path Index | Node Sequence | Contributed Path Flow | Contributed OD Volume | Contributed Zone Production |
|---|---|---|---|---|---|---|
| 1 | 22 | 1 | 1→3→12→13→24→21→22 | 102 | 203.7 | 260.4 |
| 1 | 22 | 4 | 1→3→12→13→24→23→22 | 101.8 | ||
| 1 | 24 | 2 | 1→3→12→13→24 | 56.7 | 56.7 | |
| 2 | 22 | 2 | 2→1→3→12→13→24→23→22 | 4.2 | 8.4 | 130.3 |
| 2 | 22 | 3 | 2→1→3→12→13→24→21→22 | 4.2 | ||
| 2 | 24 | 2 | 2→1→3→12→13→24 | 122 | 122 | |
| 13 | 22 | 1 | 13→24→21→22 | 12.3 | 24.5 | 224.1 |
| 13 | 22 | 2 | 13→24→23→22 | 12.3 | ||
| 13 | 24 | 3 | 13→214 | 199.6 | 198.6 | |
| Link volume | 612.1 | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Guo, J.; Wu, X.; Zhu, Q.; Wu, D.; Xian, K.; Zhou, X. Analyzing the Impact of Traffic Congestion Mitigation: From an Explainable Neural Network Learning Framework to Marginal Effect Analyses. Sensors 2019, 19, 2254. https://doi.org/10.3390/s19102254
Sun J, Guo J, Wu X, Zhu Q, Wu D, Xian K, Zhou X. Analyzing the Impact of Traffic Congestion Mitigation: From an Explainable Neural Network Learning Framework to Marginal Effect Analyses. Sensors. 2019; 19(10):2254. https://doi.org/10.3390/s19102254
Chicago/Turabian StyleSun, Jianping, Jifu Guo, Xin Wu, Qian Zhu, Danting Wu, Kai Xian, and Xuesong Zhou. 2019. "Analyzing the Impact of Traffic Congestion Mitigation: From an Explainable Neural Network Learning Framework to Marginal Effect Analyses" Sensors 19, no. 10: 2254. https://doi.org/10.3390/s19102254
APA StyleSun, J., Guo, J., Wu, X., Zhu, Q., Wu, D., Xian, K., & Zhou, X. (2019). Analyzing the Impact of Traffic Congestion Mitigation: From an Explainable Neural Network Learning Framework to Marginal Effect Analyses. Sensors, 19(10), 2254. https://doi.org/10.3390/s19102254




