Magnetoimpedance Effect in the Ribbon-Based Patterned Soft Ferromagnetic Meander-Shaped Elements for Sensor Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Fabrication of Ribbon-Based Patterned Soft Ferromagnetic Multi-Turn Sensitive Elements
2.2. Measurement of Surface Magnetic Properties of the Samples
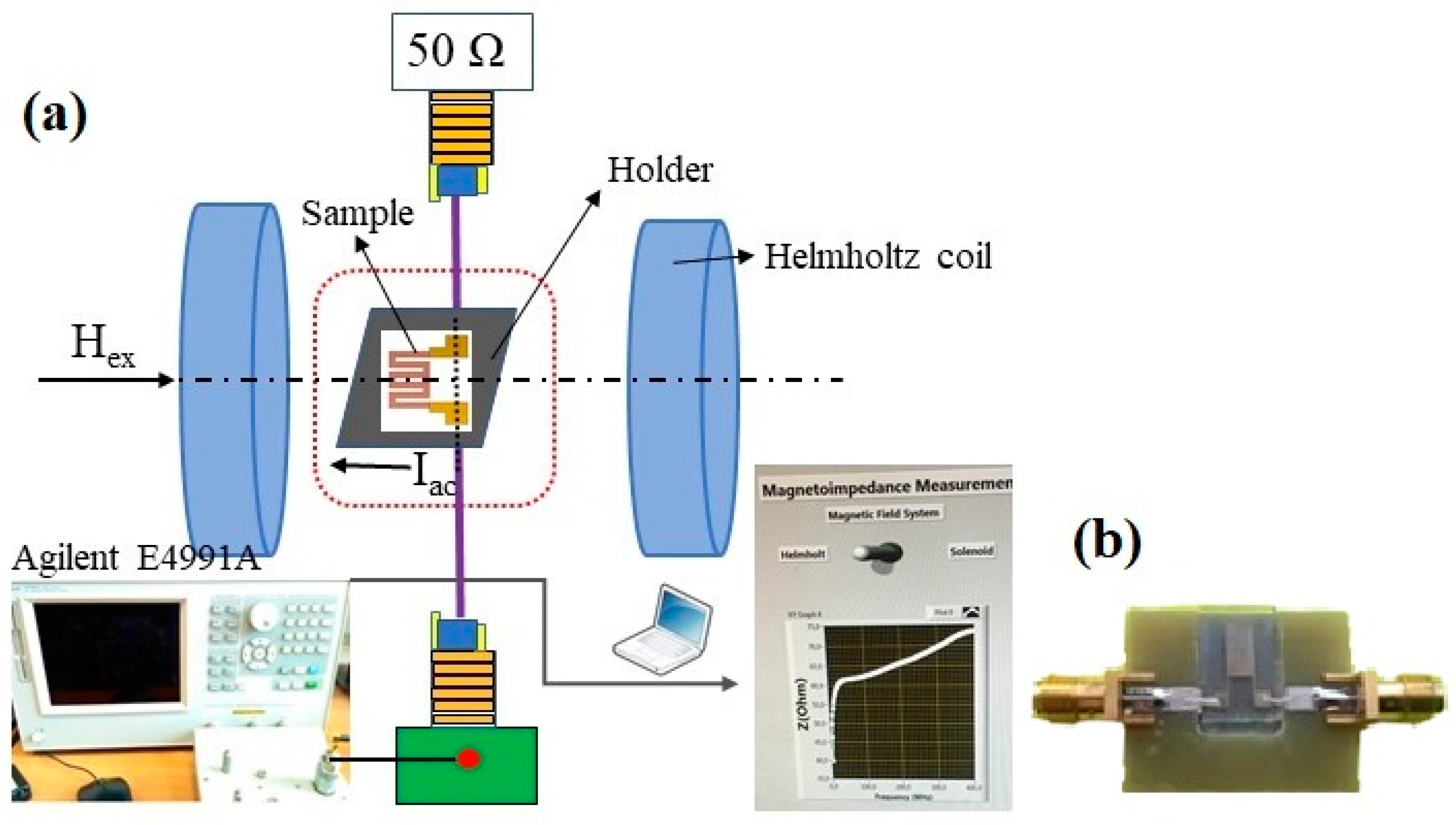
2.3. Measurement of MI
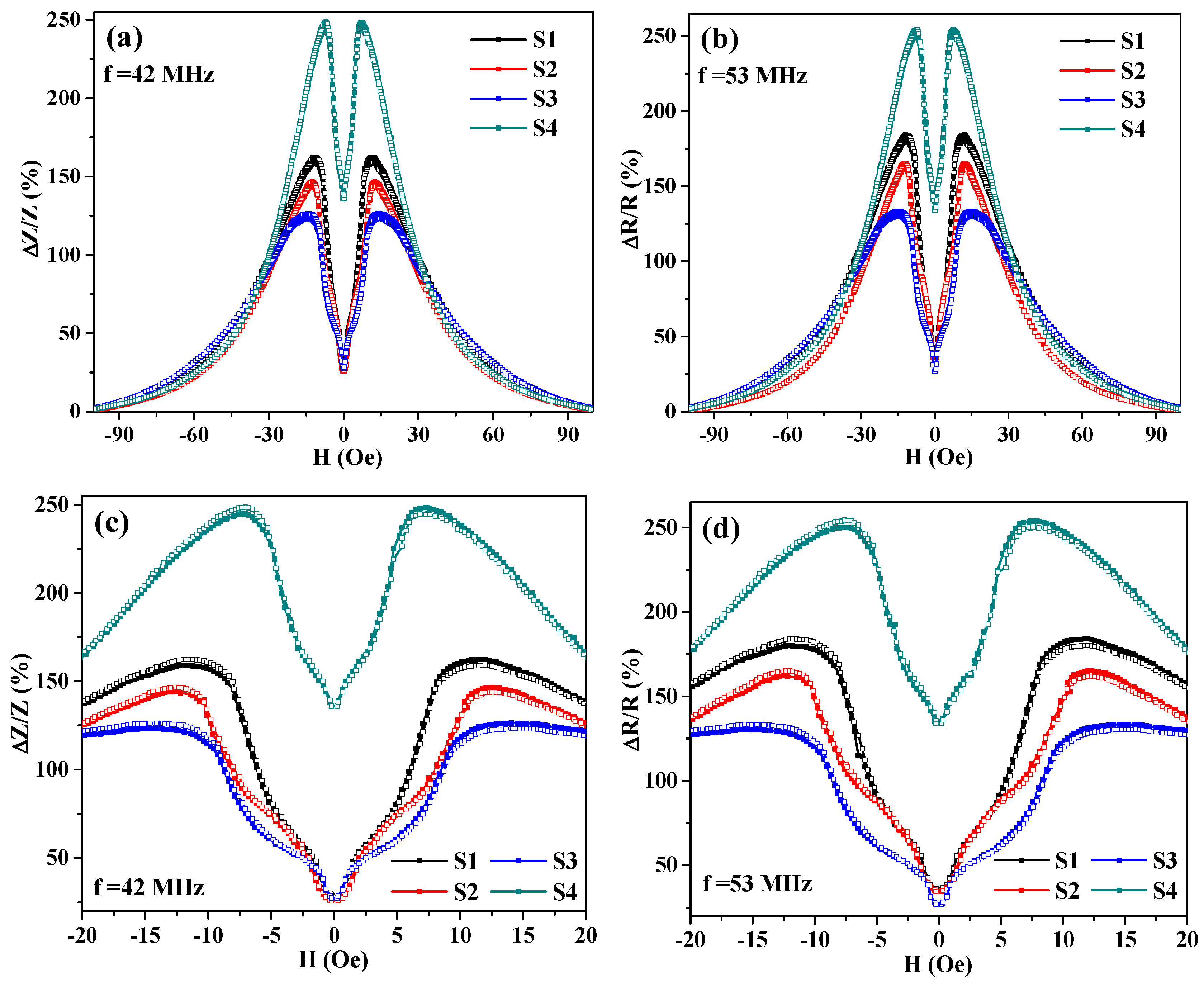
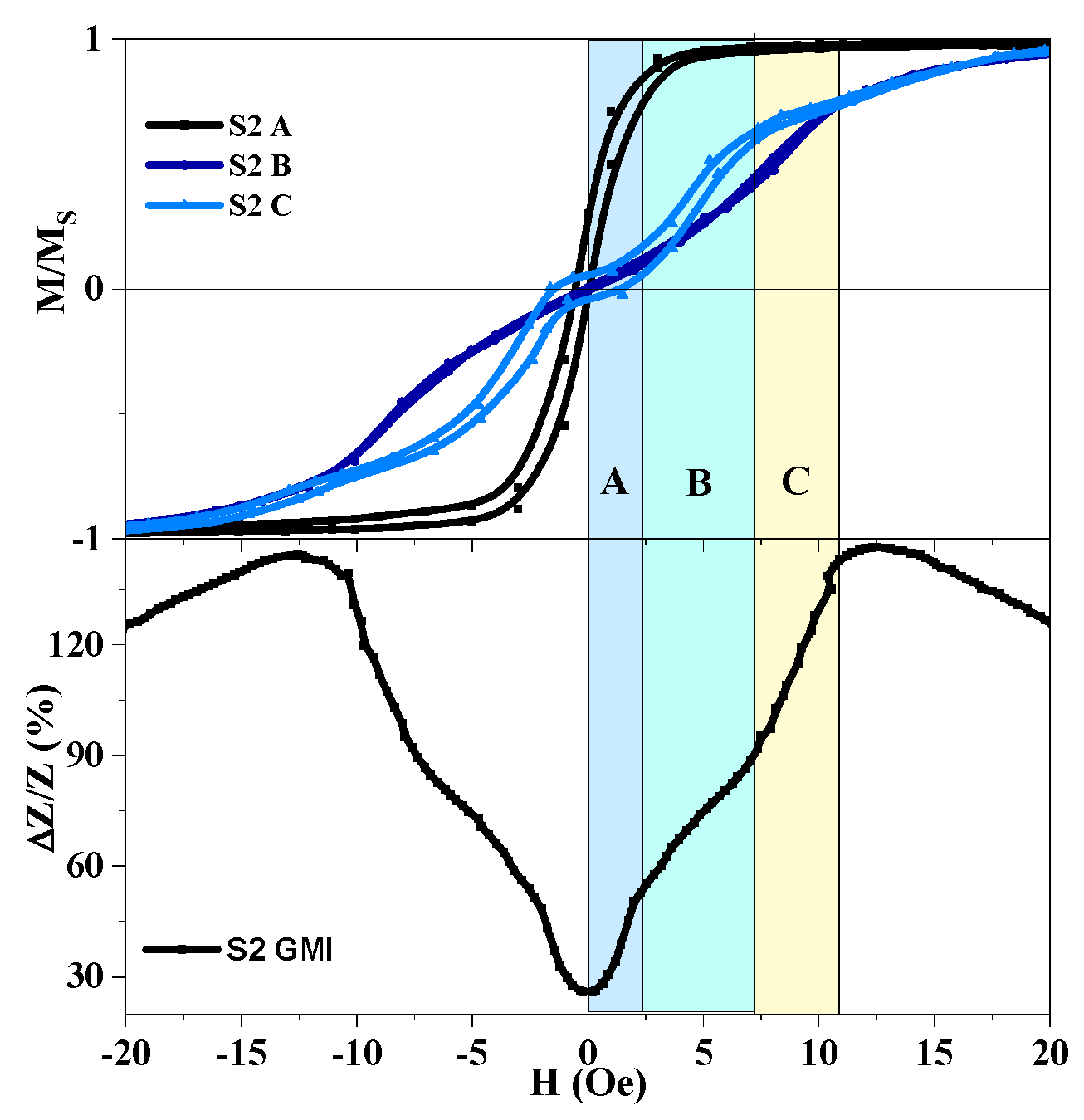
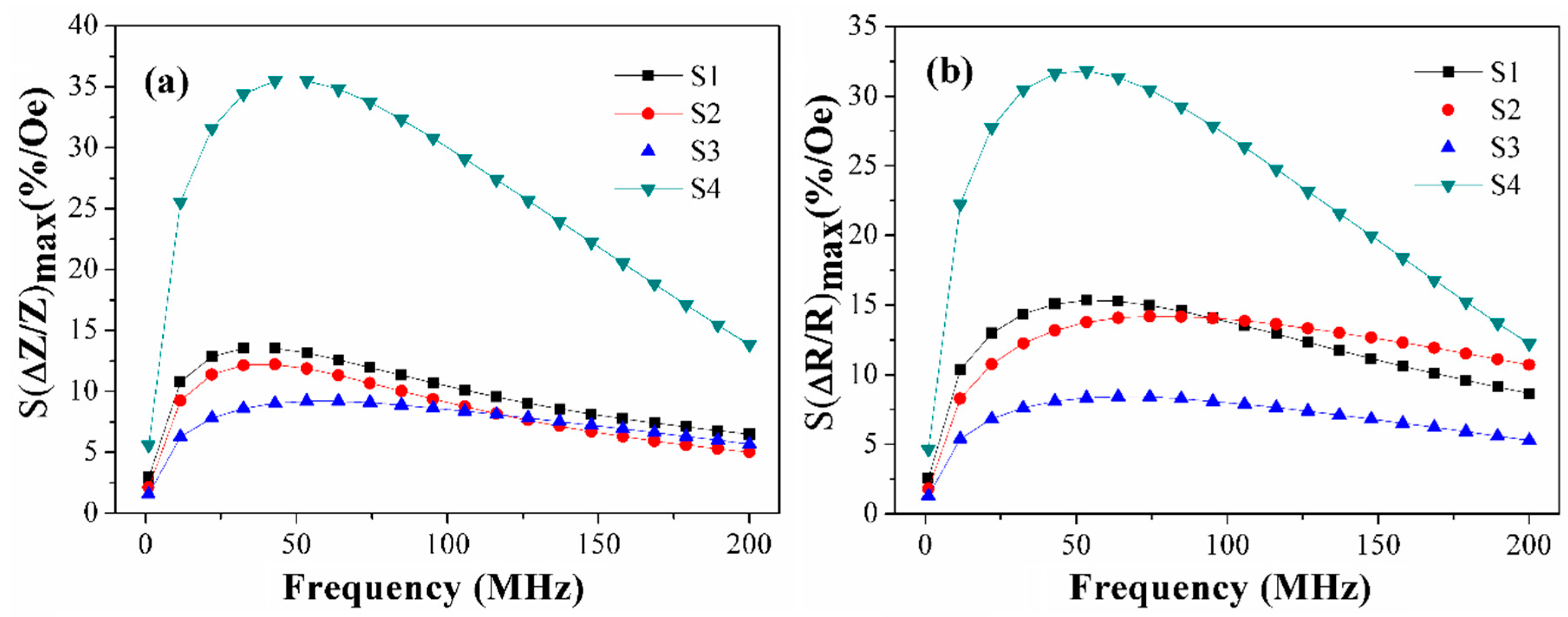
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Landau, L.D.; Lifshitz, E.M. Course of theoretical physics. In Electrodynamics of Continuous Media; Elsevier Science: Amsterdam, The Netherlands, 2013; Volume 8. [Google Scholar]
- Beach, R.; Berkowitz, A. Sensitive field-and frequency-dependent impedance spectra of amorphous FeCoSiB wire and ribbon. J. Appl. Phys. 1994, 76, 6209–6213. [Google Scholar] [CrossRef]
- Panina, L.V.; Mohri, K.; Bushida, K.; Noda, M. Giant magneto-impedance and magneto-inductive effects in amorphous alloys. J. Appl. Phys. 1994, 76, 6198–6203. [Google Scholar] [CrossRef]
- Makhotkin, V.E.; Shurukhin, B.P.; Lopatin, V.A.; Marchukov, P. Yu.; Levin, Yu. K. Magnetic field sensors based on amorphous ribbons. Sens. Actuators A 1991, 21, 759–762. [Google Scholar] [CrossRef]
- Mohri, K.; Uchiyama, T.; Panina, L.V. Recent advances of micro magnetic sensors and sensing application. Sens. Actuators A 1997, 59, 1–8. [Google Scholar] [CrossRef]
- Kurlyandskaya, G.V.; Portnov, D.S.; Beketov, I.V.; Larrañaga, A.; Safronov, A.P.; Orue, I.; Medvedev, A.I.; Chlenova, A.A.; Sanchez-Ilarduya, M.B.; Martinez-Amesti, A.; et al. Nanostructured materials for magnetic biosensing. BBA Gen. Subj. 2017, 1861, 1494–1506. [Google Scholar] [CrossRef]
- Feng, Z.; Zhi, S.; Guo, L.; Wei, M.; Zhou, Y.; Lei, C. A novel integrated microfluidic platform based on micro-magnetic sensor for magnetic bead manipulation and detection. Microfluid. Nanofluid. 2018, 22, 86. [Google Scholar]
- Buznikov, N.A.; Safronov, A.P.; Orue, I.; Golubeva, E.V.; Lepalovskij, V.N.; Svalov, A.V.; Chlenova, A.A.; Kurlyandskaya, G.V. Modelling of magnetoimpedance response of thin film sensitive element in the presence of ferrogel: Next step toward development of biosensor for in-tissue embedded magnetic nanoparticles detection. Biosens. Bioelectron. 2018, 117, 366–372. [Google Scholar] [CrossRef]
- Machado, F.L.A.; de Argoldjo, A.E.P.; Puca, A.A.; Rodrigues, A.R.; Rezende, S.M. Surface magnetoimpedance measurements in soft-ferromagnetic materials. Phys. Status Solidi A 1999, 173, 135. [Google Scholar]
- Kurlyandskaya, G.V.; Vazquez, M.; Munoz, J.L.; García, D.; McCord, J. Effect of induced magnetic anisotropy and domain structure features on magnetoimpedance in stress annealed Co-rich amorphous ribbons. J. Magn. Magn. Mater. 1999, 196, 259–261. [Google Scholar] [CrossRef]
- Chen, L.; Bao, C.C.; Yang, H.; Li, D.; Lei, C.; Wang, T.; Hu, H.Y.; He, M.; Zhou, Y.; Cui, D.X. A prototype of giant magnetoimpedance-based biosensing system for targeted detection of gastric cancer cells. Biosens. Bioelectron. 2011, 26, 3246–3253. [Google Scholar] [CrossRef] [PubMed]
- Ripka, P.; Zaveta, K. Magnetic sensors: Principles and applications. In Handbook of Magnetic Materials; Buschow, K.H.J., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; Volume 18, pp. 347–420. [Google Scholar]
- Kurlyandskaya, G.V.; Barandiaran, J.M.; Vazquez, M.; Garcia, D.; Dmitrieva, N.V. Infuence of geometrical parameters on the giant magnetoimpedance response in amorphous ribbons. J. Magn. Magn. Mater. 2000, 215–216, 740–742. [Google Scholar] [CrossRef]
- Chaturvedi, A.; Dhakal, T.P.; Witanachchi, S.; Le, A.T.; Phan, M.H.; Srikanth, H. Critical length and giant magnetoimpedance in Co69Fe4.5Ni1. 5Si10B15 amorphous ribbons. Mater. Sci. Eng. B 2010, 172, 146–150. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, H.H.; Dong, X.W.; Yan, H.L.; Lei, C.; Luo, Y.S. Giant magnetoimpedance based immunoassay for cardiac biomarker myoglobin. Anal. Methods 2017, 9, 3636–3642. [Google Scholar] [CrossRef]
- Rivero, M.A.; Maicas, M.; López, E.; Aroca, C.; Sánchez, M.C.; Sánchez, P. Influence of the sensor shape on permalloy/Cu/permalloy magnetoimpedance. J. Magn. Magn. Mater. 2003, 254–255, 636–638. [Google Scholar] [CrossRef]
- Yuvchenko, A.A.; Lepalovskii, V.N.; Vas’kovskii, V.O.; Safronov, A.P.; Volchkov, S.O.; Kurlyandskaya, G.V. Magnetic impedance of structured film meanders in the presence of magnetic micro-and nanoparticles. Tech. Phys. 2014, 59, 230–236. [Google Scholar] [CrossRef]
- Lodewijk, K.J.; Fernandez, E.; Garcia-Arribas, A.; Kurlyandskaya, G.V.; Lepalovskij, V.N.; Safronov, A.P.; Kooi, B.J. Magnetoimpedance of thin film meander with composite coating layer containing Ni nanoparticles. J. Appl. Phys. 2014, 115, 17A323. [Google Scholar] [CrossRef]
- Antonov, A.S.; Gadetskii, S.N.; Granovskii, A.B.; D’yachkov, A.L.; Paramonov, V.P.; Perov, N.S.; Prokoshin, A.F.; Usov, N.A.; Lagar’kov, A.N. Giant magnetic impedance in amorphous and nanocrystalline multilayers. Phys. Met. Metall. 1997, 83, 61–71. [Google Scholar]
- Fernández, E.; Lopez, A.; Garcia-Arribas, A.; Svalov, A.V.; Kurlyandskaya, G.V.; Barrainkua, A. High-frequency magnetoimpedance response of thin-film microstructures using coplanar waveguides. IEEE Trans. Magn. 2015, 51, 6100404. [Google Scholar] [CrossRef]
- Vas’kovskii, V.O.; Savin, P.A.; Volchkov, S.O.; Lepalovskii, V.N.; Bukreev, D.A.; Buchkevich, A.A. Nanostructuring effects in soft magnetic films and film elements with magnetic impedance. Tech. Phys. 2013, 58, 105–110. [Google Scholar] [CrossRef]
- Kolding, T.E. A four-step method for de-embedding gigahertz on-wafer CMOS measurements. IEEE Trans. Electron Devices 2000, 47, 734–740. [Google Scholar] [CrossRef]
- Yang, Z.; Lei, J.; Lei, C.; Zhou, Y.; Wang, T. Effect of magnetic field annealing and size on the giant magnetoimpedance in micro-patterned Co-based ribbon with a meander structure. Appl. Phys. A 2014, 116, 1847–1851. [Google Scholar] [CrossRef]
- Handrich, K.; Kobe, S. Amorphe Ferro-and Ferri-Magnetika; PhysikVerlag: Weinheim, Germany, 1980; Mir: Moscow, Rissia, 1982. [Google Scholar]
- Mohri, K.; Uchiyama, T.; Panina, L.V.; Yamamoto, M.; Bushida, K. Recent advances of amorphous wire CMOS IC magneto-impedance sensors: Innovative high-performance micromagnetic sensor chip. J. Sens. 2015, 2015, 718069. [Google Scholar] [CrossRef]
- Hernando, A.; Lopez-Dominguez, V.; Ricciardi, E.; Osiak, K.; Marin, P. Tuned scattering of electromagnetic waves by a finite length ferromagnetic microwire. IEEE Trans. Antennas Propag. 2016, 64, 1112–1115. [Google Scholar] [CrossRef]
- Brzeska, M.; Panhorst, M.; Kamp, P.B.; Schotter, J.; Reiss, G.; Pühler, A.; Becker, A.; Brück, H. Detection and manipulation of biomolecules by magnetic carriers. J. Biotechnol. 2004, 112, 25–33. [Google Scholar] [CrossRef]
- Amalou, F.; Gijs, M.A.M. Giant magnetoimpedance of chemically thinned and polished magnetic amorphous ribbons. J. Appl. Phys. 2001, 90, 3466–3470. [Google Scholar] [CrossRef]
- Kurlyandskaya, G.V.; De Cos, D.; Volchkov, S.O. Magnetosensitive transducers for nondestructive testing operating on the basis of the giant magnetoimpedance effect: A review. Russ. J. Nondestruct. Test. 2009, 45, 377–398. [Google Scholar] [CrossRef]
- Muñoz, J.L.; Kurlyandskaya, G.V.; Barandiarán, J.M.; Potapov, A.P.; Lukshina, V.A.; Vázquez, M. Nonuniform anisotropy and magnetoimpedance in stress annealed amorphous ribbons. Phys. Met. Metall. 2001, 91, S139–S142. [Google Scholar]
- Pirota, K.R.; Kraus, L.; Knobel, M.; Pagliuso, P.G.; Rettori, C. Angular dependence of giant magnetoimpedance in an amorphous Co-Fe-Si-B ribbon. Phys. Rev. B 1999, 60, 6685. [Google Scholar] [CrossRef]
- Yang, Z.; Lei, C.; Zhou, Y.; Sun, X.C. Study on the giant magnetoimpedance effect in micro-patterned Co-based amorphous ribbons with single strip structure and tortuous shape. Microsyst. Technol. 2015, 21, 1995–2001. [Google Scholar] [CrossRef]
- Kurlyandskaya, G.V.; Barandiarán, J.M.; Muñoz, J.L.; Gutierrez, J.; Vazquez, M.; Garcia, D.; Vas’kovskiy, V.O. Frequency dependence of giant magnetoimpedance effect in CuBe/CoFeNi plated wire with different types of magnetic anisotropy. J. Appl. Phys. 2000, 87, 4822–4824. [Google Scholar] [CrossRef]
- Kraus, L. The theoretical limits of giant magneto-impedance. J. Magn. Magn. Mater. 1999, 196–197, 354–356. [Google Scholar] [CrossRef]
- Baselt, D.R.; Lee, G.U.; Natesan, M.; Metzger, S.W.; Sheehan, P.E.; Colton, R.J. A biosensor based on magnetoresistance technology. Biosens. Bioelectron. 1998, 13, 731–739. [Google Scholar] [CrossRef]





| Sample | Number of Turns | Spacing | Width | Length |
|---|---|---|---|---|
| S1 | 3 | 50 µm | 300 µm | 5 mm |
| S2 | 3 | 50 µm | 400 µm | 5 mm |
| S3 | 6 | 40 µm | 250 µm | 5 mm |
| S4 | 6 | 40 µm | 250 µm | 8 mm |
| Sample | S (ΔZ/Z)(%/Oe) | H (Oe) | f (MHz) | S (ΔR/R)(%/Oe) | H (Oe) | f (MHz) |
|---|---|---|---|---|---|---|
| S1 | 14% | 12 | 32 | 15 | 12 | 53 |
| S2 | 12% | 12 | 42 | 14 | 12 | 74 |
| S3 | 9% | 14 | 63 | 10 | 14 | 63 |
| S4 | 36% | 7 | 42 | 36 | 7 | 53 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Chlenova, A.A.; Golubeva, E.V.; Volchkov, S.O.; Guo, P.; Shcherbinin, S.V.; Kurlyandskaya, G.V. Magnetoimpedance Effect in the Ribbon-Based Patterned Soft Ferromagnetic Meander-Shaped Elements for Sensor Application. Sensors 2019, 19, 2468. https://doi.org/10.3390/s19112468
Yang Z, Chlenova AA, Golubeva EV, Volchkov SO, Guo P, Shcherbinin SV, Kurlyandskaya GV. Magnetoimpedance Effect in the Ribbon-Based Patterned Soft Ferromagnetic Meander-Shaped Elements for Sensor Application. Sensors. 2019; 19(11):2468. https://doi.org/10.3390/s19112468
Chicago/Turabian StyleYang, Zhen, Anna A. Chlenova, Elizaveta V. Golubeva, Stanislav O. Volchkov, Pengfei Guo, Sergei V. Shcherbinin, and Galina V. Kurlyandskaya. 2019. "Magnetoimpedance Effect in the Ribbon-Based Patterned Soft Ferromagnetic Meander-Shaped Elements for Sensor Application" Sensors 19, no. 11: 2468. https://doi.org/10.3390/s19112468
APA StyleYang, Z., Chlenova, A. A., Golubeva, E. V., Volchkov, S. O., Guo, P., Shcherbinin, S. V., & Kurlyandskaya, G. V. (2019). Magnetoimpedance Effect in the Ribbon-Based Patterned Soft Ferromagnetic Meander-Shaped Elements for Sensor Application. Sensors, 19(11), 2468. https://doi.org/10.3390/s19112468








