An Analytical Geometry Optimization Model for Current-Mode Cross-Like Hall Plates
Abstract
:1. Introduction
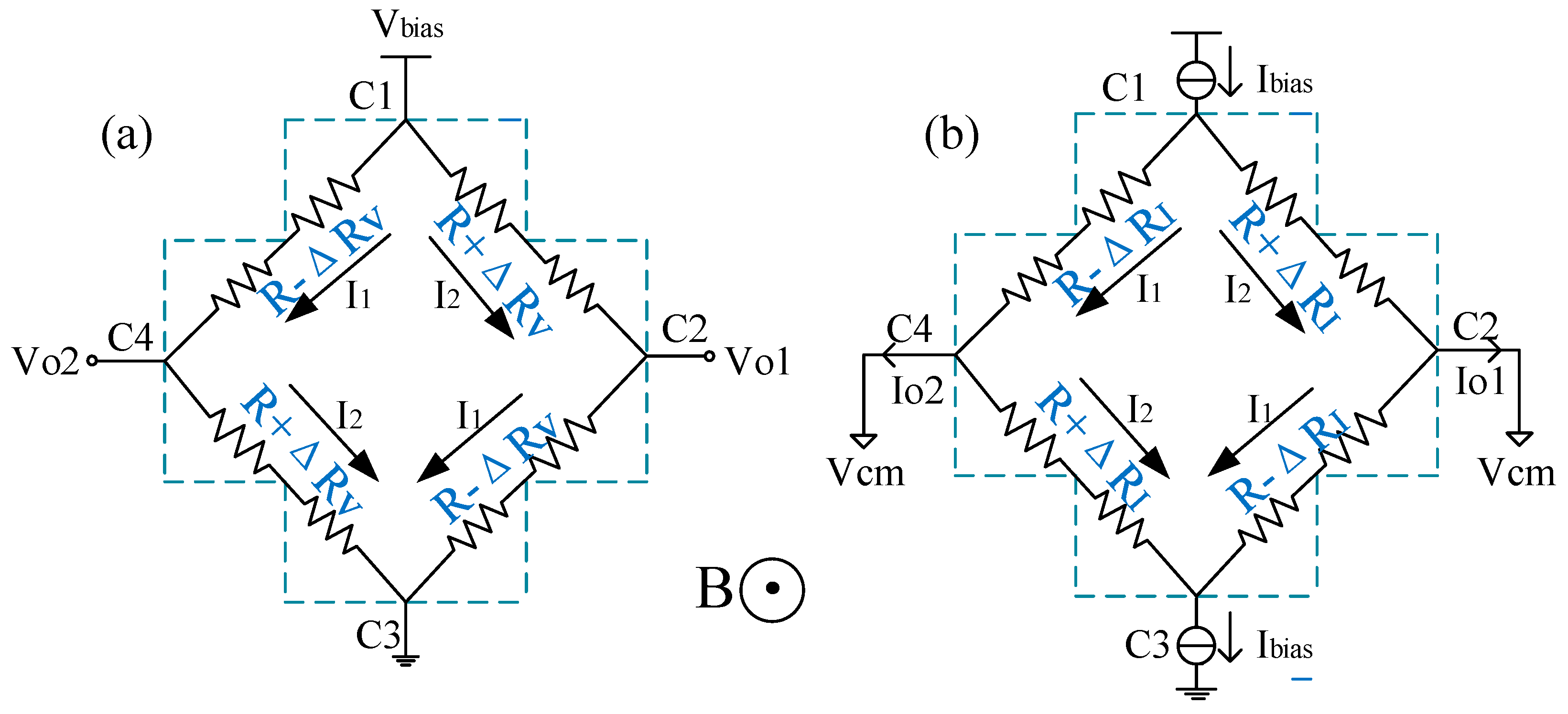
2. Basic Theory of Current-Mode Hall Plate
3. Geometry Optimization Model
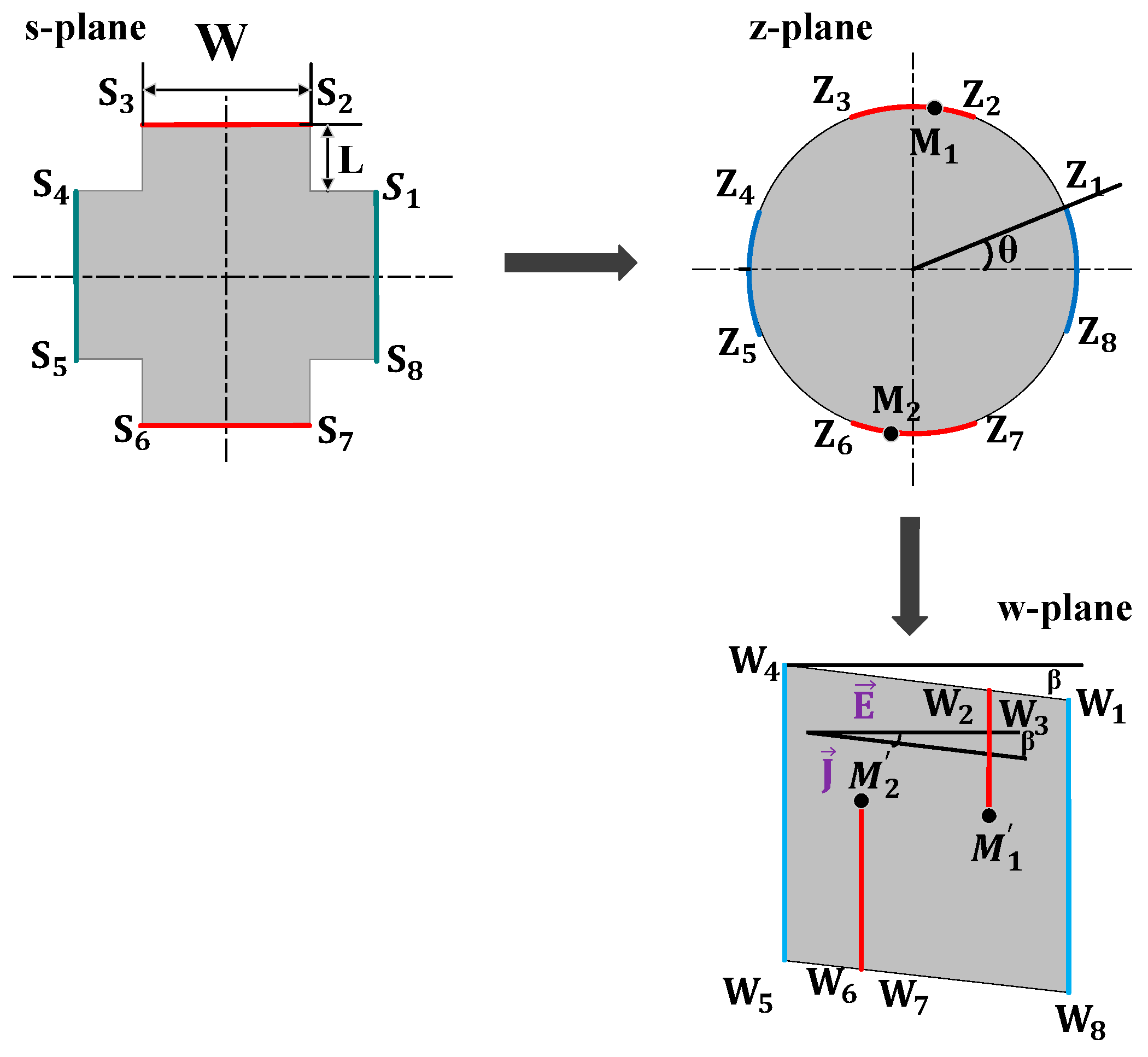
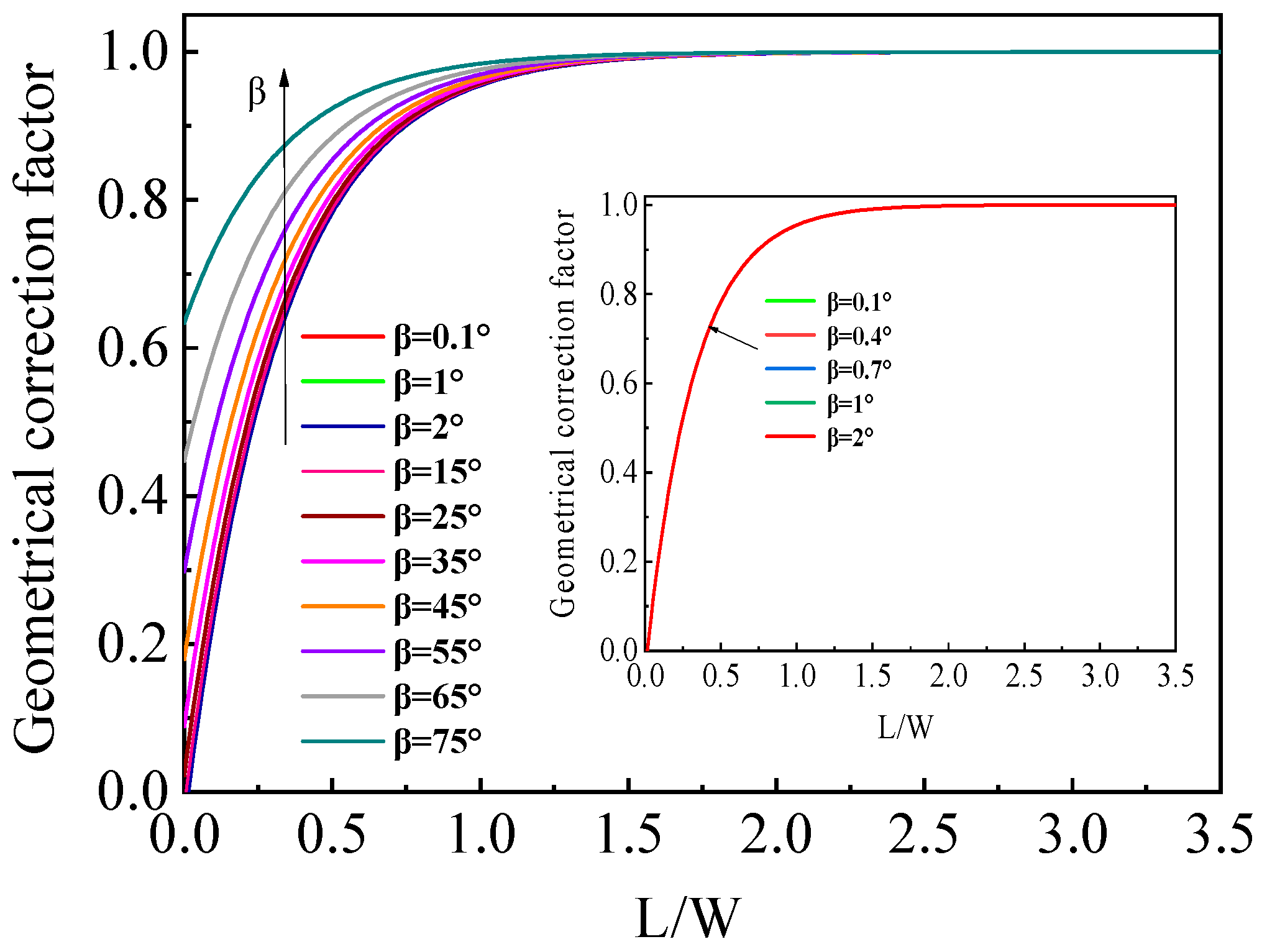
3.1. Conformal Mapping Calculation of Geometrical Correction Factor
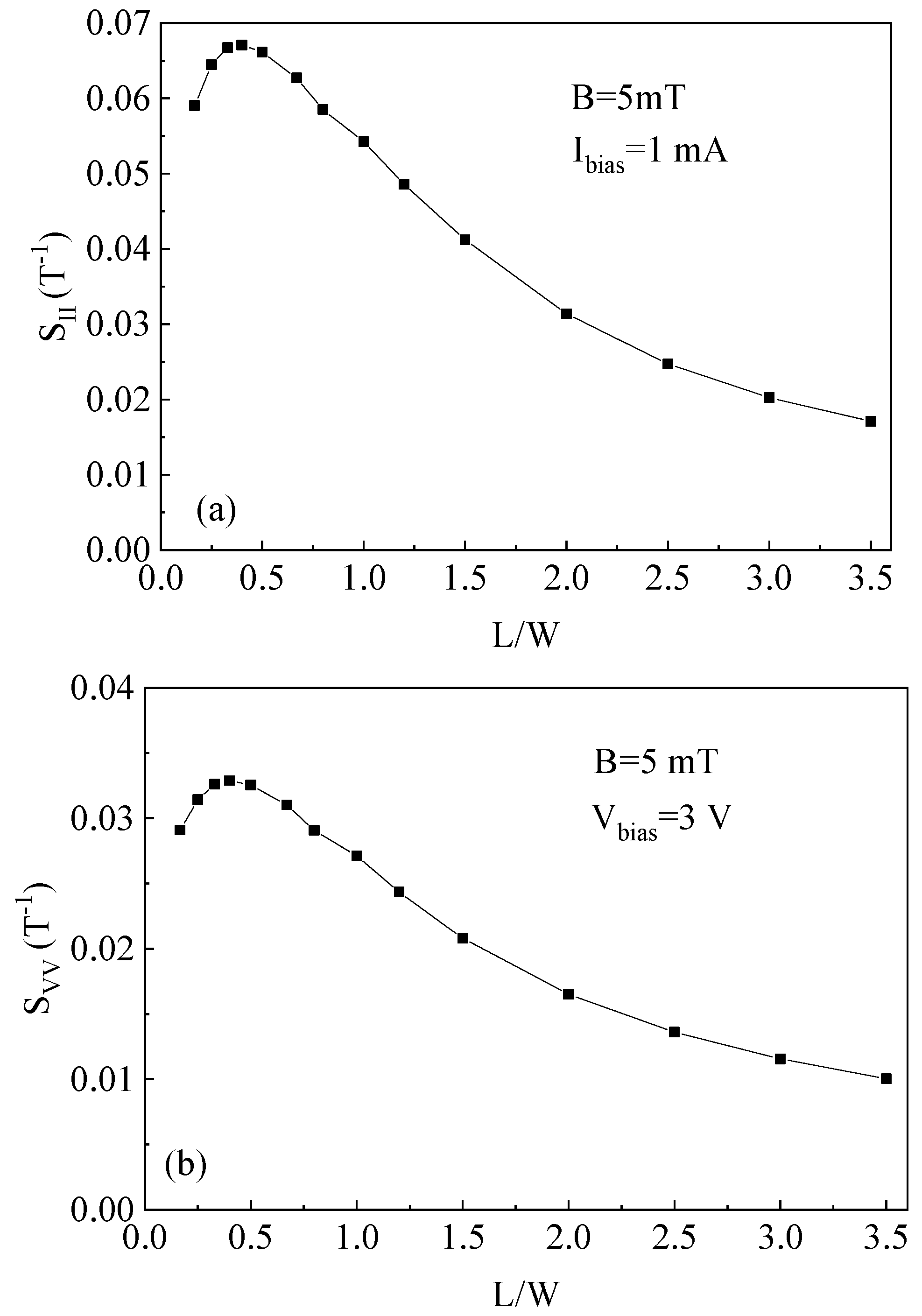
3.2. Optimal Sensitivity
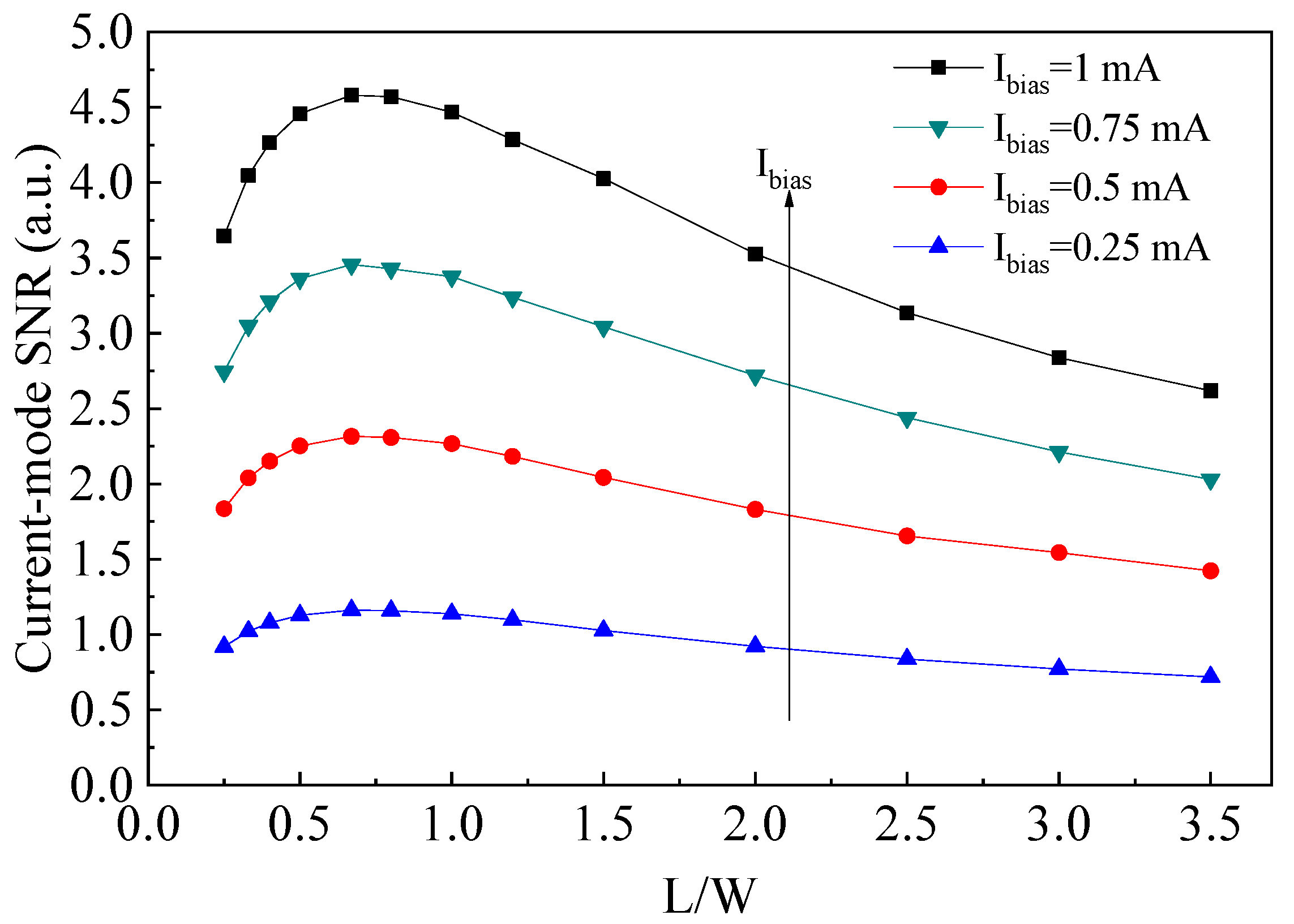
3.3. Optimal Signal-to-Noise Ratio (SNR)
4. TCAD Simulation Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schott, C.; Racz, R.; Manco, A.; Simonne, N. CMOS single-chip electronic compass with microcontroller. IEEE J. Solid State Circuits 2007, 42, 2923–2933. [Google Scholar] [CrossRef]
- Jiang, J.; Makinwa, K. Multipath wide-bandwidth CMOS magnetic sensors. IEEE J. Solid State Circuits 2017, 52, 198–209. [Google Scholar] [CrossRef]
- Weiss, R.; Itzke, A.; Reitenspieß, J.; Hoffmann, I.; Weigel, R. A novel closed loop current sensor based on a circular array of magnetic field sensors. IEEE Sens. J. 2019, 19, 2517–2524. [Google Scholar] [CrossRef]
- Heidari, H.; Gatti, U.; Maloberti, F. Sensitivity characteristics of horizontal and vertical hall sensors in the voltage- and current-mode. In Proceedings of the IEEE Conference on Ph.D. Research Microelectronics and Electronics (PRIME 2015), Glasgow, UK, 29 June–2 July 2015; pp. 330–333. [Google Scholar]
- Heidari, H.; Gatti, U.; Bonizzoni, E.; Maloberti, F. Low-noise low-offset current-mode hall sensors. In Proceedings of the IEEE Conference on Ph.D. Research Microelectronics and Electronics (PRIME 2013), Villach, Austria, 24–27 June 2013; pp. 325–328. [Google Scholar]
- Heidari, H.; Bonizzoni, E.; Gatti, U.; Maloberti, F.; Dahiya, R. Optimal geometry of CMOS voltage-mode and current-mode vertical magnetic hall sensors. In Proceedings of the IEEE Sensors Conference, Busan, Korea, 1–4 November 2015; pp. 1–4. [Google Scholar]
- Heidari, H.; Bonizzoni, E.; Gatti, U.; Maloberti, F. A CMOS current-mode magnetic hall sensor with integrated front-end. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 1270–1278. [Google Scholar] [CrossRef]
- Lyu, F.; Zhang, Z.; Toh, E.H.; Liu, X.; Ding, Y.; Pan, Y.; Pan, H. Performance comparison of cross-like hall plates with different covering layers. Sensors 2014, 15, 672–686. [Google Scholar] [CrossRef] [PubMed]
- Crescentini, M.; Biondi, M.; Romani, A.; Tartagni, M.; Sangiorgi, E. Optimum design rules for CMOS hall sensors. Sensors 2017, 17, 765. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Zhang, J.; Liu, Z.; Wu, P.; Wu, H.; Qian, H.; Wang, Y.; Zhang, Z.; Yu, Z. Geometry optimization of planar hall devices under voltage biasing. IEEE Trans. Electron Devices 2014, 61, 4216–4223. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, M.; Sun, K. Low-frequency noise characterization and signal-to-noise ratio optimization for silicon hall cross sensors. IEEE J. Electron Devices Soc. 2015, 3, 365–370. [Google Scholar] [CrossRef]
- Ausserlechner, U. The signal-to-noise ratio and a hidden symmetry of hall plates. Solid State Electron. 2017, 135, 14–23. [Google Scholar] [CrossRef]
- Xu, Y.; Pan, H. An improved equivalent simulation model for CMOS integrated hall plates. Sensors 2012, 11, 6284–6296. [Google Scholar] [CrossRef] [PubMed]
- Versnel, W. Analysis of the Greek cross, a Van der Pauw structure with finite contacts. Solid State Electron. 1979, 22, 911–914. [Google Scholar] [CrossRef]
- Versnel, W. Analysis of symmetrical hall plates with finite contacts. J. Appl. Phys. 1981, 52, 4659–4666. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, Y.; Guo, Y. Performance prediction of four-contact vertical hall-devices using a conformal mapping technique. J. Semicond. 2015, 36, 124006. [Google Scholar] [CrossRef]
- Versnel, W. Analysis of a circular hall plate with equal finite contacts. Solid State Electron. 1981, 24, 63–68. [Google Scholar] [CrossRef]
- Riccobene, C.; Wachutka, G.; Burgler, J.; Baltes, H. Operating principle of dual collector magnetotransistors studied by two-dimensional simulation. IEEE Trans. Electron Devices 1994, 41, 1136–1148. [Google Scholar] [CrossRef]



| k | αk | φk | k | αk | φk |
|---|---|---|---|---|---|
| 1 | 1/2 + β/π | θ | 5 | 1/2 + β/π | π + θ |
| 2 | 1/2 − β/π | π/2 − θ | 6 | 1/2 − β/π | 3π/2 − θ |
| 3 | 1/2 + β/π | π/2 + θ | 7 | 1/2 + β/π | 3π/2 + θ |
| 4 | 1/2 − β/π | π − θ | 8 | 1/2 − β/π | 2π − θ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Hu, X.; Jiang, L. An Analytical Geometry Optimization Model for Current-Mode Cross-Like Hall Plates. Sensors 2019, 19, 2490. https://doi.org/10.3390/s19112490
Xu Y, Hu X, Jiang L. An Analytical Geometry Optimization Model for Current-Mode Cross-Like Hall Plates. Sensors. 2019; 19(11):2490. https://doi.org/10.3390/s19112490
Chicago/Turabian StyleXu, Yue, Xingxing Hu, and Lei Jiang. 2019. "An Analytical Geometry Optimization Model for Current-Mode Cross-Like Hall Plates" Sensors 19, no. 11: 2490. https://doi.org/10.3390/s19112490
APA StyleXu, Y., Hu, X., & Jiang, L. (2019). An Analytical Geometry Optimization Model for Current-Mode Cross-Like Hall Plates. Sensors, 19(11), 2490. https://doi.org/10.3390/s19112490





