Hybrid Data Fusion DBN for Intelligent Fault Diagnosis of Vehicle Reducers
Abstract
:1. Introduction
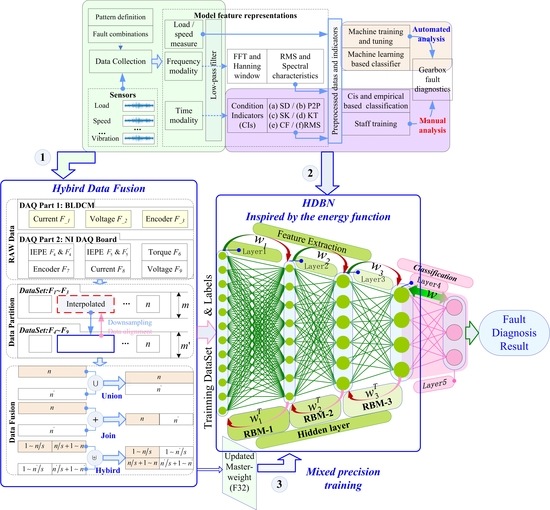
- We have established an efficient fault diagnosis model, namely, HDBN, which is based on an energy perspective that focuses on data fusion for signal analysis and fault diagnosis of rotating devices.
- We explain the significance and role of data (signal) fusion from a physical perspective, and three basic fusion methods are proposed: data union, data join, and data hybrid.
- We present a hybrid precision training algorithm to improve the overall performance of our proposed model without collecting more data.
2. Related Works
3. Methodology
3.1. TSA-Based CI Diagnostic Method from an Energy Perspective
3.2. Basic DBN Model
4. Hybrid Data Fusion and Model Improvement
4.1. Pretreatment
4.2. Hybrid Data Fusion Method
4.3. Mixed-Precision Training
5. Experimental Setup
5.1. Experimental Platform and Fault Seeds
5.2. Data Collection and Segment
5.3. Test Group Setup
6. Results and Analysis
6.1. Results Analysis and Discussion of Different Test Groups
- (1)
- The accuracy was 73.51% in the three types of fusion tests, that is the overall effect of the ⊎ method was the highest.
- (2)
- and worked best in conditions that could be merged. By comparison, the weight of the vibration data from and contributed more than 80%. Other data, such as current and voltage, accounted for less than 3%. In addition, an average increase of 2.04% occurred based on and conversion from and . It is worth noting that mixed precision training contributed an average of 1.88%. Hybrid data fusion and mixed precision training could effectively improve the accuracy of the model without relying on new data.
- (3)
- Figure 15 displays the results of the group test. It can be observed that had the highest accuracy. The accuracy of the difference between and was reduced, although the difference between and was small. The reason was that the accuracy of the model depended more on the number of samples if the total number of samples was not increased, although from a different fusion perspective.
6.2. Results Analysis and Discussion of Different Diagnostic Models
6.3. Results Analysis and Discussion of Fault Prediction
- (1)
- The neural networks with multiple hidden layers can preferably learn representative features from input data. By directly using the RMB algorithm to train multiple hidden layers, HDBN can easily fall into local optima, so that the performance is unstable. This shortcoming occurs because the initial weights and the deviation occurring in the process of error back propagation will affect the stability of neural networks.
- (2)
- Compared with standard neural networks with multiple hidden layers, deep learning consists of two procedures: unsupervised pre-training and supervised fine-tuning. Deep learning can effectively solve the problem of local optima by using unsupervised pre-training layer-by-layer to find the optimal initial weights before fine-tuning these weights.
- (3)
- The diagnostic model based on HDBN can automatically and adaptively learn deep features and the complex nonlinear relevance between the input data of the model and fault patterns. The performance of the model is less dependent on prior knowledge and diagnostic experience.
- (4)
- In the MSE error analysis of fault prediction, HDBN still achieved good performance. However, it should be noted that the error of the above method was large under low speed conditions. The waveform characteristics of the system at higher speeds in the verification system environment were more significant, and the (noise) energy level was also lower, as can be seen from Figure 11 and Figure 12. The effect of noise at low speeds was significant.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| A/D | Analog-to-Digital Converter |
| AC | Alternating Current Power |
| AE | Autoencoder |
| AM-FM | Amplitude Modulation and Frequency Modulation |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| BLDCM | Brushless Direct Current Motor |
| CF | Condition Factor |
| CIs | Condition Indicators |
| CM | Confusion Matrix |
| CNNs | Convolutional Neural Networks |
| COM-CAN | Communication Interface-Controller Area Network Converter |
| CSV | Comma-Separated Values |
| DAE | Denoising Auto-Encoder |
| DAQ | Data Acquisition |
| DBMs | Deep Boltzmann Machines |
| DBN | Deep Belief Network |
| DC | Direct Current Power |
| DL | Deep Learning |
| DNN | Deep Neural Network |
| ELMD | Ensemble Local Mean Decomposition |
| EO | Energy Operator |
| FFT | Fast Fourier Transform |
| FT | Fourier Transform |
| GKPCA | Greedy Kernel Principal Component Analysis |
| HDBN | Hybrid Deep Belief Network |
| IEPE | Integrated Electronics Piezoelectric |
| k-CDM | K-Step Contrastive Divergence Method |
| KT | Kurtosis |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MHMS | Machine Health Monitoring Systems |
| NN | Neural Network |
| P2P | Peak-to-Peak |
| PCA | Principal Component Analysis |
| PGB | Planetary Gearboxes |
| PKFA | Probabilistic Kernel Factor Analysis |
| RMBs | Restricted Boltzmann Machines |
| RMS | Root Mean Square |
| RNNs | Recurrent Neural Networks |
| SAE | Stacked Auto-Encoder |
| SAE-DBN | Sparse Autoencoder-Deep Belief Network |
| SAEs | Sparse Auto-Encoders |
| SCADA | Supervisory Control and Data |
| SD | Standard Deviation |
| SDAs | Stacked Denoising Automatic encoders |
| SK | Skewness |
| TSA | Time Synchronous Averaged |
| WPE | Wavelet Packet Energy |
References
- Lu, C.; Wang, Z.; Qin, W.; Ma, J. Fault diagnosis of rotary machinery components using a stacked denoising autoencoder-based health state identification. Signal Process. 2017, 130, 377–388. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems-Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Yoon, J.; He, D.; Van Hecke, B. On the Use of a Single Piezoelectric Strain Sensor for Wind Turbine Planetary Gearbox Fault Diagnosis. IEEE Trans. Ind. Electron. 2015, 62, 6585–6593. [Google Scholar] [CrossRef]
- Liang, M.; Faghidi, H. Intelligent bearing fault detection by enhanced energy operator. Expert Syst. Appl. 2014, 41, 7223–7234. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.; Miao, Q.; Zhang, X. Time-frequency analysis based on ensemble local mean decomposition and fast kurtogram for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2018, 103, 60–75. [Google Scholar] [CrossRef]
- SaitEmail, A.S.; Sharaf-Eldeen, Y.I. A Review of Gearbox Condition Monitoring Based on vibration Analysis Techniques Diagnostics and Prognostics. In Rotating Machinery, Structural Health Monitoring, Shock and Vibration; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: New York, NY, USA, 2011; pp. 307–324. [Google Scholar]
- Li, K.; Feng, Z.; Liang, X. Planetary Gearbox Fault Diagnosis via Torsional Vibration Signal Analysis in Resonance Region. Shock Vib. 2017, 2017, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Lei, Y.; Lin, J.; Zuo, M.J.; He, Z. Condition monitoring and fault diagnosis of planetary gearboxes: A review. Measurement 2014, 48, 292–305. [Google Scholar] [CrossRef]
- Ng, A. Sparse Autoencoder; Technical report, CS294A Lecture Notes; Stanford University Press: Stanford, CA, USA, 2011; pp. 1–19. [Google Scholar]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Qiao, W.; Lu, D. A Survey on Wind Turbine Condition Monitoring and Fault Diagnosis—Part I: Components and Subsystems. IEEE Trans. Ind. Electron. 2015, 62, 6536–6545. [Google Scholar] [CrossRef]
- Ma, G.; Yang, X.; Zhang, B.; Shi, Z. Multi-feature fusion deep networks. Neurocomputing 2016, 218, 164–171. [Google Scholar] [CrossRef]
- Reddy, K.K.; Sarkar, S.; Venugopalan, V.; Giering, M. Anomaly Detection and Fault Disambiguation in Large Flight Data: A Multi-modal Deep Autoencoder Approach. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, Denver, CO, USA, 18–24 October 2016; pp. 1–8. [Google Scholar]
- Gehring, J.; Miao, Y.; Metze, F.; Waibel, A. Extracting Deep Bottleneck Features Using Stacked Auto-Encoders. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3377–3381. [Google Scholar]
- Wang, H.; Shi, X.; Yeung, D. Relational stacked denoising autoencoder for tag recommendation. In Proceedings of the Twenty-Ninth National Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 3052–3058. [Google Scholar]
- Thirukovalluru, R.; Dixit, S.; Sevakula, R.K.; Verma, N.K.; Salour, A. Generating feature sets for fault diagnosis using denoising stacked auto-encoder. In Proceedings of the 2016 IEEE International Conference on Prognostics and Health Management (ICPHM), Ottawa, ON, Canada, 20–22 June 2016; pp. 1–7. [Google Scholar]
- Serpanos, D.N.; Wolf, M. Industrial Internet of Things; Springer: Berlin, Germany, 2018. [Google Scholar]
- Commerce, M. Internet of Things (IoT) Platforms: Market Outlook and Forecasts 2016–2021. Technical Report, Mind Commerce. 2016. Available online: https://www.rfidjournal.com/store/mc/iot_platforms (accessed on 1 June 2016).
- Commerce, M. Industrial Internet of Things: IIoT Market by Technologies, Solutions and Services 2019–2024. Technical report, Mind Commerce. 2019. Available online: https://www.apnews.com/Business%20Wire/f30c69a7be6748fe90e63d3b5cb32fdd (accessed on 21 May 2019).
- Raj, S. IMF for Bearing Fault Diagnosis. Updated 19 June 2012. Available online: https://ww2.mathworks.cn/matlabcentral/fileexchange/37226-imf-for-bearing-fault-diagnosis?s_tid=FX_rc3_behav (accessed on 19 June 2012).
- Huang, N.E.; Wu, Z.; Long, S.R. Hilbert-Huang transform. Scholarpedia 2008, 3, 2544. [Google Scholar] [CrossRef]
- JIANG, Y. DB-KIT Tools for Data-Driven Process Monitoring, Prognosis and Fault Diagnosis. Updated 8 December 2017. Available online: https://ww2.mathworks.cn/matlabcentral/fileexchange/65348-db-kit (accessed on 25 January 2018).
- Jiang, Y.; Yin, S.; Kaynak, O. Data-Driven Monitoring and Safety Control of Industrial Cyber-Physical Systems: Basics and Beyond. IEEE Access 2018, 6, 47374–47384. [Google Scholar] [CrossRef]
- Jiang, Y.; Yin, S. Recursive Total Principle Component Regression Based Fault Detection and Its Application to Vehicular Cyber-Physical Systems. IEEE Trans. Ind. Inf. 2018, 14, 1415–1423. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B. Support vector machine in machine condition monitoring and fault diagnosis. Mech. Syst. Signal Process. 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Vernekar, K.; Kumar, H.; Gangadharan, K.V. Engine gearbox fault diagnosis using empirical mode decomposition method and Naïve Bayes algorithm. Sadhana-Acad. Proc. Eng. Sci. 2017, 42, 1143–1153. [Google Scholar]
- Phillips, J.; Cripps, E.; Lau, J.W.; Hodkiewicz, M. Classifying machinery condition using oil samples and binary logistic regression. Mech. Syst. Signal Process. 2015, 60, 316–325. [Google Scholar] [CrossRef]
- Lei, Y.; Kong, D.; Lin, J.; Zuo, M.J. Fault detection of planetary gearboxes using new diagnostic parameters. Meas. Sci. Technol. 2012, 23, 055605. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J. Active Steering Actuator Fault Detection for an Automatically-Steered Electric Ground Vehicle. IEEE Trans. Veh. Technol. 2017, 66, 3685–3702. [Google Scholar] [CrossRef]
- Si, J.; Li, Y.; Ma, S. Intelligent Fault Diagnosis for Industrial Big Data. Signal Process. Syst. 2018, 90, 1221–1233. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P. Extracting and composing robust features with denoising autoencoders. In Proceedings of the International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Tao, S.; Zhang, T.; Yang, J.; Wang, X.; Lu, W. Bearing fault diagnosis method based on stacked autoencoder and softmax regression. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 6331–6335. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Chen, Z.; Li, W. Multisensor Feature Fusion for Bearing Fault Diagnosis Using Sparse Autoencoder and Deep Belief Network. IEEE Trans. Instrum. Meas. 2017, 66, 1693–1702. [Google Scholar] [CrossRef]
- Sermanet, P.; Chintala, S.; Lecun, Y. Convolutional neural networks applied to house numbers digit classification. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012), Tsukuba, Japan, 11–15 November 2012; pp. 3288–3291. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Amari, S. Natural gradient works efficiently in learning. Neural Comput. 1998, 10, 251–276. [Google Scholar] [CrossRef]
- Salakhutdinov, R.; Hinton, G.E. Deep Boltzmann Machines. In Proceedings of the 2009 Twelfth International Conference on Artificial Intelligence and Statistics (2009 TICAIS), Clearwater, FL, USA, 16–18 April 2009; pp. 448–455. [Google Scholar]
- Verma, N.K.; Gupta, V.K.; Sharma, M.; Sevakula, R.K. Intelligent condition based monitoring of rotating machines using sparse auto-encoders. In Proceedings of the 2013 IEEE Conference on Prognostics and Health Management (PHM), Gaithersburg, MD, USA, 24–27 June 2013; pp. 1–7. [Google Scholar]
- Li, Z.; Zhang, H.; Mu, D.; Guo, L. Random Time Delay Effect on Out-of-Sequence Measurements. IEEE Access 2016, 4, 7509–7518. [Google Scholar] [CrossRef] [Green Version]
- Junbo, T.; Weining, L.; Juneng, A.; Xueqian, W. Fault diagnosis method study in roller bearing based on wavelet transform and stacked auto-encoder. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 4608–4613. [Google Scholar]
- Ding, X.; He, Q. Energy-Fluctuated Multiscale Feature Learning With Deep ConvNet for Intelligent Spindle Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2017, 66, 1926–1935. [Google Scholar] [CrossRef]
- Khaleghi, B.; Khamis, A.M.; Karray, F.; Razavi, S. Multisensor data fusion: A review of the state-of-the-art. Inf. Fusion 2013, 14, 28–44. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Kong, D. A Method Based on Multi-Sensor Data Fusion for Fault Detection of Planetary Gearboxes. Sensors 2012, 12, 2005–2017. [Google Scholar] [CrossRef] [Green Version]
- Serdio, F.; Lughofer, E.; Pichler, K.; Buchegger, T.; Pichler, M.; Efendic, H. Fault detection in multi-sensor networks based on multivariate time-series models and orthogonal transformations. Inf. Fusion 2014, 20, 272–291. [Google Scholar] [CrossRef]
- Chen, G.; Chen, J.; Zi, Y.; Pan, J.; Han, W. An unsupervised feature extraction method for nonlinear deterioration process of complex equipment under multi dimensional no-label signals. Sens. Actuators A Phys. 2018, 269, 464–473. [Google Scholar] [CrossRef]
- Wang, J.; Xie, J.; Rui, Z.; Mao, K.; Zhang, L. A New Probabilistic Kernel Factor Analysis for Multisensory Data Fusion: Application to Tool Condition Monitoring. IEEE Trans. Instrum. Meas. 2016, 65, 2527–2537. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, H.; Wen, J.; Li, S.; Liu, Q. A deep learning-based recognition method for degradation monitoring of ball screw with multi-sensor data fusion. Microelectron. Reliab. 2017, 75, 215–222. [Google Scholar] [CrossRef]
- Tao, J.; Liu, Y.; Yang, D. Bearing Fault Diagnosis Based on Deep Belief Network and Multisensor Information Fusion. Shock Vib. 2016, 2016, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Wei, D.; Wang, B.; Lin, G.; Liu, D.; Dong, Z.Y.; Liu, H.; Liu, Y. Research on Unstructured Text Data Mining and Fault Classification Based on RNN-LSTM with Malfunction Inspection Report. Energies 2017, 10, 406. [Google Scholar] [CrossRef]
- Jing, L.; Wang, T.; Zhao, M.; Wang, P. An Adaptive Multi-Sensor Data Fusion Method Based on Deep Convolutional Neural Networks for Fault Diagnosis of Planetary Gearbox. Sensors 2017, 17, 414. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, T.P.; Das, S. Multi-sensor data fusion using support vector machine for motor fault detection. Inf. Sci. 2012, 217, 96–107. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, X.; Na, J.; Fung, R.F. Envelope synchronous average scheme for multi-axis gear faults detection. J. Sound Vib. 2016, 365, 276–286. [Google Scholar] [CrossRef]
- Van Hecke, B.; He, D.; Qu, Y. On the Use of Spectral Averaging of Acoustic Emission Signals for Bearing Fault Diagnostics. J. Vib. Acoust. 2014, 136, 061009. [Google Scholar] [CrossRef]
- Qu, Y.; He, D.; Yoon, J.; Bechhoefer, E.; Zhu, J. Gearbox Tooth Cut Fault Diagnostics Using Acoustic Emission and Vibration Sensors—A Comparative Study. Sensors 2014, 14, 1372–1393. [Google Scholar] [CrossRef]
- Bajric, R.; Zuber, N.; Skrimpas, G.A.; Mijatovic, N. Feature Extraction Using Discrete Wavelet Transform for Gear Fault Diagnosis of Wind Turbine Gearbox. Shock Vib. 2016, 2016, 6748469. [Google Scholar] [CrossRef]
- Tran, V.T.; Althobiani, F.; Ball, A. An approach to fault diagnosis of reciprocating compressor valves using Teager-Kaiser energy operator and deep belief networks. Expert Syst. Appl. 2014, 41, 4113–4122. [Google Scholar] [CrossRef]
- Micikevicius, P.; Narang, S.; Alben, J.M.; Diamos, G.; Elsen, E.; Garcia, D.; Ginsburg, B.; Houston, M.; Kuchaiev, O.; Venkatesh, G. Mixed Precision Training. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
















| Pattern Label | Gearbox Condition | Input Speed (RPM) | Load |
|---|---|---|---|
| 1 | Tooth surface wear | 100, 200, 400, 600, 800, 1200, 1400 | Null |
| 2 | Tooth damage (partial) | Null | |
| 3 | Tooth damage (medium) | Null | |
| 4 | Tooth broken (half) | Null | |
| 5 | Broken teeth (overall) | Null | |
| 6 | Normal | Null |
| Input Shaft Speed (RPM) | Output Shaft Speed () | Meshing Frequency () | Sun Gear Fault Frequency () | Planet Gear Fault Frequency () | Ring Gear Fault Frequency () |
|---|---|---|---|---|---|
| 100 | 0.42 | 18.75 | 3.75 | 2.5 | 1.25 |
| 200 | 0.83 | 37.50 | 7.50 | 5.0 | 2.50 |
| 400 | 1.67 | 75.00 | 15.00 | 10.0 | 5.00 |
| 600 | 2.50 | 112.50 | 22.50 | 15.0 | 7.50 |
| 800 | 3.33 | 150.50 | 30.00 | 20.0 | 10.00 |
| 1000 | 4.17 | 187.50 | 37.50 | 30.0 | 12.50 |
| 1200 | 5.00 | 225.00 | 45.00 | 35.0 | 15.00 |
| 1400 | 5.83 | 262.50 | 52.50 | 35.0 | 17.50 |
| Part | Sensor | Feature | Values | Weight | Rate |
|---|---|---|---|---|---|
| (2) | Current | 50 mA | 20 Hz | ||
| (2) | Voltage | 100 mV | |||
| (2) | Encoder | 1000PPR | |||
| (6) | 102 mV/g | 12.5 kHz | |||
| (6) | 98 mV/g | ||||
| (7) | Torque sensor | 0.01 N·m | |||
| (8) | Encoder | 1024 PPR | |||
| (9) | Current | 50 mV/A | |||
| (9) | Voltage | 98.7 mV/V | |||
| (10) | A/D converter | 16 bit |
| Test Group | Grouping Method | Test Group | Grouping Method |
|---|---|---|---|
| Speed (RPM) | (%) | (%) | (%) | (%) | (%) | (%) |
|---|---|---|---|---|---|---|
| 100 | 35.14 | 34.51 | 35.75 | 37.13 | 38.34 | 40.21 |
| 200 | 43.38 | 42.23 | 43.75 | 44.85 | 45.95 | 46.09 |
| 400 | 88.73 | 89.47 | 89.76 | 90.56 | 93.64 | 95.16 |
| 600 | 82.56 | 82.77 | 84.01 | 87.12 | 91.52 | 94.83 |
| 800 | 82.29 | 82.12 | 83.65 | 85.91 | 89.67 | 93.61 |
| 1000 | 79.42 | 78.46 | 79.34 | 83.08 | 87.93 | 88.67 |
| 1200 | 88.78 | 89.47 | 89.73 | 92.67 | 95.59 | 96.13 |
| 1400 | 81.87 | 81.32 | 82.11 | 83.10 | 86.25 | 89.22 |
| average | 72.77 | 72.54 | 73.51 | 75.55 | 78.61 | 80.49 |
| Speed (RPM) | SVM (%) | BPNN (%) | DBN (%) | CNN (%) | HDBN (%) |
|---|---|---|---|---|---|
| 100 | 24.89 | 36.67 | 31.09 | 32.86 | 40.21 |
| 200 | 28.34 | 38.21 | 35.14 | 36.22 | 46.09 |
| 400 | 53.18 | 63.77 | 88.38 | 86.96 | 95.16 |
| 600 | 61.34 | 77.62 | 92.91 | 84.50 | 94.83 |
| 800 | 71.14 | 74.46 | 88.62 | 91.58 | 93.61 |
| 1000 | 68.58 | 77.66 | 82.41 | 91.87 | 88.67 |
| 1200 | 66.96 | 85.19 | 90.81 | 89.99 | 96.13 |
| 1400 | 58.36 | 78.15 | 83.92 | 92.53 | 89.22 |
| average | 54.1 | 66.47 | 74.16 | 75.81 | 80.46 |
| Method | 100 | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 |
|---|---|---|---|---|---|---|---|---|
| DBN | 278.49 | 269.52 | 219.69 | 205.39 | 196.38 | 189.93 | 205.88 | 210.27 |
| AE | 262.76 | 260.77 | 210.38 | 182.38 | 180.24 | 179.2 | 160.89 | 176.13 |
| LSTM | 269.79 | 264.73 | 153.73 | 145.62 | 150.75 | 165.43 | 146.94 | 161.81 |
| CNN | 265.87 | 257.02 | 160.47 | 166.91 | 148.97 | 142.34 | 155.2 | 154.06 |
| HDBN | 248.96 | 243.38 | 146.42 | 147.82 | 146.2 | 152.98 | 143.35 | 160.03 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Li, Z.; Deng, Z.; Hu, B. Hybrid Data Fusion DBN for Intelligent Fault Diagnosis of Vehicle Reducers. Sensors 2019, 19, 2504. https://doi.org/10.3390/s19112504
Zhang T, Li Z, Deng Z, Hu B. Hybrid Data Fusion DBN for Intelligent Fault Diagnosis of Vehicle Reducers. Sensors. 2019; 19(11):2504. https://doi.org/10.3390/s19112504
Chicago/Turabian StyleZhang, Tianfan, Zhe Li, Zhenghong Deng, and Bin Hu. 2019. "Hybrid Data Fusion DBN for Intelligent Fault Diagnosis of Vehicle Reducers" Sensors 19, no. 11: 2504. https://doi.org/10.3390/s19112504
APA StyleZhang, T., Li, Z., Deng, Z., & Hu, B. (2019). Hybrid Data Fusion DBN for Intelligent Fault Diagnosis of Vehicle Reducers. Sensors, 19(11), 2504. https://doi.org/10.3390/s19112504