1. Introduction
The detection of infrared radiation is of great interest for a wide range of applications, such as optical gas sensing in the infrared spectral range. In the atmosphere, there are two windows in the infrared spectral region where the absorption due to water vapor and the scattering due to dust are minimal, which are in the range of 3–5
and 8–14
[
1]. These two transmission windows are of interest for a variety of atmospheric, security and industrial applications with the aim to detect trace concentrations of environmental and toxic gases with sensitivities down to the parts-per-billion range [
2].
Furthermore, the peak emission of the black-body curve for objects at
is around
. This makes the window from 8–14
particularly interesting for detection of human beings and other warm-blooded animals [
1].
There are mainly two types of infrared detectors, quantum (or photon) detectors and thermal detectors (see e.g., [
1,
3,
4]). In photon detectors, radiation is absorbed due to interaction with electrons. The electrical output signal is the result of a change of the electronic energy distribution. The response per unit incident radiation of photon detectors is wavelength dependent. The advantages of photon detectors is the fast response and the excellent signal to noise ratio. The drawback is that these detectors usually require cooling, which makes them bulky, heavy, expensive and inconvenient to use for certain applications. Thermal detectors are based on the principle that incident radiation, which is absorbed, leads to a change of the temperature. The change in temperature leads to a change in some physical property, which is used to generate an electrical signal. The measurement signal depends on the incident radiant power (or on its rate of change) and not on its spectral distribution. However, the absorption of the radiation can be wavelength dependent and provides design constraints. Depending on the type, different effects are measured, such as the change of the electrical resistance in bolometers, the thermoelectric voltage that is created in a thermocouple, or the change of the internal spontaneous polarization in pyroelectric detectors. Thermal detectors usually operate at room temperature. They show a modest sensitivity and slow response. Due to the fact that a temperature change must be induced by the radiation, thermal detectors need to be thermally decoupled from the surroundings. The advantages are that they are cheap and easy to use [
3,
4]. Thanks to specific electrical properties, pyroelectric detectors have found a wide range of applications such as thermovision and remote temperature measurement [
5]. Furthermore, they perform significantly better than photodetectors at wavelengths higher than
when operated at room temperature [
6].
In this work, we investigate a complementary metal–oxide–semiconductor (CMOS) compatible pyroelectric mid-infrared detector for miniaturized gas sensors. Pyroelectricity is defined as the temperature dependence of spontaneous polarization in certain anisotropic solids (see e.g., [
1]). It can only occur in materials that have a unique polar axis, creating a current that is proportional to the change in the temperature of the crystal, rather than the temperature itself. A pyroelectric detector is sensitive to radiation that leads to a change in temperature [
7], meaning that for sensing applications, it is necessary to use a modulated radiation source. Continuous illumination will only generate a signal until the system is thermally stabilized, therefore the detector does not respond to constant illumination. In contrast to thermocouples, pyroelectric detectors are not thermoelectric.
Pyroelectric materials possess permanent electric dipole moments (see e.g., [
1,
7]). This means that dipole moments exist in absence of external electric fields. The associated dipole moment per unit volume is called the spontaneous polarization
. A uniformly polarized region features no net polarization charges within the region but only bound (polarization) surface charges at the boundary of aforesaid region. The spontaneous polarization thus corresponds to a layer of bound charge on each surface of the material. If such materials are exposed to a change in temperature, the net dipole moment and consequently the spontaneous polarization changes (decreases for
and increases for
). If conductive electrodes are attached to the surfaces and are electrically connected, the change of bound charges is compensated by a redistribution of free charges
q from the electrodes, which results in the pyroelectric current
. In one dimension, the pyroelectric coefficient
p is defined as
under the constraints of a constant stress
and a constant electric field
E, respectively [
1]. The pyroelectric short circuit current is,
where
A is the area of the detector and
is the rate of change of temperature (see e.g., [
1,
7]). A pyroelectric material works as charge generator when subject to a homogeneous change in temperature [
7]. Due to the thermal detection approach, pyroelectric detectors only work at low frequencies, which is a disadvantage compared to photon detectors.
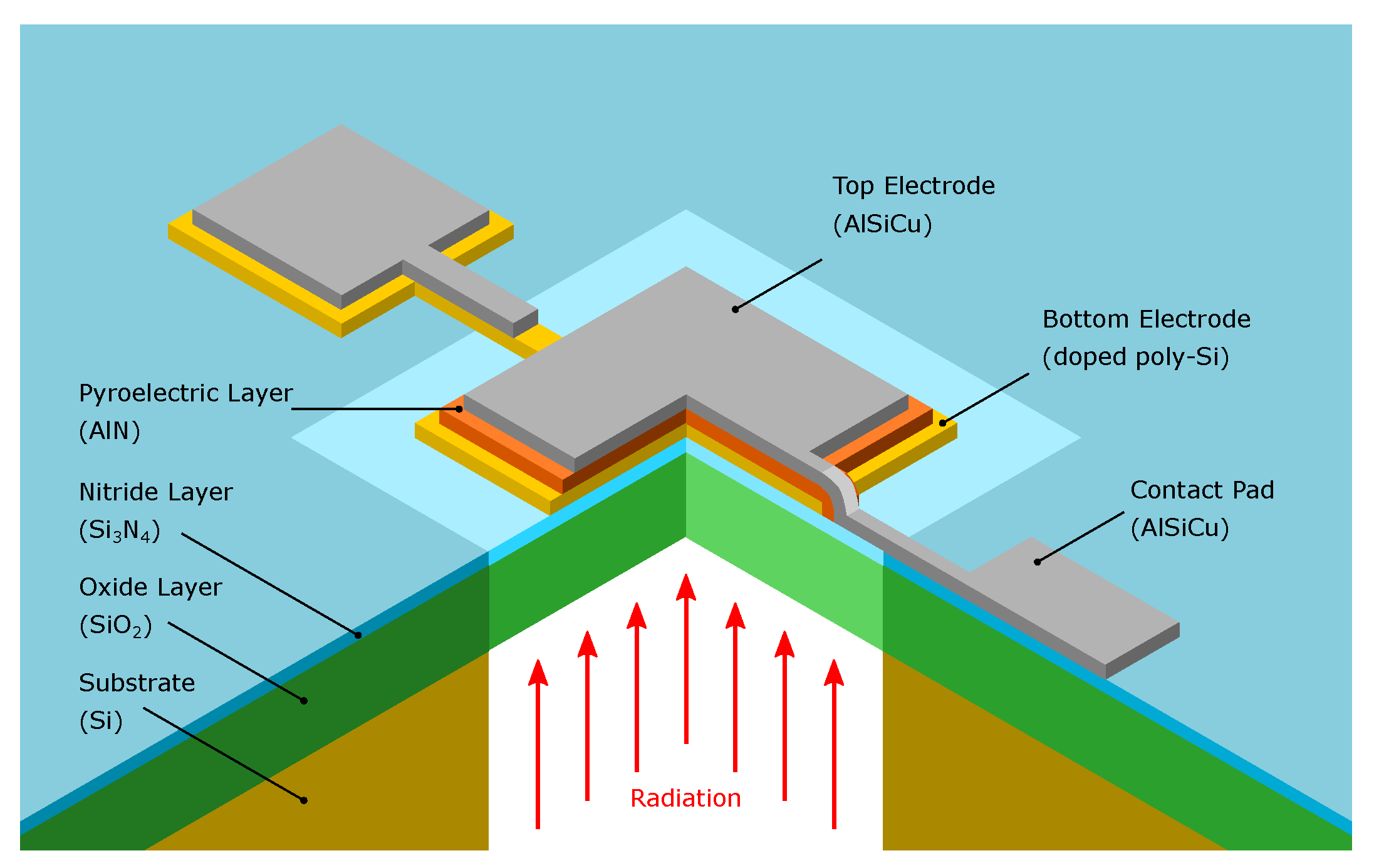
Within this work, aluminium nitride (AlN) grown on poly-Si was used as pyroelectric material. In [
8], a study on the pyroelectric properties grown AlN on
Si was reported. It was shown that the pyroelectric coefficient was practically independent of the temperature and the applied electrical bias and was in the range of
. Furthermore, in [
9] a micromachined infrared detector based on an AlN thin film was demonstrated.
In this work, we describe a CMOS compatible mid-infrared detector based on an AlN thin film specifically to be used in a silicon photonics sensor platform that was presented in [
10,
11]. Our ultimate goal is to fully monolithically integrate a complete optical sensor on a silicon platform. Traditional pyroelectric thermal detectors would not be compatible for this situation, since they usually are designed for free beam illumination from the top, while we expect to couple waveguides to the detector in the same plane. To this aim we developed a novel sensor, using a phosphorous doped-Si layer both as bottom electrode and as infrared absorber. The concept for the fully integrated sensor foresees to have the Si waveguide (not shown in
Figure 1), directly connected to the bottom electrode of the detector, meaning that there is a transition of undoped to doped-Si. This approach allows directly coupling the mode that is propagating in the waveguide to the detector. Due to the metal-like properties of highly doped-Si, the mode which is propagating in the waveguide is absorbed in the doped section, which leads to a temperature rise in the pyroelectric AlN layer. To optimize the performance, we investigated various device dimensions, i.e., various combinations of detector and membrane areas. Furthermore, we determined the noise equivalent power of a devised detector system, comprising our best-in-class detector and a custom readout circuit.
4. Results and Discussion
The topography of the fabricated structures has been investigated using scanning electron microscopy. A micrograph of the bottom-right part and the middle-left part of a detector is shown in
Figure 4a,b, respectively. Due to difficulties during the patterning of the AlN layer, a rough grainy structure of the AlN layer is visible in the areas where it should have been removed. Therefore, residues of AlN are also most probably between the doped-Si contact pad and the AlSiCu layer, which will therefore supposedly influence the contact resistance. This would provide a spurious capacitance in series to the capacitance of the detector, which, however, is not necessarily detrimental for the charge transfer in AC.
When exposed to a modulated radiation, the pyroelectric detector creates a current according to Equation (
2). These experiments were conducted at a wavelength of
, which is just outside of the mid-infrared absorption band of CO
2 in order to avoid an influence of the ambient CO
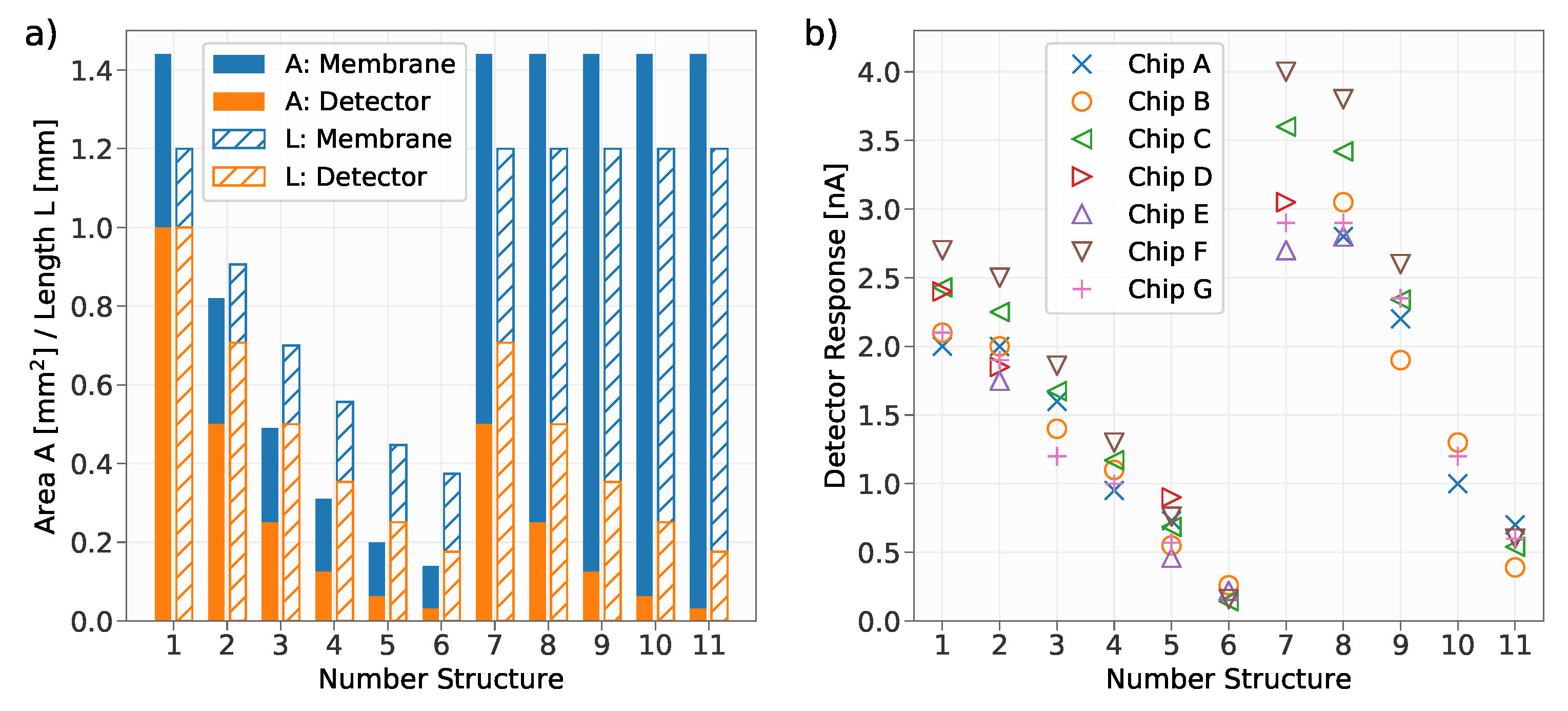
2 concentration. The detector and membrane areas of the investigated structures are shown
Figure 5a. The output current of the detectors was measured using the lock-in amplifier. Each detector was irradiated with a power of
modulated at a frequency of
. The measured current of the detectors is shown in
Figure 5b.
For this investigation, in total seven detector chips (labelled
A to
G) have been characterized. As shown in
Figure 5b, there is some data missing, which is due to the fact that not every detector worked due to failures such as broken detector membranes. It can be observed that the detectors
and
with a detector area of
and
, respectively and a membrane size of
showed the largest response. The measurements show that the highest response, among the tested configurations, can be achieved for detectors with a large membrane area and a small detector area. Obviously, the choice of the irradiated area (i.e., choice of the diameter of the optical fiber and its distance to the detector) also has an influence on the heating of the detector and therefore on the measured current. This effect was not further investigated within this work.
For further investigations, four different detector chips (labelled
H to
K) were used. The experiments described below were conducted using the detector structure
and the readout circuit presented in
Figure 3. The detector response is measured as a voltage. Representative sections of recorded detector response signals to incident radiation
(
,
and
) are shown in
Figure 6a. We note that the optimal modulation frequency (i.e., frequency with highest root mean square (RMS) current output) for the device
was also determined using the experimental setup of the previous experiment and was
. Nevertheless, for these measurements, the chopper which modulates the signal at a frequency of precisely
with a duty cycle of
was used in order to allow for accurate data analysis. Although the modulation frequency of
was too high to reach a steady state of the detector response within the “on” and “off” periods of the QCL, it can be observed that the detector shows the expected response to the rectangular modulated radiation (compare with, e.g., [
5]). The measured voltage changes sign according to the derivative of the temperature (Equation (
2)). A fast Fourier transform (FFT) analysis has been conducted and the lower frequency section of the results is shown in
Figure 6b in units of
, showing the fundamental peak at
. Here also, a measurement of the noise (no incident radiation) is presented. The time domain signals were recorded for
with
. The measurements were conducted for two amplifier boards with two chips (using the chips
J to
G) each, which are identical in design, leading to four measurement configurations. The measurements were performed using three different input radiation powers for each configuration and an additional noise measurement. Each measurement was repeated three times. From the frequency spectrum, the peak value of the amplitude (in units of
) at
was determined for each measurement. The analysis of the power spectral density (PSD) of the noise (the PSD is not plotted in
Figure 6b) between 10 and
shows that the noise behaves as a pink noise with an exponent of
. Beyond
, the noise is roughly flat except for spikes that can be attributed to the environment. The noise in this range is therefore probably dominated by the instrumentation (readout circuit plus oscilloscope). The responsivity of the sensor at
was computed as the ratio
where
and
are the amplitudes of the signal and of the incident power at the fundamental frequency, respectively. The factor
is the first Fourier coefficient of the optical power square wave. The incident power at the fundamental peak can be calculated as
.
Figure 7 shows the amplitude of the signal
versus the incident power for a modulation frequency of
(
). The data was linearly fitted to get the responsivity
. The noise equivalent power (NEP) can be computed from the noise level in a bandwidth of
around
,
and the responsivity
as (see e.g., [
1])
The NEP refers to optical power incident on the pyroelectric detector system and is therefore known as optical NEP [
12]. Furthermore, the detectivity
is defined as
where
A is the area of the detector, which was
for the investigated detector
. The device cut-off frequency was estimated from a simulation of the readout circuit to be
, using the Qucs software. Using the determined parameters, the noise equivalent power of the detector system at
was calculated to be
and the detectivity as
. These parameters correspond to the performance of the investigated demonstrator detector system, meaning the detector together with the readout circuit and furthermore assuming that the whole radiation leaving the optical fiber hits the detector. For comparison, a commercially available detector (Infratec LME-351) which is based on the pyroelectric material lithium-tantalate, reaches a detectivity of
(
) according to the datasheet [
13]. In [
14] a review of CMOS compatible thermopile infrared detectors has been presented, reporting detectvities up to the tens of
range. In [
15] a CMOS compatible n-well microbolometer array with a detectivity of
(
) has been presented. Although the performance of the devised demonstrator devices does not yet reach the performance of previously reported thermopiles and bolometers, nor does it reach the performance of commercially available pyroelectric detectors, the results are very promising. In particular, while the detector was characterized using backside illumination (on the doped poly-Si electrode), we shall keep in mind that in the final scheme the detector will be illuminated from the side using silicon waveguides. If using the bottom electrode as the light absorber is attractive due to the easy integrability with waveguides, the concept comes with limitations in the choice of the absorber material, due to compatibility with the subsequent processes. In contrast to other pyroelectric detectors, absorption does not occur in a very thin (black) metal layer deposited on the top or in complex plasmonic and/or metamaterial absorbers (see e.g., [
7,
16,
17,
18]). As a consequence, the responsivity of the detector is not as high as that of commercial devices. Nevertheless, the concept is particularly promising due to the high integrability with photonics structures, and has the potential to be further extended by using metamaterial designs in order to enhance light absorption at the desired wavelengths. Finally, there is still a margin to improve the performance of the readout electronics.