Indirect Force Control of a Cable-Driven Parallel Robot: Tension Estimation using Artificial Neural Network trained by Force Sensor Measurements
Abstract
:1. Introduction
2. CDPR System
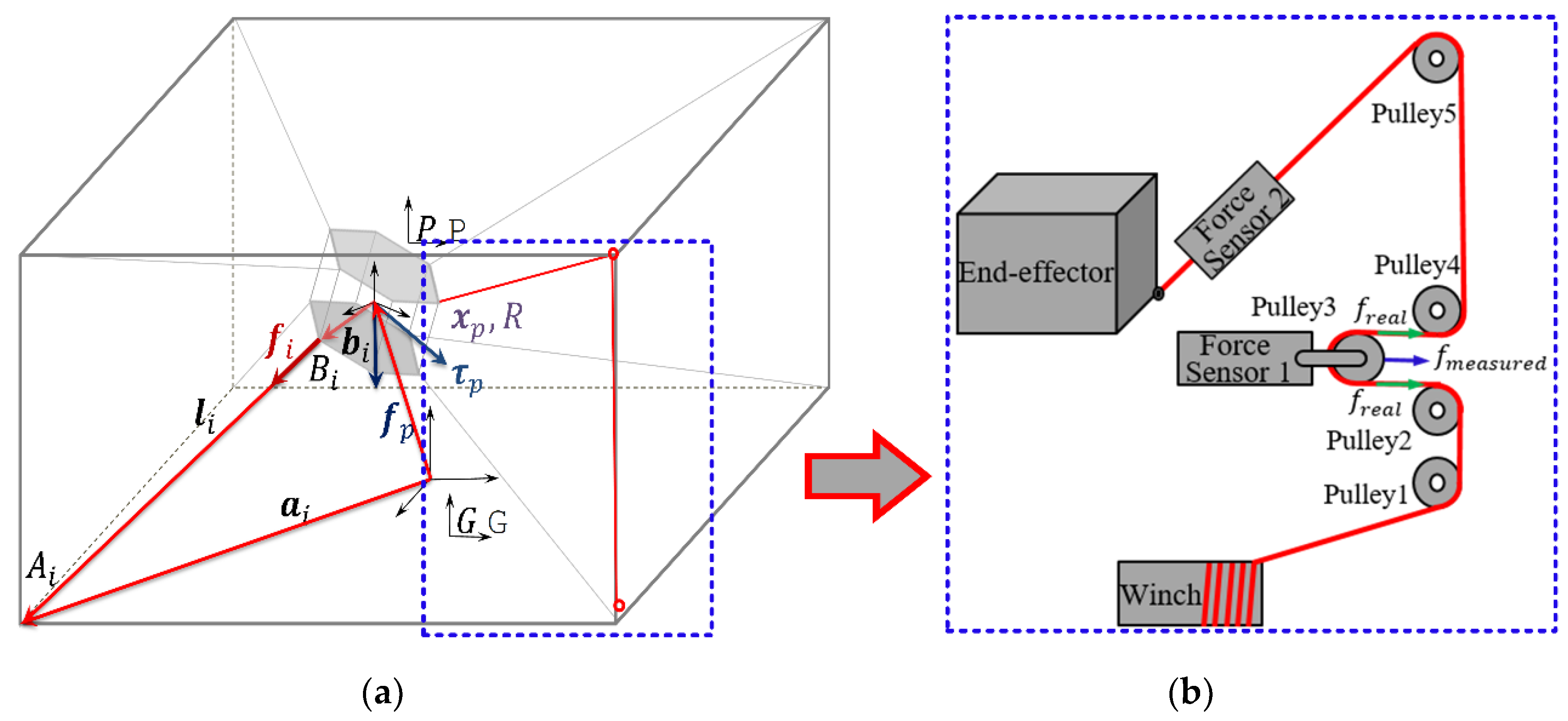
2.1. MINI CDPR
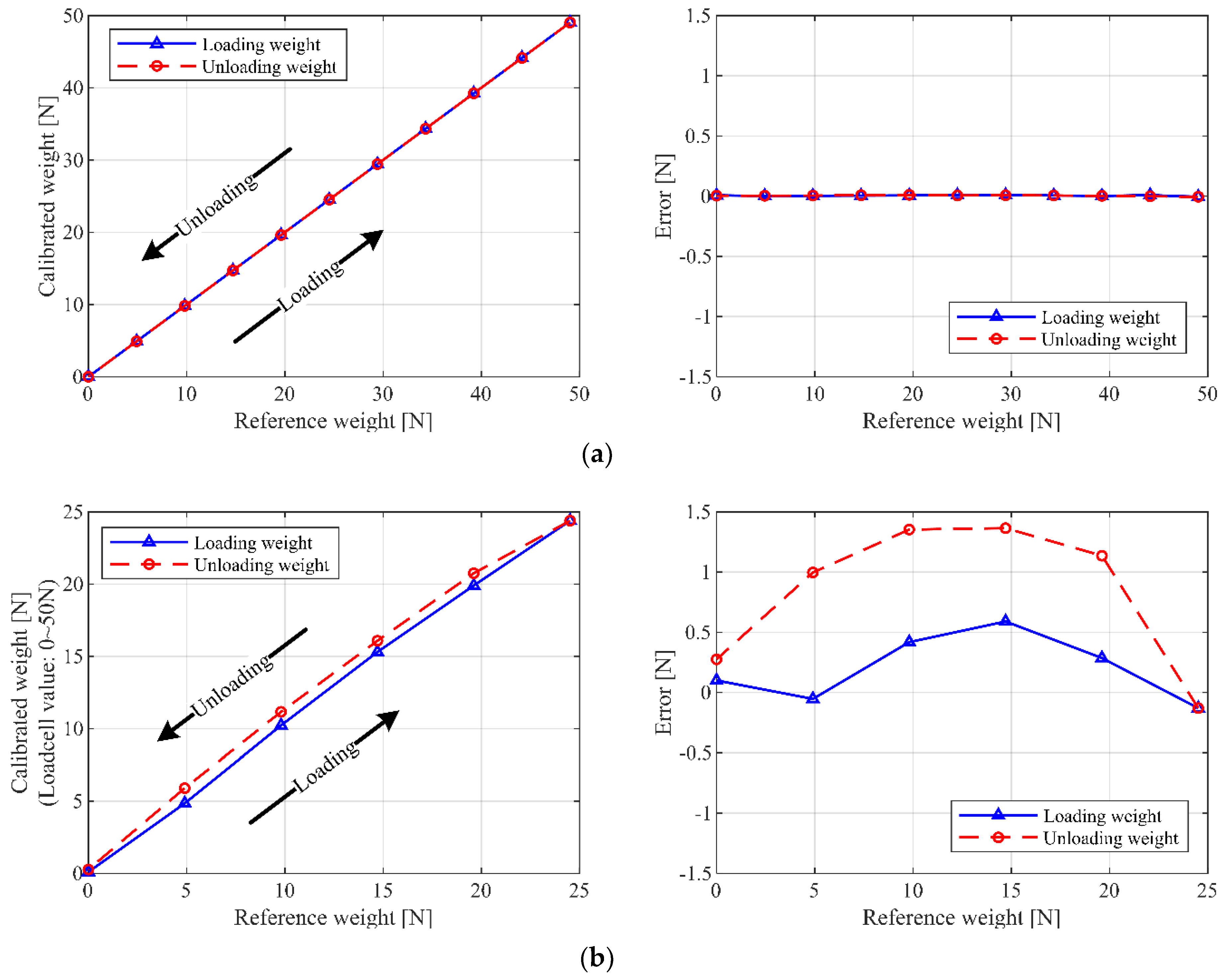
2.2. Force Sensor Calibration
2.3. Kinematics and Dynamics
3. ANN-Based Cable Tension Estimation
3.1. Friction Model Revisited
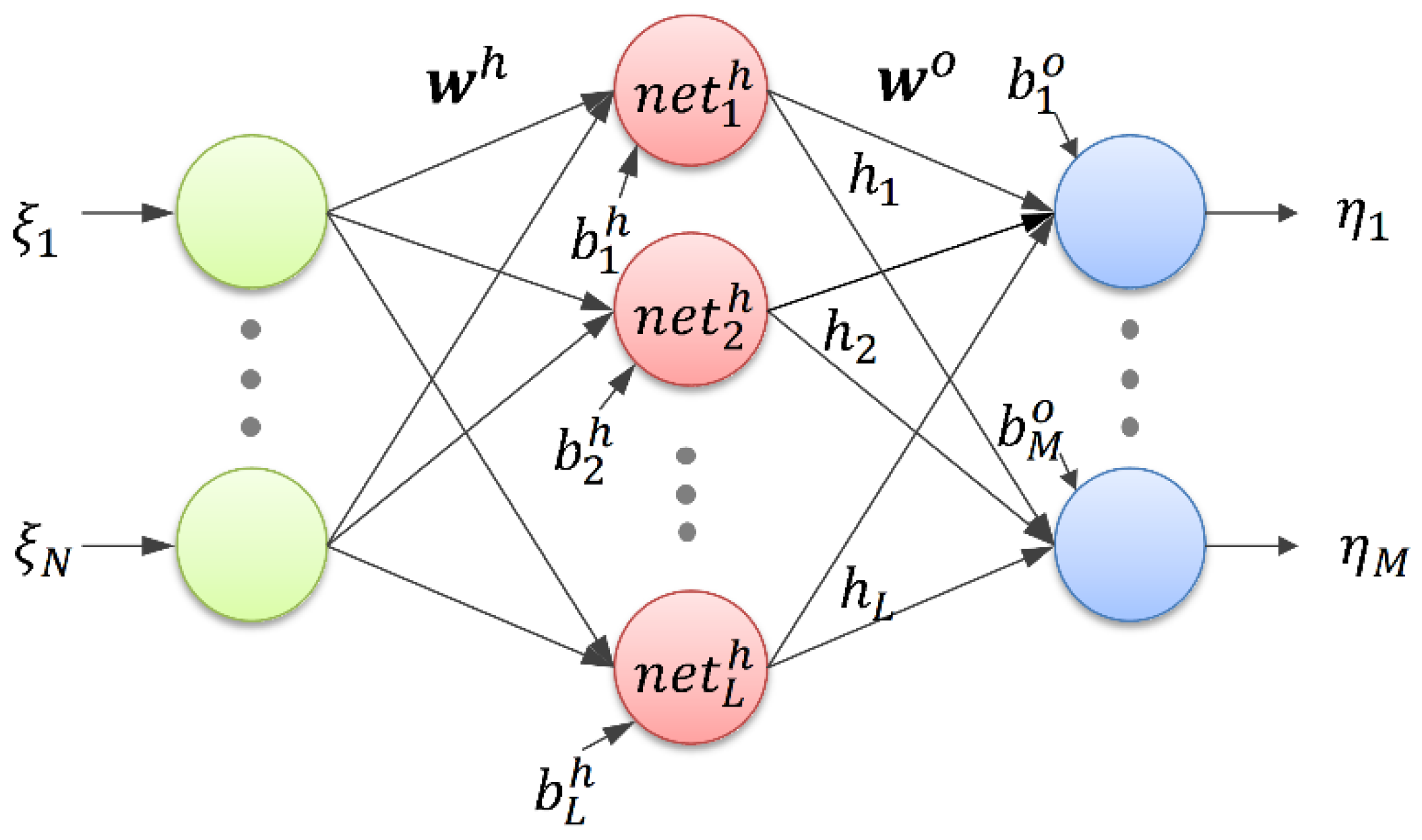
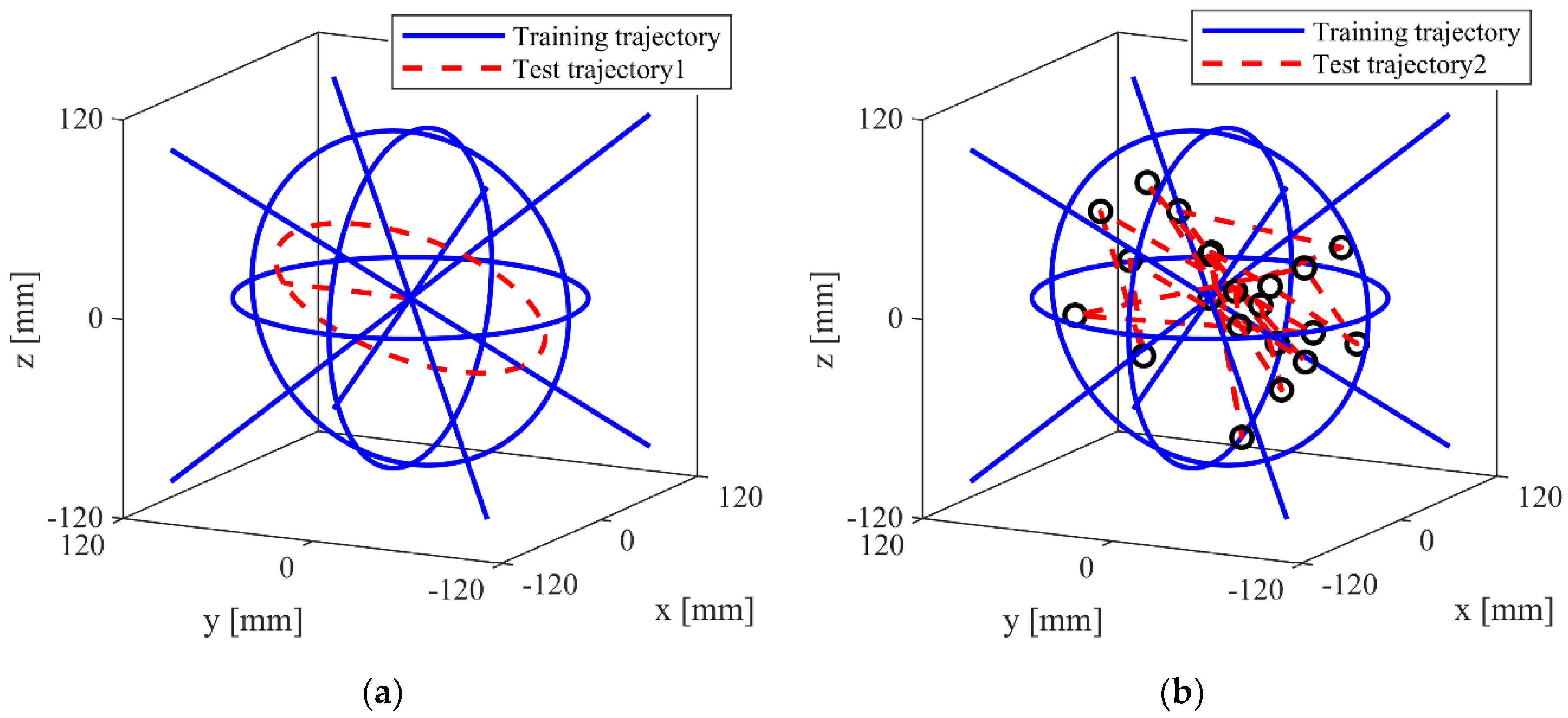
3.2. Designing and Training the ANN
3.3. Performance Evaluation of ANN
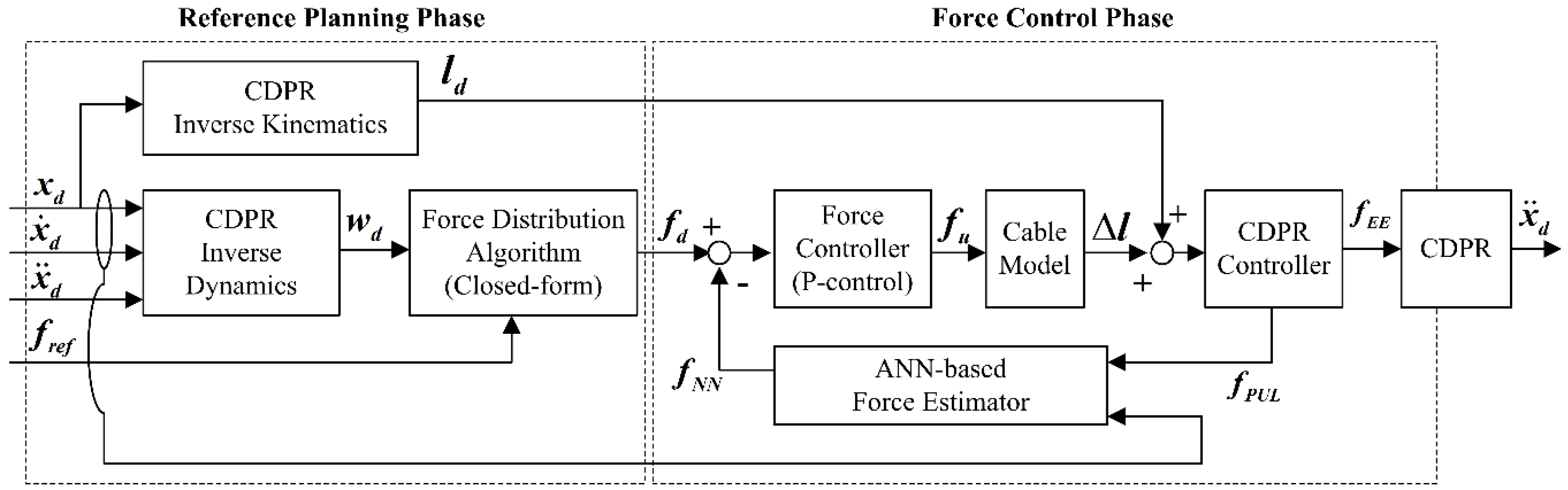
4. End-Effector Force Control
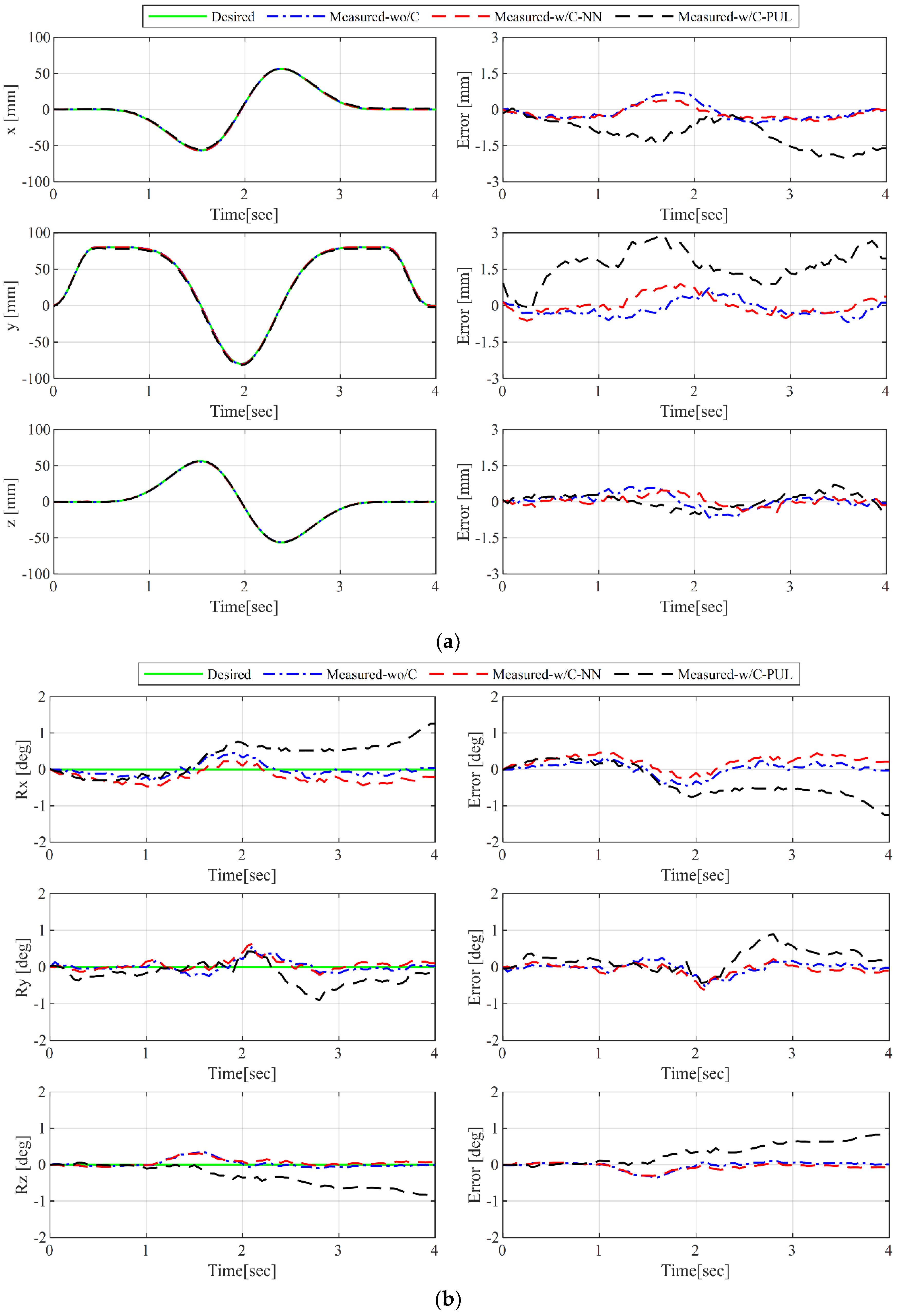
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, H.; Yao, R. Optimal Orientation Planning and Control Deviation Estimation on FAST Cable-Driven Parallel Robot. Adv. Mech. Eng. 2014, 6, 716097. [Google Scholar] [CrossRef]
- Qian, S.; Bao, K.; Zi, B.; Wang, N. Kinematic Calibration of a Cable-Driven Parallel Robot for 3D Printing. Sensors 2018, 18, 2898. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Qiu, Y.; Liu, P. Optimal Cable Tension Distribution of the High-Speed Redundant Driven Camera Robots Considering Cable Sag and Inertia Effects. Adv. Mech. Eng. 2014, 6, 729020. [Google Scholar] [CrossRef]
- Abbasnejad, G.; Eden, J.; Lau, D. Generalized Ray-Based Lattice Generation and Graph Representation of Wrench-Closure Workspace for Arbitrary Cable-Driven Robots. IEEE Trans. Robot. 2019, 35, 147–161. [Google Scholar] [CrossRef]
- Song, D.; Zhang, L.; Xue, F. Configuration Optimization and a Tension Distribution Algorithm for Cable-Driven Parallel Robots. IEEE Access 2018, 6, 33928–33940. [Google Scholar] [CrossRef]
- Gouttefarde, M.; Lamaury, J.; Reichert, C.; Bruckmann, T. A Versatile Tension Distribution Algorithm for n-DOF Parallel Robots Driven by n+2 Cables. IEEE Trans. Robot. 2015, 31, 1444–1457. [Google Scholar] [CrossRef]
- Pott, A.; Bruckmann, T.; Mikelsons, L. Closed-form Force Distribution for Parallel Wire Robots. In Computational Kinematics; Springer: Berlin, Germany, 2009; pp. 25–34. [Google Scholar]
- Kraus, W.; Schmidt, V.; Rajendra, P.; Pott, A. System identification and cable force control for a cable-driven parallel robot with industrial servo drives. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 5921–5926. [Google Scholar]
- Jun, J.; Jin, X.; Pott, A.; Park, S.; Park, J.-O.; Ko, S.Y. Hybrid position/force control using an admittance control scheme in Cartesian space for a 3-DOF planar cable-driven parallel robot. Int. J. Control Autom. Syst. 2016, 14, 1106–1113. [Google Scholar] [CrossRef]
- Xiong, H.; Diao, X. Cable tension control of cable-driven parallel manipulators with position-controlling actuators. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 1763–1768. [Google Scholar]
- Kraus, W.; Kessler, M.; Pott, A. Pulley friction compensation for winch-integrated cable force measurement and verification on a cable-driven parallel robot. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1627–1632. [Google Scholar]
- Choi, S.-H.; Park, J.-O.; Park, K.-S. Tension analysis of a 6-degree-of-freedom cable-driven parallel robot considering dynamic pulley bearing friction. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Peng, Y.; Wei, Y.; Zhou, M. Efficient modeling of cable-pulley system with friction based on arbitrary-Lagrangian-Eulerian approach. Appl. Math. Mech. 2017, 38, 1785–1802. [Google Scholar] [CrossRef]
- Miyasaka, M.; Matheson, J.; Lewis, A.; Hannaford, B. Measurement of the cable-pulley Coulomb and viscous friction for a cable-driven surgical robotic system. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 804–810. [Google Scholar]
- Yu, L.; Wang, Z.; Wang, W.; Li, H.; Wang, L. Research on micromanipulator’s clamping force sensing based on static wirerope tension of a surgical robot. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Lee, T.-K.; Kim, C.-Y.; Lee, M.C. Friction analysis according to pretension of laparoscopy surgical robot instrument. Int. J. Precis. Eng. Manuf. 2011, 12, 259–266. [Google Scholar] [CrossRef]
- Xue, R.; Du, Z.; Yan, Z.; Ren, B. An estimation method of grasping force for laparoscope surgical robot based on the model of a cable-pulley system. Mech. Mach. Theory 2019, 134, 440–454. [Google Scholar] [CrossRef]
- Ismaila, T.; Akmeliawati, R.; Salami, M.J.E. Artificial Intelligent Based Friction Modelling and Compensation in Motion Control System. Adv. Mech. 2011, 43–68. [Google Scholar]
- De Araújo, J.M.; de Menezes, J.M.P.; Moura de Albuquerque, A.A.; da Mota Almeida, O.; Ugulino de Araújo, F.M. Assessment and certification of neonatal incubator sensors through an inferential neural network. Sensors 2013, 13, 15613–15632. [Google Scholar] [CrossRef] [PubMed]
- Jung, S. Stability analysis of reference compensation technique for controlling robot manipulators by neural network. Int. J. Control Autom. Syst. 2017, 15, 952–958. [Google Scholar] [CrossRef]
- Shin, J.; Kim, S.; Tsourdos, A. Neural-networks-based Adaptive Control for an Uncertain Nonlinear System with Asymptotic Stability. Int. J. Control Autom. Syst. 2018, 16, 1989–2001. [Google Scholar] [CrossRef]
- Chen, H.-G.; Wang, Y.-H.; Zhang, L.-L. Adaptive Control based on Extended Neural Network for SISO Uncertain Nonlinear Systems. Int. J. Control Autom. Syst. 2018, 16, 27–38. [Google Scholar] [CrossRef]
- Huang, S.; Tan, K.K. Intelligent Friction Modeling and Compensation Using Neural Network Approximations. IEEE Trans. Ind. Electron. 2012, 59, 3342–3349. [Google Scholar] [CrossRef]
- Guo, K.; Pan, Y.; Yu, H. Composite Learning Robot Control with Friction Compensation: A Neural Network-Based Approach. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, F.; Ge, S.S.; Wu, Y.; Mei, X. End-Effector Force Estimation for Flexible-Joint Robots with Global Friction Approximation Using Neural Networks. IEEE Trans. Ind. Inf. 2019, 15, 1730–1741. [Google Scholar] [CrossRef]
- Lin, C.-H. Precision Motion Control of a Linear Permanent Magnet Synchronous Machine Based on Linear Optical-Ruler Sensor and Hall Sensor. Sensors 2018, 18, 3345. [Google Scholar] [CrossRef] [PubMed]
- Echávarri Otero, J.; de la Guerra Ochoa, E.; Chacón Tanarro, E.; Lafont Morgado, P.; Díaz Lantada, A.; Munoz-Guijosa, J.M.; Muñoz Sanz, J.L. Artificial neural network approach to predict the lubricated friction coefficient. Lubr. Sci. 2014, 26, 141–162. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Y.; Liu, L.; Xie, Z. High-accuracy robust adaptive motion control of a torque-controlled motor servo system with friction compensation based on neural network. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 2318–2328. [Google Scholar] [CrossRef]
- Jin, X.; Jung, J.; Ko, S.; Choi, E.; Park, J.-O.; Kim, C.-S. Geometric Parameter Calibration for a Cable-Driven Parallel Robot Based on a Single One-Dimensional Laser Distance Sensor Measurement and Experimental Modeling. Sensors 2018, 18, 2392. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Jung, J.; Piao, J.; Choi, E.; Park, J.-O.; Kim, C.-S. Solving the pulley inclusion problem for a cable-driven parallel robotic system: Extended kinematics and twin-pulley mechanism. J. Mech. Sci. Technol. 2018, 32, 2829–2838. [Google Scholar] [CrossRef]
- Khosravi, M.A.; Taghirad, H. Dynamic analysis and control of cable driven robots with elastic cables. Trans. Can. Soc. Mech. Eng. 2011, 35, 543–557. [Google Scholar] [CrossRef]
- Marques, F.; Flores, P.; Pimenta Claro, J.C.; Lankarani, H.M. A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dyn. 2016, 86, 1407–1443. [Google Scholar] [CrossRef]
- Pott, A. An Improved Force Distribution Algorithm for Over-Constrained Cable-Driven Parallel Robots. In Computational Kinematics; Springer: Dordrecht, The Netherlands, 2014; pp. 139–146. [Google Scholar]




| Mean | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| EE-tension vs. PUL-tension | 1.81 | 2.11 | 2.02 | 2.77 | 1.89 | 1.69 | 1.81 | 1.82 | 1.99 |
| EE-tension vs. NN-tension | 0.82 | 0.46 | 0.42 | 0.65 | 0.34 | 0.44 | 0.64 | 0.30 | 0.51 |
| Mean | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| EE-tension vs. PUL-tension | 1.34 | 1.54 | 1.30 | 1.41 | 1.63 | 1.57 | 1.31 | 1.50 | 1.45 |
| EE-tension vs. NN-tension | 0.52 | 0.51 | 0.65 | 0.48 | 0.38 | 0.67 | 0.36 | 0.73 | 0.54 |
| kp | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.85 | 0.90 |
|---|---|---|---|---|---|---|---|
| RMSE [N] | 0.489 | 0.466 | 0.465 | 0.437 | 0.451 | 0.479 | 0.527 |
| Desired-wrench vs. Measured-wrench | 0.42 | 0.61 | 0.37 | 0.01 | 0.01 | 0.01 |
| Desired-wrench vs. NN-wrench | 0.44 | 0.56 | 0.80 | 0.03 | 0.02 | 0.02 |
| Desired -wrench vs. PUL-wrench | 1.36 | 1.90 | 1.87 | 0.09 | 0.05 | 0.03 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piao, J.; Kim, E.-S.; Choi, H.; Moon, C.-B.; Choi, E.; Park, J.-O.; Kim, C.-S. Indirect Force Control of a Cable-Driven Parallel Robot: Tension Estimation using Artificial Neural Network trained by Force Sensor Measurements. Sensors 2019, 19, 2520. https://doi.org/10.3390/s19112520
Piao J, Kim E-S, Choi H, Moon C-B, Choi E, Park J-O, Kim C-S. Indirect Force Control of a Cable-Driven Parallel Robot: Tension Estimation using Artificial Neural Network trained by Force Sensor Measurements. Sensors. 2019; 19(11):2520. https://doi.org/10.3390/s19112520
Chicago/Turabian StylePiao, Jinlong, Eui-Sun Kim, Hongseok Choi, Chang-Bae Moon, Eunpyo Choi, Jong-Oh Park, and Chang-Sei Kim. 2019. "Indirect Force Control of a Cable-Driven Parallel Robot: Tension Estimation using Artificial Neural Network trained by Force Sensor Measurements" Sensors 19, no. 11: 2520. https://doi.org/10.3390/s19112520
APA StylePiao, J., Kim, E.-S., Choi, H., Moon, C.-B., Choi, E., Park, J.-O., & Kim, C.-S. (2019). Indirect Force Control of a Cable-Driven Parallel Robot: Tension Estimation using Artificial Neural Network trained by Force Sensor Measurements. Sensors, 19(11), 2520. https://doi.org/10.3390/s19112520





