Detection of Single Steel Strand Distribution in Grouting Duct Based on Capacitive Sensing Technique †
Abstract
:1. Introduction
2. Working Principle and Methodology
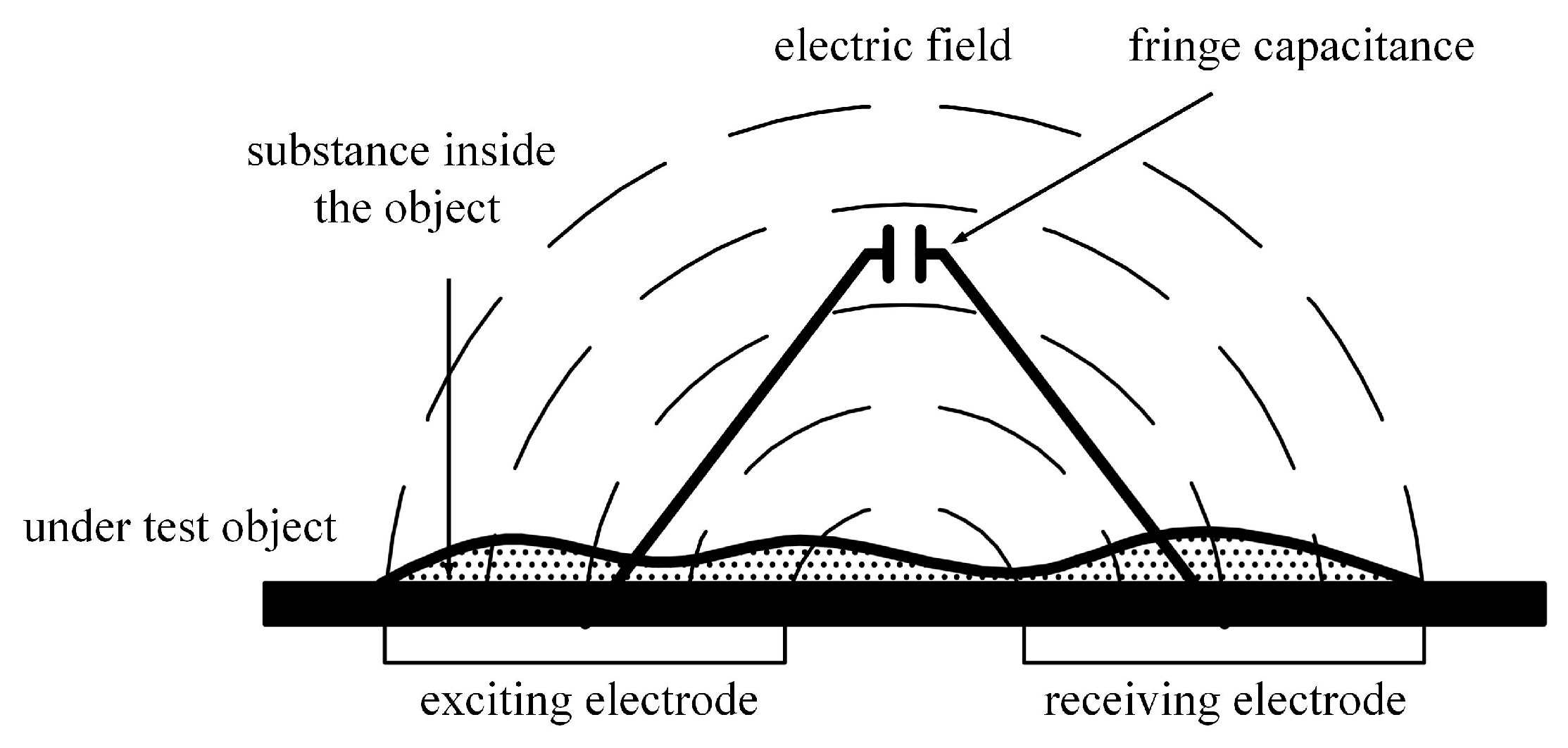
2.1. Working Principle of Capacitive Sensor
2.2. Methodology
3. Simulations and Experiments
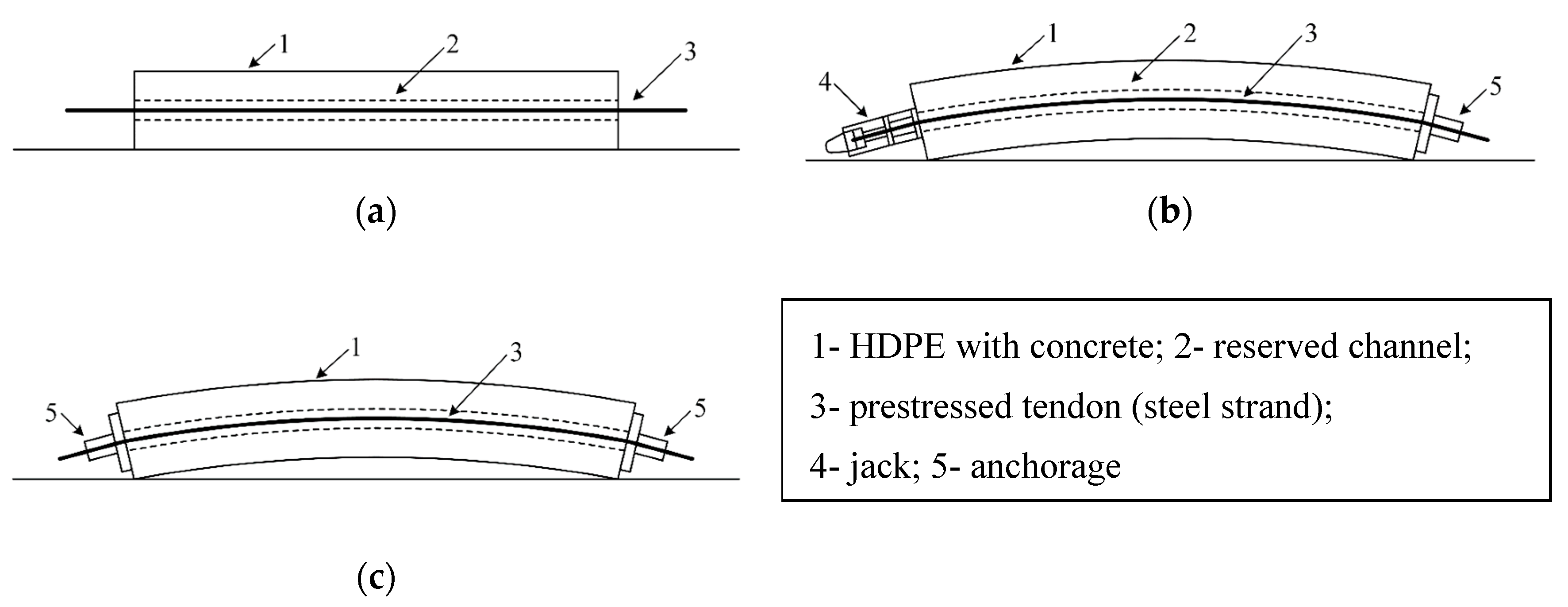
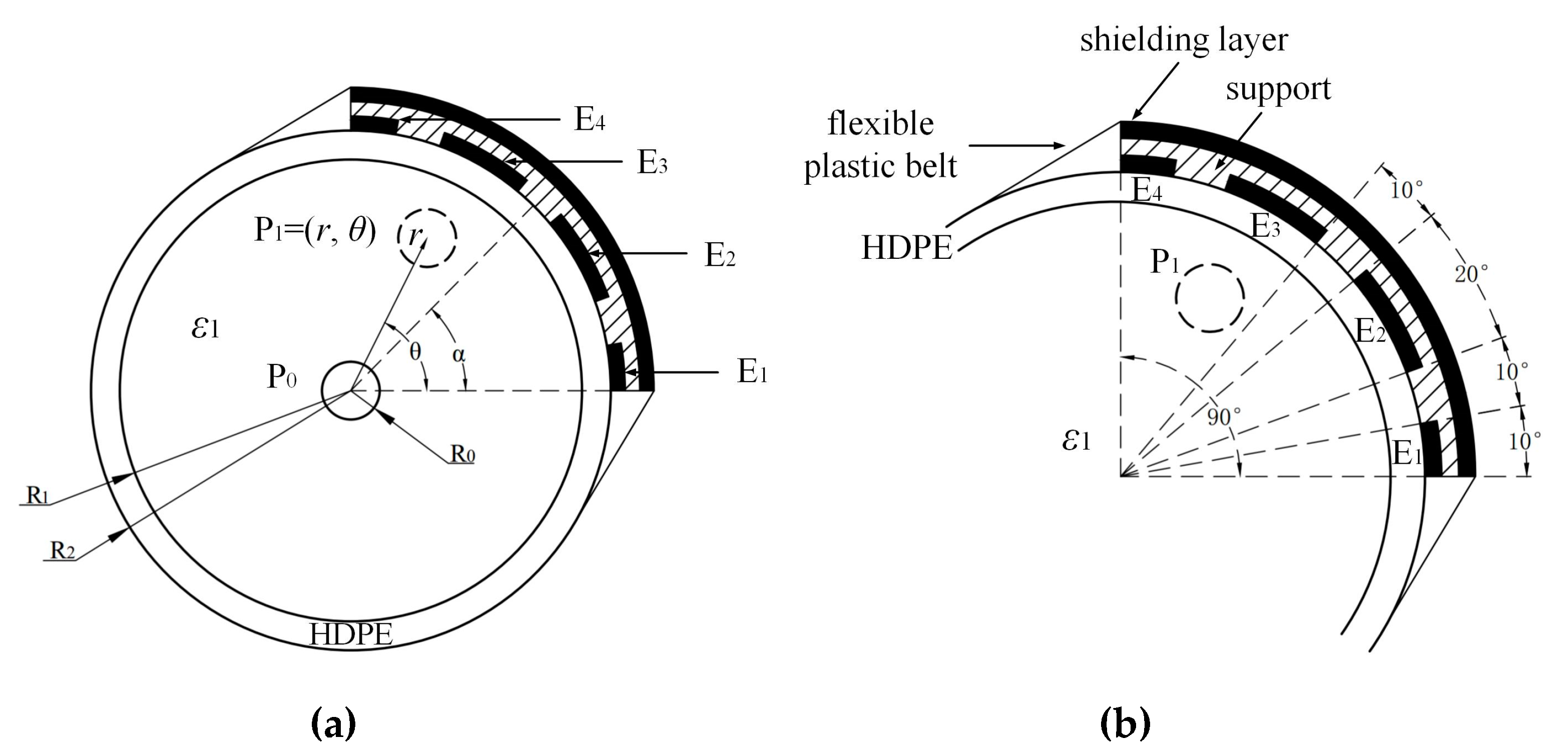
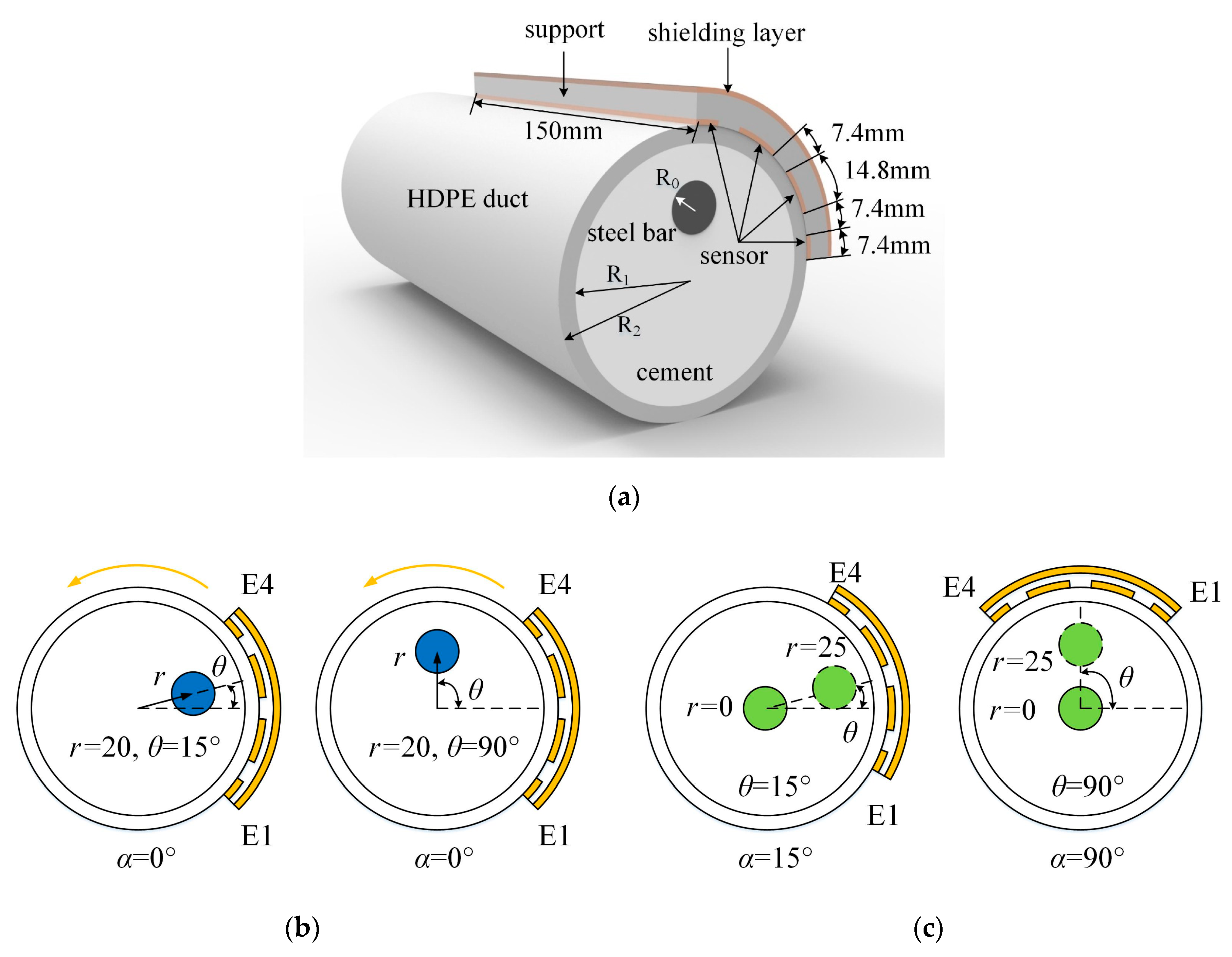
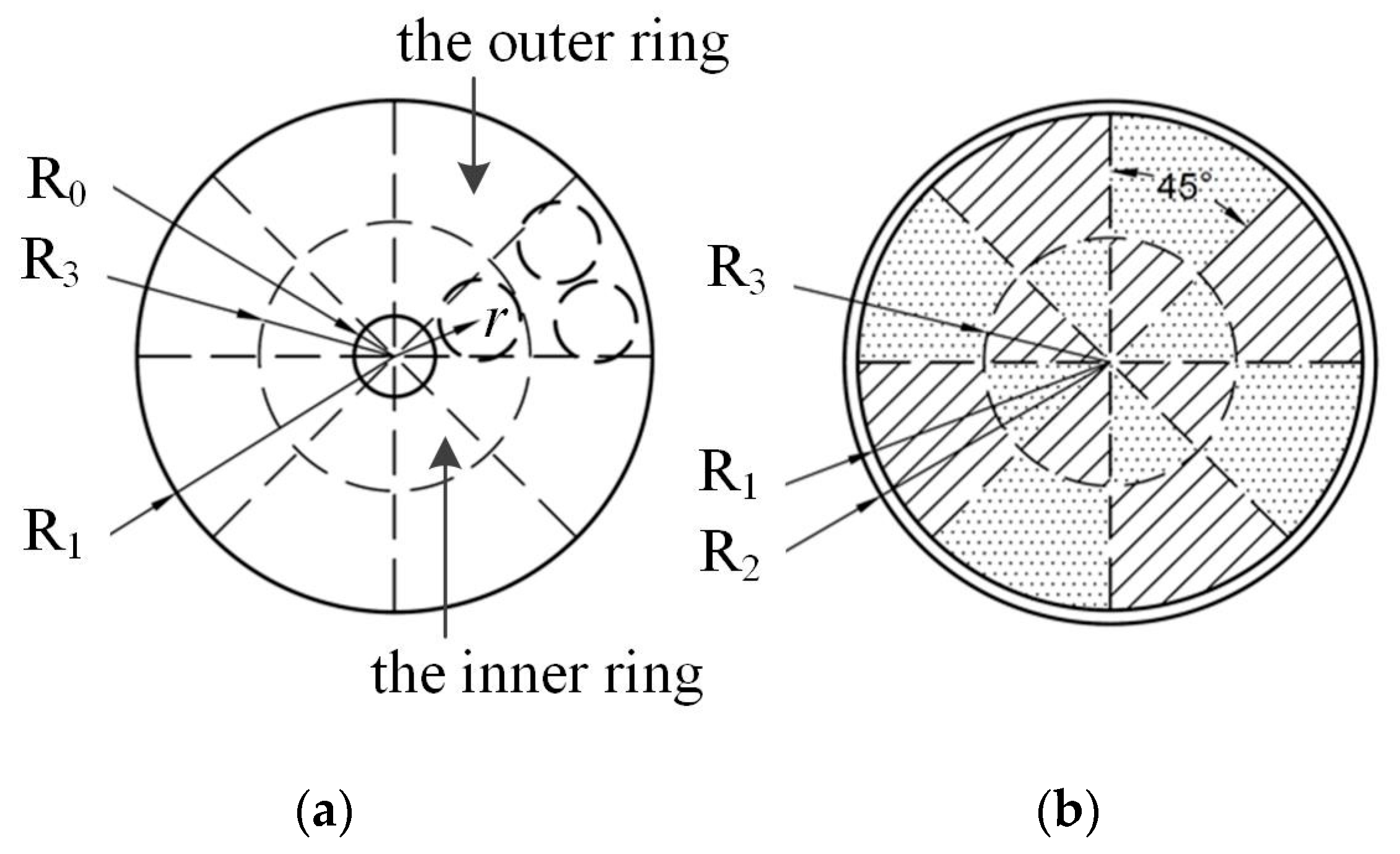
3.1. Phantom and Setup Conditions
3.2. Simulation Results and Analysis
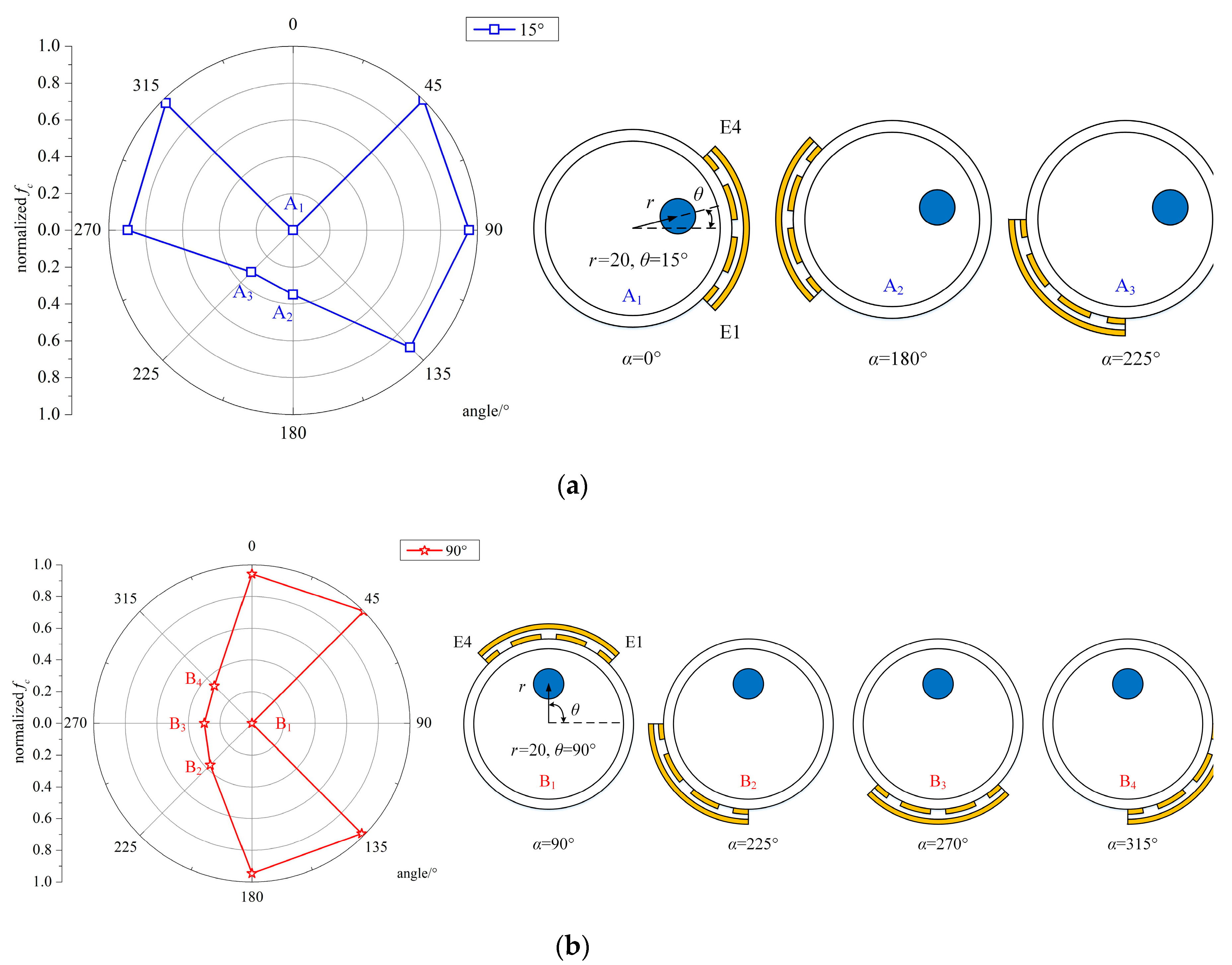
3.2.1. A. Detection of the Angle Position, θ, of the Steel Strand
3.2.2. B. Detection of the Center Distance, r, of the Steel Strand
3.3. Experimental Results and Analysis
3.3.1. A. Detection of the Angular Position, θ, of the Steel Strand
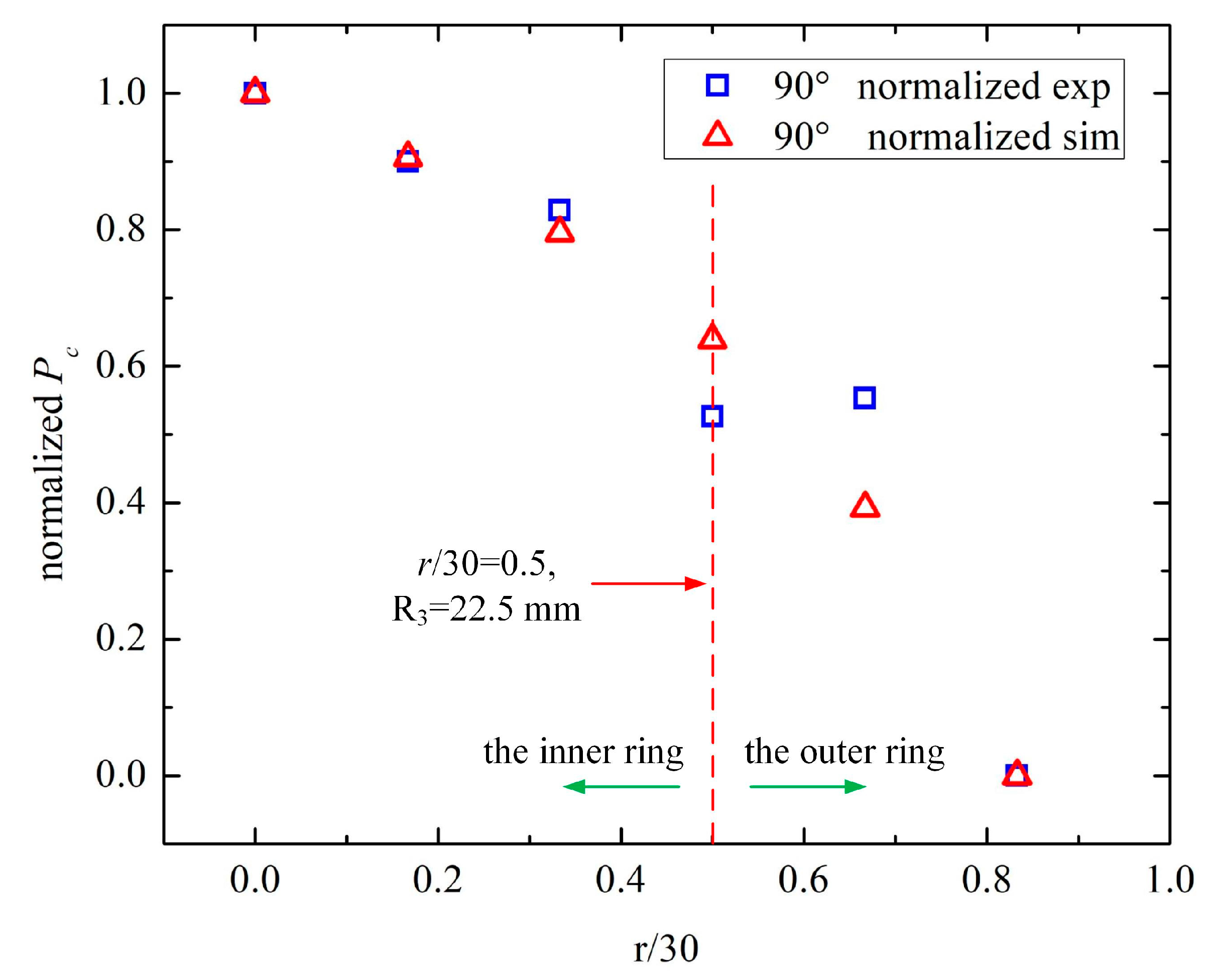
3.3.2. B. Detection of the Center Distance, r, of the Steel Strand
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Martin, J.; Broughton, K.J.; Giannopolous, A.; Hardy, M.S.A.; Forde, M.C. Ultrasonic tomography of grouted duct post-tensioned reinforced concrete bridge beams. NDT E Int. 2001, 34, 107–113. [Google Scholar] [CrossRef]
- Jiang, T.; Kong, Q.; Wang, W.; Huo, L.; Song, G. Monitoring of grouting compactness in a post-tensioning tendon duct using piezoceramic transducers. Sensors 2016, 16, 1343. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Zheng, J.; Huo, L.; Song, G. Finite element analysis of grouting compactness monitoring in a post-tensioning tendon duct using piezoceramic transducers. Sensors 2017, 17, 2239. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, B.J.; Sansalone, M.J.; Poston, R.W. Detecting voids in grouted tendon ducts of post-tensioned concrete structures using the impact-echo method. Struct. J. 1996, 93, 462–473. [Google Scholar]
- Im, S.B.; Hurlebaus, S. Non-destructive testing methods to identify voids in external post-tensioned tendons. KSCE J. Civ. Eng. 2012, 16, 388–397. [Google Scholar] [CrossRef]
- Bore, T.; Placko, D.; Taillade, F.; Himbert, M. Capacitive Sensor for Measuring the Filled of Post-Tensioned Ducts. Experimental Setup, Modeling and Signal Processing. IEEE Sens. J. 2013, 13, 457–465. [Google Scholar] [CrossRef]
- Bore, T.; Placko, D.; Taillade, F.; Sabouroux, P. Electromagnetic characterization of grouting materials of bridge post tensioned ducts for NDT using capacitive probe. NDT E Int. 2013, 60, 110–120. [Google Scholar] [CrossRef]
- Yu, X.; Liu, X.; Chen, S.; Luo, Y.; Wang, X.; Liu, L. High-resolution extended source optical coherence tomography. Opt. Express 2015, 23, 26399–26413. [Google Scholar] [CrossRef]
- Li, N.; Cao, M.; Liu, K.; He, C.; Wu, B. A boundary detecting method for post-tensioned pre-stressed ducts based on Q-factor analysis. Sens. Actuators A-Phys. 2016, 248, 88–93. [Google Scholar] [CrossRef]
- Moustafa, A.; Niri, E.D.; Farhidzadeh, A.; Salamone, S. Corrosion monitoring of post-tensioned concrete structures using fractal analysis of guided ultrasonic waves. Struct. Control Health Monit. 2014, 21, 438–448. [Google Scholar] [CrossRef]
- Sun, Y.; Kang, Y. Magnetic mechanisms of magnetic flux leakage nondestructive testing. Appl. Phys. Lett. 2013, 103, 184104. [Google Scholar] [CrossRef]
- Tan, C.H.; Shee, Y.G.; Yap, B.K.; Adikan, F.M. Fiber Bragg grating based sensing system: Early corrosion detection for structural health monitoring. Sens. Actuators A-Phys. 2016, 246, 123–128. [Google Scholar] [CrossRef]
- Deng, Z.; Kang, Y.; Zhang, J.; Song, K. Multi-source effect in magnetizing-based eddy current testing sensor for surface crack in ferromagnetic materials. Sens. Actuators A-Phys. 2018, 271, 24–36. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Wu, B.; Gao, Z.; He, C. Design of tunnel magnetoresistive-based circular MFL sensor array for the detection of flaws in steel wire rope. J. Sens. 2016, 2016. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, J.; Wu, B.; He, C. A novel sensor to measure the biased pulse magnetic response in steel stay cable for the detection of surface and internal flaws. Sens. Actuators A-Phys. 2018, 269, 218–226. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Liu, L.; Huo, L. Prestress monitoring of a steel strand in an anchorage connection using piezoceramic transducers and time reversal method. Sensors 2018, 18, 4018. [Google Scholar] [CrossRef] [PubMed]
- Hong, X.; Zhou, J.; He, Y. Damage detection of anchored region on the messenger cable based on matching pursuit algorithm. Mech. Syst. Signal Process. 2019, 130, 221–247. [Google Scholar] [CrossRef]
- Xia, R.; Zhou, J.; Zhang, H.; Zhou, D.; Zhang, Z. Experimental Study on Corrosion of Unstressed Steel Strand based on Metal Magnetic Memory. KSCE J. Civ. Eng. 2019, 23, 1320–1329. [Google Scholar] [CrossRef]
- Dang, N.L.; Huynh, T.C.; Kim, J.T. Local Strand-Breakage Detection in Multi-Strand Anchorage System Using an Impedance-Based Stress Monitoring Method—Feasibility Study. Sensors 2019, 19, 1054. [Google Scholar] [CrossRef]
- Zhang, Q.; Xin, R. The defect-length effect in corrosion detection with magnetic method for bridge cables. Front. Struct. Civ. Eng. 2018, 12, 662–671. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of PRC. The Quality Acceptance Specification for Concrete Structure Engineering Construction GB50204-2015; China Architecture & Building Press: Beijing, China, 2015.
- Ministry of Housing and Urban-Rural Development of PRC. External Prestressed Cable Technical Conditions GB/T 30827-2014; China Architecture & Building Press: Beijing, China, 2014.
- Lou, L. Bursting Crack Mechanism of Closure Segment Bottom Slab for the Certain Prestressed Variable Depth Box-section Bridge. Sci. Technol. Rev. 2012, 30, 52–56. [Google Scholar]
- Li, N.; Zhu, H.; Wang, W.; Gong, Y. Parallel double-plate capacitive proximity sensor modelling based on effective theory. AIP Adv. 2014, 4, 027119. [Google Scholar] [CrossRef]
- Li, N.; Yang, X.; Gong, Y.; Wang, P. Enhancing electrical capacitance tomographic sensor design using fuzzy theory based quantifiers. Meas. Sci. Technol. 2014, 25, 125401. [Google Scholar] [CrossRef]
- Li, N.; Cao, M.; He, C.; Wu, B.; Jiao, J.; Yang, X. Multi-parametric indicator design for ECT sensor optimization used in oil transmission. IEEE Sens. J. 2017, 17, 2074–2088. [Google Scholar] [CrossRef]
- Li, X.B.; Larson, S.D.; Zyuzin, A.S.; Mamishev, A.V. Design principles for multichannel fringing electric field sensors. IEEE Sens. J. 2006, 6, 434–440. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of PRC. Code for Application Technique of Cementitious Grout GB/T50448-2015; China Architecture & Building Press: Beijing, China, 2015.





| α/° | Θ = 15°, r = 20 mm | Θ = 90°, r = 20 mm | ||
|---|---|---|---|---|
| C14/pF | Normalized Cn14 | C14/pF | Normalized Cn14 | |
| 0° | 0.015 | 0.057 | 0.594 | |
| 45° | 0.014 | 0.017 | ||
| 90° | 0.044 | 0.016 | ||
| 135° | 0.073 | 0.843 | 0.017 | |
| 180° | 0.084 | 1.000 | 0.057 | 0.594 |
| 225° | 0.080 | 0.943 | 0.077 | 0.884 |
| 270° | 0.067 | 0.757 | 0.085 | 1.000 |
| 315° | 0.028 | 0.200 | 0.077 | 0.884 |
| 360° | 0.015 | 0.014 | 0.057 | 0.594 |
| r/mm | r/30 | 15°(C123) | 15° + 180°(C223) | 15° Pc | 90°(C123) | 90° + 180°(C223) | 90° Pc |
|---|---|---|---|---|---|---|---|
| 0 | 0.000 | 1.218 | 1.212 | 0.501 | 1.205 | 1.209 | 0.499 |
| 5 | 0.167 | 1.168 | 1.246 | 0.484 | 1.155 | 1.244 | 0.482 |
| 10 | 0.333 | 1.095 | 1.272 | 0.463 | 1.083 | 1.269 | 0.460 |
| 15 | 0.500 | 0.986 | 1.291 | 0.433 | 0.974 | 1.288 | 0.431 |
| 20 | 0.667 | 0.823 | 1.306 | 0.386 | 0.812 | 1.303 | 0.384 |
| 25 | 0.833 | 0.599 | 1.319 | 0.312 | 0.589 | 1.316 | 0.309 |
| α/° | θ = 15°, r = 20 mm | θ = 90°, r = 20 mm | ||
|---|---|---|---|---|
| C14/pF | Normalized Cn14 | C14/pF | Normalized Cn14 | |
| 0° | −19 | 1.000 | −28 | 0.583 |
| 45° | −19 | 1.000 | −20 | 0.917 |
| 90° | −27 | 0.652 | −18 | 1.000 |
| 135° | −37 | 0.217 | −20 | 0.917 |
| 180° | −42 | 0.000 | −30 | 0.500 |
| 225° | −40 | 0.087 | −38 | 0.167 |
| 270° | −31 | 0.478 | −42 | 0.000 |
| 315° | −21 | 0.913 | −37 | 0.208 |
| 360° | −19 | 1.000 | −28 | 0.583 |
| α/° | θ = 15°, r = 20 mm | θ = 90°, r = 20 mm | ||
|---|---|---|---|---|
| fc/MHz | Normalized fc | fc/MHz | Normalized fc | |
| 0° | 0.538 | 1.079 | 0.943 | |
| 45° | 1.126 | 1.000 | 1.112 | 1.000 |
| 90° | 1.099 | 0.955 | 0.534 | |
| 135° | 1.066 | 0.898 | 1.102 | 0.982 |
| 180° | 0.743 | 1.081 | 0.946 | |
| 225° | 0.726 | 0.748 | ||
| 270° | 1.065 | 0.897 | 0.707 | |
| 315° | 1.112 | 0.976 | 0.727 | |
| 360° | 0.538 | 0.000 | 1.079 | 0.943 |
| r/mm | r/30 | 90°(C123) | 90°+180°(C223) | 90° Pc |
|---|---|---|---|---|
| 0 | 0.000 | 0.258 | 0.253 | 0.505 |
| 5 | 0.167 | 0.273 | 0.272 | 0.501 |
| 10 | 0.333 | 0.255 | 0.257 | 0.498 |
| 15 | 0.500 | 0.243 | 0.257 | 0.486 |
| 20 | 0.667 | 0.245 | 0.258 | 0.487 |
| 25 | 0.833 | 0.239 | 0.275 | 0.465 |
| r/mm | r/30 | 90° Experiment | 90° Simulation | ||
|---|---|---|---|---|---|
| Pc | Normalized Pc | Pc | Normalized Pc | ||
| 0 | 0.000 | 0.505 | 1.000 | 0.499 | 1.000 |
| 5 | 0.167 | 0.501 | 0.900 | 0.482 | 0.906 |
| 10 | 0.333 | 0.498 | 0.828 | 0.460 | 0.796 |
| 15 | 0.500 | 0.486 | 0.527 | 0.431 | 0.639 |
| 20 | 0.667 | 0.487 | 0.554 | 0.384 | 0.393 |
| 25 | 0.833 | 0.465 | 0.000 | 0.309 | 0.000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Cao, M.; Du, H.; He, C.; Wu, B. Detection of Single Steel Strand Distribution in Grouting Duct Based on Capacitive Sensing Technique. Sensors 2019, 19, 2564. https://doi.org/10.3390/s19112564
Li N, Cao M, Du H, He C, Wu B. Detection of Single Steel Strand Distribution in Grouting Duct Based on Capacitive Sensing Technique. Sensors. 2019; 19(11):2564. https://doi.org/10.3390/s19112564
Chicago/Turabian StyleLi, Nan, Mingchen Cao, Hangben Du, Cunfu He, and Bin Wu. 2019. "Detection of Single Steel Strand Distribution in Grouting Duct Based on Capacitive Sensing Technique" Sensors 19, no. 11: 2564. https://doi.org/10.3390/s19112564
APA StyleLi, N., Cao, M., Du, H., He, C., & Wu, B. (2019). Detection of Single Steel Strand Distribution in Grouting Duct Based on Capacitive Sensing Technique. Sensors, 19(11), 2564. https://doi.org/10.3390/s19112564






