In-Situ Monitoring and Diagnosing for Fused Filament Fabrication Process Based on Vibration Sensors
Abstract
1. Introduction
2. Methodology and Experimental Setup
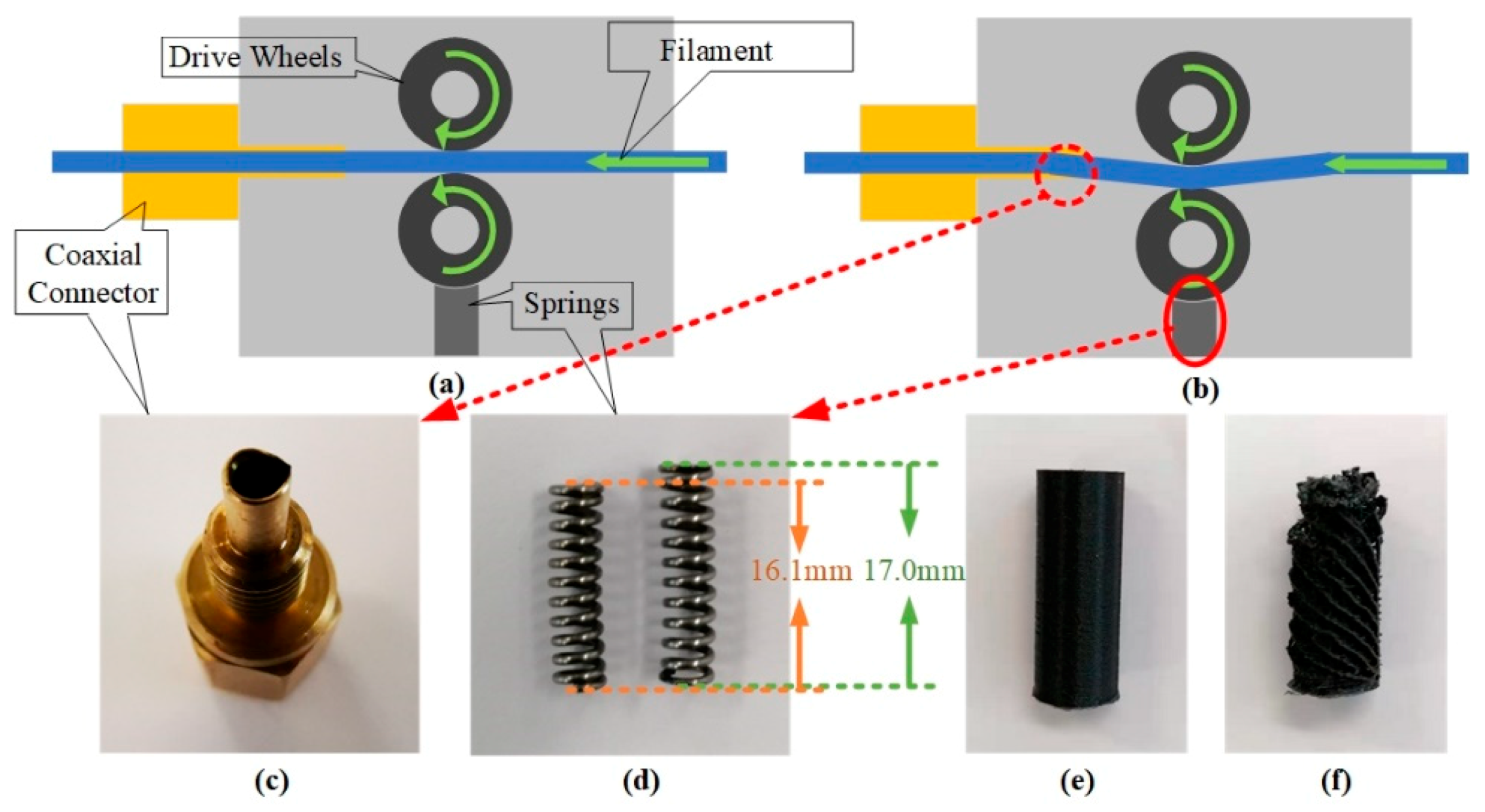
2.1. Experimental Setup
2.2. Vibration Signal Preprocessing
- RMS is proportional to the energy contents of the signal in time domain, whose changes might signify the change of the 3D printer operating states, or it can be related to product defects.
- CF is the ratio of peak-to-valley value to the RMS value of the vibration signal and elucidates any outcome present in the vibration signal [37].
2.3. In-Situ Monitoring and Diagnosing for the FFF Machine Based on LS-SVM
2.4. In-Situ Monitoring and Diagnosing for Product Quality Using the BPNN Model
3. Results and Discussion
3.1. The Study of Fault Diagnosis for FFF Machine
3.1.1. Signal Processing and Feature Extracted
3.1.2. Filament Jam Diagnosis Based on LS-SVM
3.2. The Study of Defects Detected for Specimens
3.2.1. Signal Processing and Feature Extracted
3.2.2. Multi-State Identification Based on BPNN
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wallin, T.J.; Pikul, J.; Shepherd, R.F. 3D printing of soft robotic systems. Nat. Rev. Mater. 2018, 3, 84–100. [Google Scholar] [CrossRef]
- Gross, B.C.; Erkal, J.L.; Lockwood, S.Y.; Chen, C.; Spence, D.M. Evaluation of 3D printing and its potential impact on biotechnology and the chemical sciences. Anal. Chem. 2014, 86, 3240–3253. [Google Scholar] [CrossRef] [PubMed]
- Quan, Z.; Wu, A.; Keefe, M.; Qin, X.; Yu, J.; Suhr, J.; Byun, J.; Kim, B.S.; Chou, T. Additive manufacturing of multidirectional preforms for composites: Opportunities and challenges. Mater. Today 2015, 18, 503–512. [Google Scholar] [CrossRef]
- BS EN ISO/ASTM 52900:2015. Additive Manufacturing—General Principles—Terminology; International Organization for Standardization: Geneva, Switzerland, 2015. [Google Scholar]
- Wang, J.; Li, H.; Liu, R.; Li, L.; Lin, Y.; Nan, C. Thermoelectric and mechanical properties of PLA/Bi0·5Sb15Te3 composite wires used for 3D printing. Compos. Sci. Technol. 2018, 157, 1–9. [Google Scholar] [CrossRef]
- Raney, J.R.; Compton, B.G.; Mueller, J.; Ober, T.J.; Shea, K.; Lewis, J.A. Rotational 3D printing of damage-tolerant composites with programmable mechanics. Proc. Natl. Acad. Sci. USA 2018, 115, 1198–1203. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Zhang, Y.; Ramanujan, D.; Ramani, K.; Chen, Y.; Williams, C.B.; Wang, C.; Shin, Y.C.; Zhang, S.; Zavattieri, P.D. The status, challenges, and future of additive manufacturing in engineering. Comput. Aided Des. 2015, 69, 65–89. [Google Scholar] [CrossRef]
- Wu, H.; Yan, W.; Yu, Z. In-situ monitoring of FDM machine condition via acoustic emission. Int. J. Adv. Manuf. Tech. 2016, 84, 1483–1495. [Google Scholar] [CrossRef]
- Wu, H.; Yu, Z.; Yan, W. Real-time FDM machine condition monitoring and diagnosis based on acoustic emission and hidden semi-Markov model. Int. J. Adv. Manuf. Tech. 2017, 90, 2027–2036. [Google Scholar] [CrossRef]
- Kim, J.S.; Lee, C.S.; Kim, S.M.; Lee, S.W. Development of data-driven in-situ monitoring and diagnosis system of fused deposition modeling (FDM) process based on support vector machine algorithm. Int. J. Precis. Eng. Manuf.-Green Technol. 2018, 5, 479–486. [Google Scholar] [CrossRef]
- Liu, J.; Hu, Y.; Wu, B.; Wang, Y. An improved fault diagnosis approach for FDM process with acoustic emission. J. Manuf. Process. 2018, 35, 570–579. [Google Scholar] [CrossRef]
- Yang, Z.; Jin, L.; Yan, Y.; Mei, Y. Filament breakage monitoring in fused deposition modeling using acoustic emission technique. Sensors 2018, 18, 749. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y. Monitoring temperature in additive manufacturing with physics-based compressive sensing. J. Manuf. Syst. 2018, 48, 60–70. [Google Scholar] [CrossRef]
- Fang, L.; Chen, T.; Li, R.; Liu, S. Application of embedded fiber bragg grating (FBG) sensors in monitoring health to 3D printing structures. IEEE Sens. J. 2016, 16, 6604–6610. [Google Scholar] [CrossRef]
- Kousiatza, C.; Karalekas, D. In-situ monitoring of strain and temperature distributions during fused deposition modeling process. Mater. Des. 2016, 97, 400–406. [Google Scholar] [CrossRef]
- Greeff, G.P.; Schilling, M. Closed loop control of slippage during filament transport in molten material extrusion. 3D Print. Addit. Manuf. 2017, 14, 31–38. [Google Scholar] [CrossRef]
- Du Plessis, A.; le Roux, S.G.; Steyn, F. Quality Investigation of 3D printer filament using laboratory X-ray tomography. Addit. Manuf. 2016, 3, 262–267. [Google Scholar] [CrossRef]
- Rao, P.K.; Liu, J.; Roberson, D.; Kong, Z.; Williams, C. Online real-time quality monitoring in additive manufacturing processes using heterogeneous sensors. J. Manuf. Sci. Eng. 2015, 137, 061007. [Google Scholar] [CrossRef]
- Sun, H.; Rao, P.K.; Kong, Z.J.; Deng, X.; Jin, R. Functional Quantitative and qualitative models for quality modeling in a fused deposition modeling process. IEEE Trans. Autom. Sci. Eng. 2018, 15, 393–403. [Google Scholar] [CrossRef]
- Soriano Heras, E.; Blaya Haro, F.; de Agustín del Burgo, J.; Islán Marcos, M.; D’Amato, R. Filament Advance Detection Sensor for Fused Deposition Modelling 3D Printers. Sensors 2018, 18, 1495. [Google Scholar] [CrossRef]
- Bell, C. 3D Printing with Delta Printers; Apress: Berkely, CA, USA, 2015. [Google Scholar]
- Fiedler, M. Evaluating Tension and Tooth Geometry to Optimize Grip on 3D Printer Filament. 3D Print. Addit. Manuf. 2015, 2, 85–88. [Google Scholar] [CrossRef]
- Volpato, N.; Kretschek, D.; Foggiatto, J.A.; Gomez da Silva Cruz, C.M. Experimental analysis of an extrusion system for additive manufacturing based on polymer pellets. Int. J. Adv. Manuf. Technol. 2015, 81, 1519–1531. [Google Scholar] [CrossRef]
- Kantaros, A.; Karalekas, D. Fiber Bragg grating based investigation of residual strains in ABS parts fabricated by fused deposition modeling process. Mater. Des. 2013, 50, 44–50. [Google Scholar] [CrossRef]
- Wang, T.; Xi, J.; Jin, Y. A model research for prototype warp deformation in the FDM process. Int. J. Adv. Manuf. Technol. 2007, 33, 1087–1096. [Google Scholar] [CrossRef]
- Hammond, O.; Li, X. In-situ real time defect detection of 3D printed parts. 3D Print. Addit. Manuf. 2017, 17, 135–142. [Google Scholar]
- Casavola, C.; Cazzato, A.; Moramarco, V.; Pappalettera, G. Residual stress measurement in Fused Deposition Modelling parts. Polym. Test. 2017, 58, 249–255. [Google Scholar] [CrossRef]
- Schimpf, V.; Max, J.B.; Stolz, B.; Heck, B.; Mülhaupt, R. Semicrystalline non-isocyanate polyhydroxyurethanes as thermoplastics and thermoplastic elastomers and their use in 3D printing by fused filament fabrication. Macromolecules 2018, 52, 320–331. [Google Scholar] [CrossRef]
- Panda, B.N.; Shankhwar, K.; Garg, A.; Jian, Z. Performance evaluation of warping characteristic of fused deposition modelling process. Int. J. Adv. Manuf. Technol. 2016, 88, 1799–1811. [Google Scholar] [CrossRef]
- Jang, Y.; Sim, J.; Park, J.; Kim, W.; Kim, H.; Kim, J. Accuracy of 3-unit fixed dental prostheses fabricated on 3D-printed casts. J. Prosthet. Dent. 2019. [Google Scholar] [CrossRef] [PubMed]
- Ertay, D.S.; Yuen, A.; Altintas, Y. Synchronized material deposition rate control with path velocity on fused deposition machines. 3D Print. Addit. Manuf. 2018, 19, 205–213. [Google Scholar]
- Anderegg, D.A.; Bryant, H.A.; Ruffin, D.C.; Skrip, S.M.; Fallon, J.J.; Gilmer, E.L.; Bortner, M.J. In-Situ Monitoring of Polymer Flow Temperature and Pressure in Extrusion Based Additive Manufacturing. 3D Print. Addit. Manuf. 2019, 26, 76–83. [Google Scholar] [CrossRef]
- Go, J.; Schiffres, S.N.; Stevens, A.G.; Hart, A.J. Rate limits of additive manufacturing by fused filament fabrication and guidelines for high-throughput system design. 3D Print. Addit. Manuf. 2017, 16, 1–11. [Google Scholar] [CrossRef]
- Li, Y.; Shi, J.; Wang, G.; Zhang, M. An ensemble model for engineered systems prognostics combining health index synthesis approach and particle filtering. Qual. Reliab. Eng. Int. 2017, 33, 2711–2725. [Google Scholar]
- Wang, L.; Gao, R. Condition monitoring and control for intelligent manufacturing. Springer Ser. Adv. Manuf. 2006, 205, 1–399. [Google Scholar]
- BS EN ISO 178:2010. Plastics—Determination of Flexural Properties; European Standards; International Organization for Standardization: Geneva, Switzerland, 2010. [Google Scholar]
- Dron, J.P.; Bolaers, F.; Rasolofondraibe, L. Improvement of the sensitivity of the scalar indicators (crest factor, kurtosis) using a de-noising method by spectral subtraction: Application to the detection of defects in ball bearings. J. Sound. Vib. 2004, 270, 61–73. [Google Scholar] [CrossRef]
- Zhang, J.; He, J.; Long, J.; Yao, M.; Zhou, W. A new denoising method for UHF PD signals using adaptive VMD and SSA-based shrinkage method. Sensors 2019, 19, 1594. [Google Scholar] [CrossRef] [PubMed]
- Chauchard, F.; Cogdill, R.; Roussel, S.; Roger, J.M.; Bellon-Maurel, V. Application of LS-SVM to non-linear phenomena in NIR spectroscopy: Development of a robust and portable sensor for acidity prediction in grapes. Chemometr. Intell. Lab. 2004, 71, 141–150. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.S. Support vector machine in machine condition monitoring and fault diagnosis. Mech. Syst. Signal. Process 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Wu, D.; He, Y.; Feng, S.; Sun, D. Study on infrared spectroscopy technique for fast measurement of protein content in milk powder based on LS-SVM. J. Food Eng. 2008, 84, 124–131. [Google Scholar] [CrossRef]
- Adankon, M.M.; Cheriet, M. Model selection for the LS-SVM. Application to handwriting recognition. Pattern Recogn. 2009, 42, 3264–3270. [Google Scholar] [CrossRef]
- Ahmad, A.S.; Hassan, M.Y.; Abdullah, M.P.; Rahman, H.A.; Hussin, F.; Abdullah, H.; Saidur, R. A review on applications of ANN and SVM for building electrical energy consumption forecasting. Renew. Sustain. Energy Rev. 2014, 33, 102–109. [Google Scholar] [CrossRef]
- Xu, X.; Vallabh, C.K.P.; Krishnan, A.; Volk, S.; Cetinkaya, C. In-process thread orientation monitoring in additive manufacturing. 3D Print. Addit. Manuf. 2019, 6, 21–23. [Google Scholar] [CrossRef]
- Charoula, K.; Nikoleta, C.; Dimitris, K. Temperature Mapping of 3D printed polymer plates: Experimental and numerical study. Sensors 2017, 17, 456. [Google Scholar]
- Heermann, P.D.; Khazenie, N. Classification of multispectral remote sensing data using a back-propagation neural network. IEEE Trans. Geosci. Remote Sens. 1992, 30, 81–88. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Sbarufatti, C.; Corbetta, M.; Giglio, M.; Cadini, F. Adaptive prognosis of lithium-ion batteries based on the combination of particle filters and radial basis function neural networks. J. Power Sources 2017, 344, 128–140. [Google Scholar] [CrossRef]
- Kuo, B.; Ho, H.; Li, C.; Huang, C.; Taur, J.S. A kernel-based feature selection method for SVM with RBF kernel for hyperspectral image classification. IEEE J.-STARS 2014, 7, 317–326. [Google Scholar]








| Type | Value |
|---|---|
| Material | Onyx |
| Extruder temperature | 265 °C |
| Nozzle diameter | 0.4 mm |
| Layer thickness | 0.2 mm |
| Filling Density | 100% |
| Filling Pattern | Rectangular |
| Filling feed rate | 40mm/s |
| Contours | 2 |
| Contour feed rate | 30 mm/s (outer), 18 mm/s (inner) |
| Working Condition | State | Cell Numbers | RMS | CF | KI | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | STD | p-Value | Mean | STD | p-Value | Mean | STD | p-Value | |||
| 45-degree filling | Normal | 50 | 0.0695 | 0.0075 | 8.13 × 10−10 | 5.61 | 1.10 | 1.06 × 10−10 | 4.03 | 1.35 | 1.06 × 10−10 |
| Filament Jam | 50 | 0.0926 | 0.0202 | 10.67 | 1.71 | 21.70 | 6.30 | ||||
| 135-degree Filling | Normal | 50 | 0.0718 | 0.007 | 2.07 × 10−9 | 5.38 | 1.02 | 1.06 × 10−10 | 3.81 | 1.16 | 1.06 × 10−10 |
| Filament Jam | 50 | 0.0914 | 0.0198 | 10.73 | 1.66 | 21.07 | 5.28 | ||||
| contour | Normal | 100 | 0.0636 | 0.0072 | 1.24 × 10−10 | 6.25 | 1.36 | 1.06 × 10−10 | 6.65 | 2.36 | 1.08 × 10−10 |
| Filament Jam | 100 | 0.0487 | 0.0091 | 8.29 | 2.17 | 11.58 | 6.65 | ||||
| Features | 45-Degree Filling | 135-Degree Filling | Contour | |||
|---|---|---|---|---|---|---|
| SVM | LS-SVM | SVM | LS-SVM | SVM | LS-SVM | |
| RMS | 80% | 82% | 80% | 81% | 81% | 81% |
| CF | 97% | 97% | 98% | 98% | 72% | 73% |
| KI | 98% | 98% | 98% | 99% | 66% | 66% |
| Odd Fill | Even Fill | Contour | |
|---|---|---|---|
| Training group | 100% | 99% | 81% |
| Testing group | 97.5% | 97.5% | 91.25% |
| Outputs | Value 1 | Value 2 | Value 3 |
|---|---|---|---|
| Normal | 1 | 0 | 0 |
| Warpage | 0 | 1 | 0 |
| Material stack | 0 | 0 | 1 |
| Channel | Normal | Warpage | Material Stack | Total | |
|---|---|---|---|---|---|
| UA | Extruder-x | 84.4% | 84% | 96.67% | 88% |
| Extruder-y | 93.33% | 68% | 93.33% | 87% | |
| Extruder-z | 95.56% | 72% | 100% | 91% | |
| Platform-z | 93.33% | 80% | 93.33% | 90% | |
| SA | 95.56% | 96% | 100% | 97% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhao, W.; Li, Q.; Wang, T.; Wang, G. In-Situ Monitoring and Diagnosing for Fused Filament Fabrication Process Based on Vibration Sensors. Sensors 2019, 19, 2589. https://doi.org/10.3390/s19112589
Li Y, Zhao W, Li Q, Wang T, Wang G. In-Situ Monitoring and Diagnosing for Fused Filament Fabrication Process Based on Vibration Sensors. Sensors. 2019; 19(11):2589. https://doi.org/10.3390/s19112589
Chicago/Turabian StyleLi, Yongxiang, Wei Zhao, Qiushi Li, Tongcai Wang, and Gong Wang. 2019. "In-Situ Monitoring and Diagnosing for Fused Filament Fabrication Process Based on Vibration Sensors" Sensors 19, no. 11: 2589. https://doi.org/10.3390/s19112589
APA StyleLi, Y., Zhao, W., Li, Q., Wang, T., & Wang, G. (2019). In-Situ Monitoring and Diagnosing for Fused Filament Fabrication Process Based on Vibration Sensors. Sensors, 19(11), 2589. https://doi.org/10.3390/s19112589






