Effect of IMU Design on IMU-Derived Stride Metrics for Running
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects and Experimental Protocol
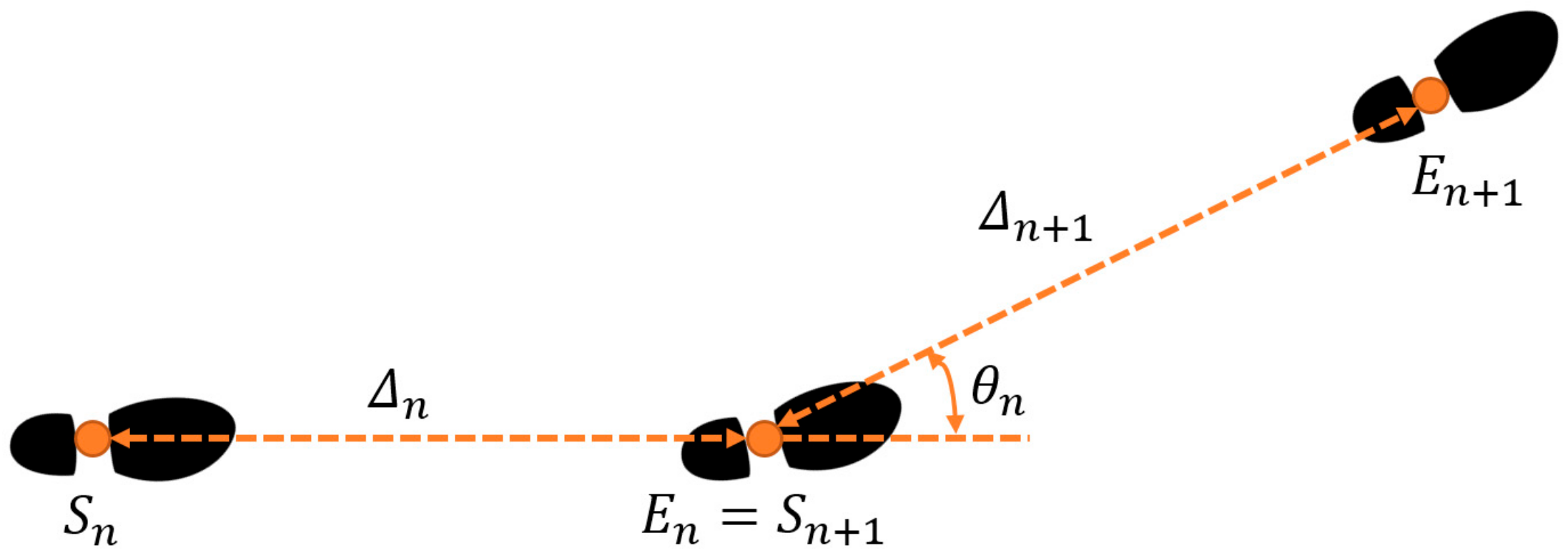
2.2. Overview of the ZUPT Method
2.3. Data Processing and Analysis
3. Results
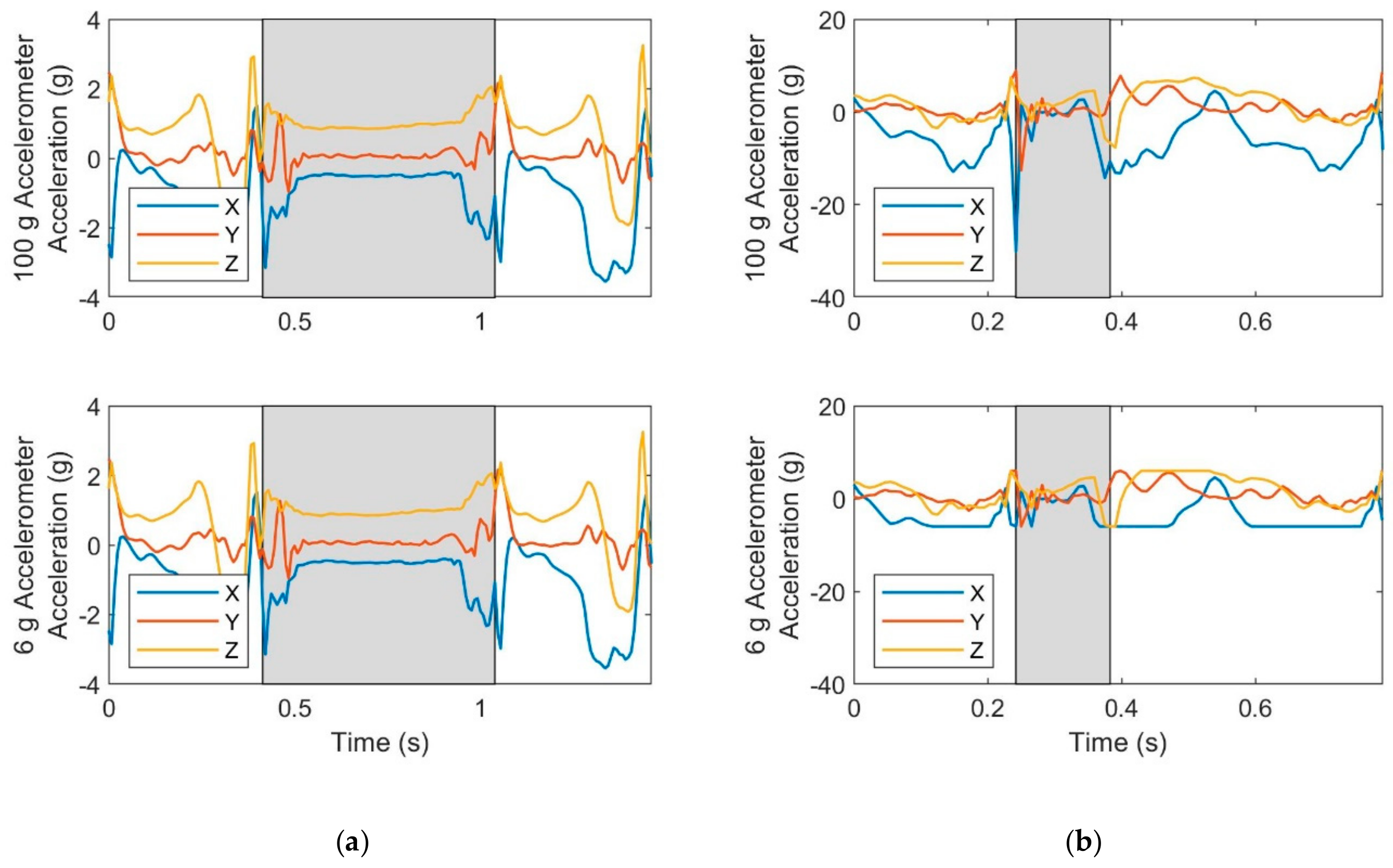
3.1. Effect of Accelerometer Range
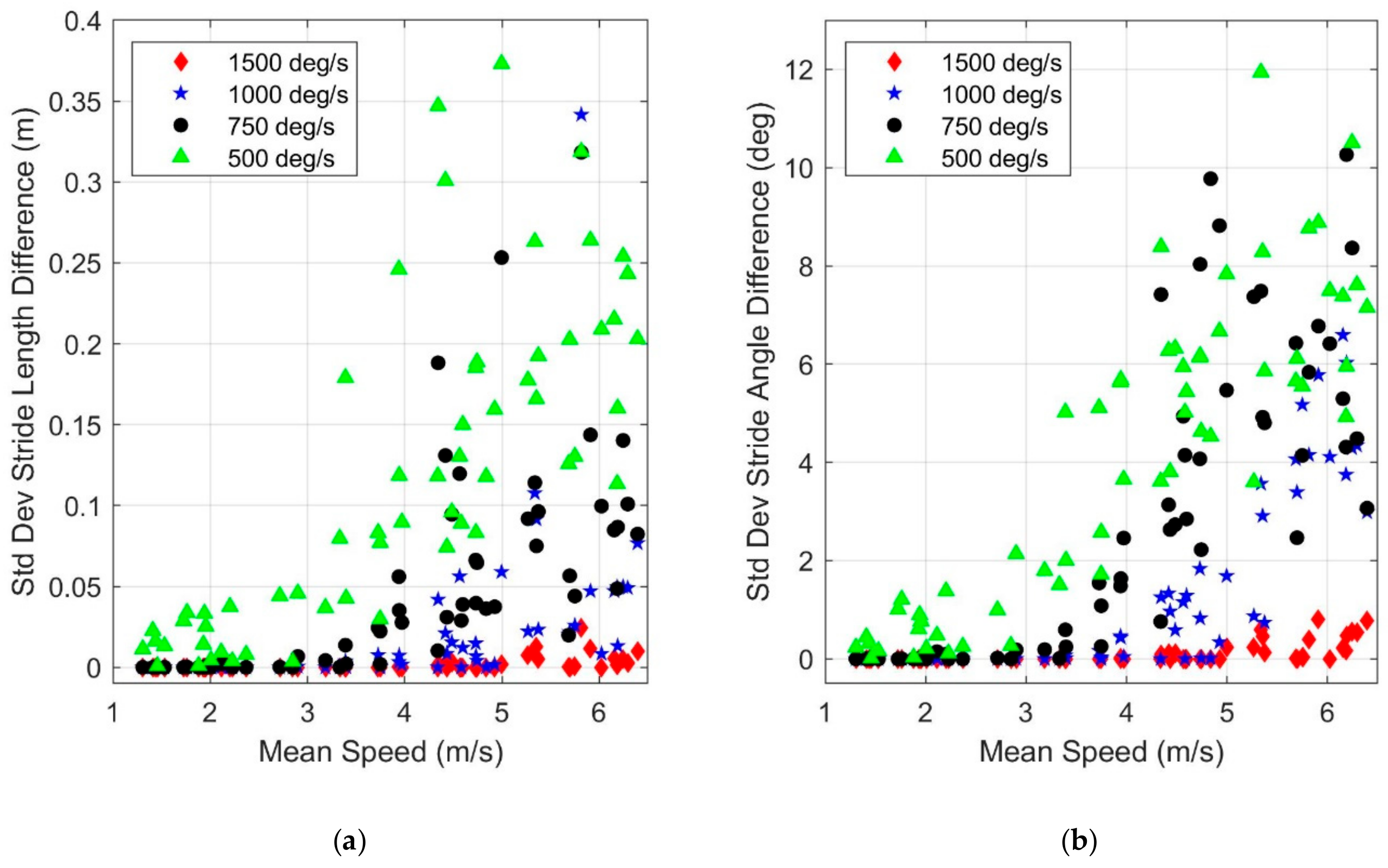
3.2. Effect of Gyro Range
3.3. Effect of Sampling Frequency
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A—Full Statistical Results from Linear Mixed-Effects Models
| Speed Effect | Estimated Slope (%/(m/s)) | p-Value | 95% Conf. Int. |
|---|---|---|---|
| Baseline (100g) | −0.39 | <0.01 | (−0.65, −0.13) |
| 75 g vs. Baseline | 0.00 | 0.99 | (−0.37, 0.37) |
| 50 g vs. Baseline | −0.03 | 0.88 | (−0.39, 0.34) |
| 24 g vs. Baseline | −0.57 | <0.01 | (−0.94, −0.21) |
| 16 g vs. Baseline | −1.08 | <0.001 | (−1.45, −0.72) |
| 10 g vs. Baseline | −2.24 | <0.001 | (−2.60, −1.87) |
| 6 g vs. Baseline | −5.70 | <0.001 | (−6.06, −5.33) |
| Speed Effect | Estimated Slope (%/(m/s)) | p-Value | 95% Conf. Int. |
|---|---|---|---|
| Baseline (2000 deg/s) | −0.41 | <0.01 | (−0.68, −0.13) |
| 1500 deg/s vs. Baseline | 0.00 | 0.99 | (−0.39, 0.39) |
| 1000 deg/s vs. Baseline | 0.05 | 0.81 | (−0.34, 0.44) |
| 750 deg/s vs. Baseline | −0.40 | <0.05 | (−0.80, −0.01) |
| 500 deg/s vs. Baseline | −3.08 | <0.001 | (−3.47, −2.69) |
| Speed Effect | Estimated Slope (%/(m/s)) | p-Value | 95% Conf. Int. |
|---|---|---|---|
| Baseline (1000 Hz) | −1.12 | <0.001 | (−1.48, −0.77) |
| 500 Hz vs. Baseline | −0.09 | 0.73 | (−0.59, 0.41) |
| 250 Hz vs. Baseline | −0.13 | 0.63 | (−0.63, 0.38) |
| 125 Hz vs. Baseline | −0.26 | 0.32 | (−0.76, 0.24) |
| 62.5 Hz vs. Baseline | 0.94 | <0.001 | (0.44, 1.44) |
| Speed Effect | Estimated Slope (%/(m/s)) | p-Value | 95% Conf. Int. |
|---|---|---|---|
| Baseline (1000 Hz) | −1.17 | <0.001 | (−1.50, −0.85) |
| 500 Hz vs. Baseline | −0.01 | 0.96 | (−0.47, 0.45) |
| 250 Hz vs. Baseline | −0.03 | 0.90 | (−0.49, 0.43) |
| 125 Hz vs. Baseline | 0.08 | 0.74 | (−0.38, 0.54) |
| 62.5 Hz vs. Baseline | 0.12 | 0.60 | (−0.33, 0.58) |
References
- Cavanagh, P.R.; Kram, R. Stride length in distance running: Velocity, body dimensions, and added mass effects. Med. Sci. Sports Exerc. 1989, 21, 467–479. [Google Scholar] [CrossRef] [PubMed]
- Novacheck, T.F. The biomechanics of running. Gait Posture 1998, 7, 77–95. [Google Scholar] [CrossRef]
- Norris, M.; Anderson, R.; Kenny, I.C. Method analysis of accelerometers and gyroscopes in running gait: A systematic review. Proc. Inst. Mech. Eng. Part P J. Sport Eng. Technol. 2014, 228, 3–15. [Google Scholar] [CrossRef]
- Ojeda, L.V.; Borenstein, J. Non-GPS navigation for security personnel and first responders. J. Navig. 2007, 60, 391–407. [Google Scholar] [CrossRef]
- Foxlin, E. Pedestrian tracking with shoe-mounted inertial sensors. IEEE Comput. Graph. Appl. 2005, 25, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Reenalda, J.; Maartens, E.; Homan, L.; Buurke, J.H.J. Continuous three dimensional analysis of running mechanics during a marathon by means of inertial magnetic measurement units to objectify changes in running mechanics. J. Biomech. 2016, 49, 3362–3367. [Google Scholar] [CrossRef] [PubMed]
- Xing, H.; Li, J.; Hou, B.; Zhang, Y.; Guo, M. Pedestrian stride length estimation from IMU measurements and ANN based algorithm. J. Sens. 2017. [Google Scholar] [CrossRef]
- Hollman, J.H.; Watkins, M.K.; Imhoff, A.C.; Braun, C.E.; Akervik, K.A.; Ness, D.K. A comparison of variability in spatiotemporal gait parameters between treadmill and overground walking conditions. Gait Posture 2016, 43, 204–209. [Google Scholar] [CrossRef]
- Rebula, J.R.; Ojeda, L.V.; Adamczyk, P.G.; Kuo, A.D. Measurement of foot placement and its variability with inertial sensors. Gait Posture 2013, 38, 974–980. [Google Scholar] [CrossRef] [Green Version]
- Sabatini, A.M.; Martelloni, C.; Scapellato, S.; Cavallo, F. Assessment of walking features from foot inertial sensing. IEEE Trans. Biomed. Eng. 2005, 52, 486–494. [Google Scholar] [CrossRef]
- Elwell, J. Inertial navigation for the urban warrior. In Proceedings of the SPIE; SPIE: Bellingham, WA, USA, 1999; Volume 3709, pp. 196–204. [Google Scholar]
- Ojeda, L.V.; Rebula, J.R.; Adamczyk, P.G.; Kuo, A.D. Mobile platform for motion capture of locomotion over long distances. J. Biomech. 2013, 46, 2316–2319. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kitagawa, N.; Ogihara, N. Estimation of foot trajectory during human walking by a wearable inertial measurement unit mounted to the foot. Gait Posture 2016, 45, 110–114. [Google Scholar] [CrossRef] [PubMed]
- Brahms, C.M.; Zhao, Y.; Gerhard, D.; Barden, J.M. Stride length determination during overground running using a single foot-mounted inertial measurement unit. J. Biomech. 2018, 71, 302–305. [Google Scholar] [CrossRef] [PubMed]
- Leskinen, A.; Häkkinen, K.; Virmavirta, M.; Isolehto, J.; Kyröläinen, H. Comparison of running kinematics between elite and national-standard 1500-m runners. Sports Biomech. 2009, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Hanley, B. Pacing, packing and sex-based differences in Olympic and IAAF World Championship marathons. J. Sports Sci. 2016, 34, 1675–1681. [Google Scholar] [CrossRef] [PubMed]
- Hoogkamer, W.; Kram, R.; Arellano, C.J. How Biomechanical Improvements in Running Economy Could Break the 2-h Marathon Barrier. Sports Med. 2017, 47, 1739–1750. [Google Scholar] [CrossRef] [PubMed]
- Peruzzi, A.; Della Croce, U.; Cereatti, A. Estimation of stride length in level walking using an inertial measurement unit attached to the foot: A validation of the zero velocity assumption during stance. J. Biomech. 2011, 44, 1991–1994. [Google Scholar] [CrossRef]
- Bailey, G.P.; Harle, R.K. Investigation of sensor parameters for kinematic assessment of steady state running using foot mounted IMUs. In Proceedings of the 2nd International Congress on Sports Sciences Research and Technology Support, Rome, Italy, 16–18 October 2014; pp. 154–161. [Google Scholar]
- Ojeda, L.V.; Rebula, J.R.; Kuo, A.D.; Adamczyk, P.G. Influence of contextual task constraints on preferred stride parameters and their variabilities during human walking. Med. Eng. Phys. 2015, 37, 929–936. [Google Scholar] [CrossRef] [Green Version]
- Potter, M.V.; Ojeda, L.V.; Perkins, N.C.; Cain, S.M. Influence of accelerometer range on accuracy of foot-mounted IMU based running velocity estimation. In Proceedings of the Annual Meeting of the American Society of Biomechanics, Boulder, CO, USA, 8–11 August 2017; pp. 1133–1134. [Google Scholar]
- Mitschke, C.; Kiesewetter, P.; Milani, T.L. The effect of the accelerometer operating range on biomechanical parameters: Stride length, velocity, and peak tibial acceleration during running. Sensors 2018, 18. [Google Scholar] [CrossRef]
- Ojeda, L.V.; Zaferiou, A.M.; Cain, S.M.; Vitali, R.V.; Davidson, S.P.; Stirling, L.A.; Perkins, N.C. Estimating stair running performance using inertial sensors. Sensors 2017, 17. [Google Scholar] [CrossRef]
- Bailey, G.P.; Harle, R. Assessment of foot kinematics during steady state running using a foot-mounted IMU. Procedia Eng. 2014, 72, 32–37. [Google Scholar] [CrossRef]
- Bates, D.; Maechler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Nyquist, H. Certain topics in telegraph transmission theory. Trans. AIEE 1928, 47, 617–644. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication in the presence of noise. Proc. Inst. Radio Eng. 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Antoniou, A. Digital Signal. Processing; McGraw-Hill Education: New York, NY, USA, 2006; ISBN 0-07-145424-1. [Google Scholar]
- Lyons, R. Understanding Digital Signal. Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2001; ISBN 0-201-63467-8. [Google Scholar]
- MATLAB Decimate. Available online: https://www.mathworks.com/help/signal/ref/decimate.html (accessed on 25 July 2018).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: https://www.R-project.org (accessed on 7 March 2019).
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest Package: Tests in Linear Mixed Effects Models. J. Stat. Softw. 2017, 82, 1–26. [Google Scholar] [CrossRef] [Green Version]









| IMU 1 | IMU 2 | |
|---|---|---|
| Model | Opal | Custom design |
| Manufacturer | APDM | Insight Sports, Ltd. |
| Sampling Frequency (Hz) | 128 | 1000 |
| Accelerometer Range (g) | ±200 | ±32 |
| Angular Gyro Range (deg/s) | ±2000 | ±4000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Potter, M.V.; Ojeda, L.V.; Perkins, N.C.; Cain, S.M. Effect of IMU Design on IMU-Derived Stride Metrics for Running. Sensors 2019, 19, 2601. https://doi.org/10.3390/s19112601
Potter MV, Ojeda LV, Perkins NC, Cain SM. Effect of IMU Design on IMU-Derived Stride Metrics for Running. Sensors. 2019; 19(11):2601. https://doi.org/10.3390/s19112601
Chicago/Turabian StylePotter, Michael V, Lauro V Ojeda, Noel C Perkins, and Stephen M Cain. 2019. "Effect of IMU Design on IMU-Derived Stride Metrics for Running" Sensors 19, no. 11: 2601. https://doi.org/10.3390/s19112601
APA StylePotter, M. V., Ojeda, L. V., Perkins, N. C., & Cain, S. M. (2019). Effect of IMU Design on IMU-Derived Stride Metrics for Running. Sensors, 19(11), 2601. https://doi.org/10.3390/s19112601






