A Differential Pressure Sensor Coupled with Conductance Sensors to Evaluate Pressure Drop Prediction Models of Gas-Water Two-Phase Flow in a Vertical Small Pipe
Abstract
:1. Introduction
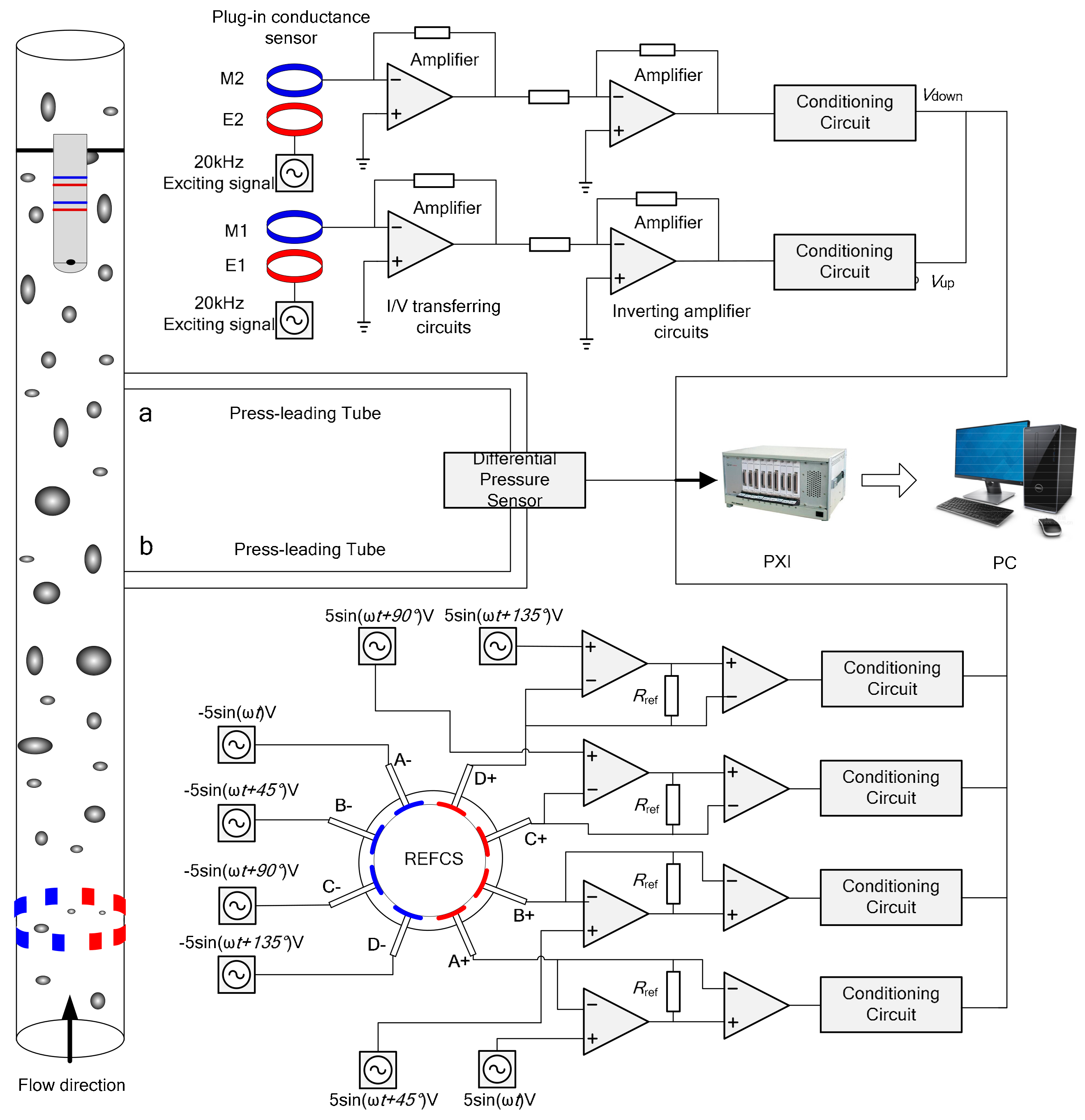
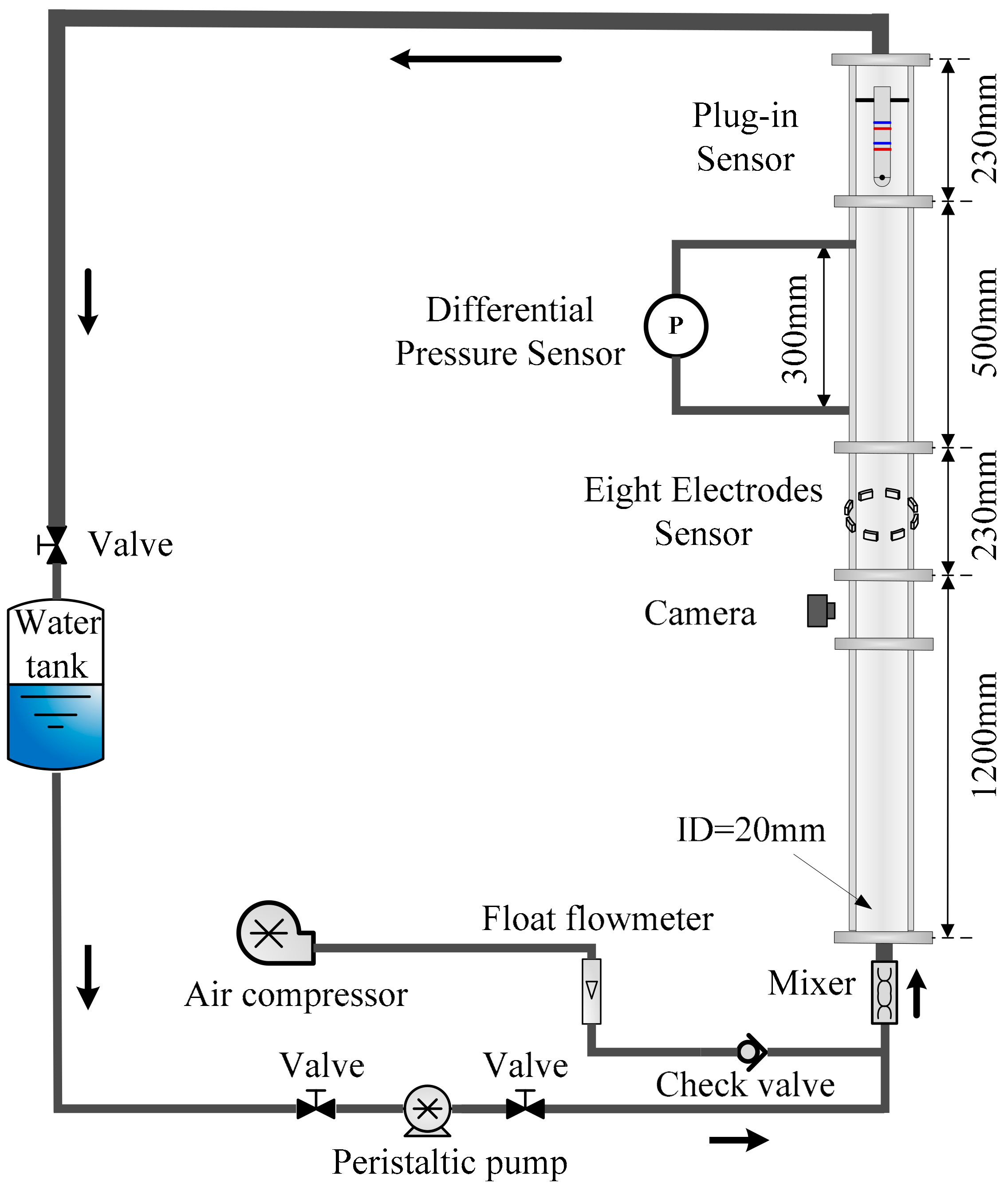
2. Measurement System and Experiment Setup
2.1. Measurement System
2.2. Experimental Facility
3. Prediction Models of Pressure Drop
3.1. Asheim Model
3.2. Hasan-Kabir Model
3.3. Ansari et al. Model
3.4. Zhang et al. Model
3.5. Dynamic Two-Fluid Model
4. Results and Discussion
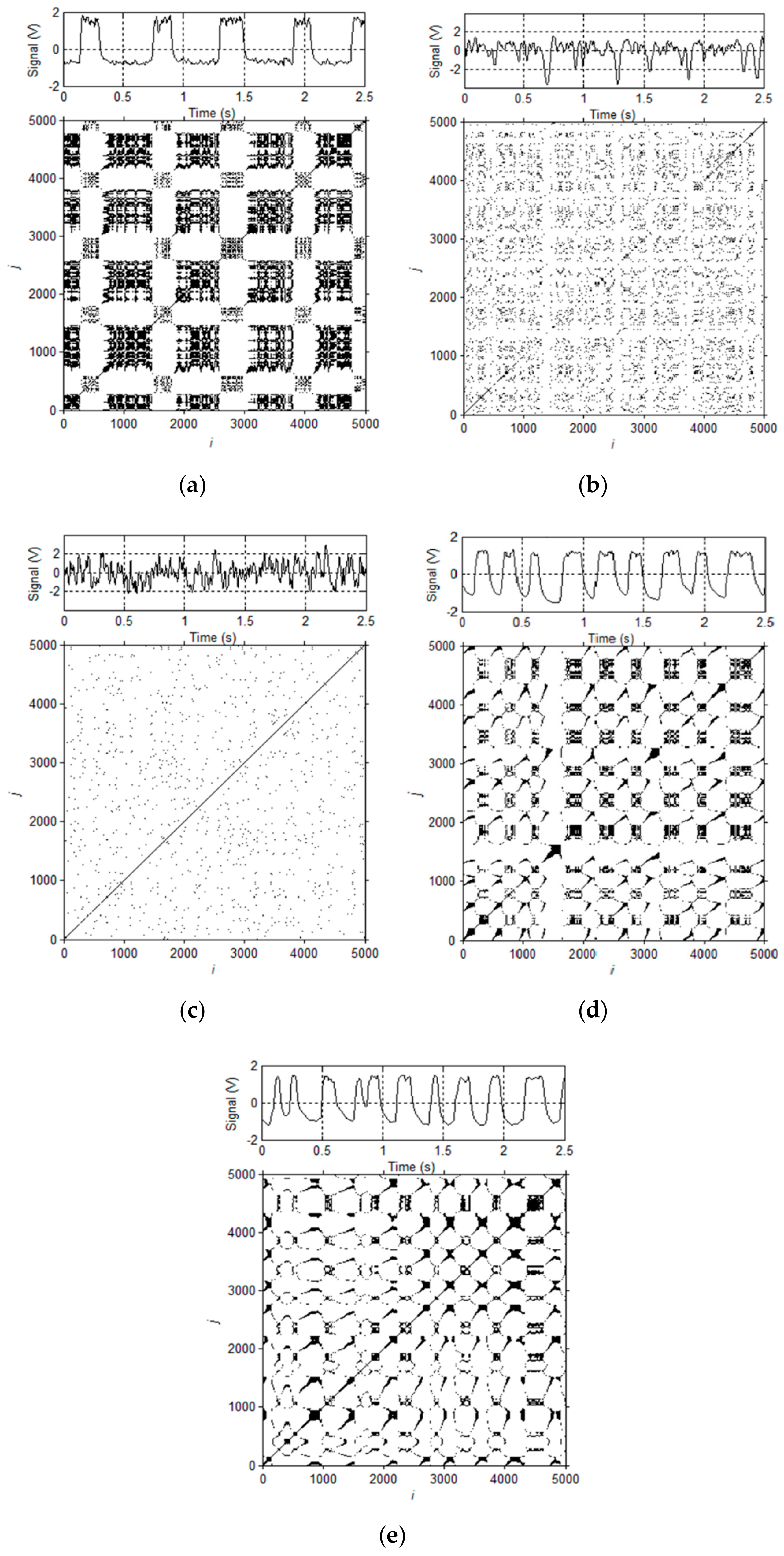
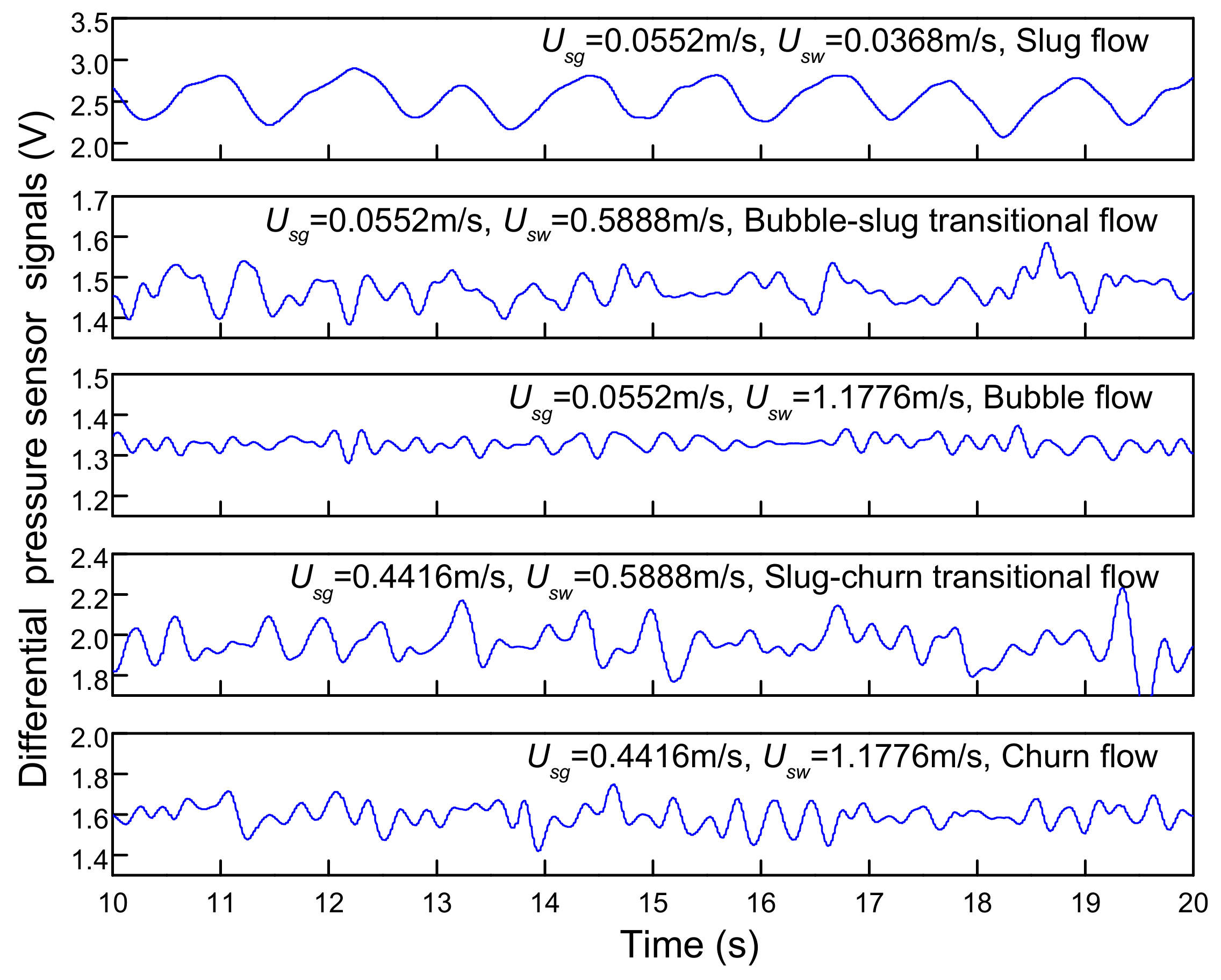
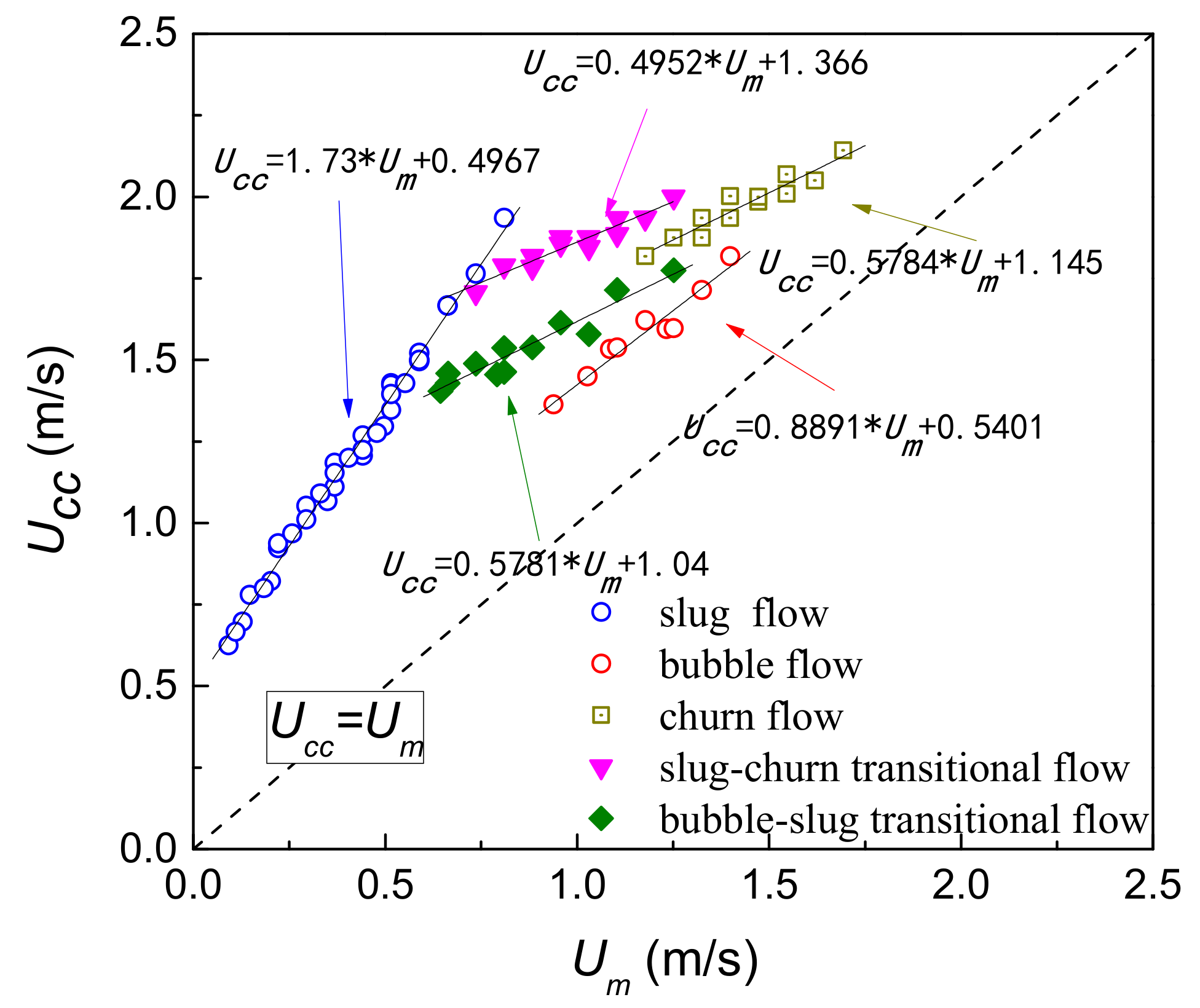
4.1. Flow Pattern Identification
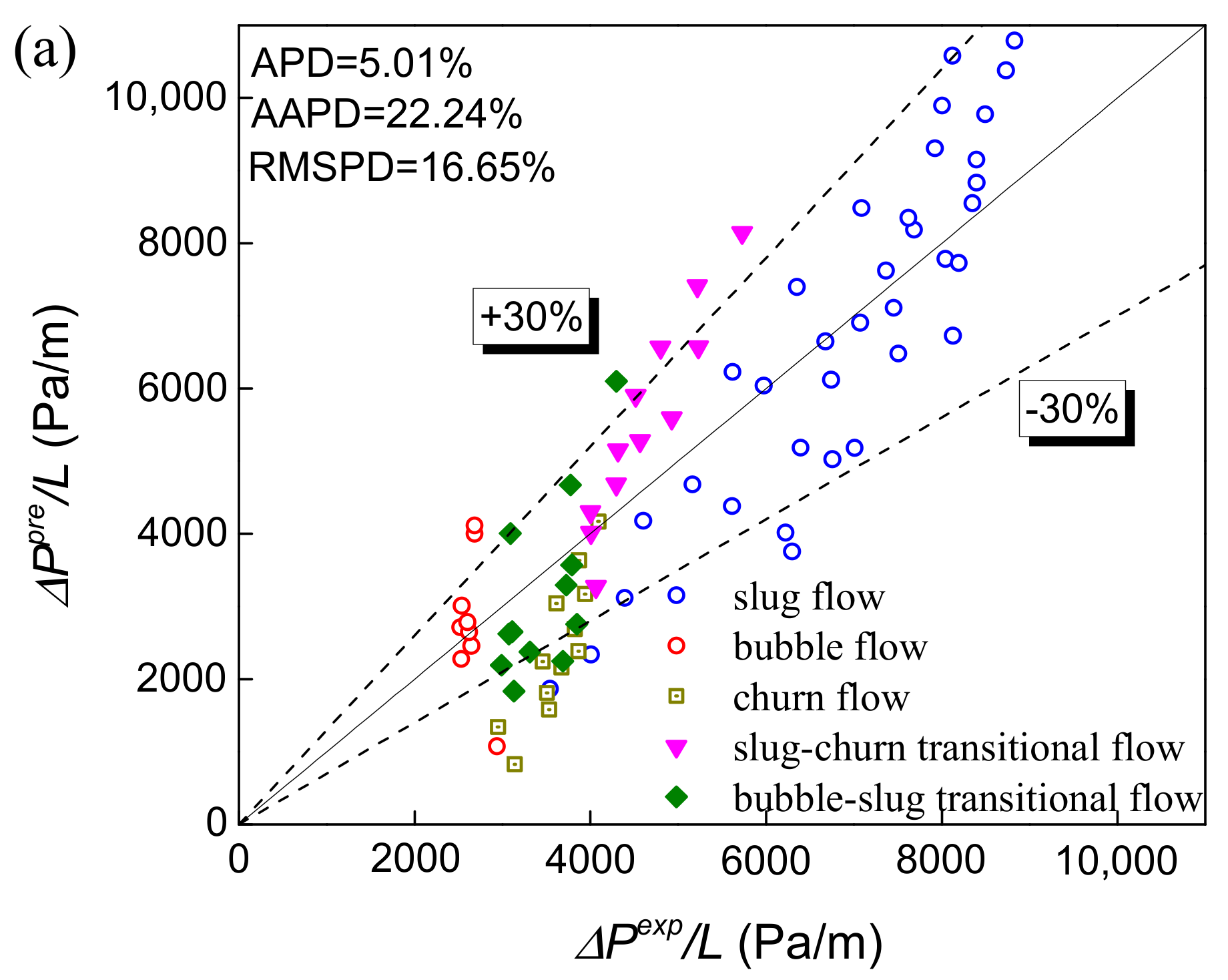
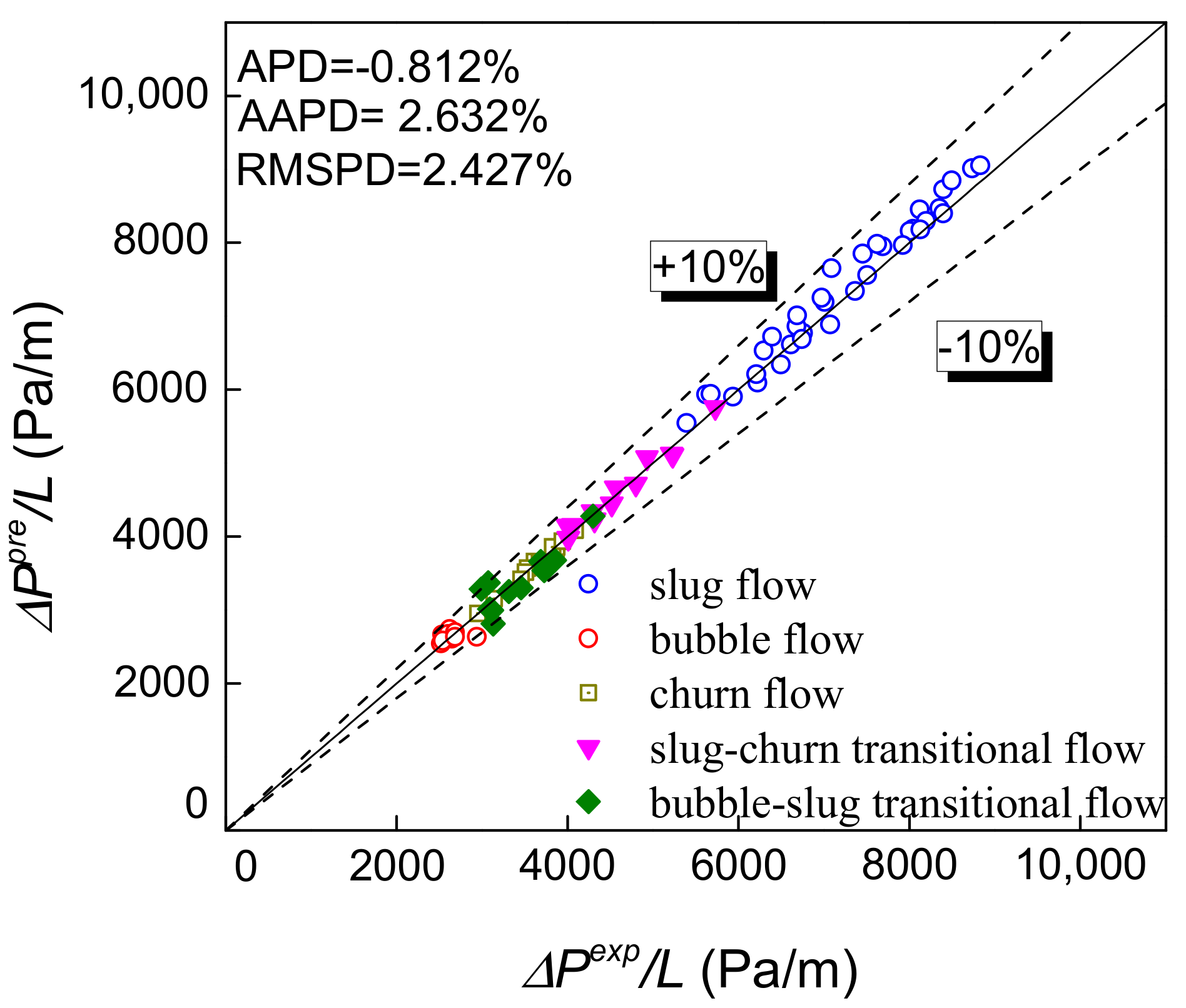
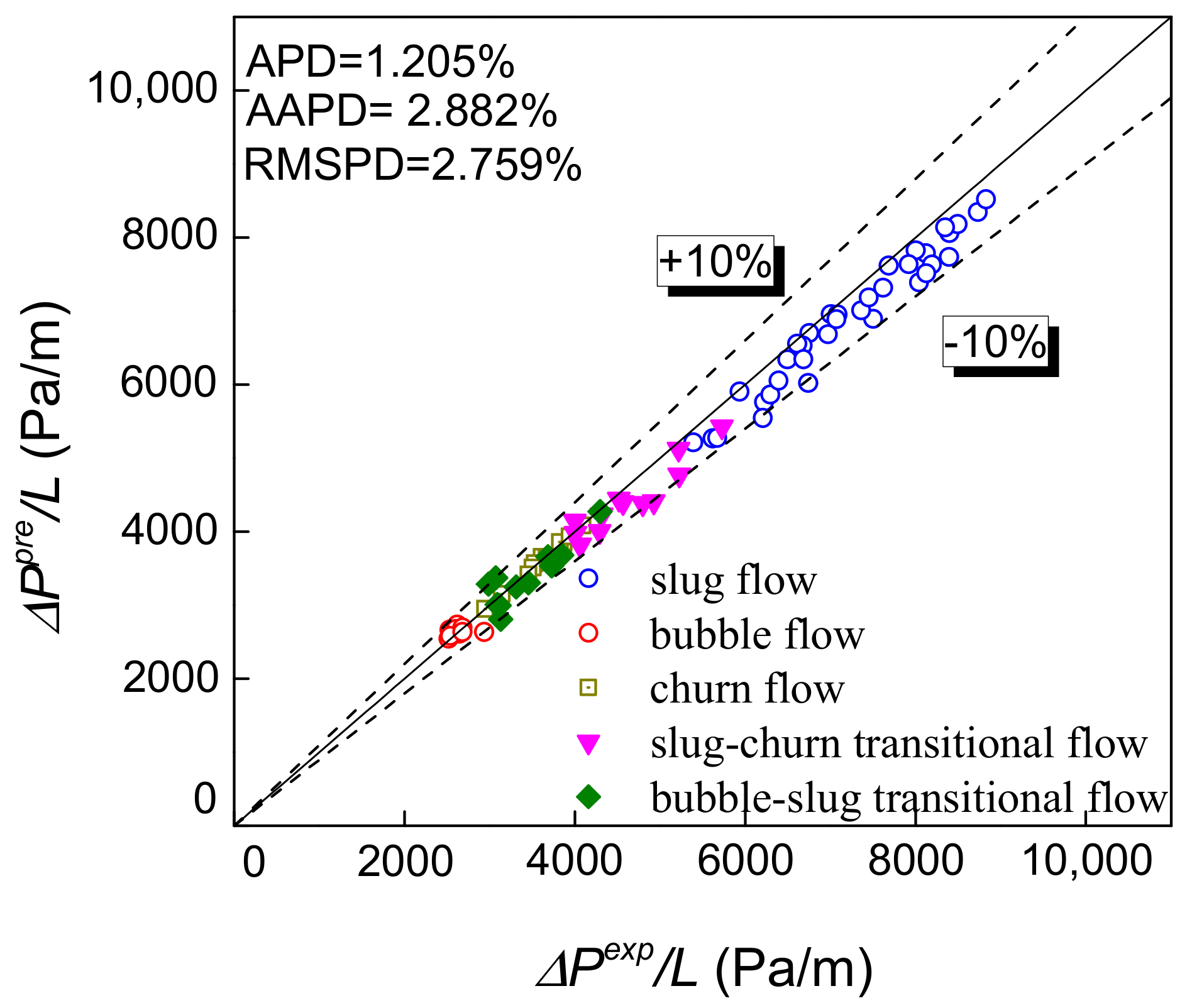
4.2. Model Test
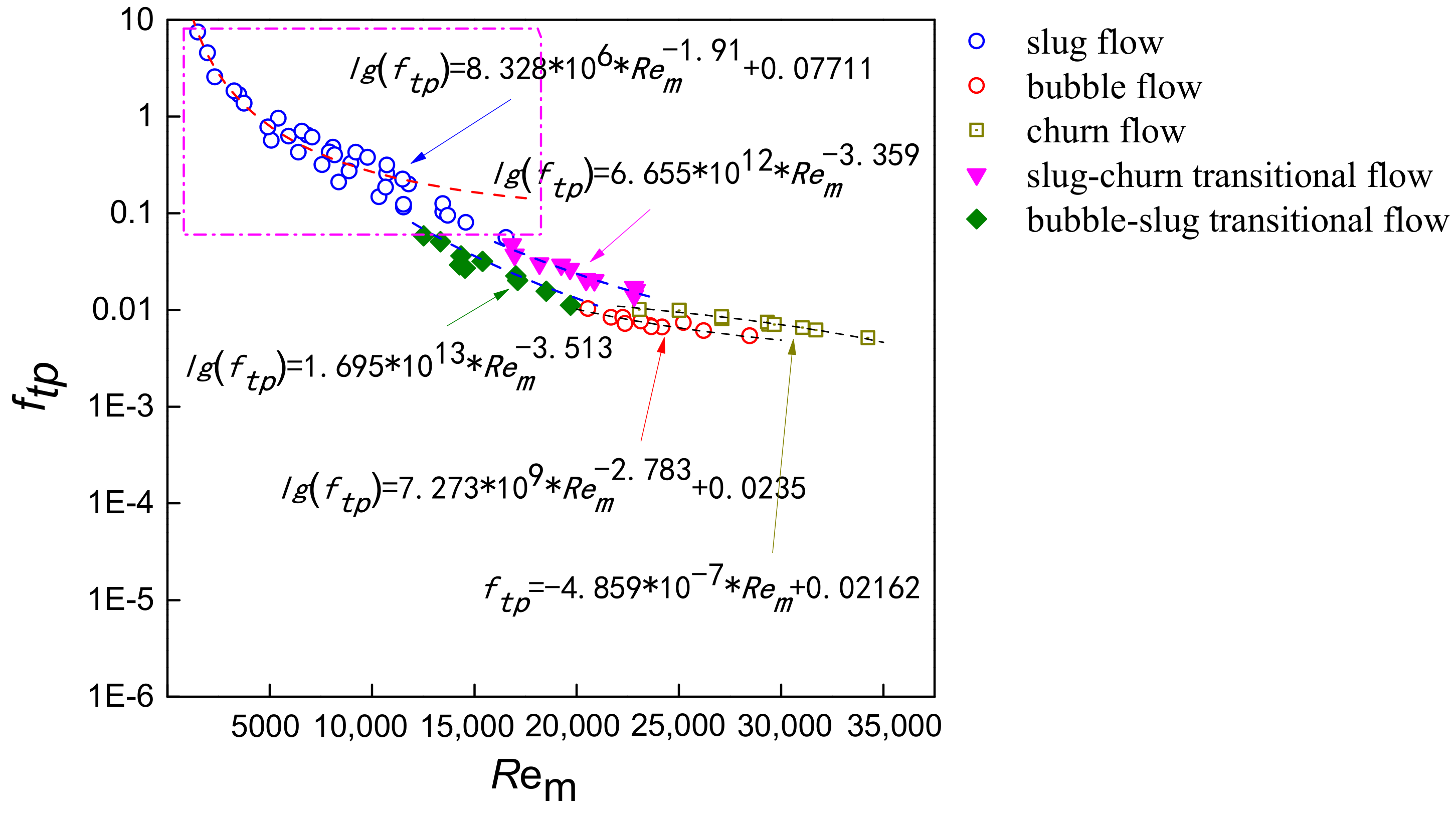
5. Pressure Drop Prediction
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| d | pipe diameter |
| f | friction factor |
| g | acceleration due to gravity |
| H | average holdup fraction |
| L | length along the pipe |
| v | velocity |
| β | length ratio |
| ϴ | angle from horizontal |
| λ | no-slip gas holdup fraction |
| ρ | density |
| Γ | interaction force |
| σ | surface tension |
| Subscripts | |
| e | elevation |
| f | film |
| g | gas |
| i | x direction |
| L | liquid |
| LS | liquid slug |
| r | relative |
| s | shear stress |
| SU | slug unit |
| tp | two-phase |
| TB | taylor bubble |
| w | wall |
References
- Zhai, L.S.; Bian, P.; Han, Y.F.; Jin, N.D. The measurement of gas–liquid two-phase flows in a small diameter pipe using a dual-sensor multi-electrode conductance probe. Meas. Sci. Technol. 2016, 27, 045101. [Google Scholar] [CrossRef]
- Gao, Z.K.; Yang, Y.; Zhai, L.S.; Jin, N.D.; Chen, G. A four-sector conductance method for measuring and characterizing low-velocity oil-water two-phase flows. IEEE Trans. Instrum. Meas. 2016, 65, 1690–1697. [Google Scholar] [CrossRef]
- Merilo, M.; Dechene, R.L.; Cichowlas, W.M. Void fraction measurement with rotating electric field conductance gauge. J. Heat Trans. 1977, 99, 2. [Google Scholar] [CrossRef]
- Rocha, M.S.; Simões-Moreira, J.R. Void fraction measurement and signal analysis from multiple-electrode impedance sensors. Heat Transf. Eng. 2008, 29, 12. [Google Scholar] [CrossRef]
- Zhuang, L.X.; Jin, N.D.; Zhao, A.; Gao, Z.K.; Zhai, L.S.; Tang, Y. Nonlinear multi-scale dynamic stability of oil–gas–water three-phase flow in vertical upward pipe. Chem. Eng. J. 2016, 302, 595–608. [Google Scholar] [CrossRef]
- Beck, M.S. Correlation in instruments: Cross correlation flowmeters. J. Phys. E Sci. Instrum. 1981, 14, 7–19. [Google Scholar] [CrossRef]
- Yan, Y. Mass flow measurement of bulk solids in pneumatic pipelines. Meas. Sci. Technol. 1996, 7, 1687–1706. [Google Scholar] [CrossRef]
- Takashima, S.; Asanuma, H.; Niitsuma, H. A water flowmeter using dual fiber Bragg grating sensors and cross-correlation technique. Sens. Actuators A Phys. 2004, 116, 66–74. [Google Scholar] [CrossRef]
- Saoud, A.; Mosorov, V.; Grudzien, K. Measurement of velocity of gas/solid swirl flow using Electrical Capacitance Tomography and cross correlation technique. Flow Meas. Instrum. 2016, 53, 133–140. [Google Scholar] [CrossRef]
- Jin, H.; Han, Y.; Yang, S.; He, G. Electrical resistance tomography coupled with differential pressure measurement to determine phase hold-ups in gas–liquid–solid outer loop bubble column. Flow Meas. Instrum. 2010, 21, 228–232. [Google Scholar] [CrossRef]
- Shafquet, A.; Ismail, I. Measurement of void fraction by using electrical capacitance sensor and differential pressure in air-water bubble flow. In Proceedings of the 2012 4th International Conference on Intelligent and Advanced Systems, Kuala Lumpur, Malaysia, 12–14 June 2012. [Google Scholar]
- Jia, J.; Babatunde, A.; Wang, M. Void fraction measurement of gas–liquid two-phase flow from differential pressure. Flow Meas. Instrum. 2015, 41, 75–80. [Google Scholar] [CrossRef]
- Lockhart, R.W.; Martinelli, R.C. Proposed correlation of data for isothermal two-phase, two-component flow in pipes. Chem. Eng. Prog. 1949, 45, 39–48. [Google Scholar]
- Fancher, J.R.; Brown, K.E. Prediction of pressure gradients for multiphase flow in tubing. SPE 1963, 3, 59–69. [Google Scholar] [CrossRef]
- Chisholm, D. Pressure gradients due to friction during the flow of evaporating two-phase mixtures in smooth tubes and channels. Int. J. Heat Mass Transf. 1973, 16, 347–358. [Google Scholar] [CrossRef]
- Müller-Steinhagen, H.; Heck, K. A simple friction pressure drop correlation for two-phase flow in pipes. Chem. Eng. Process. 1986, 20, 297–308. [Google Scholar] [CrossRef]
- Poettman, F.H.; Carpenter, P.G. The multiphase flow of gas, oil, and water through vertical flow strings with application to the design of gas-lift installations. In Drilling and Production Practice; American Petroleum Institute: New York, NY, USA, 1952; p. 257. [Google Scholar]
- Baxendell, P.B.; Thomas, R. The calculation of pressure gradients in high-rate flowing wells. J. Petrol. Technol. 1961, 13, 1023–1028. [Google Scholar] [CrossRef]
- Hagedorn, A.R.; Brown, K.E. Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits. J. Petrol. Technol. 1965, 17, 475–484. [Google Scholar] [CrossRef]
- Duns, J.H.; Ros, D.J. Vertical flow of gas and liquid mixtures in wells. In Proceedings of the 6th World Petroleum Congress, Frankfurt am Main, Germany, 19–26 June 1963. [Google Scholar]
- Chierici, G.L.; Ciucci, G.M.; Sclocchi, G. Two-phase vertical flow in oil wells—Prediction of pressure drop. J. Petrol. Technol. 1974, 26, 927–938. [Google Scholar] [CrossRef]
- Asheim, H. An accurate two-phase well flow model based on phase slippage. SPE Prod. Eng. 1986, 1, 221–230. [Google Scholar] [CrossRef]
- Sarica, C.; Schmidt, Z.; Doty, D. A Mechanistic Model for Predicting Pressure Drop in Vertical Upward Two-Phase Flow. J. Energ. Resour. ASME 1999, 121, 1–8. [Google Scholar]
- Abdul-Majeed, G.H.; Al-Mashat, A.M. A mechanistic model for vertical and inclined two-phase slug flow. J. Petrol. Sci. Eng. 2000, 27, 59–67. [Google Scholar] [CrossRef]
- Shiferaw, D.; Mahmoud, M.; Karayiannis, T.G.; Kenning, D.B.R. One-dimensional semi mechanistic model for flow boiling pressure drop in small to micro passages. Heat Transf. Eng. 2011, 32, 1150–1159. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. Performance of a two-phase gas/liquid flow model in vertical wells. J. Petrol. Sci. Eng. 1990, 4, 273–289. [Google Scholar]
- Ansari, A.M.; Sylvester, N.D.; Sarica, C.; Shoham, O. A comprehensive mechanistic model for upward two-phase flow. SPE Prod. Facil. 1994, 9, 143–151. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Jayawardena, S.S.; Redus, C.L.; Brill, J.P. Slug Dynamics in Gas-Liquid Pipe Flow. J. Energ. Resour. ASME 2000, 122, 14–21. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Wang, Q.; Sarica, C.; Brill, J.P. A unified mechanistic model for slug liquid holdup and transition between slug and dispersed bubble flows. Int. J. Multiph. Flow 2003, 29, 97–107. [Google Scholar] [CrossRef]
- Yan, K.; Che, D. Hydrodynamic and mass transfer characteristics of slug flow in a vertical pipe with and without dispersed small bubbles. Int. J. Multiph. Flow 2011, 37, 299–325. [Google Scholar] [CrossRef]
- Abdulkadir, M.; Hernandez-Perez, V.; Lowndes, I.S.; Azzopardi, B.J.; Dzomeku, S. Experimental study of the hydrodynamic behaviour of slug flow in a vertical riser. Chem. Eng. Sci. 2014, 106, 60–75. [Google Scholar] [CrossRef]
- Wang, D.Y.; Jin, N.D.; Zhuang, L.X.; Zhai, L.S.; Ren, Y.Y. Development of a rotating electric field conductance sensor for measurement of water holdup in vertical oil–gas–water flows. Meas. Sci. Technol. 2018, 29, 075301. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Oxford: Clarendon, UK, 1882. [Google Scholar]
- Moody, L.F. Friction factors for pipe flow. J. Appl. Mech. Trans. ASME 1944, 66, 671–684. [Google Scholar]
- Harmathy, T.Z. Velocity of large drops and bubbles in media of infinite or restricted extent. AIChE J. 2010, 6, 281–288. [Google Scholar] [CrossRef]
- Wallis, G.B. Minimum critical velocity for one-phase flow of liquids, Industrial and Engineering Chemistry Process Design and Development. Ind. Eng. Chem. Res. 1970, 9, 486. [Google Scholar]
- Zuber, N.; Hench, J. Steady State and Transient Void Fraction of Bubbling Systems and Their Operating Limit; Part I: Steady State Operation; General Electric Report 62GL100; General Electric: Boston, MA, USA, 1962. [Google Scholar]
- Jin, N.D.; Zheng, G.B.; Chen, W.P. Chaotic recurrence characteristics analysis of conductance fluctuating signal of gas/liquid two-phase flow. J. Chem. Ind. Eng. 2007, 58, 1172–1179. [Google Scholar]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.-R.; Jin, N.-D.; Yang, Q.-Y.; Wang, D.-Y. A Differential Pressure Sensor Coupled with Conductance Sensors to Evaluate Pressure Drop Prediction Models of Gas-Water Two-Phase Flow in a Vertical Small Pipe. Sensors 2019, 19, 2723. https://doi.org/10.3390/s19122723
Deng Y-R, Jin N-D, Yang Q-Y, Wang D-Y. A Differential Pressure Sensor Coupled with Conductance Sensors to Evaluate Pressure Drop Prediction Models of Gas-Water Two-Phase Flow in a Vertical Small Pipe. Sensors. 2019; 19(12):2723. https://doi.org/10.3390/s19122723
Chicago/Turabian StyleDeng, Yuan-Rong, Ning-De Jin, Qiu-Yi Yang, and Da-Yang Wang. 2019. "A Differential Pressure Sensor Coupled with Conductance Sensors to Evaluate Pressure Drop Prediction Models of Gas-Water Two-Phase Flow in a Vertical Small Pipe" Sensors 19, no. 12: 2723. https://doi.org/10.3390/s19122723



