Azimuth Sidelobes Suppression Using Multi-Azimuth Angle Synthetic Aperture Radar Images
Abstract
:1. Introduction
2. Multi-Pass Squinted SAR
3. Signal Processing
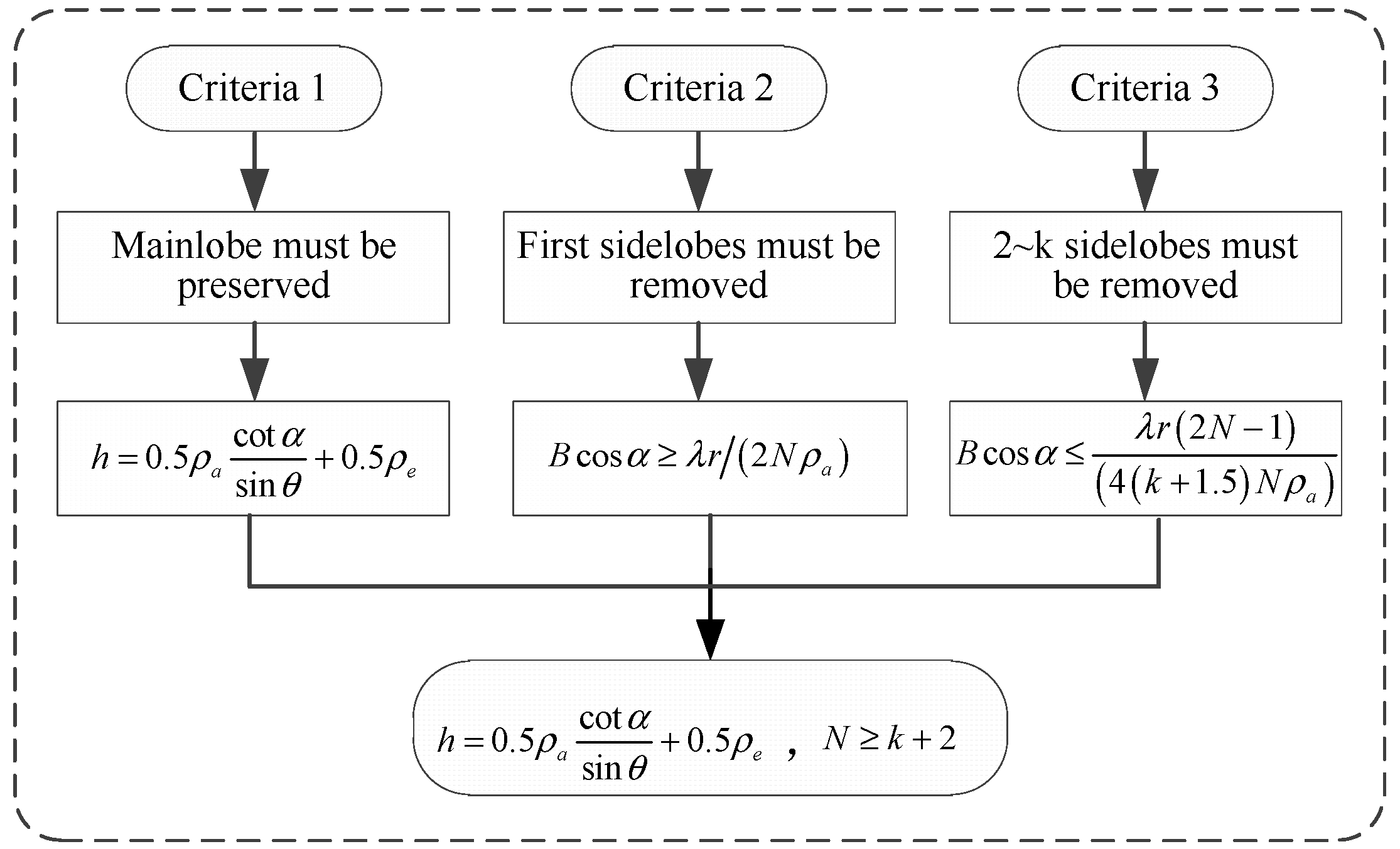
4. Parameter Design
4.1. The Energy of the Azimuth Mainlobe Must be Preserved
4.2. The First Azimuth Sidelobes in Elevation Must Be Outside the Integrating Range
4.3. The 2nd to the Kth Azimuth Sidelobes in Elevation Must Be Outside the Integrating Range
5. Performance Simulation
5.1. Point Target Simulations
5.2. Real SAR Image Simulations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Prabhu, K.M.M. Window Functions and Their Applications in Signal Processing; CRC Press: Boca Raton, FL, USA, July 2014. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Cohen, I.; Levanon, N. Weight Windows—An Improved Approach. In Proceedings of the 2014 IEEE 28th Convention of Electrical & Electronics Engineers in Israel (IEEEI), Eilat, Israel, 3–5 December 2014. [Google Scholar]
- Stankwitz, H.C.; Dallaire, R.J.; Fienup, J.R. Spatially variant apodization for sidelobe control in SAR imagery. In Proceedings of the 1994 IEEE National Radar Conference, Atlanta, GA, USA, 29–31 March 1994; pp. 132–137. [Google Scholar]
- Stankwitz, H.C.; Dallaire, R.J.; Fienup, J.R. Nonlinear apodization for sidelobe control in SAR imagery. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 267–279. [Google Scholar] [CrossRef]
- Smith, B.H. Generalization of spatially variant apodization to noninteger Nyquist sampling rates. IEEE Trans. Image Process. 2000, 9, 1088–1093. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Rubio, C.F.; Llorente-Romano, S.; Burgos-Garcia, M. Spatially variant apodization for squinted synthetic aperture radar images. IEEE Trans. Image Process. 2007, 16, 2023–2027. [Google Scholar] [CrossRef] [PubMed]
- Iglesias, R.; Mallorqui, J.J. Side-lobe cancelation in DInSAR pixel selection with SVA. IEEE Geosci. Remote Sens. Lett. 2013, 10, 667–671. [Google Scholar] [CrossRef]
- Xiong, T.; Wang, S.; Hou, B.; Wang, Y.; Liu, H. A resample-based SVA algorithm for sidelobe reduction of SAR/ISAR imagery with noninteger Nyquist sampling rate. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1016–1028. [Google Scholar] [CrossRef]
- Pastina, D.; Colone, F.; Lombardo, P. Effect of apodization on SAR image understanding. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3533–3551. [Google Scholar] [CrossRef]
- Jun, S.; Yang, L.; Xiaoling, Z.; Ling, F. A novel SAR sidelobe suppression method via Dual-Delta factorization. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1576–1580. [Google Scholar] [CrossRef]
- Fornaro, G.; Serafino, F.; Soldovieri, F. Three-dimensional focusing with multipass SAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 507–517. [Google Scholar] [CrossRef]
- Fornaro, G.; Guarnieri, A.M.; Pauciullo, A.; De-Zan, F. Maximum likelihood multi-baseline SAR interferometry. IEE Proc. Radar Sonar Navig. 2006, 153, 279–288. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Kuang, H.; Yang, W.; Liu, W.; Wang, P. A novel imaging algorithm for focusing high-resolution spaceborne SAR data in squinted sliding-spotlight mode. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1577–1581. [Google Scholar] [CrossRef]
- Reale, D.; Fornaro, G.; Pauciullo, A.; Zhu, X.; Bamler, R. Tomographic imaging and monitoring of buildings with very high resolution SAR data. IEEE Geosci. Remote Sens. Lett. 2011, 8, 661–665. [Google Scholar] [CrossRef]
- Sack, M.; Ito, M.R.; Cumming, I.G. Application of efficient linear FM matched filtering algorithms to synthetic aperture radar processing. Communications, Radar and Signal Processing. IEE Proc. F Commun. Radar Signal Process. 1985, 132, 45–57. [Google Scholar] [CrossRef]
- Zhu, X.; He, F.; Ye, F.; Dong, Z.; Wu, M. Sidelobe Suppression with Resolution Maintenance for SAR Images via Sparse Representation. Sensors 2018, 18, 1589. [Google Scholar] [CrossRef] [PubMed]







| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Aircraft Height | 20 km | Bandwidth | 80 MHz |
| Incidence Angle | 30° | Sample Rate | 100 MHz |
| Wavelength | 0.03 m | PRF | 70 Hz |
| Velocity | 100 m/s | Antenna Length | 4.0 m |
| Flight Angle | 2° | Pulse Duration | 10 |
| Baseline | 12 m | Flight passes | 31 |
| Single Point Target | Resolution | PSLR | ISLR |
|---|---|---|---|
| Rectangular Window | 1.99 m | −13.28 dB | −10.11 dB |
| Taylor Window | 2.49 m | −25.41 dB | −20.18 dB |
| Proposed Method | 1.85 m | −31.07 dB | −29.36 dB |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yang, W.; Chen, J.; Kuang, H.; Liu, W.; Li, C. Azimuth Sidelobes Suppression Using Multi-Azimuth Angle Synthetic Aperture Radar Images. Sensors 2019, 19, 2764. https://doi.org/10.3390/s19122764
Wang Y, Yang W, Chen J, Kuang H, Liu W, Li C. Azimuth Sidelobes Suppression Using Multi-Azimuth Angle Synthetic Aperture Radar Images. Sensors. 2019; 19(12):2764. https://doi.org/10.3390/s19122764
Chicago/Turabian StyleWang, Yamin, Wei Yang, Jie Chen, Hui Kuang, Wei Liu, and Chunsheng Li. 2019. "Azimuth Sidelobes Suppression Using Multi-Azimuth Angle Synthetic Aperture Radar Images" Sensors 19, no. 12: 2764. https://doi.org/10.3390/s19122764
APA StyleWang, Y., Yang, W., Chen, J., Kuang, H., Liu, W., & Li, C. (2019). Azimuth Sidelobes Suppression Using Multi-Azimuth Angle Synthetic Aperture Radar Images. Sensors, 19(12), 2764. https://doi.org/10.3390/s19122764







