Improving Optical Measurements: Non-Linearity Compensation of Compact Charge-Coupled Device (CCD) Spectrometers
Abstract
:1. Introduction
2. Theory
2.1. Design of a CCD Spectrometer
2.2. Signal Composition
2.2.1. ADC Offset
2.2.2. Dark Current
2.2.3. Non-Linearity
2.2.4. Blooming
2.2.5. Stray Light
2.2.6. Uncertainty of the Integration Time
2.2.7. Wavelength Calibration
2.2.8. Overall Signal Composition
3. Materials and Methods
3.1. Experimental Setup
3.2. Independent Linearity Test
4. Results and Discussion
4.1. ADC Offset
4.2. Correction of the Non-Linearity
4.3. Uncertainty in the Integration Time
4.4. Detector Noise
4.5. Using Curve Fitting to Reduce the Noise of the Detector
4.6. Temperature Dependency
4.7. Methodological Summary
- Determination of the ADC offset: calculate a linear regression of the dark spectra vs. integration time and calculate the dark current (in counts) at an integration time of zero. The result is the ADC offset (see Equation (1)) for the used spectrometer.
- Plot the intensity of a range of pixels versus the integration time to determine the level at which the signal response of the spectrometer becomes obviously non-linear (see Figure 7) and exclude all data above that threshold (e.g., 50,000 counts in the case of the Hamamatsu C10082CA) during all consecutive steps.
- Select a number of the pixels at high integration times where the intensities are close to the threshold and average these pixels to form the reference graph (Iraw(t)). Subtract wADC from all intensities of this intensity data curve and perform a linear regression (forced through zero). Calculate a corrected intensity (Icorr) for all integration times of the reference graph.
- There is now a value-pair of Iraw and Icorr for all integration times that can be used to formulate a relationship. In the R programming language, Equation (7)) would look like:“lm(yNew ~ 0 + y + I(y^2) + I(y^3) + I(y^4) + I(y^5) + I(y^6) + I(y^7) + I(y^8) + I(y^9))” with y = Iraw and yNew = Icorr (see Section 4.2).
- Use this function to calculate a linear corrected intensity (Icorr) for each raw intensity (Iraw) independent of the integration time.
- We determined the ADC offset first, which seems to be a key way of achieving better accuracy at low light conditions. This is done by forcing the linear regression through zero at zero integration time, using dark measurements, which is superior as it prevents inaccuracies caused by thermal noise.
- We excluded data where we knew that the response of the instrument was highly nonlinear (>50,000 counts) (see Figure 7). While this may not be an issue with the Ocean Optics spectrometers, this certainly is an issue for the CCD-based Hamamatsu units. It is possible to use the full range of minimum and maximum counts of the spectrometer. However, it should be considered during data analysis that the error behavior is different for different ranges of counts.
- We provided criteria as to which pixels to select for averaging to give a better performance for the correction (see Section 4.2.). These criteria are not provided by the OOINLCorrect Software [7] description.
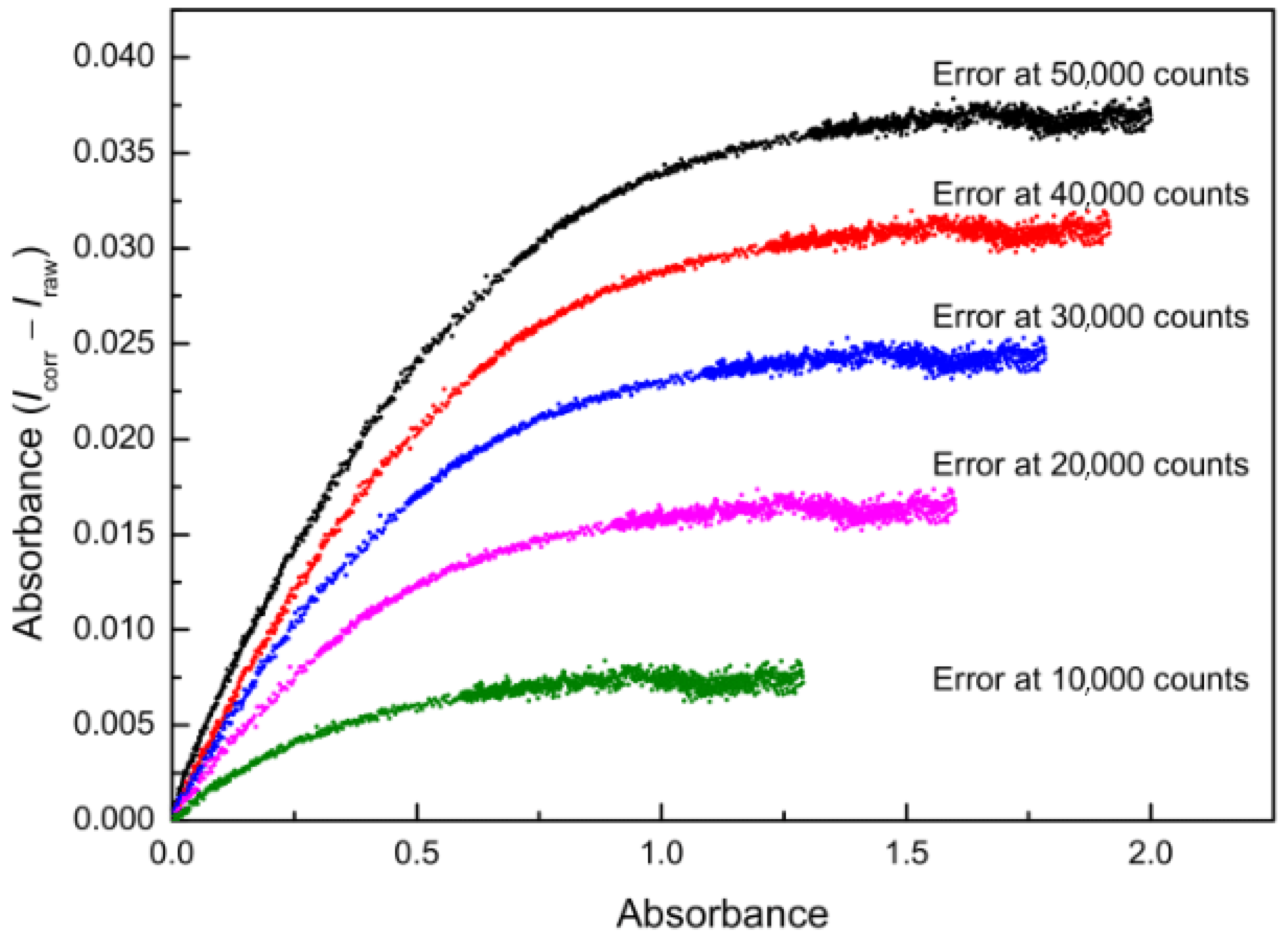
- We used absorption units instead of percentage for the evaluation of the changes in the results (see Figure 10). The example data show the benefits of our approach.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Available online: https://www.hamamatsu.com/eu/en/product/type/C10083CA/index.html (accessed on 7 January 2019).
- Oda, E.; Ishihara, Y.; Teranishi, N. Blooming suppression mechanism for an interline CCD image sensor with a vertical overflow drain. In Proceedings of the International Electron Devices Meeting, Washington, DC, USA, 5–7 December 1983; pp. 501–504. [Google Scholar]
- Li, L.; Dai, C.; Wu, Z.; Wang, Y. Temperature and Nonlinearity Correction Methods for Commercial CCD Array Spectrometers Used in Field. In Proceedings of the APPLIED OPTICS AND PHOTONICS CHINA (AOPC2017), Beijing, China, 4–6 June 2017; Volume 10463. [Google Scholar]
- Aßmann, S.; Frank, C.; Körtzinger, A. Spectrophotometric high-precision seawater pH determination for use in underway measuring systems. Ocean Sci. 2011, 7, 597–607. [Google Scholar] [CrossRef] [Green Version]
- Xia, G.; Liu, Q.; Zhou, H.; Yu, F. A non-linearity correction method of charge-coupled device array spectrometer. SPIE Int. Soc. Opt. Eng. 2015, 9677, 1–6. [Google Scholar] [CrossRef]
- Pulli, T.; Nevas, S.; El Gawhary, O.; van den Berg, S.; Askola, J.; Kärhä, P.; Manoocheri, F.; Ikonen, E. Nonlinearity characterization of array spectroradiometers for the solar UV measurements. Appl. Opt. 2017, 56, 3077–3086. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://oceanoptics.com/wp-content/uploads/OOINLCorrect-Linearity-Coeff-Proc.pdf (accessed on 10 April 2019).
- CCD, PDA Detector Definitions. Available online: http://www.horiba.com/us/en/scientific/products/oem-mini-ccd-spectrometers/ccds-photodiode-arrays/ccd-pda-detector-definitions/ (accessed on 11 January 2019).
- Neves, M.S.A.C.; Souto, M.R.S.; Tóth, I.V.; Victal, S.M.A.; Drumond, M.C.; Rangel, A.O.S.S. Spectrophotometric flow system using vanadomolybdophosphate detection chemistry and a liquid waveguide capillary cell for the determination of phosphate with improved sensitivity in surface and ground water samples. Talanta 2008, 77, 527–532. [Google Scholar] [CrossRef]
- Li, Y.; Hu, J.; Yang, J.; Zheng, B.; Ha, Y. Multi-component analysis by flow injection-diode array detection-spectrophotometry using partial least squares calibration model for simultaneous determination of zinc, cadmium and lead. Anal. Chim. Acta 2002, 461, 181–188. [Google Scholar]
- Frank, C.; Meier, D.; Voß, D.; Zielinski, O. Computation of nitrate concentrations in coastal waters using an in situ ultraviolet spectrophotometer: Behavior of different computation methods in a case study a steep salinity gradient in the southern North Sea. Methods Oceanogr. 2014, 9, 34–43. [Google Scholar] [CrossRef]
- Müller, J.D.; Schneider, B.; Aßmann, S.; Rehder, G. Spectrophotometric pH measurements in the presence of dissolved organic matter and hydrogen sulfide. Limnol. Oceanogr. Methods 2018, 16, 68–82. [Google Scholar] [CrossRef]
- Rérolle, V.M.C.; Floquet, C.F.A.; Mowlem, M.C.; Connelly, D.P.; Achterberg, E.P.; Bellerby, R.R.G.J. Seawater-pH measurements for ocean-acidification observations. TrAC Trends Anal. Chem. 2012, 40, 146–157. [Google Scholar] [CrossRef]
- Zielinski, O.; Voß, D.; Saworski, B.; Fiedler, B.; Körtzinger, A. Computation of nitrate concentrations in turbid coastal waters using an in situ ultraviolet spectrophotometer. J. Sea Res. 2011, 65, 456–460. [Google Scholar] [CrossRef]
- Pereyra, A.; Zevallos, M.I.; Ricra, J.; Tello, J.C. Characterizing a CCD detector for astronomical purposes: OAUNI Project. Rev. Tecnia 2016, 26, 20–25. [Google Scholar] [CrossRef]
- Seckmeyer, G.; Bais, A.; Bernhard, G.; Blumthaler, M.; Booth, C.; Disterhoft, P.; Eriksen, R.; McKenzie, M.; Miyauchi, M.; Roy, C. Instruments to Measure Solar Ultraviolet Radiation: Part 1: Spectral Instruments; World Meteorological Organization: Geneva, Switzerland, 2001. [Google Scholar]
- Seckmeyer, G.; Bais, A.; Bernhard, G.; Blumthaler, M.; Drüke, S.; Kiedron, P.; Lantz, K.; McKenzie, R.; Riechelmann, S. Instruments to Measure Solar Ultraviolet Radiation: Part 4: Array Spectroradiometers; World Meteorological Organization: Geneva, Switzerland, 2010. [Google Scholar]
- Canet-Ferrer, J.; Garcia-Calzada, R.; Martínez-Pastor, J.P.; Muñoz-Matutano, G. Stroboscopic Space Tag for Optical Time Resolved measurements with Charge Coupled Device detector. ACS Photonics 2019, 6, 181–188. [Google Scholar] [CrossRef]
- Smalley, D.; Poon, T.C.; Gao, H.; Kvavle, J.; Qaderi, K. Volumetric Displays: Turning 3-D Inside-Out. Opt. Photonics News 2018, 6, 26–33. [Google Scholar] [CrossRef]
- Davenport, J.J.; Hodgkinson, J.; Saffell, J.R.; Tatam, R.P. Noise analysis for CCD-based ultraviolet and visible spectrophotometry. Appl. Opt. 2015, 54, 8135–8144. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Xia, G.; Jin, S.; Hu, M.; Wu, S.; Xing, J. Denoising analysis of compact CCD-based spectrometer. Optik (Stuttg) 2018, 157, 693–706. [Google Scholar] [CrossRef]
- Bardoux, A.; Penquer, A.; Gilard, O.; Ecoffet, R.; Auvergne, M. Radiation effects on image sensors. In Proceedings of the International Conference on Space Optics (ICSO 2012), Corsica, France, 24–26 September 2012; Volume 10564. [Google Scholar]
- Cherniak, M.E.; Ulanova, A.V.; Nikiforov, A.Y. Analysis of the Effect of the Interline CCD-Sensor Dark Signal Increasing during Gamma-Irradiation. J. Phys. Conf. Ser. 2016, 737. [Google Scholar] [CrossRef]
- Wang, S.; Carpenter, D.A.; DeJager, A.; DiBella, J.A.; Doran, J.E.; Fabinski, R.P.; Garland, A.; Johnson, J.A.; Yaniga, R. A 47 million pixel high-performance interline CCD image sensor. IEEE Trans. Electron Devices 2016, 63, 174–181. [Google Scholar] [CrossRef]
- Fellers, T.J.; Davidson, M.W. Concepts in Digital Imaging Technology: CCD Saturation and Blooming. Available online: https://micro.magnet.fsu.edu/primer/digitalimaging/concepts/ccdsatandblooming.html (accessed on 11 January 2019).
- Salim, S.G.R.; Fox, N.P.; Hartree, W.S.; Woolliams, E.R.; Sun, T.; Grattan, K.T.V. Stray light correction for diode-array-based spectrometers using a monochromator. Appl. Opt. 2011, 50, 5130–5138. [Google Scholar] [CrossRef] [PubMed]
- Zong, Y.; Brown, S.W.; Johnson, B.C.; Lykke, K.R.; Ohno, Y. Simple spectral stray light correction method for array spectroradiometers. Appl. Opt. 2006, 45, 1111–1119. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.C.; Huang, C.; Xia, G.; Jin, S.Q.; Lu, H.B. Accurate wavelength calibration method for compact CCD spectrometer. J. Opt. Soc. Am. A 2017, 34, 498–505. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.hamamatsu.com/resources/pdf/ssd/s11071-1004_etc_kmpd1120e.pdf (accessed on 7 January 2019).
- Python Software Foundation. Python Language Reference, Version 3.7.1. Available online: http://www.python.org (accessed on 11 January 2019).
- Available online: http://www.R-project.org (accessed on 11 January 2019).

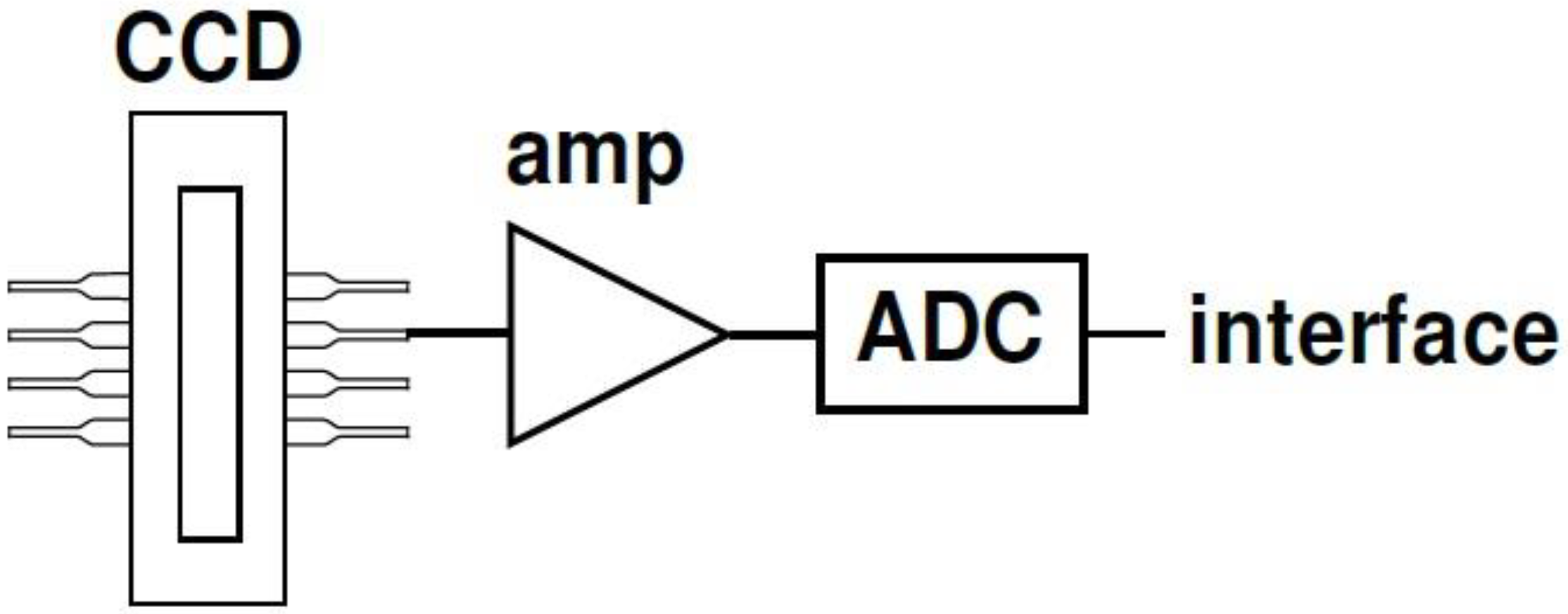









| Parameter | Hamamatsu C10082CA, S10420-1106-01 Series |
|---|---|
| Built-in sensor | Back-thinned CCD image sensor |
| Spectral range | 200–800 nm |
| Number of pixels | 2048 |
| A/D conversion | 16-bits |
| Integration time | 10 to 10,000 ms |
| Operating temperature | +5 to +40 °C |
| Cooling | Non-cooled CCD |
| Blooming | Anti-blooming function applied |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nehir, M.; Frank, C.; Aßmann, S.; Achterberg, E.P. Improving Optical Measurements: Non-Linearity Compensation of Compact Charge-Coupled Device (CCD) Spectrometers. Sensors 2019, 19, 2833. https://doi.org/10.3390/s19122833
Nehir M, Frank C, Aßmann S, Achterberg EP. Improving Optical Measurements: Non-Linearity Compensation of Compact Charge-Coupled Device (CCD) Spectrometers. Sensors. 2019; 19(12):2833. https://doi.org/10.3390/s19122833
Chicago/Turabian StyleNehir, Münevver, Carsten Frank, Steffen Aßmann, and Eric P. Achterberg. 2019. "Improving Optical Measurements: Non-Linearity Compensation of Compact Charge-Coupled Device (CCD) Spectrometers" Sensors 19, no. 12: 2833. https://doi.org/10.3390/s19122833
APA StyleNehir, M., Frank, C., Aßmann, S., & Achterberg, E. P. (2019). Improving Optical Measurements: Non-Linearity Compensation of Compact Charge-Coupled Device (CCD) Spectrometers. Sensors, 19(12), 2833. https://doi.org/10.3390/s19122833





