Optimal Deployment of Vector Sensor Nodes in Underwater Acoustic Sensor Networks
Abstract
:1. Introduction
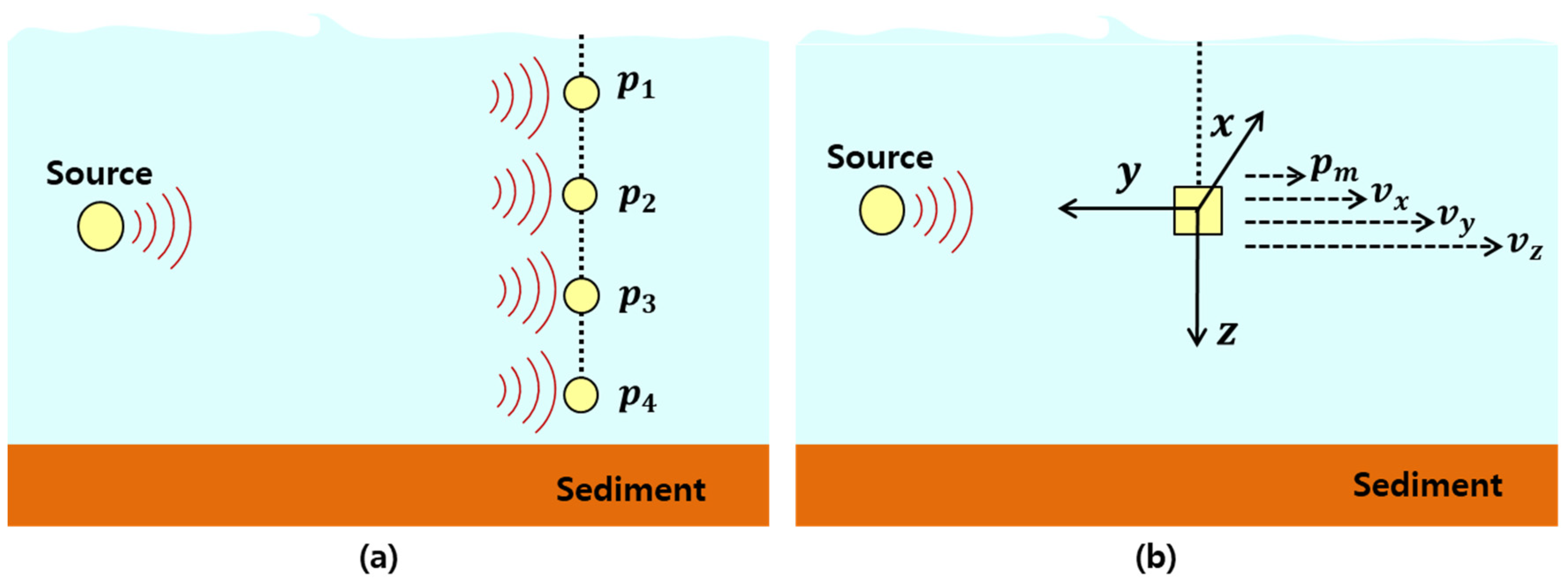
2. Communication Performance Based on Single-Vector Sensors
2.1. Summary of Previous Research
2.2. Underwater Acoustic Communication Using Single-Vector Sensors
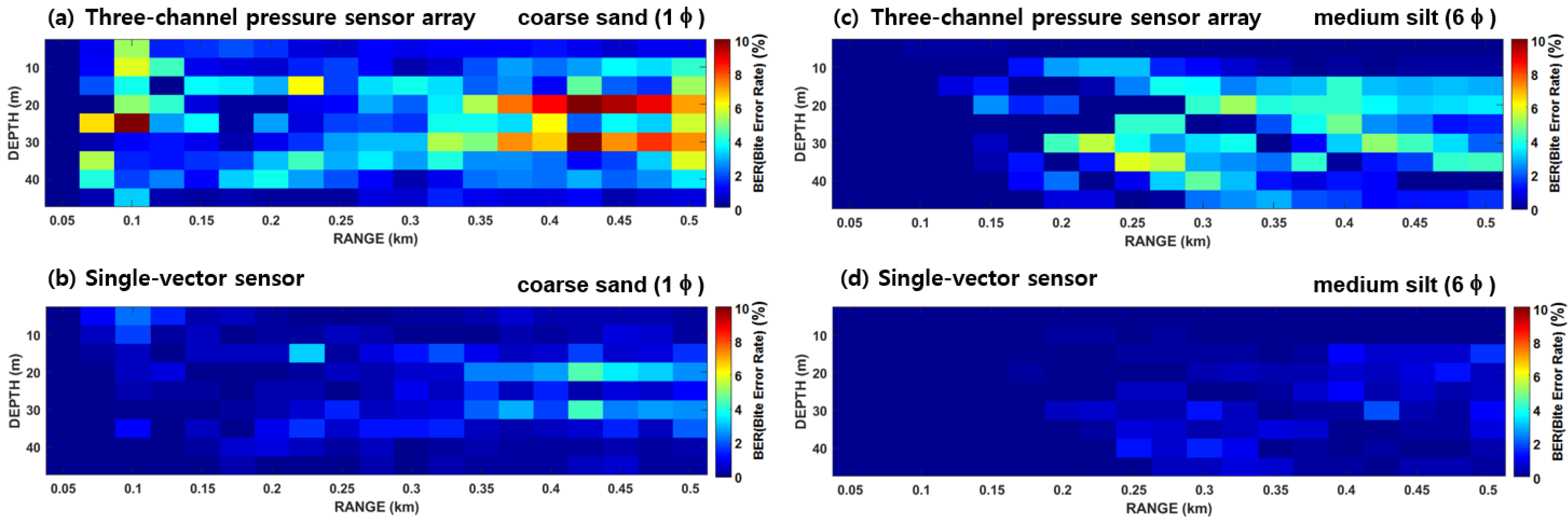
2.3. Communication PS Based on a Single-Vector Sensor
3. Optimal Deployment of Underwater Sensor Nodes
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Akyildiz, I.F.; Pompili, D.; Melodia, T. Underwater acoustic sensor networks: Research challenges. Ad. Hoc. Netw. 2005, 3, 257–279. [Google Scholar] [CrossRef]
- Lloret, J. Underwater sensor nodes and networks. Sensors 2013, 13, 11782–11796. [Google Scholar] [CrossRef] [PubMed]
- Pompili, D.; Melodia, T.; Akyildiz, I.F. Three-dimensional and two-dimensional deployment analysis for underwater acoustic sensor networks. Ad Hoc Netw. 2009, 7, 778–790. [Google Scholar] [CrossRef]
- Akkaya, K.; Newell, A. Self-deployment of sensors for maximized coverage in underwater acoustic sensor networks. Comput. Commun. 2009, 32, 1233–1244. [Google Scholar] [CrossRef]
- Kilfoyle, D.B.; Baggeroer, A.B. The State of the Art in Underwater Acoustic Telemetry. IEEE J. Ocean. Eng. 2000, 25, 4–27. [Google Scholar] [CrossRef]
- Du, H.; Xia, N.; Zheng, R. Particle swarm inspired underwater sensor self-deployment. Sensors 2014, 14, 15262–15281. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Guo, Z.; Dong, W.; Hong, F.; Zhao, Y. LDB. Localization with directional beacons for sparse 3D underwater acoustic sensor networks. J. Netw. 2010, 5, 28–38. [Google Scholar] [CrossRef]
- Choi, J.W.; Dahl, P.H. Measurement and simulation of the channel intensity impulse response for a site in the East China Sea. J. Acoust. Soc. Am. 2006, 119, 2677–2685. [Google Scholar] [CrossRef]
- Rouseff, D.; Badiey, M.; Song, A. Effect of reflected and refracted signals on coherent underwater acoustic communication: Results from the Kauai experiment (KauaiEx 2003). J. Acoust. Soc. Am. 2009, 126, 1359–2366. [Google Scholar] [CrossRef]
- Song, A.; Badey, M.; Song, S.C.; Hodgkiss, S.; Porter, M.B. Impact of ocean variability on coherent underwater acoustic communications during the Kauai experiment (KauaiEx). J. Acoust. Soc. Am. 2008, 123, 856–865. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Son, S.U.; Kim, H.; Choi, K.H.; Choi, J.W. Estimate of Passive Time Reversal Communication Performance in Shallow Water. Appl. Sci. 2018, 8, 23. [Google Scholar] [CrossRef]
- Sendra, S.; Lloret, J.; Jimenez, J.M.; Parra, L. Underwater acoustic modems. IEEE J. Sens. 2016, 16, 4063–4071. [Google Scholar] [CrossRef]
- Kim, S.; Choi, J.W. Optimal Deployment of Sensor Nodes Based on Performance Surface of Underwater Acoustic Communication. Sensors 2017, 17, 2389–2403. [Google Scholar]
- Porter, M.B.; Bucker, H.P. Gaussian beam tracing for computing ocean acoustic fields. J. Acoust. Soc. Am. 1987, 82, 1349–1359. [Google Scholar] [CrossRef]
- Stojanovic, M.; Catipovic, J.; Proakis, J.G. Adaptive multichannel combining and equalization for underwater acoustic communications. J. Acoust. Soc. Am. 1993, 94, 1621–1631. [Google Scholar] [CrossRef]
- Song, H.C.; Hodgkiss, S.; Kuperman, W.A.; Higley, W.J.; Raghukumar, K.; Akal, T. Spatial diversity in passive time reversal communications. J. Acoust. Soc. Am. 2006, 120, 2067–2076. [Google Scholar] [CrossRef]
- Dall’Osto, D.R.; Dahl, P.H.; Choi, J.W. Properties of the acoustic intensity vector field in a shallow water waveguide. J. Acoust. Soc. Am. 2012, 131, 2023–2035. [Google Scholar] [CrossRef] [PubMed]
- D’Spain, G.L.; Luby, J.C.; Wilson, G.R.; Gramann, R.A. Vector sensors and vector sensor line arrays: Comments on optimal array gain and detection. J. Acoust. Soc. Am. 2006, 120, 171–185. [Google Scholar] [CrossRef]
- Dall’Osto, D.R.; Choi, J.W.; Dahl, P.H. Measurement of acoustic particle motion in shallow water and its application to geoacoustic inversion. J. Acoust. Soc Am. 2016, 139, 311–319. [Google Scholar] [CrossRef]
- Hawkes, M.; Nehorai, A. Acoustic Vector-Sensor Correlations in Ambient Noise. IEEE J. Ocean. Eng. 2001, 26, 337–347. [Google Scholar] [CrossRef]
- Cray, B.A.; Nuttall, A.H. Directivity factors for linear arrays of velocity sensors. J. Acoust. Soc. Am. 2001, 110, 324–331. [Google Scholar] [CrossRef]
- Song, A.; Abdi, A.; Badiey, M.; Hursky, P. Experimental Demonstration of Underwater Acoustic Communication by Vector Sensors. IEEE J. Ocean. Eng. 2011, 36, 454–461. [Google Scholar] [CrossRef]
- Abdi, A.; Guo, H. A New Compact Multichannel Receiver for Underwater Wireless Communication Networks. IEEE Trans. Commun. 2009, 8, 3326–3329. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H.; Jung, S.; Choi, J.W. Time reversal communication using vertical particle velocity and pressure signal in shallow water. Ad. Hoc. Netw. 2019, 89, 161–169. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Ma, J.J. An improved co-evolutionary particle swarm optimization for wireless sensor networks with dynamic deployment. Sensors 2007, 7, 354–370. [Google Scholar] [CrossRef]
- Proakis, J.G. Digital Communications; McGraw Hill: New York, NY, USA, 2008; pp. 298–315. [Google Scholar]
- Stojanovic, M.; Catipovic, J.A.; Proakis, J.G. Phase-Coherent Digital Communications for Underwater Acoustic Channels. IEEE J. Ocean. Eng. 1993, 19, 100–111. [Google Scholar] [CrossRef]
- Fahy, F.J. Sound Intensity; E&FN Spon: London, UK, 1995; pp. 1053–1075. [Google Scholar]
- McDowell, P. Environmental and Statistical Performance Mapping Model for Underwater Acoustic Detection Systems. Ph.D. Thesis, University of New Orleans, New Orleans, LA, USA, 2010. [Google Scholar]
- Chen, J.; Li, S.; Sun, Y. Novel Deployment Schemes for Mobile Sensor Networks. Sensors 2007, 7, 2907–2919. [Google Scholar] [CrossRef] [Green Version]
- Zou, Y.; Chakrabarty, K. Sensor deployment and target localization based on virtual forces. In Proceedings of the IEEE INFOCOM 2003. Twenty-Second Annual Joint Conference of the IEEE Computer and Communications Societies (IEEE Cat. No.03CH37428), San Francisco, CA, USA, 30 March–3 April 2003. [Google Scholar]
- Majid, A.S.; Joelianto, E. Optimal Sensor Deployment in Non-Convex Region using Discrete Particle Swarm Optimization Algorithm. In Proceedings of the IEEE Conference on Control, Systems & Industrial Informatics, Bandung, Indonesia, 23–26 September 2012. [Google Scholar]
- Wang, X.; Ma, J.; Wang, S.; Bi, D.W. Distributed particle swarm optimization and simulated annealing for energy-efficient coverage in wireless sensor networks. Sensors 2007, 7, 628–648. [Google Scholar] [CrossRef]




| Ocean Environmental Parameters | Value | Communication Parameters | Value |
|---|---|---|---|
| Month | February | Symbol number | 3500 |
| Longitude direction distance | 22 km | Symbol rate | 1000 sps |
| Latitude direction distance | 22 km | Pulse shaping | Root Raised Cosine filter |
| Wind speed | 10 m/s | Equalizer | Adaptive DFE (RLS) |
| Azimuth angle interval | 45° | BER criterion | 2% |
| Grid points | 100 | ||
| Channel Modeling Parameters | Value | ||
| Frequency | 10 kHz | ||
| Source level | 140 dB | ||
| Source depth | 2 m above the bottom | ||
| Three-channel vertical-pressure sensor array | Sensor depth | 0.5–3.5 m above the bottom | |
| Element spacing | 1.5 m (10 ) | ||
| Single-vector sensor | Sensor depth | 2 m above the bottom | |
| Optimal Deployment Parameters | Value |
|---|---|
| Loop number | 50 |
| Sensor node number | 100 |
| Attractive force weight | 0.01 |
| Repulsive force weight | 0.5 |
| Acceleration weight | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Choi, J.W. Optimal Deployment of Vector Sensor Nodes in Underwater Acoustic Sensor Networks. Sensors 2019, 19, 2885. https://doi.org/10.3390/s19132885
Kim S, Choi JW. Optimal Deployment of Vector Sensor Nodes in Underwater Acoustic Sensor Networks. Sensors. 2019; 19(13):2885. https://doi.org/10.3390/s19132885
Chicago/Turabian StyleKim, Sunhyo, and Jee Woong Choi. 2019. "Optimal Deployment of Vector Sensor Nodes in Underwater Acoustic Sensor Networks" Sensors 19, no. 13: 2885. https://doi.org/10.3390/s19132885
APA StyleKim, S., & Choi, J. W. (2019). Optimal Deployment of Vector Sensor Nodes in Underwater Acoustic Sensor Networks. Sensors, 19(13), 2885. https://doi.org/10.3390/s19132885






