Locating Underground Pipe Using Wideband Chaotic Ground Penetrating Radar
Abstract
1. Introduction
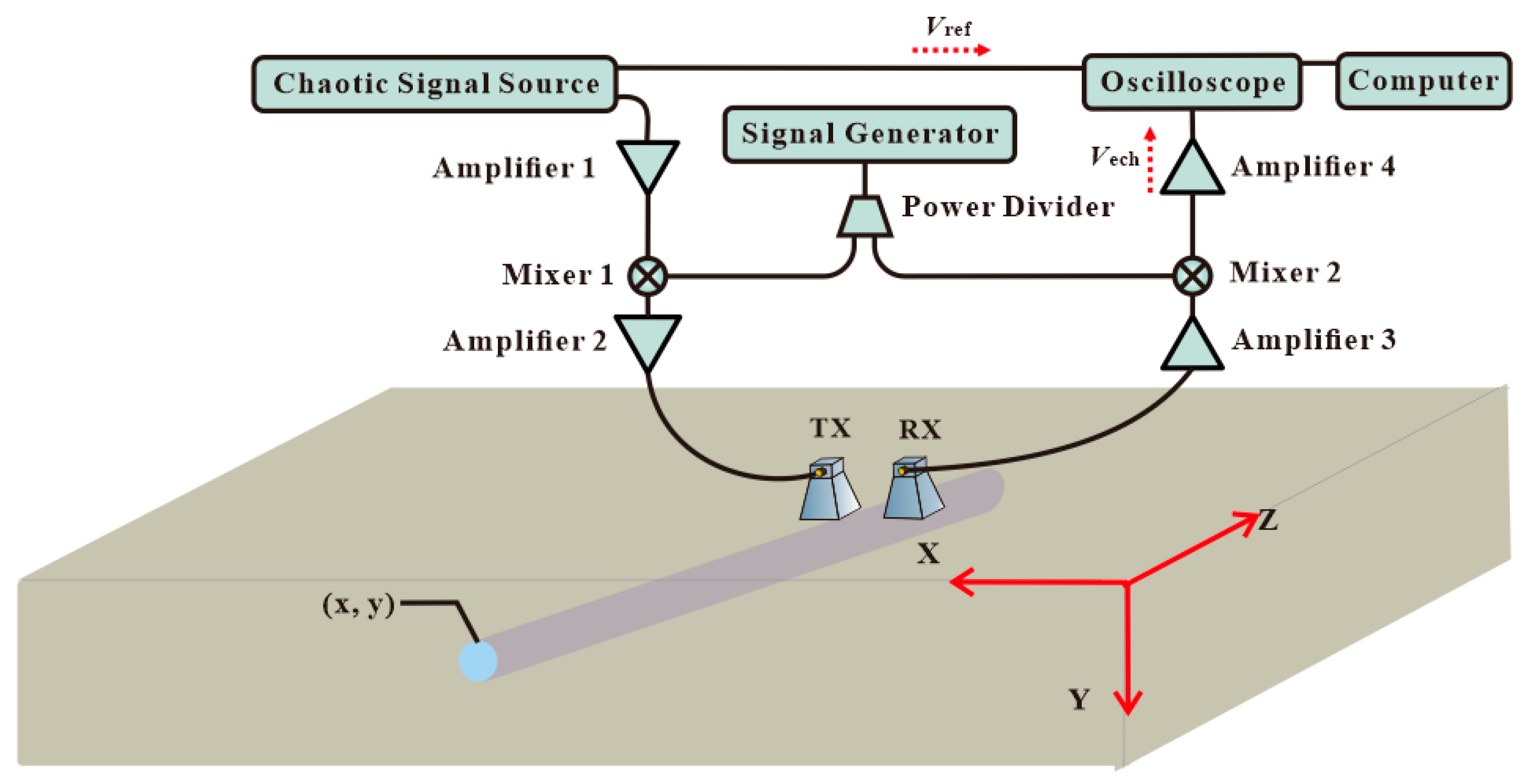
2. The Chaotic Radar System
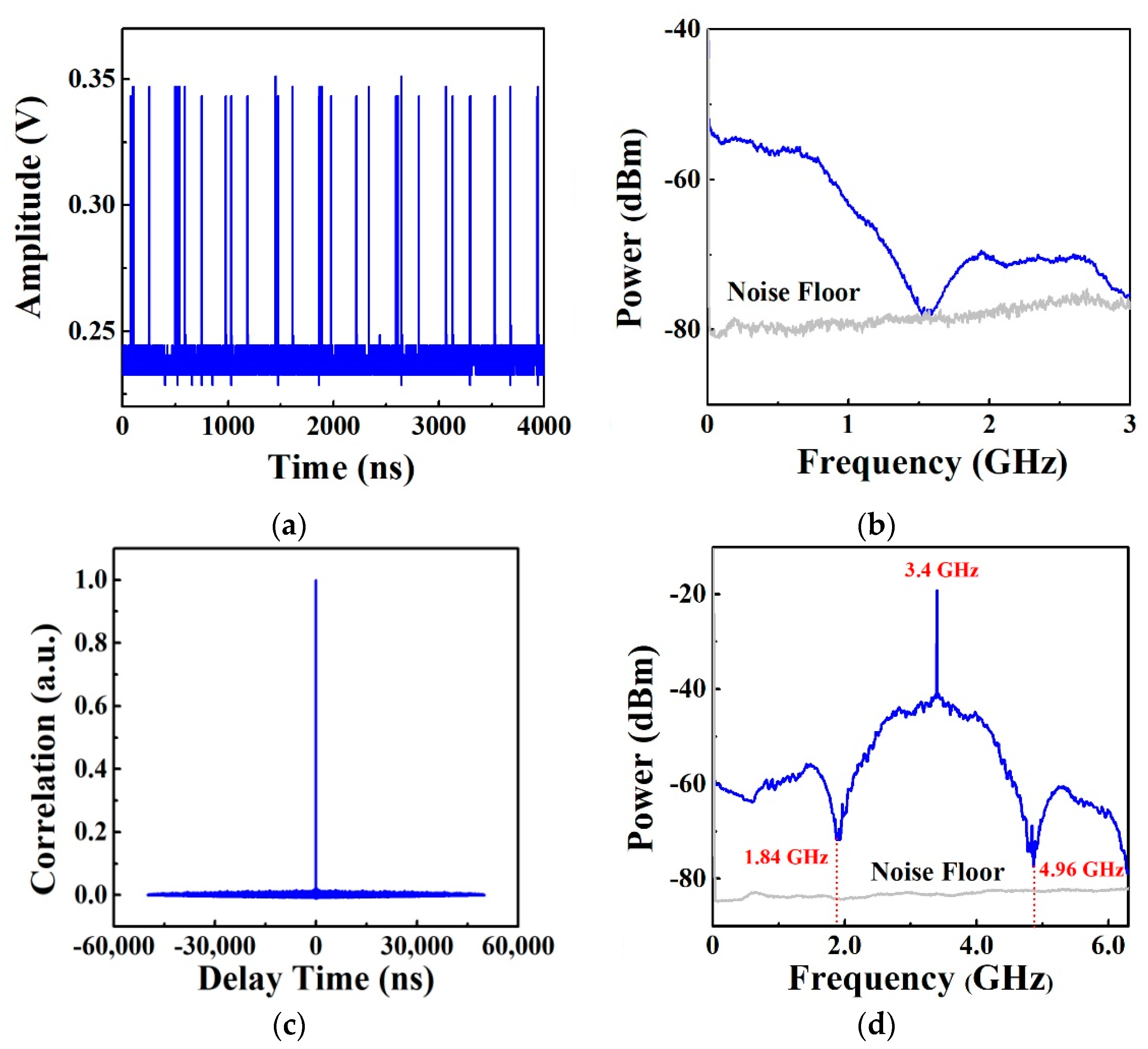
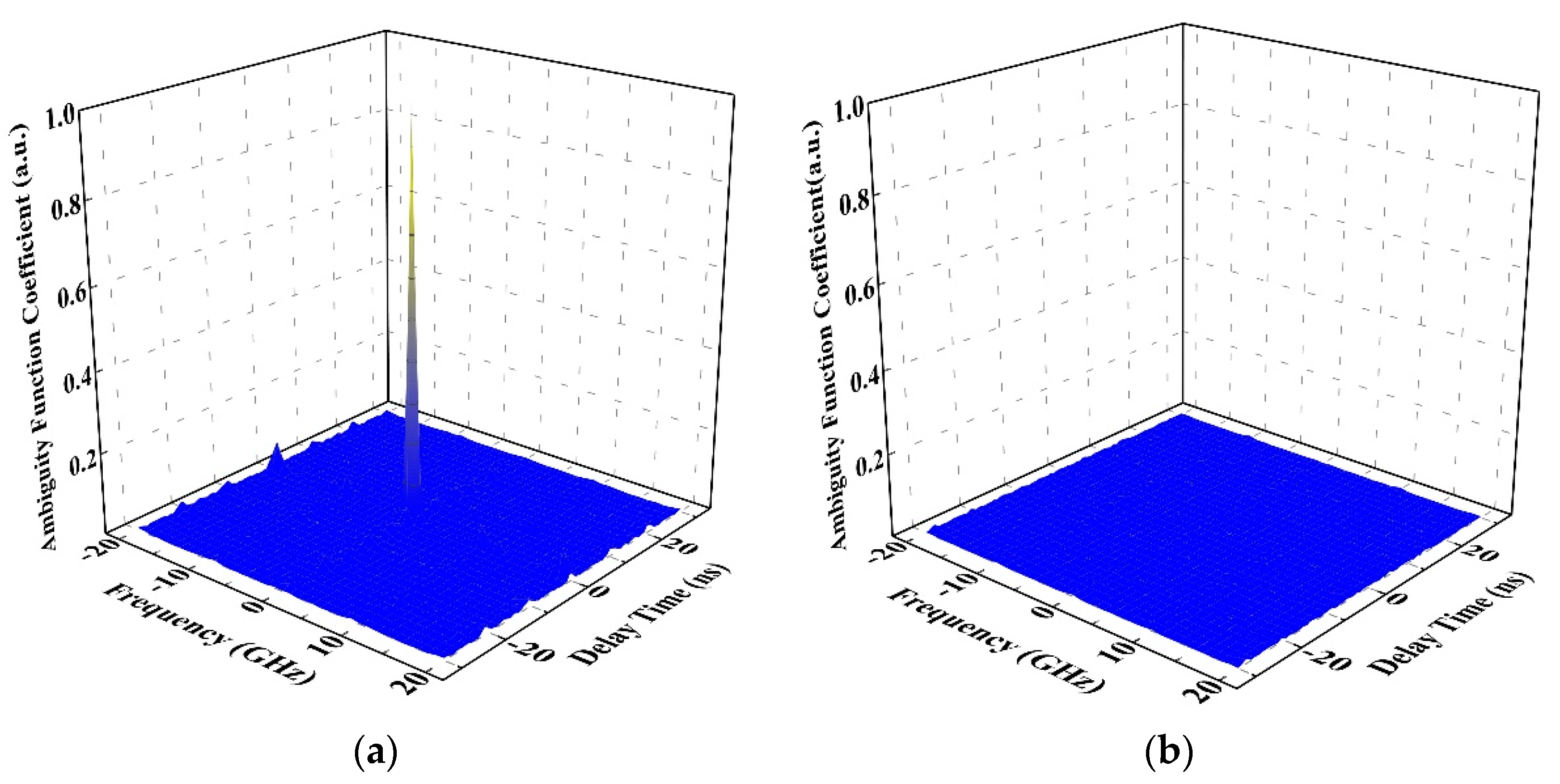
3. Characteristics of the Probe Signal
4. Experimental Results
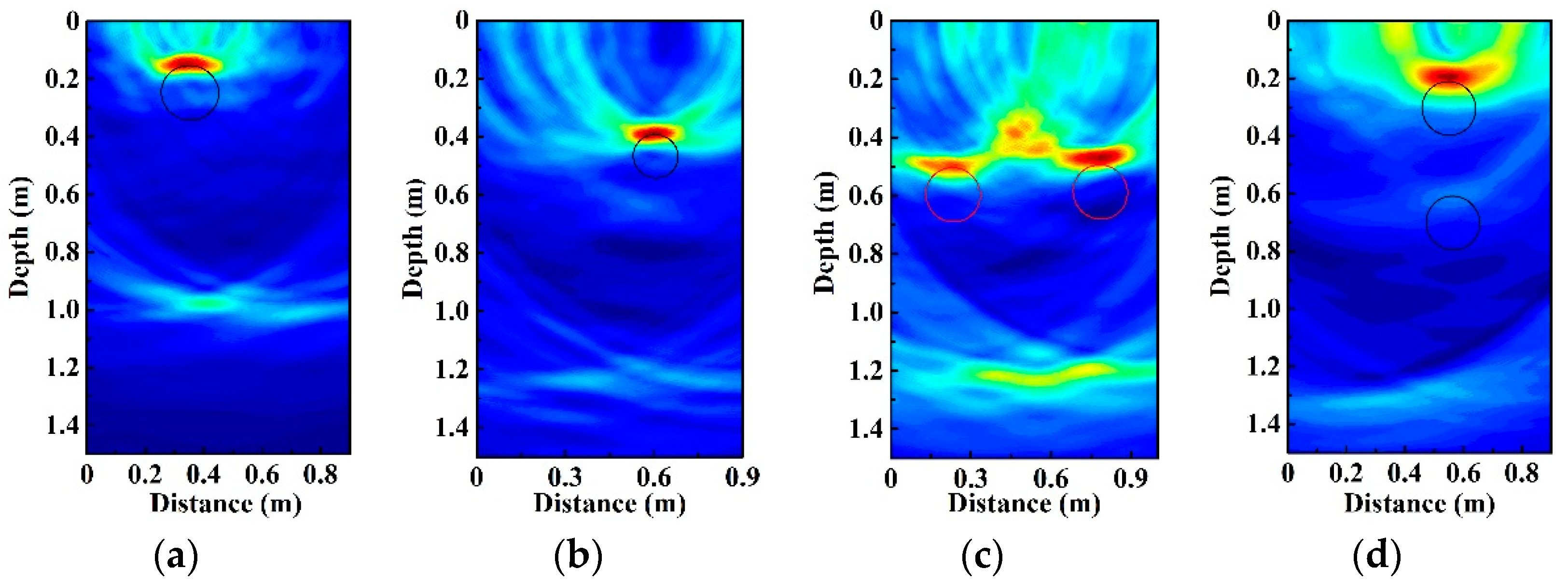
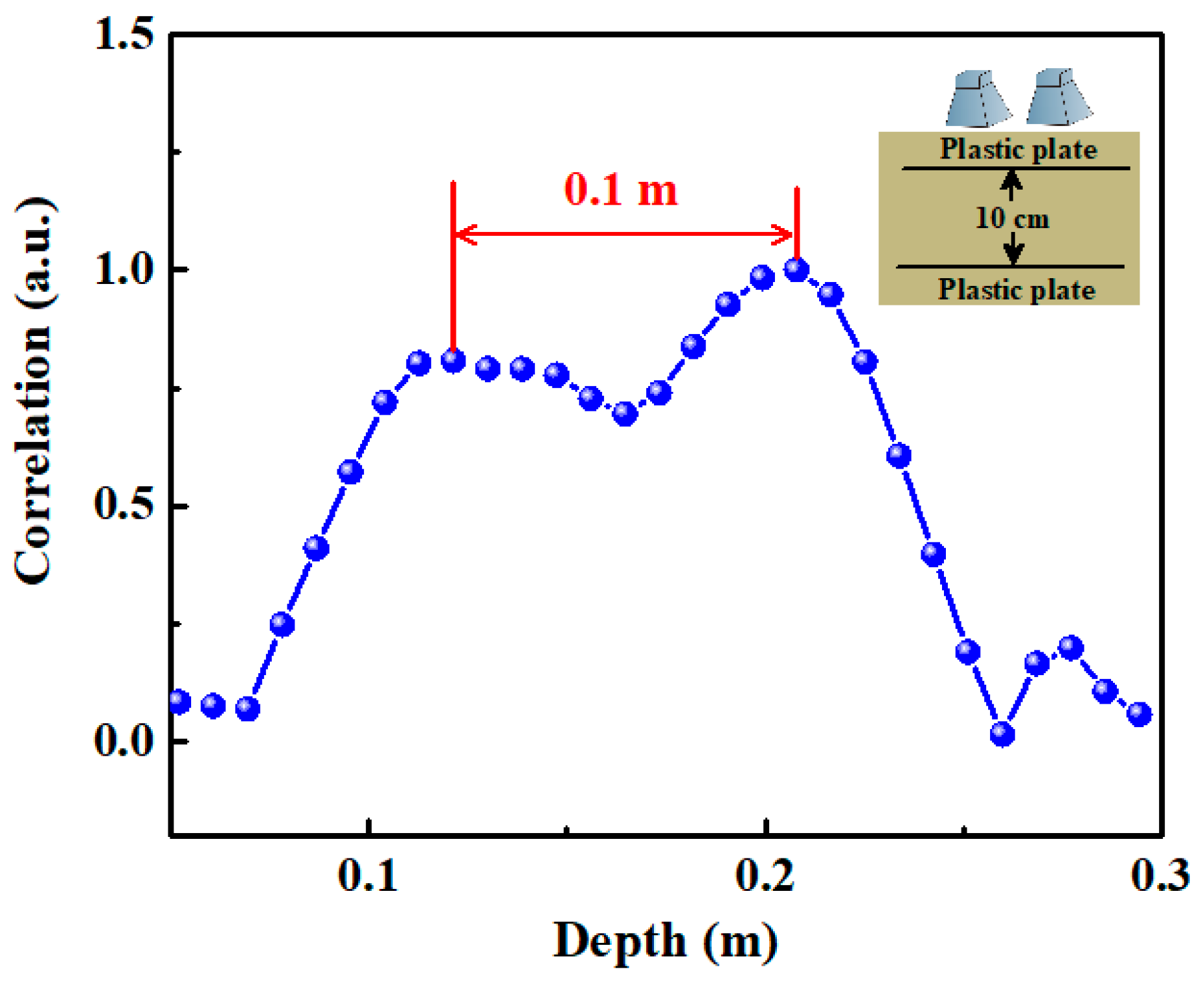
4.1. Plastic Pipe Location
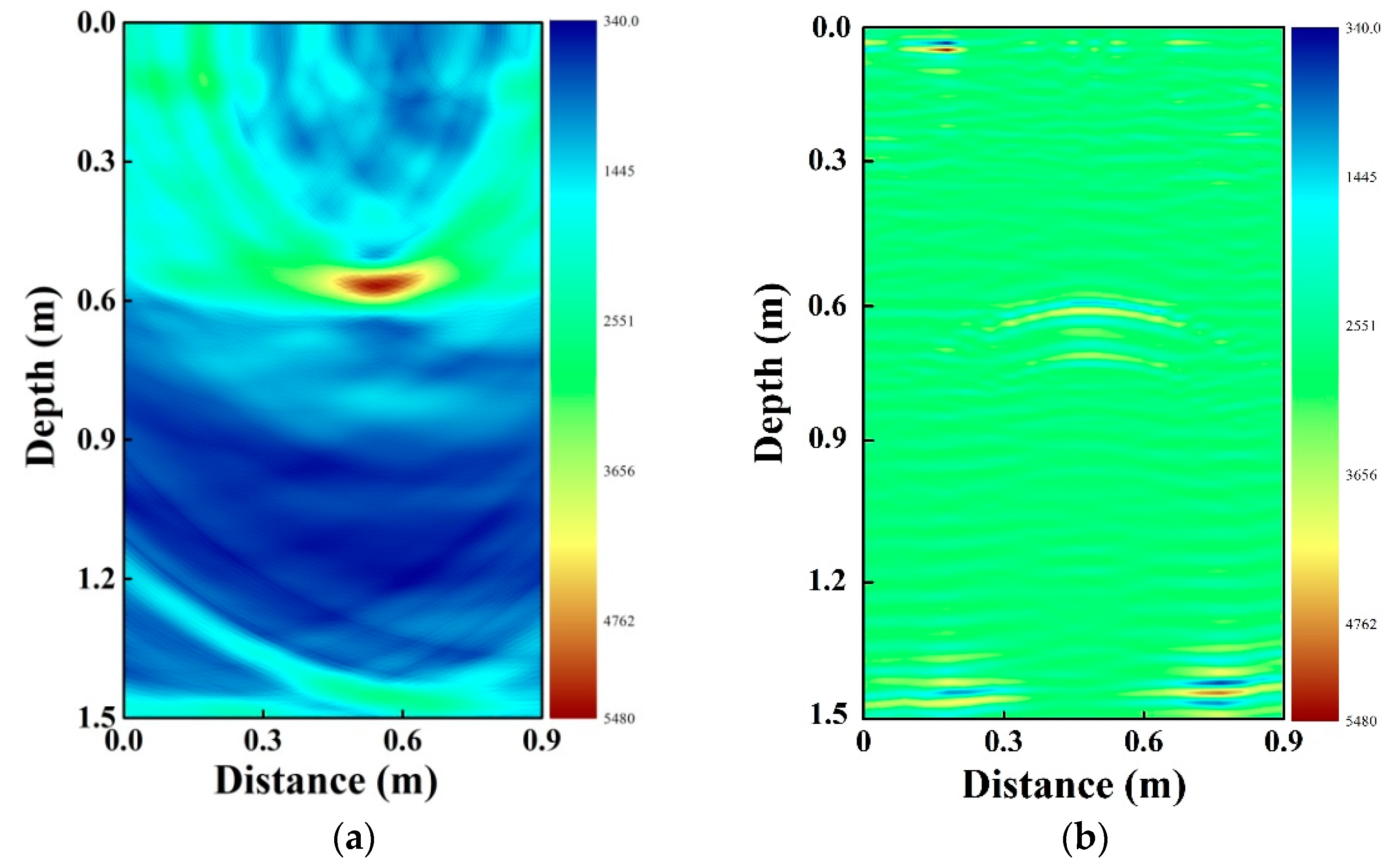
4.2. Metallic Pipe Location
4.3. Detection Performance
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gao, Y.; Brennan, M.; Joseph, P.F.; Muggleton, J.M.; Hunaidi, O. On the selection of acoustic/vibration sensors for leak detection in plastic water pipes. J. Sound Vib. 2005, 283, 927–941. [Google Scholar] [CrossRef]
- Brennan, M.J.; Joseph, P.J.; Muggleton, J.M.; Gao, Y. The use of acoustic methods to detect water leaks in buried water pipes. Water Sewerage J. 2006, 1, 11–13. [Google Scholar]
- Stoianov, I.; Nachman, L.; Madden, S.; Tokmouline, T.; Csail, M. PIPENETa wireless sensor network for pipeline monitoring. In Proceedings of the 6th International Conference on Information Processing in Sensor Networks, Cambridge, MA, USA, 25–27 April 2007; pp. 264–273. [Google Scholar]
- Choi, M.; Kang, K.; Park, J.; Kim, W.; Kim, K. Quantitative determination of a subsurface defect of reference specimen by lock-in infrared thermography. NDT E Int. 2008, 41, 119–124. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Srivastava, G.P. Characterisation of metal loss defects from magnetic flux leakage signals with discrete wavelet transform. NDT E Int. 2000, 33, 57–65. [Google Scholar] [CrossRef]
- Saha, S.; Mukhopadhyay, S.; Mahapatra, U.; Bhattacharya, S.; Srivastava, G.P. Empirical structure for characterizing metal loss defects from radial magnetic flux leakage signal. NDT E Int. 2010, 43, 507–512. [Google Scholar] [CrossRef]
- Angani, C.S.; Park, D.G.; Kim, C.G.; Leela, P.; Kishore, M.; Cheong, Y.M. Pulsed eddy current differential probe to detect the defects in a stainless steel pipe. J. Appl. Phys. 2011, 109, 07D348. [Google Scholar] [CrossRef]
- Rifai, D.; Abdalla, A.; Razali, R.; Ali, K.; Faraj, M. An eddy current testing platform system for pipe defect inspection based on an optimized eddy current technique probe design. Sensors 2017, 17, 579. [Google Scholar] [CrossRef] [PubMed]
- Park, B.; Kim, J.; Lee, J.; Kang, M.S.; An, Y.K. Underground object classification for urban roads using instantaneous phase analysis of Ground-Penetrating Radar (GPR) Data. Remote Sens. 2018, 10, 1417. [Google Scholar] [CrossRef]
- Hoarau, Q.; Ginolhac, G.; Atto, A.M.; Nicolas, J.M.; Ovarlez, J.P. Robust adaptive detection of buried pipes using GPR. Signal Process. 2017, 132, 293–305. [Google Scholar] [CrossRef]
- Zhu, H.; Yuen, K.V.; Mihaylova, L.; Leung, H. Overview of environment perception for intelligent vehicles. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2584–2601. [Google Scholar] [CrossRef]
- Huuskonen-Snicker, E.; Mikhnev, V.A.; Olkkonen, M.K. Discrimination of buried objects in impulse GPR using phase retrieval technique. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1001–1007. [Google Scholar] [CrossRef]
- Agrawal, S.; George, N.V.; Prashant, A. GPR data analysis of weak signals using modified s-transform. Geotech. Geol. Eng. 2015, 33, 1167–1182. [Google Scholar] [CrossRef]
- Brunzell, H. Detection of shallowly buried objects using impulse radar. IEEE Trans. Geosci. Remote Sens. 1999, 37, 875–886. [Google Scholar] [CrossRef]
- Geroleo, F.G.; Brandt-Pearce, M. Detection and estimation of LFMCW radar signals. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 405–418. [Google Scholar] [CrossRef]
- Wang, G.; Munoz-Ferreras, J.M.; Gu, C.; Li, C.; Gómez-García, R. Application of linear-frequency-modulated continuous-wave (LFMCW) radars for tracking of vital signs. IEEE Trans. Microw. Theory Tech. 2014, 62, 1387–1399. [Google Scholar] [CrossRef]
- Metje, N.; Atkins, P.R.; Brennan, M.J.; Chapman, D.N.; Lim, H.M.; Machell, J.; Muggleton, J.M.; Pennock, S.; Ratcliffe, J.; Redfern, M.; et al. Mapping the Underworld—State-of-the-Art Review. Tunn. Undergr. Space Technol. 2007, 22, 568–586. [Google Scholar] [CrossRef]
- Gurbuz, A.C.; McClellan, J.H.; Scott, W.R. A compressive sensing data acquisition and imaging method for stepped frequency GPRs. IEEE Trans. Signal Process. 2009, 57, 2640–2650. [Google Scholar] [CrossRef]
- Gallagher, K.A.; Phelan, B.R.; Sherbondy, K.D.; Narayanan, R.M. Performance analysis of forward-looking GPR ultra-wideband antennas for buried object detection. First Break 2015, 33, 51–59. [Google Scholar] [CrossRef]
- Liu, T.; Zhu, Y.; Su, Y. Method for compensating signal attenuation using stepped-frequency ground penetrating radar. Sensors 2018, 18, 1366. [Google Scholar] [CrossRef]
- Xu, X.; Xia, T.; Venkatachalam, A.; Huston, D. Development of high-speed ultrawideband ground-penetrating radar for rebar detection. J. Eng. Mech. 2012, 139, 272–285. [Google Scholar] [CrossRef]
- Li, L.; Tan, A.E.C.; Jhamb, K.; Rambabu, K. Buried object characterization using ultra-wideband ground penetrating radar. IEEE Trans. Microw. Theory Tech. 2012, 60, 2654–2664. [Google Scholar] [CrossRef]
- Soldovieri, F.; Lopera, O.; Lambot, S. Combination of advanced inversion techniques for an accurate target localization via GPR for demining applications. IEEE Trans. Geosci. Remote Sens. 2010, 49, 451–461. [Google Scholar] [CrossRef]
- Morrow, I.L.; Genderen, P. Effective imaging of buried dielectric objects. IEEE Trans. Geosci. Remote Sens. 2002, 40, 943–949. [Google Scholar] [CrossRef]
- Salucci, M.; Poli, L.; Massa, A. Advanced multi-frequency GPR data processing for non-linear deterministic imaging. Signal Process. 2017, 132, 306–318. [Google Scholar] [CrossRef]
- Bevacqua, M.T.; Isernia, T. Shape reconstruction via equivalence principles, constrained inverse source problems and sparsity promotion. Prog. Electromagn. Res. 2017, 158, 37–48. [Google Scholar] [CrossRef]
- Liu, H.; Long, Z.; Tian, B.; Han, F.; Fang, G.; Liu, Q.H. Two-dimensional reverse-time migration applied to GPR with a 3-D-to-2-D data conversion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4313–4320. [Google Scholar] [CrossRef]
- Hugenschmidt, J.; Kalogeropoulos, A.; Soldovieri, F.; Prisco, G. Processing strategies for high-resolution GPR concrete inspections. NDT E Int. 2010, 43, 334–342. [Google Scholar] [CrossRef]
- Salucci, M.; Anselmi, N.; Oliveri, G.; Calmon, P.; Miorelli, R.; Reboud, C.; Massa, A. Real-time NDT-NDE through an innovative adaptive partial least squares SVR inversion approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6818–6832. [Google Scholar] [CrossRef]
- Wu, Y.; Shen, F.; Yuan, Y.; Xu, D. An improved modified universal ultra-wideband antenna designed for step frequency continuous wave ground penetrating radar system. Sensors 2019, 19, 1045. [Google Scholar] [CrossRef]
- Rahman, M.U.; NaghshvarianJahromi, M.; Mirjavadi, S.S.; Hamouda, A.M. Resonator based switching technique between ultra wide band (UWB) and single/dual continuously tunable-notch behaviors in UWB radar for wireless vital signs monitoring. Sensors 2018, 18, 3330. [Google Scholar] [CrossRef]
- Rahman, M.U.; NaghshvarianJahromi, M.; Mirjavadi, S.S.; Hamouda, A.M. Bandwidth enhancement and frequency scanning array antenna using novel UWB filter integration technique for OFDM UWB radar applications in wireless vital signs monitoring. Sensors 2018, 18, 3155. [Google Scholar] [CrossRef] [PubMed]
- Axelsson, S.R.J. Noise radar using random phase and frequency modulation. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2370–2384. [Google Scholar] [CrossRef]
- Utsi, V. Design of a GPR for deep investigations. In Proceeding of the 2007 4th International Workshop on Advanced Ground Penetrating Radar, Aula Magna Partenope, Italy, 27–29 June 2007; pp. 222–225. [Google Scholar]
- Sun, H.; Lu, Y.; Liu, G. Ultra-wideband technology and random signal radar: An ideal combination. IEEE Aerosp. Electron. Syst. Mag. 2003, 18, 3–7. [Google Scholar]
- Narayanan, R.M.; Xu, Y.; Hoffmeyer, P.D.; Curtis, J.O. Design and performance of a polarimetric random noise radar for detection of shallow buried targets. In Proceedings of the Detection Technologies for Mines and Minelike Targets, Orlando, FL, USA, 17–21 April 1995; pp. 20–31. [Google Scholar]
- Xu, Y.; Narayanan, R.M.; Xu, X.; Curtis, J.O. Polarimetric processing of coherent random noise radar data for buried object detection. IEEE Trans. Geosci. Remote Sens. 2001, 39, 467–478. [Google Scholar] [CrossRef]
- Tomizawa, Y.; Arai, I. Coded pulse signal subsurface radar. Electron. Commun. Jpn. 2002, 85, 8–16. [Google Scholar] [CrossRef]
- Arai, I.; Tomizawa, Y.; Hirose, M. Pulse compression subsurface radar. IEICE Trans. Commun. 2000, 83, 1930–1937. [Google Scholar]
- Lin, F.Y.; Liu, J.M. Chaotic radar using nonlinear laser dynamics. IEEE J. Quantum Electron. 2004, 40, 815–820. [Google Scholar] [CrossRef]
- Blakely, J.N.; Corron, N.J. Concept for low-cost chaos radar using coherent reception. In Proceedings of the Radar Sensor Technology XV, Orlando, FL, USA, 25–27 April 2011; pp. 80211H 1–80211H 7. [Google Scholar]
- Venkatasubramanian, V.; Leung, H.; Liu, X. Chaos UWB radar for through-the-wall imaging. IEEE Trans. Image Process. 2009, 18, 1255–1265. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Ji, Y.; Zhang, Y.; Wu, Y.; Xu, H.; Xu, W. Remote radar based on chaos generation and radio over fiber. IEEE Photonics J. 2014, 6, 1–12. [Google Scholar]
- Wang, B.; Xu, H.; Yang, P.; Liu, L.; Li, J. Target detection and ranging through lossy media using chaotic radar. Entropy 2015, 17, 2082–2093. [Google Scholar] [CrossRef]
- Liu, L.; Guo, C.; Li, J.; Xu, H.; Zhang, J.; Wang, B. Simultaneous life detection and localization using a wideband chaotic signal with an embedded tone. Sensors 2016, 16, 1866. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Leung, H. A novel chaos-based high-resolution imaging technique and its application to through-the-wall imaging. IEEE Signal Process. Lett. 2005, 12, 528–531. [Google Scholar] [CrossRef]
- Liu, L.; Ma, R.; Li, J.; Zhang, J.; Wang, B. Anti-jamming property of Colpitts-based direct chaotic through-wall imaging radar. J. Electromagn. Waves Appl. 2016, 30, 2268–2279. [Google Scholar] [CrossRef]
- Lin, F.Y.; Liu, J.M. Chaotic lidar. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 991–997. [Google Scholar] [CrossRef]
- Rao, S.S.; Howard, S.P. Correlation performance of chaotic signals in spread spectrum systems. In Proceedings of the IEEE Digital Signal Processing Workshop, Loen, Norway, 1–4 September 1996; pp. 506–509. [Google Scholar]
- Wang, A.B.; Wang, Y.C. Chaos correlation optical time domain reflectometry. Sci. China Inf. Sci. 2010, 53, 398–404. (In Chinese) [Google Scholar] [CrossRef]
- Xu, H.; Wang, B.; Zhang, J.; Liu, L.; Li, Y.; Wang, Y.; Wang, A. Chaos through-wall imaging radar. Sens. Imaging 2017, 18, 6–19. [Google Scholar] [CrossRef]
- Vazquez-Medina, R.; Díaz-Méndez, A.; del Río-Correa, J.L.; López-Hernández, J. Design of chaotic analog noise generators with logistic map and MOS QT circuits. Chaos Solitons Fractals 2009, 40, 1779–1793. [Google Scholar] [CrossRef]
- Xu, H.; Wang, B.; Li, J.; Wang, A.; Wang, Y. Location of wire faults using chaotic signal generated by an improved Colpitts oscillator. Int. J. Bifurc. Chaos 2014, 24, 1450053. [Google Scholar] [CrossRef]



| Pipes | Aliasing | Diameter (m) | Length (m) | Thickness (mm) |
|---|---|---|---|---|
 | Plastic 1 | 0. 20 | 0.52 | 3 |
 | Plastic 2 | 0.15 | 0.60 | 4 |
 | Metallic 1 | 0.10 | 0.60 | 2 |
 | Metallic 2 | 0.05 | 0.35 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Guo, T.; Leung, H.; Xu, H.; Liu, L.; Wang, B.; Liu, Y. Locating Underground Pipe Using Wideband Chaotic Ground Penetrating Radar. Sensors 2019, 19, 2913. https://doi.org/10.3390/s19132913
Li J, Guo T, Leung H, Xu H, Liu L, Wang B, Liu Y. Locating Underground Pipe Using Wideband Chaotic Ground Penetrating Radar. Sensors. 2019; 19(13):2913. https://doi.org/10.3390/s19132913
Chicago/Turabian StyleLi, Jingxia, Tian Guo, Henry Leung, Hang Xu, Li Liu, Bingjie Wang, and Yang Liu. 2019. "Locating Underground Pipe Using Wideband Chaotic Ground Penetrating Radar" Sensors 19, no. 13: 2913. https://doi.org/10.3390/s19132913
APA StyleLi, J., Guo, T., Leung, H., Xu, H., Liu, L., Wang, B., & Liu, Y. (2019). Locating Underground Pipe Using Wideband Chaotic Ground Penetrating Radar. Sensors, 19(13), 2913. https://doi.org/10.3390/s19132913






