Resonant Grating without a Planar Waveguide Layer as a Refractive Index Sensor
Abstract
:1. Introduction
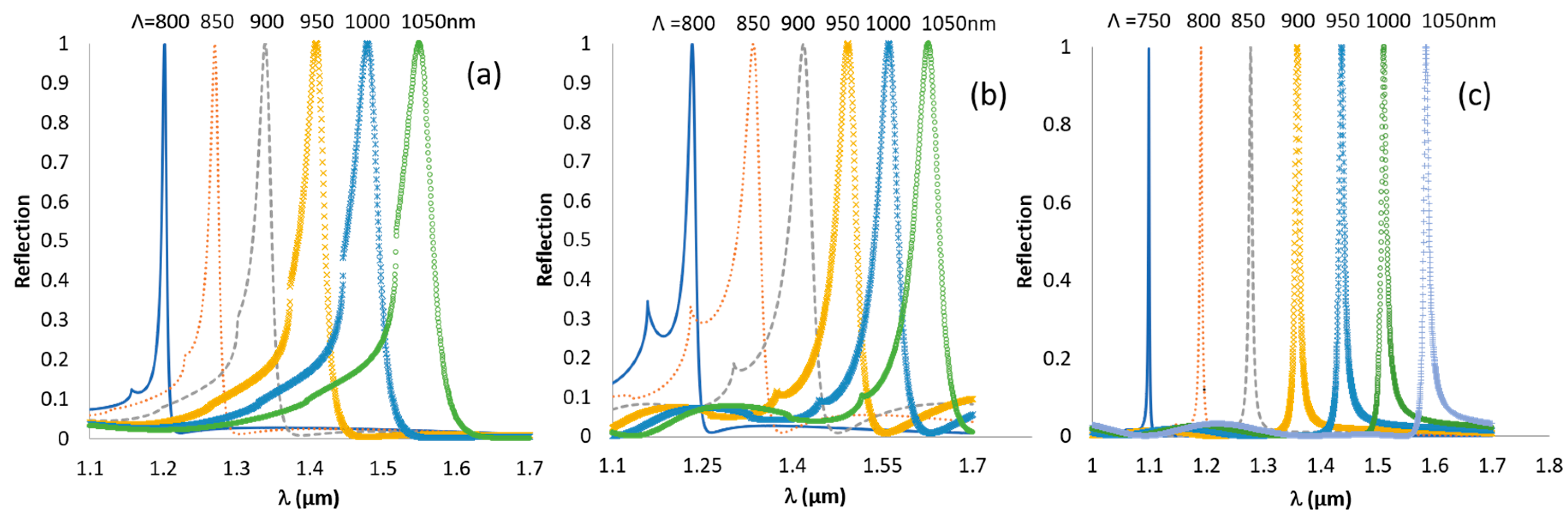
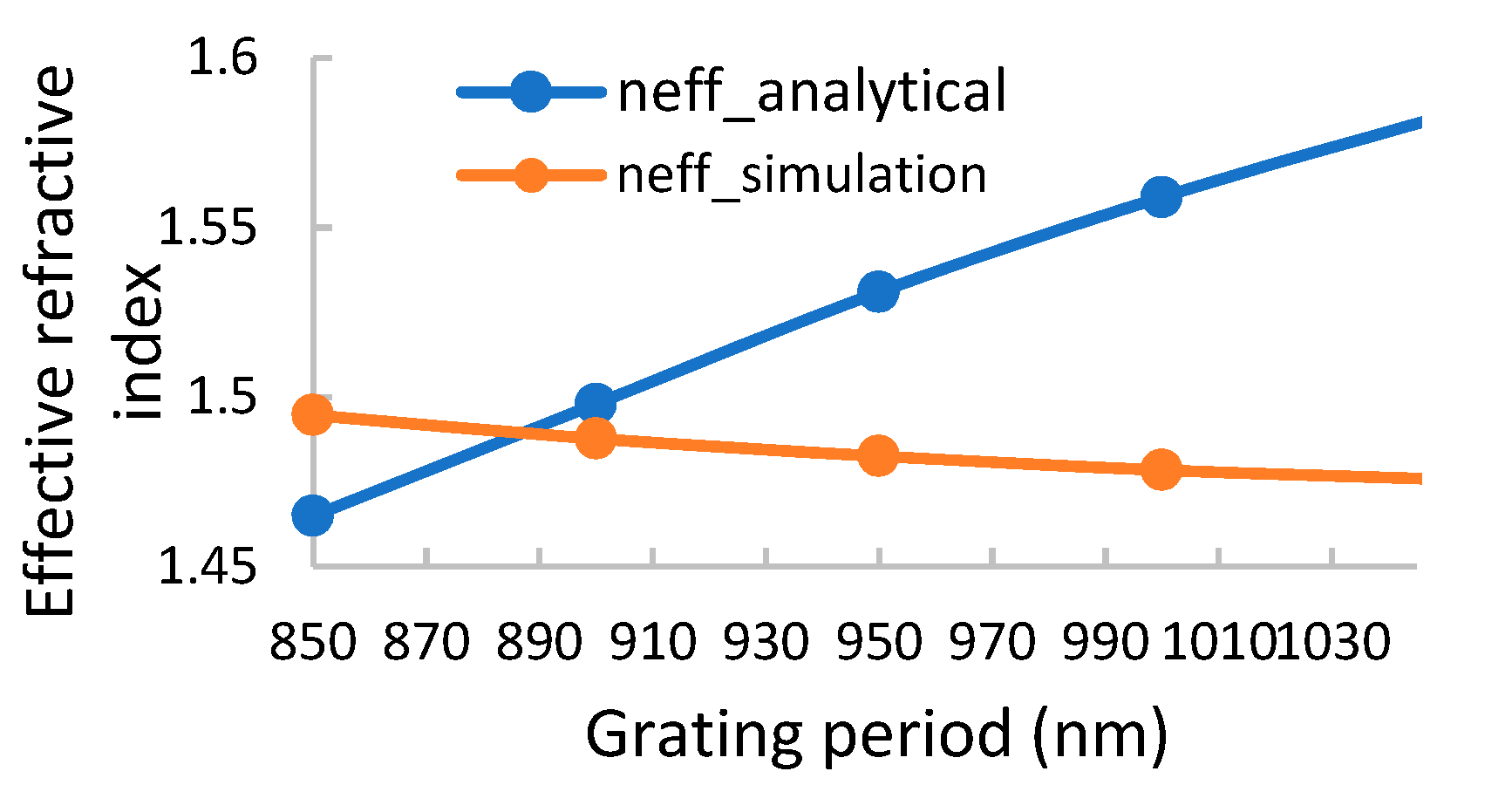
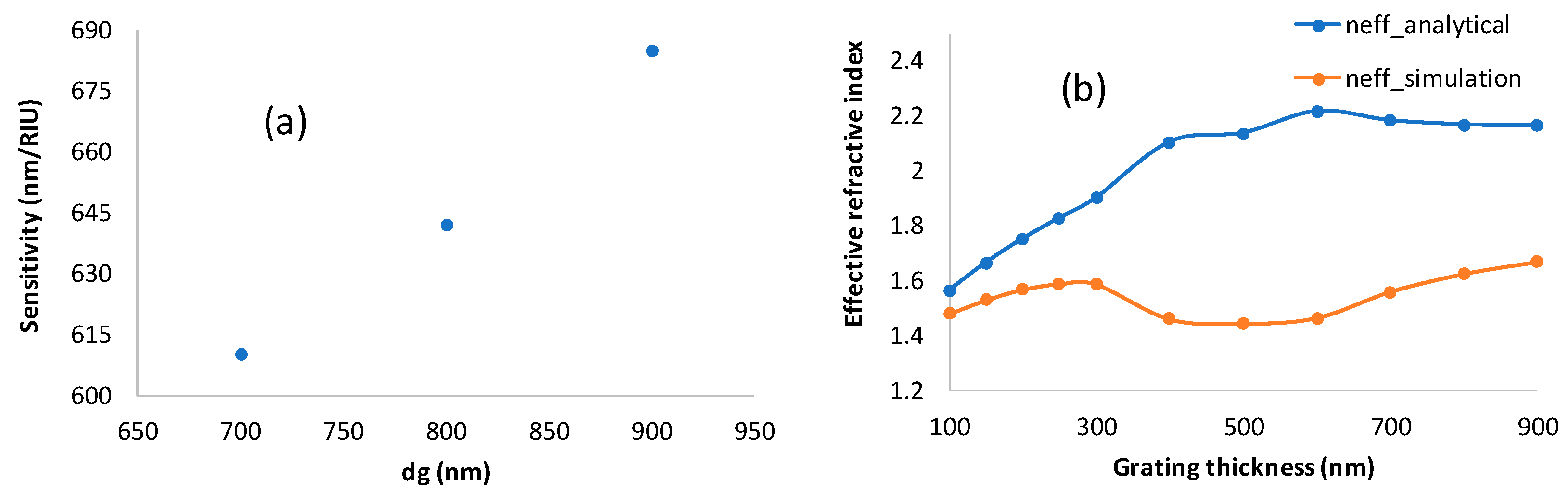
2. Application of the Planar Waveguide Sensor Theory of the Thick Grating GMR
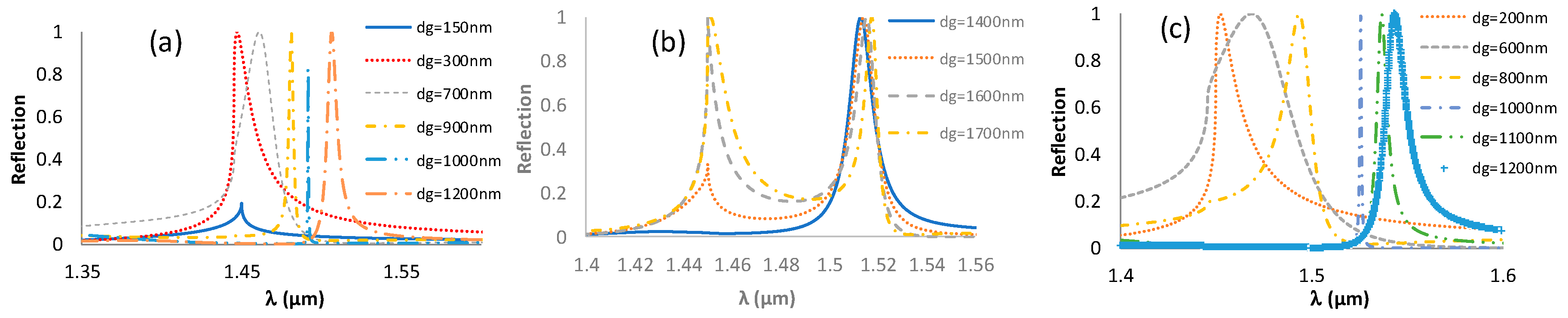
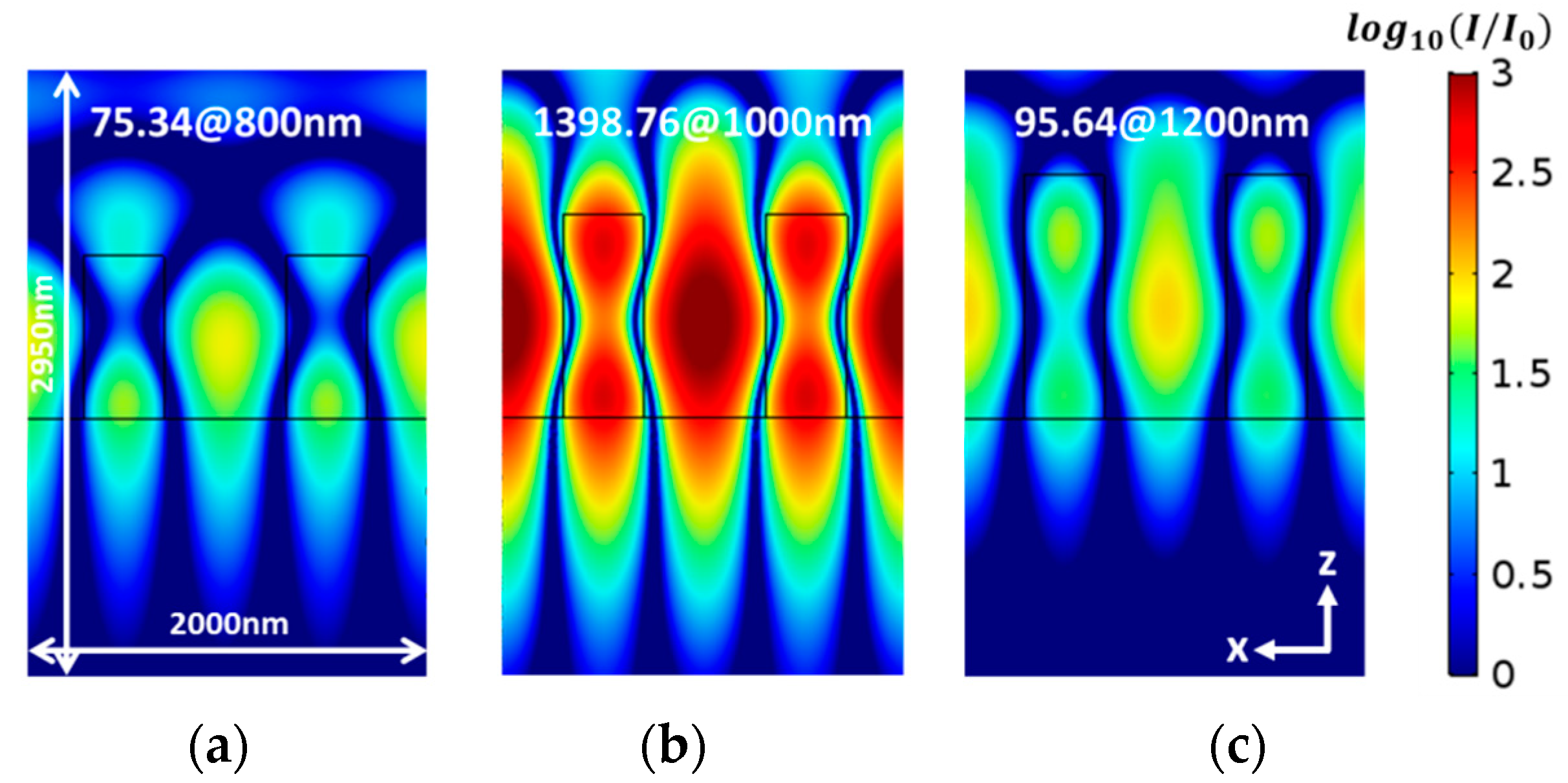
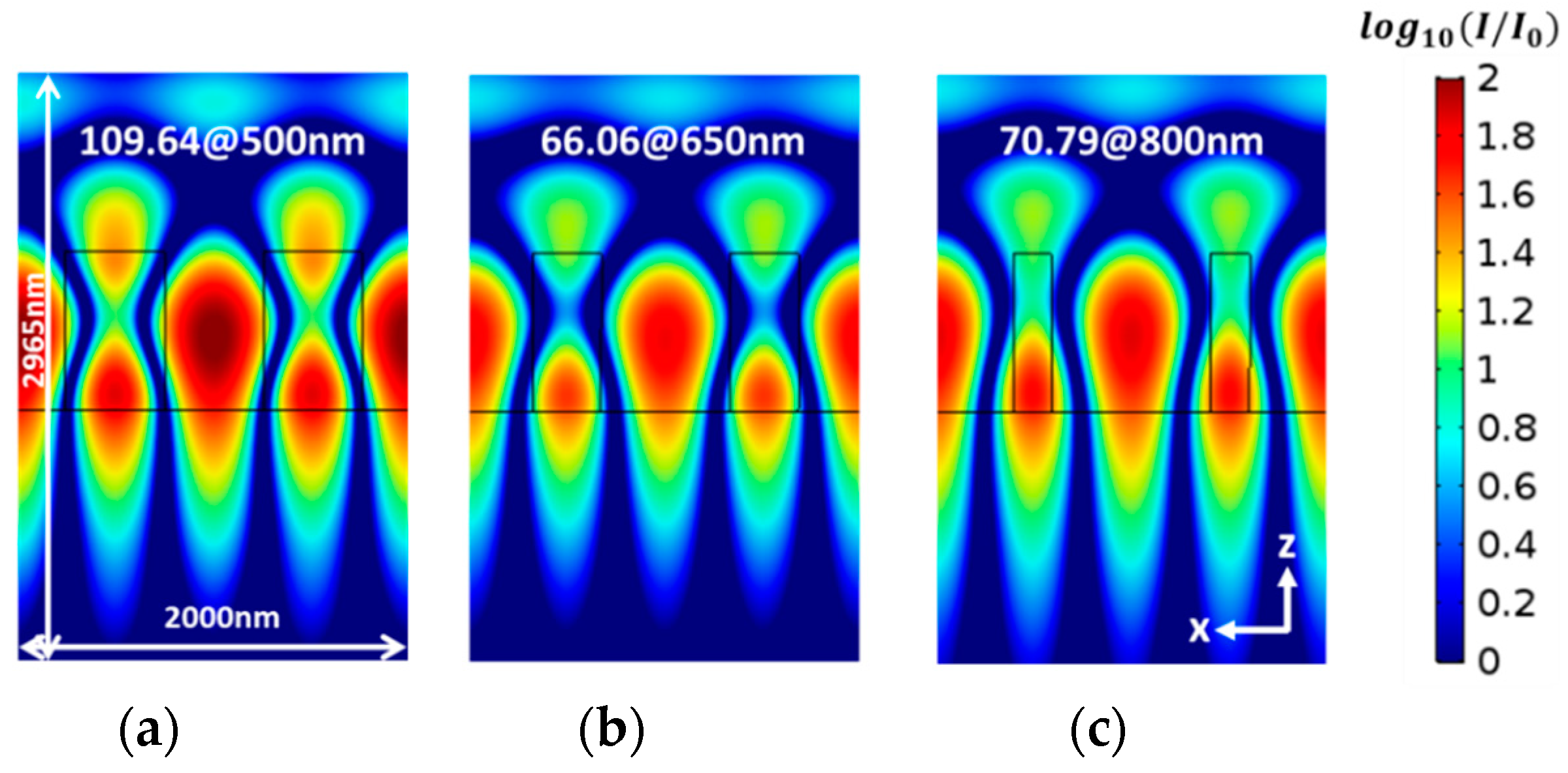
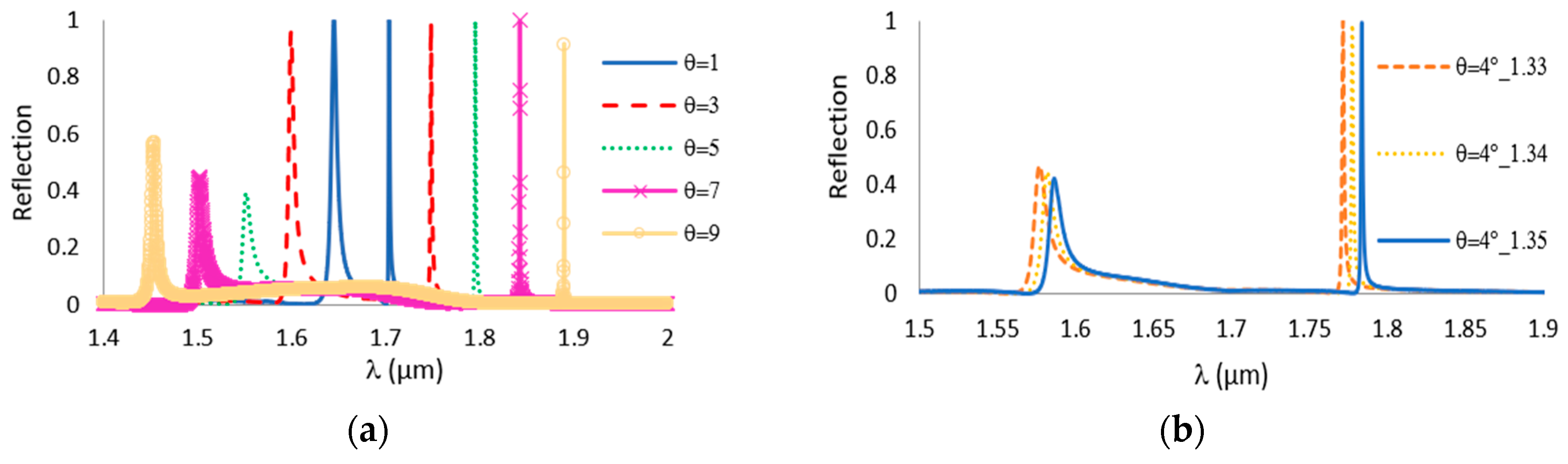
3. Simulation
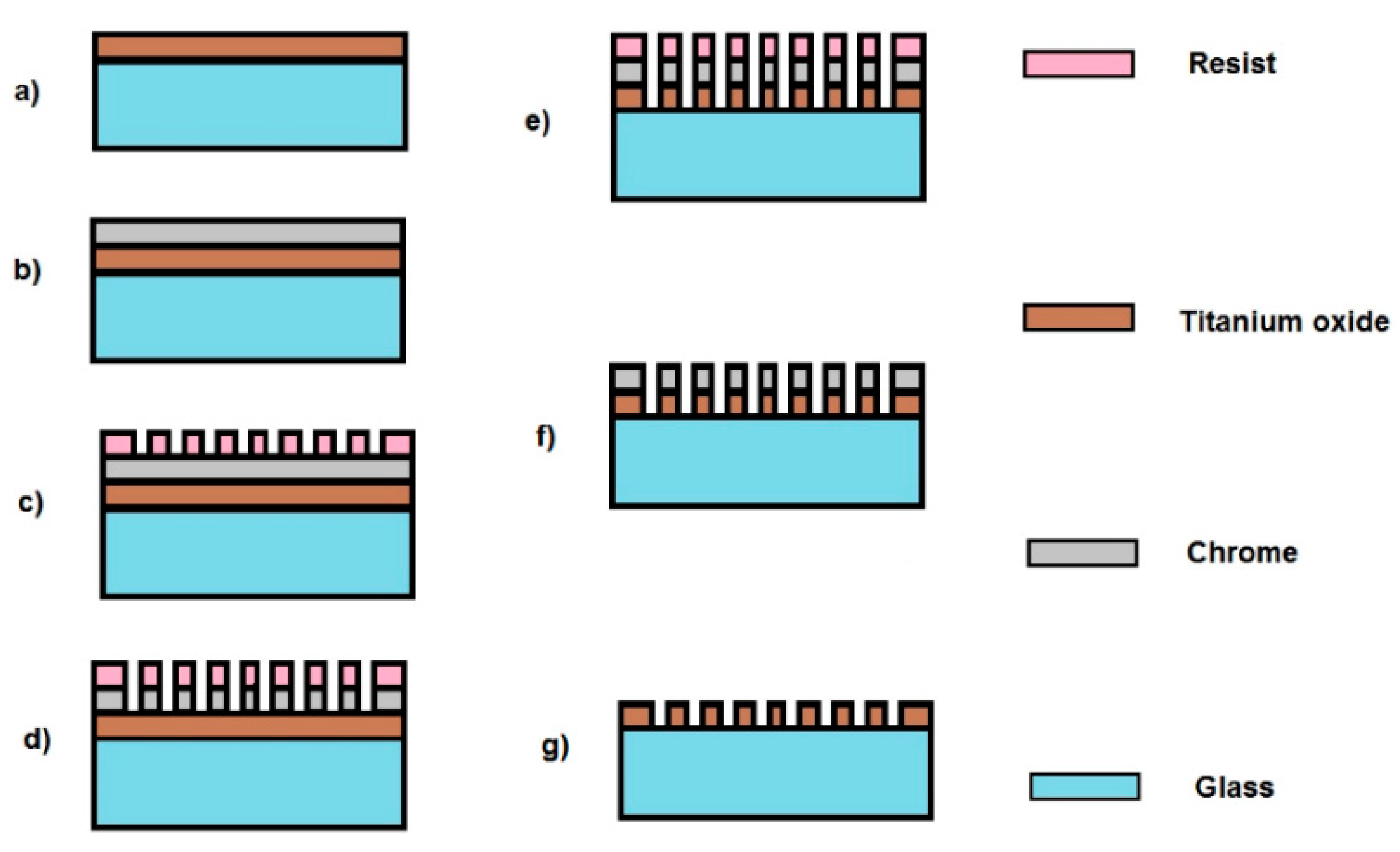
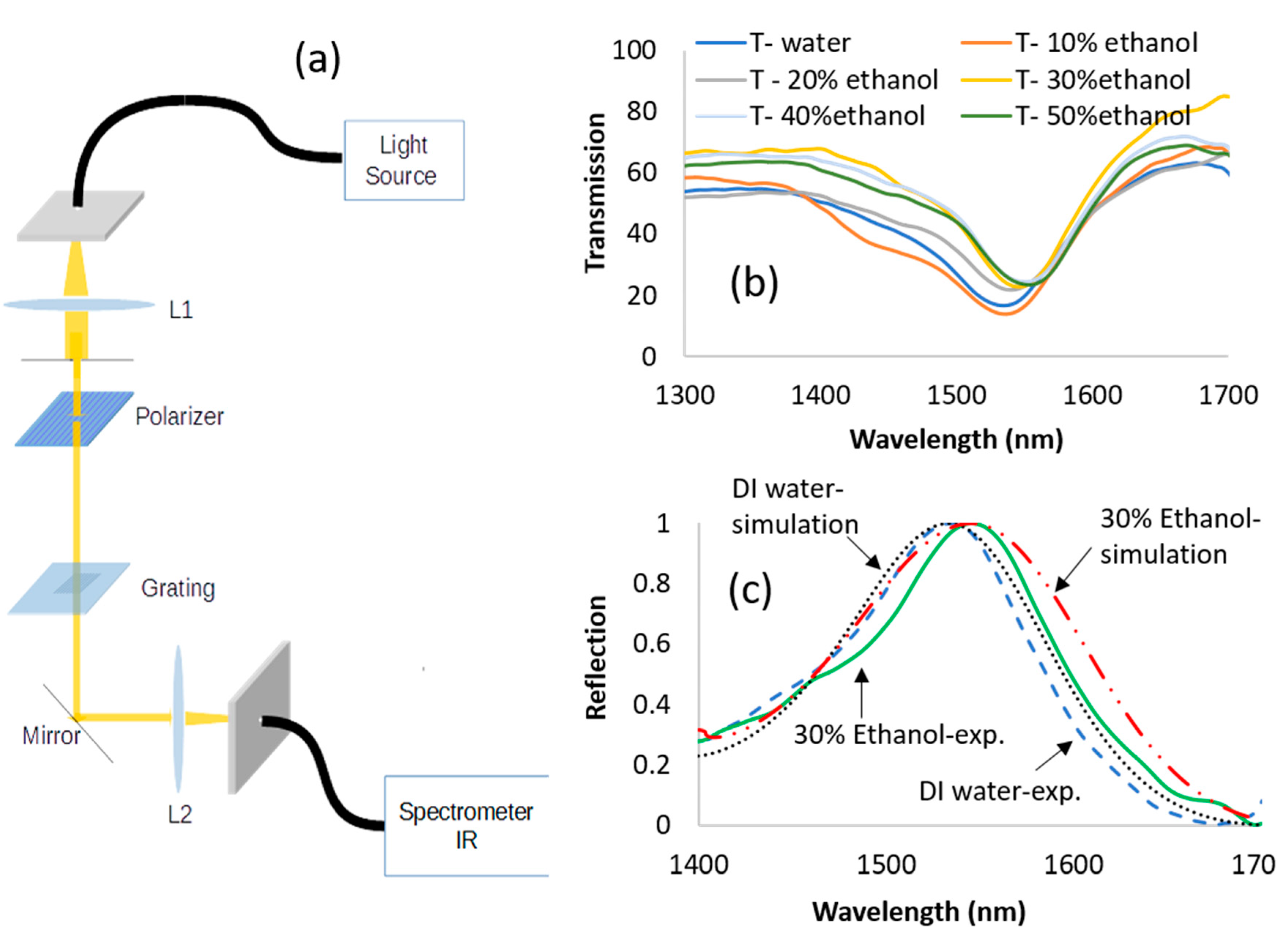
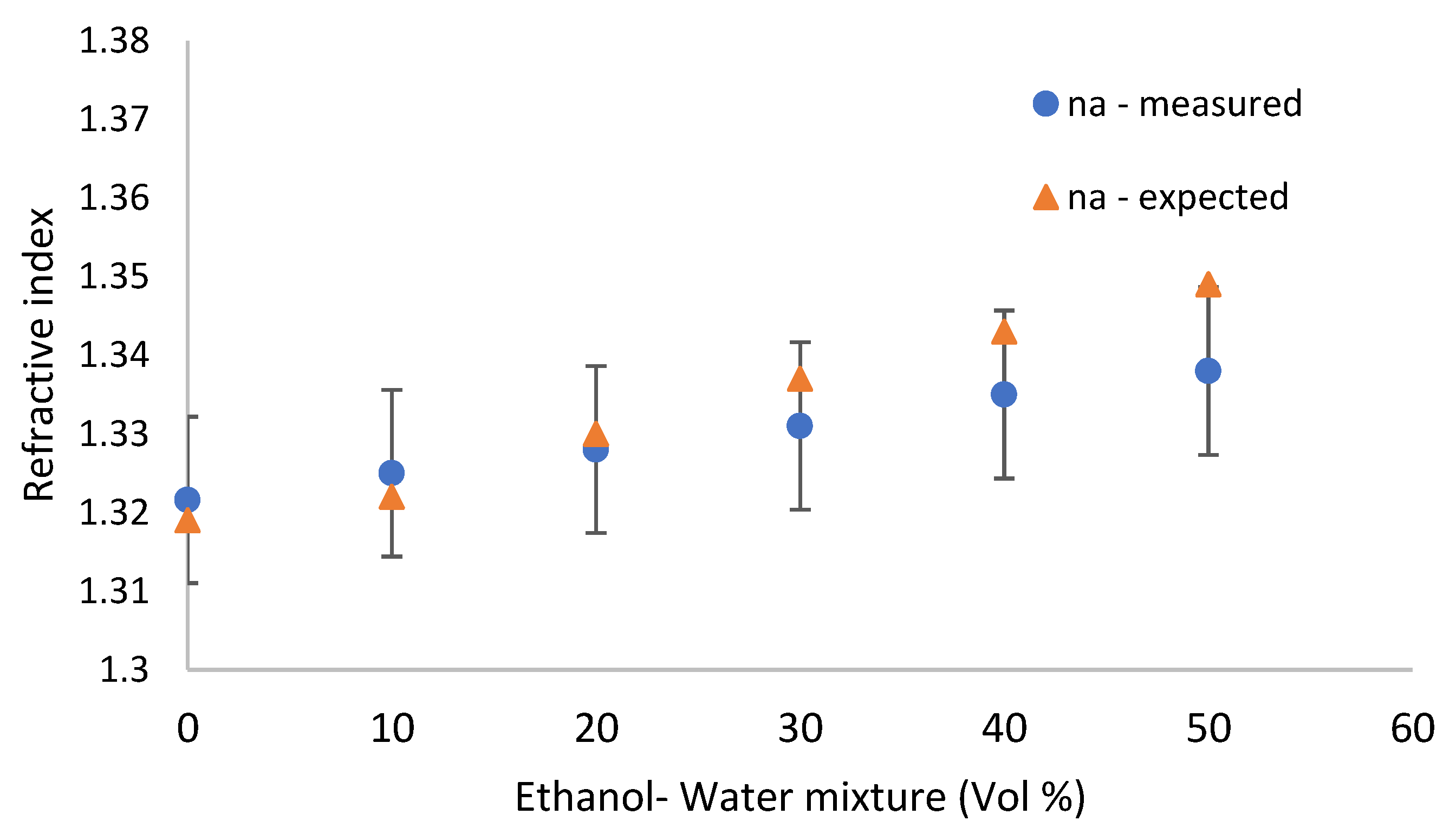
4. Experimental Details and Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wood, R. On a remarkable case of uneven distribution of light in a diffraction grating spectrum. Philos. Mag. 1902, 4, 396–402. [Google Scholar] [CrossRef]
- Lord, R. On the dynamical theory of gratings. Proc. R. Soc. A 1907, 79, 399. [Google Scholar]
- Fano, U. The theory of anomalous diffraction gratings and of quasi-stationary waves on metallic surfaces (Sommerfeld’s waves). J. Opt. Soc. Am. A 1941, 31, 213–222. [Google Scholar] [CrossRef]
- Hessel, A.; Oliner, A.A. A new theory of Wood’s anomalies on optical gratings. Appl. Opt. 1965, 4, 1275. [Google Scholar] [CrossRef]
- Neviere, M. The homogeneous problem. In Electromagnetic Theory of Gratings; Petit, R., Ed.; Springer: Berlin, Germany, 2013; pp. 123–157. [Google Scholar]
- Popov, E.; Mashev, L.; Maystre, D. Theoretical study of anomalies of coated dielectric gratings. Opt. Acta Int. J. Opt. 1986, 32, 607–629. [Google Scholar] [CrossRef]
- Wang, S.S.; Magnusson, R. Theory and applications of guided-mode resonance filters. Appl. Opt. 1993, 32, 2606–2613. [Google Scholar] [CrossRef] [PubMed]
- Pietroy, D.; Tishchenko, A.V.; Flury, M.; Parriaux, O. Bridging pole and coupled wave formalisms for grating waveguide resonance analysis and design synthesis. Opt. Express 2007, 15, 9831–9842. [Google Scholar] [CrossRef]
- Clausnitzer, T.; Tishchenko, A.V.; Kley, E.B.; Fuchs, H.J.; Schelle, D.; Parriaux, O.; Kroll, U. Narrowband, polarization-independent free-space wave notch filter. J. Opt. Soc. Am. A 2005, 22, 2799–2803. [Google Scholar] [CrossRef]
- Destouches, N.; Tishchenko, A.; Pommier, J.; Reynaud, S.; Parriaux, O.; Tonchev, S.; Ahmed, M. 99% efficiency measured in the–1st order of a resonant grating. Opt. Express 2005, 13, 3230–3235. [Google Scholar] [CrossRef]
- Wang, S.S.; Magnusson, R. Multilayer waveguide-grating filters. Appl. Opt. 1995, 34, 2414–2420. [Google Scholar] [CrossRef]
- Magnusson, R.; Wang, S.S. New principle for optical filters. Appl. Phys. Lett. 1992, 61, 1022–1024. [Google Scholar] [CrossRef]
- Klimov, M.S.; Sychugov, V.A.; Tishchenko, A.V.; Parriaux, O. Optimization of optical waveguide grating couplers. Fiber Integ. Opt. 1992, 11, 85–90. [Google Scholar] [CrossRef]
- Kuo, W.K.; Hsu, C.J. Two-dimensional grating guided mode resonance tunable filter. Opt. Express 2017, 25, 29642–29649. [Google Scholar] [CrossRef] [PubMed]
- Sharon, A.; Rosenblatt, D.; Friesem, A.A.; Weber, H.G.; Engel, H.; Steingrueber, R. Light modulation with resonant grating-waveguide structures. Opt. Lett. 1996, 21, 1564–1566. [Google Scholar] [CrossRef] [PubMed]
- Katchalski, T.; Levy-Yurista, G.; Friesem, A.A. Light modulation with electro-optic polymer-based resonant grating waveguide structures. Opt. Express 2005, 13, 4645–4650. [Google Scholar] [CrossRef] [PubMed]
- Abdulhalim, I. Optimized guided mode resonant structure as thermooptic sensor and liquid crystal tunable filter. Chin. Opt. Lett. 2009, 7, 667. [Google Scholar] [CrossRef]
- Cunningham, B.T.; Li, P.; Lin, B.; Pepper, J. Colorimetric resonant reflection as a direct biochemical assay technique. Sens. Actuators B Chem. 2002, 81, 316–328. [Google Scholar] [CrossRef]
- Fang, Y.; Ferries, A.; Fontaine, N.; Mauro, J.; Balakrishnan, J. Resonant waveguide biosensor for living cell sensing. Biophys. J. 2006, 91, 1925–1940. [Google Scholar] [CrossRef]
- Parriaux, O.; Veldhuis, G.J. Normalized analysis for the sensitivity optimization of integrated optical evanescent-wave sensors. J. Lightwave Technol. 1998, 16, 573–582. [Google Scholar] [CrossRef] [Green Version]
- Wawro, D.; Tibuleac, S.; Magnusson, R.; Liu, H. Optical fiber endface biosensor based on resonances in dielectric waveguide gratings. SPIE 2000, 3911, 86–94. [Google Scholar]
- Abdulhalim, I. Biosensing Configurations Using Guided Wave Resonant Structures. In Optical Waveguide Sensing and Imaging; Springer: Dordrecht, The Netherlands, 2008; pp. 211–228. [Google Scholar]
- Sahho, S.P.; Sarkar, S.; Joseph, J. High sensitivity guided mode resonance optical sensor employing phase detection. Sci. Rep. 2017, 7, 7607. [Google Scholar] [CrossRef] [PubMed]
- Boonruang, S.; Mohammed, S.W. Multiwavelength guided mode resonance sensor array. Appl. Phys. Express 2015, 8, 092004. [Google Scholar] [CrossRef]
- Wang, L.; Sang, T.; Li, J.; Zhou, J.; Wang, B.; Wang, Y. High sensitive transmission type of gas sensor based on guided mode resonance in coupled grating. J. Mod. Opt. 2017, 13, 1601–1608. [Google Scholar] [CrossRef]
- Fan, S.; Joannopoulos, J.D. Analysis of guided resonance in photonic crystal slabs. Phys. Rev. B. 2002, 65, 235112. [Google Scholar] [CrossRef]
- Fan, S.H.; Suh, W.; Joannopoulos, J.D. Temporal coupled-mode theory for the Fano resonance in optical resonators. J. Opt. Soc. Am. A 2003, 20, 569–572. [Google Scholar] [CrossRef] [Green Version]
- Chang-Hasnain, C.J.; Yang, W.J. High-contrast gratings for integrated optoelectronics. Adv. Opt. Photonics 2012, 4, 379–440. [Google Scholar] [CrossRef] [Green Version]
- Lalanne, P.; Hugonin, J.P.; Chavel, P. Optical properties of deep lamellar Gratings: A coupled Bloch-mode insight. J. Lightwave Thechnol. 2006, 24, 2442–2449. [Google Scholar] [CrossRef]
- Barillaro, G.; Merlo, S.; Surdo, S.; Strambini, L.M.; Carpignano, F. Integrated optofluidic microsystem based on vertical high-order one-dimensional silicon photonic crystals. Microfluid. Nanofluidic. 2012, 12, 545–552. [Google Scholar] [CrossRef]
- Peters, D.W.; Kemme, S.A.; Hadley, G.R. Effect of finite grating, waveguide width, and end-facet geometry on resonant subwavelength grating reflectivity. J. Opt. Soc. Am. A 2004, 21, 981–987. [Google Scholar] [CrossRef]
- Krasnykov, O.; Auslander, M.; Abdulhalim, I. Optimizing the guided mode resonance structure for optical sensing in water. Phys. Express 2011, 1, 183–190. [Google Scholar]
- Kozmaa, P.; Kehlb, F.; Ehrentreich-Förstera, E.; Stamm, C. Integrated planar optical waveguide interferometer biosensors: A comparative review. Biosens. Bioelectron. 2014, 58, 287–307. [Google Scholar] [CrossRef] [PubMed]
- Tiefenthaler, K.; Lukosz, W. Sensitivity of grating couplers as integrated-optical chemical sensors. J. Opt. Soc. Am. B 1989, 6, 209–220. [Google Scholar] [CrossRef]
- Abdulhalim, I. Simplified optical scatterometry for periodic nanoarrays in the near-quasi-static limit. Appl. Opt. 2007, 46, 2219–2228. [Google Scholar] [CrossRef] [PubMed]
- GSolver Rigorous Diffraction Grating Analysis. Available online: http://www.gsolver.com (accessed on 6 July 2019).
- Day, W.R.; Wang, S.S.; Magnusson, R. Filter response line shapes of resonant waveguide gratings. J. Lightwawe Technol. 1996, 14, 1815–1824. [Google Scholar] [CrossRef]
- Vadim, K.; Connie, J.C.H. Physics of near-wavelength high contrat gratings. Opt. Express 2012, 20, 10889–10895. [Google Scholar]
- Lalanne, P.; Lamercier-Lalanne, D. Depth dependence of the effective properties of subwavelength gratings. J. Opt. Soc. Am. A 1997, 14, 450–458. [Google Scholar] [CrossRef]
- Kikuta, H.; Maegawa, N.; Mizutani, A.; Iwata, K.; Toyota, H. Refractive index sensor with a guided-mode resonant grating filter. SPIE 2001, 4416, 219–222. [Google Scholar]
- Wangüemert-Pérez, J.G.; Cheben, P.; Moñux, A.O.; Ramos, C.A.; Pérez-Galacho, D.; Halir, R.; Molina-Fernández, I.; Xu, D.X.; Schmid, J.H. Evanescent field waveguide sensing with subwavelength grating structures in silicon-on-insulator. Opt. Lett. 2014, 39, 4442–4445. [Google Scholar] [CrossRef] [PubMed]
- Lue, J.H.; Ding, T.J.; Chang, R.S. Waveguide thickness effects on the sensitivity of Lamellar grating waveguide sensor with TE polarization incidence. Life Sci. J. 2014, 11, 394–397. [Google Scholar]
- van, H.L.; Buczynski, R.; Long, V.C.; Trippenbach, M.; Borzycki, K.; Manh, A.N.; Kasztetelanic, R. Measurement of temperature and concentration influence on the dispersion of fused silica glass photonic crystal fiber infiltrated with water–ethanol mixture. Opt. Commun. 2018, 407, 417–422. [Google Scholar] [CrossRef]
- Sun, T.; Kan, S.; Marriott, G.; Hasnain, C.C. High contrant grating sensor for label free detection of disease biomarkers. Sci. Rep. 2016, 6, 27482. [Google Scholar] [CrossRef] [PubMed]
- Reis, J.C.; Lampreia, I.M.; Santos, A.F.; Moita, M.L.; Douheret, G. Refractive index of liquid mixtures: Theory and experiment. Chem. Phys. Chem. 2011, 11, 3722. [Google Scholar] [CrossRef] [PubMed]
- Photonicsys. Available online: www.photonicsys.com (accessed on 6 July 2019).
- Abutoama, M.; Li, S.; Abdulhalim, I. Widening the spectral range of ultrahigh field enhancement by efficient coupling of localized to extended plasmons and cavity resonances in grating geometry. J. Phys. Chem. C 2017, 121, 27612–27623. [Google Scholar] [CrossRef]
- Abdulhalim, I. Coupling configurations between extended surface electromagnetic waves and localized surface plasmons for ultrahigh field enhancement. Nanophotonics 2018, 7, 1891–1916. [Google Scholar] [CrossRef]
- Isaacs, S.; Harté, E.; Alves, I.D.; Abdulhalim, I. Improved detection of plasmon waveguide resonance using diverging beam, liquid crystal retarder, and application to lipid orientation determination. Sensors 2019, 19, 1402. [Google Scholar] [CrossRef] [PubMed]
- Abdulhalim, I.; Auslender, M.; Hava, S. Resonant and scatterometric gratings based nano-photonic structures for biosensing. J. Nanophotonics 2007, 1, 011680. [Google Scholar]




| Property | GMR without a Planar Waveguide | GMR with a Planar Waveguide |
|---|---|---|
| Location of the resonance as a function of grating thickness | As the thickness of the grating increase the resonance shifts to longer wavelength. | |
| Location of the resonance as a function of grating period | As the period increases the resonance shifts the longer wavelength. | |
| FWHM as a function of polarization | For TM the FWHM is smaller | |
| Typical sensitivity in the angular configuration | 70°/deg | 35.8°/deg [40] |
| Sensitivity as a function of fill factor (f) | For f between 0.25–0.5 the sensitivity is maximum. | As the f increase the sensitivity decreases. [41] |
| Sensitivity as a function of thickness | As the thickness of the grating increases, the sensitivity increases. | As the thickness of the waveguide increases the sensitivity decreases. [42] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isaacs, S.; Hajoj, A.; Abutoama, M.; Kozlovsky, A.; Golan, E.; Abdulhalim, I. Resonant Grating without a Planar Waveguide Layer as a Refractive Index Sensor. Sensors 2019, 19, 3003. https://doi.org/10.3390/s19133003
Isaacs S, Hajoj A, Abutoama M, Kozlovsky A, Golan E, Abdulhalim I. Resonant Grating without a Planar Waveguide Layer as a Refractive Index Sensor. Sensors. 2019; 19(13):3003. https://doi.org/10.3390/s19133003
Chicago/Turabian StyleIsaacs, Sivan, Ansar Hajoj, Mohammad Abutoama, Alexander Kozlovsky, Erez Golan, and Ibrahim Abdulhalim. 2019. "Resonant Grating without a Planar Waveguide Layer as a Refractive Index Sensor" Sensors 19, no. 13: 3003. https://doi.org/10.3390/s19133003
APA StyleIsaacs, S., Hajoj, A., Abutoama, M., Kozlovsky, A., Golan, E., & Abdulhalim, I. (2019). Resonant Grating without a Planar Waveguide Layer as a Refractive Index Sensor. Sensors, 19(13), 3003. https://doi.org/10.3390/s19133003






