A Novel Chiller Sensors Fault Diagnosis Method Based on Virtual Sensors
Abstract
1. Introduction
- In order to ensure the performance of virtual sensors, MIC is used to examine potentially interesting relationships between sensors. Chiller sensors with high MIC scores are divided into the same groups. This could dramatically improve the fitting effect of virtual sensors by constructing them in the same group.
- The performance of virtual sensors could be easily impacted by the input sensors. In order to reduce the false alarm rate, two virtual sensors that have different input sensors are constructed for the same physical sensor. When the two deviations between the corresponding physical sensor and the two virtual sensors both exceed the thresholds, the physical sensor is considered as a fault state.
- The LSTM model, which can better extract discriminating features from the sensor data, is used to construct the virtual sensors. It could further improve the fitting effect of virtual sensors.
2. Coupling Characteristic Analysis of the Air-Cooled Chiller System
3. Methods
3.1. Maximal Information Coefficient
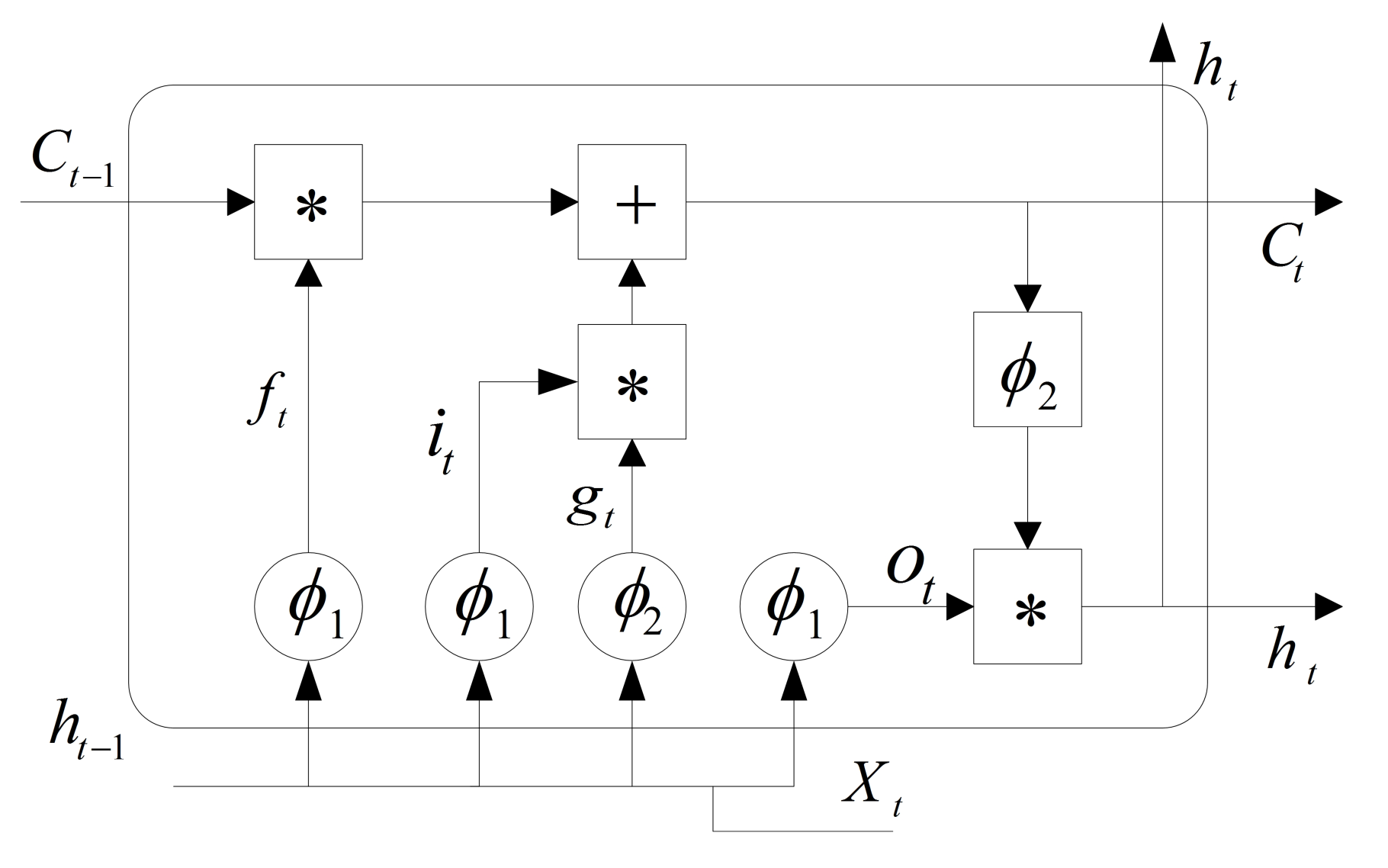
3.2. Virtual Sensors
3.3. The Threshold and Procedure of Fault Diagnosis
- Step 1:
- A physical sensor is selected from eleven sensors. Two virtual sensors, which have been constructed in the training period, are used to predict the value of this physical sensor.
- Step 2:
- Deviations between virtual and physical sensors are calculated and compared with the fault diagnosis threshold.
- Step 3:
- Obviously, the physical sensor is not considered as a fault state when no deviations exceed the threshold. On the contrary, a sensor fault occurs when the deviations both exceed the fault diagnosis threshold. Input sensors are considered as a fault state if only one absolute deviation exceeds the threshold, because two virtual sensors have different input sensors. Under this situation, another physical sensor from input sensors is selected and step 2 will be repeated to predict the value of another physical sensor.
4. Results and Discussion
4.1. Experimental Data
4.2. Performance Comparison
4.2.1. Verification of Low False Alarm Rate
4.2.2. Fault Diagnosis Performance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brambley, M. Review article: Methods for fault detection, diagnostics, and prognostics for building systems—A review, Part II. HVAC R Res. 2005, 11, 19. [Google Scholar]
- Zheng, Y.; Ghahramani, A.; Becerik-Gerber, B. Building occupancy diversity and HVAC (heating, ventilation, and air conditioning) system energy efficiency. Energy 2016, 109, 641–649. [Google Scholar]
- Saidur, R.; Hasanuzzaman, M.; Mahlia, T.M.I.; Rahim, N.A.; Mohammed, H.A. Chillers energy consumption, energy savings and emission analysis in an institutional buildings. Energy 2011, 36, 5233–5238. [Google Scholar] [CrossRef]
- Katipamula, S.; Brambley, M. Review article: Methods for fault detection, diagnostics, and prognostics for building systems—A review, Part I. Hvac R Res. 2005, 11, 3–25. [Google Scholar] [CrossRef]
- Li, Z.; Li, Q.; Wu, Z.; Jie, Y.; Zheng, R. A fault diagnosis method for on load tap changer of aerospace power grid based on the current detection. IEEE Access 2018, 6, 1. [Google Scholar] [CrossRef]
- Ma, J.; Jin, J. Applications of fault detection and diagnosis methods in nuclear power plants: A review. Prog. Nucl. Energy 2011, 53, 255–266. [Google Scholar] [CrossRef]
- Chi, M.V.; Wong, P.K.; Wong, K.I. Simultaneous-fault detection based on qualitative symptom descriptions for automotive engine diagnosis. Appl. Soft Comput. 2014, 22, 238–248. [Google Scholar]
- Dinca, L.; Aldemir, T.; Rizzoni, G. A model-based probabilistic approach for fault detection and identification with application to the diagnosis of automotive engines. IEEE Trans. Autom. Control 2002, 44, 2200–2205. [Google Scholar] [CrossRef]
- Kim, W.; Katipamula, S. A review of fault detection and diagnostics methods for building systems. Sci. Technol. Built Environ. 2017, 24, 3–21. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part II: Fault diagnosis with knowledge-based and hybrid/active approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar] [CrossRef]
- Ren, N. PCA-SVM-based automated fault detection and diagnosis (AFDD) for vapor-compression refrigeration systems. Hvac R Res. 2010, 16, 295–313. [Google Scholar]
- Li, D.; Li, D.; Li, C.; Li, L.; Gao, L. A novel data-temporal attention network based strategy for fault diagnosis of chiller sensors. Energy Build. 2019, 198, 377–394. [Google Scholar] [CrossRef]
- Bo, F.; Du, Z.; Jin, X.; Yang, X.; Guo, Y. A hybrid FDD strategy for local system of AHU based on artificial neural network and wavelet analysis. Build. Environ. 2010, 45, 2698–2708. [Google Scholar]
- Benmoussa, S.; Djeziri, M.A. Remaining useful life estimation without needing for prior knowledge of the degradation features. IET Sci. Meas. Technol. 2017, 11, 1071–1078. [Google Scholar] [CrossRef]
- Ms, L.H.C.; Russell, E.L.; Braatz, R.D. Fault Detection and Diagnosis in Industrial Systems; Springer: London, UK, 2001. [Google Scholar]
- Yu, Y.; Woradechjumroen, D.; Yu, D. A review of fault detection and diagnosis methodologies on air-handling units. Energy Build. 2014, 82, 550–562. [Google Scholar] [CrossRef]
- Mattera, C.G.; Quevedo, J.; Escobet, T.; Shaker, H.R.; Jradi, M. A method for fault detection and diagnostics in ventilation units using virtual sensors. Sensors 2018, 18, 3931. [Google Scholar] [CrossRef]
- Ergan, S.; Radwan, A.; Zou, Z.; Tseng, H.A.; Han, X. Quantifying human experience in architectural spaces with integrated virtual reality and body sensor networks. J. Comput. Civ. Eng. 2018, 33, 04018062. [Google Scholar] [CrossRef]
- Tegen, A.; Davidsson, P.; Mihailescu, R.C.; Persson, J. Collaborative sensing with interactive learning using dynamic intelligent virtual sensors. Sensors 2019, 19, 477. [Google Scholar] [CrossRef]
- Wei, C.; Chen, J.; Song, Z.; Chen, C.I. Adaptive virtual sensors using SNPER for the localized construction and elastic net regularization in nonlinear processes. Control Eng. Pract. 2019, 83, 129–140. [Google Scholar] [CrossRef]
- Valdivia, C.G.; Escobedo, J.L.C.; Durán-Muñoz, H.A.; Berumen, J.; Hernandez-Ortiz, M. Implementation of virtual sensors for monitoring temperature in greenhouses using CFD and control. Sensors 2019, 19, 60. [Google Scholar]
- Yoon, S.; Yu, Y. Strategies for virtual in-situ sensor calibration in building energy systems. Energy Build. 2018, 172, 22–34. [Google Scholar] [CrossRef]
- Li, H.; Yu, D.; Braun, J. A review of virtual sensing technology and application in building systems. Hvac R Res. 2011, 17, 619–645. [Google Scholar]
- Mattera, C.G.; Quevedo, J.; Escobet, T.; Shaker, H.R.; Jradi, M. Fault detection and diagnostics in ventilation units using linear regression virtual sensors. In Proceedings of the International Symposium on Advanced Electrical and Communication Technologies (ISAECT), Rabat, Morocco, 21–23 November 2018. [Google Scholar]
- Reppa, V.; Papadopoulos, P.; Polycarpou, M.M.; Panayiotou, C.G. A distributed virtual sensor scheme for smart buildings based on adaptive approximation. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 99–106. [Google Scholar]
- Kusiak, A.; Li, M.; Zheng, H. Virtual models of indoor-air-quality sensors. Appl. Energy 2010, 87, 2087–2094. [Google Scholar] [CrossRef]
- Kanjo, E.; Younis, E.; Ang, C.S. Deep learning analysis of mobile physiological, environmental and location sensor data for emotion detection. Inf. Fusion 2018, 49, 46–56. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Shin, H.; Roth, H.R.; Gao, M.; Lu, L.; Xu, Z.; Nogues, I.; Yao, J.; Mollura, D.; Summers, R.M. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar] [CrossRef] [PubMed]
- Vinh, N.X.; Epps, J.; Bailey, J. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. J. Mach. Learn. Res. 2010, 11, 2837–2854. [Google Scholar]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; Gilean, M.V.; Turnbaugh, P.J.; Lander, E.S.; Michael, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef]








| No. | Sensors | Descriptions | Unit |
|---|---|---|---|
| 1 | Compressor suction temperature | C | |
| 2 | Compressor discharge temperature | C | |
| 3 | Condenser-air temperature at the outlet | C | |
| 4 | Refrigerant temperature before throttling | C | |
| 5 | Refrigerant temperature after throttling | C | |
| 6 | Chilled-water supply temperature | C | |
| 7 | Chilled-water return temperature | C | |
| 8 | Compressor suction pressure | MPa | |
| 9 | Compressor discharge pressure | MPa | |
| 10 | Inlet pressure of the throttle device | MPa | |
| 11 | Outlet pressure of the throttle device | MPa |
| 1 | 0.239 | 0.264 | 0.279 | 0.432 | 0.850 | 0.881 | 0.267 | 0.271 | 0.618 | 0.832 | |
| 0.239 | 1 | 0.812 | 0.652 | 0.307 | 0.237 | 0.237 | 0.750 | 0.827 | 0.319 | 0.092 | |
| 0.264 | 0.812 | 1 | 0.836 | 0.249 | 0.305 | 0.299 | 0.922 | 0.898 | 0.255 | 0.160 | |
| 0.279 | 0.652 | 0.836 | 1 | 0.289 | 0.337 | 0.328 | 0.864 | 0.906 | 0.273 | 0.188 | |
| 0.432 | 0.307 | 0.249 | 0.289 | 1 | 0.348 | 0.422 | 0.255 | 0.263 | 0.906 | 0.805 | |
| 0.850 | 0.237 | 0.305 | 0.337 | 0.348 | 1 | 0.886 | 0.334 | 0.333 | 0.335 | 0.516 | |
| 0.881 | 0.237 | 0.299 | 0.328 | 0.422 | 0.886 | 1 | 0.325 | 0.328 | 0.431 | 0.499 | |
| 0.267 | 0.750 | 0.922 | 0.864 | 0.255 | 0.334 | 0.325 | 1 | 0.940 | 0.260 | 0.180 | |
| 0.271 | 0.827 | 0.898 | 0.906 | 0.263 | 0.333 | 0.328 | 0.940 | 1 | 0.262 | 0.183 | |
| 0.618 | 0.319 | 0.255 | 0.273 | 0.906 | 0.335 | 0.431 | 0.260 | 0.262 | 1 | 0.135 | |
| 0.832 | 0.092 | 0.160 | 0.188 | 0.805 | 0.516 | 0.499 | 0.180 | 0.183 | 0.135 | 1 |
| Grouping Threshold | Group |
|---|---|
| 0.8 | {, , , } {, , , } |
| 0.6 | {, , , , } {, , , , } |
| 0.3 | {, , , , , } {, , , , , , } |
| Sensors | Unit | Biases |
|---|---|---|
| C | ±0.5, ±0.65, ±0.8, ±0.95 | |
| C | ±1.5, ±1.9, ±2.3, ±2.7 | |
| C | ±1.0, ±1.3, ±1.6, ±1.9 | |
| C | ±1.0, ±1.3, ±1.6, ±1.9 | |
| C | ±0.4, ±0.5, ±0.6, ±0.7 | |
| C | ±0.4, ±0.5, ±0.6, ±0.7 | |
| C | ±0.4, ±0.5, ±0.6, ±0.7 | |
| MPa | ±0.035, ±0.04, ±0.045, ±0.05 | |
| MPa | ±0.07, ±0.08, ±0.09, ±0.10 | |
| MPa | ±0.07, ±0.08, ±0.09, ±0.10 | |
| MPa | ±0.035, ±0.04, ±0.045, ±0.05 |
| Only one virtual sensor | 35.0% | 18.0% | 26.0% | 52.0% | 44.0% | 27.0% | 39.0% | 11.0% | 23.0% | |
| Two virtual sensors | 0.00% | 3.0% | 0.00% | 0.00% | 0.00% | 2.0% | 4.0% | 0.00% | 0.00% |
| LR-based, LSTM-based | |||||||||
| FC-based, LSTM-based |
| LR-based | 1.37 | 0.89 | 0.87 | 0.42 | 0.44 | 0.38 | 0.061 | 0.057 | 0.032 | |
| Positive | FC-based | 1.08 | 0.84 | 0.85 | 0.29 | 0.21 | 0.27 | 0.049 | 0.053 | 0.021 |
| LSTM-based | 0.85 | 0.68 | 0.69 | 0.17 | 0.19 | 0.20 | 0.034 | 0.038 | 0.016 | |
| LR-based | 1.41 | 0.82 | 0.89 | 0.33 | 0.47 | 0.39 | 0.067 | 0.062 | 0.035 | |
| Negative | FC-based | 1.12 | 0.89 | 0.81 | 0.33 | 0.27 | 0.31 | 0.052 | 0.058 | 0.018 |
| LSTM-based | 0.87 | 0.56 | 0.75 | 0.20 | 0.21 | 0.25 | 0.032 | 0.040 | 0.019 |
| LR-based | 90.5% | 92.25% | 91.0% | 94.5% | 93.25% | 89.5% | 90.5% | 92.5% | 93.0% | 95.25% | 94.5% |
| FC-based | 93.75% | 93.5% | 96.25% | 95.75% | 95.5% | 91.75% | 97.5% | 96.0% | 95.5% | 96.25% | 97.75% |
| LSTM-based | 98% | 98.5% | 98.75% | 97.25% | 97.75% | 96.25% | 100.0% | 97.25% | 99.25% | 97.5% | 99.5% |
| LR-based | 90.25% | 92.5% | 89.25% | 94.25% | 92.5% | 86.5% | 86.25% | 89.75% | 94.5% | 95.0% | 94.25% | |
| FC-based | 91.25% | 96.75% | 92.25% | 96.0% | 95.5% | 92.25% | 93.5% | 94.0% | 96.75% | 97.5% | 96.75% | |
| LSTM-based | 95.25% | 98.75% | 93.0% | 95.5% | 97.5% | 96.75% | 95.25% | 98.5% | 98.5% | 99.25% | 97.25% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Li, D.; Li, D.; Yao, L.; Liang, L.; Gao, Y. A Novel Chiller Sensors Fault Diagnosis Method Based on Virtual Sensors. Sensors 2019, 19, 3013. https://doi.org/10.3390/s19133013
Gao L, Li D, Li D, Yao L, Liang L, Gao Y. A Novel Chiller Sensors Fault Diagnosis Method Based on Virtual Sensors. Sensors. 2019; 19(13):3013. https://doi.org/10.3390/s19133013
Chicago/Turabian StyleGao, Long, Donghui Li, Ding Li, Lele Yao, Limei Liang, and Yanan Gao. 2019. "A Novel Chiller Sensors Fault Diagnosis Method Based on Virtual Sensors" Sensors 19, no. 13: 3013. https://doi.org/10.3390/s19133013
APA StyleGao, L., Li, D., Li, D., Yao, L., Liang, L., & Gao, Y. (2019). A Novel Chiller Sensors Fault Diagnosis Method Based on Virtual Sensors. Sensors, 19(13), 3013. https://doi.org/10.3390/s19133013





