Measurements of Normal Incidence Reflection Loss as a Function of Temperature at the Water-Castor Oil Interface †
Abstract
:1. Introduction
2. Acoustic Measurements
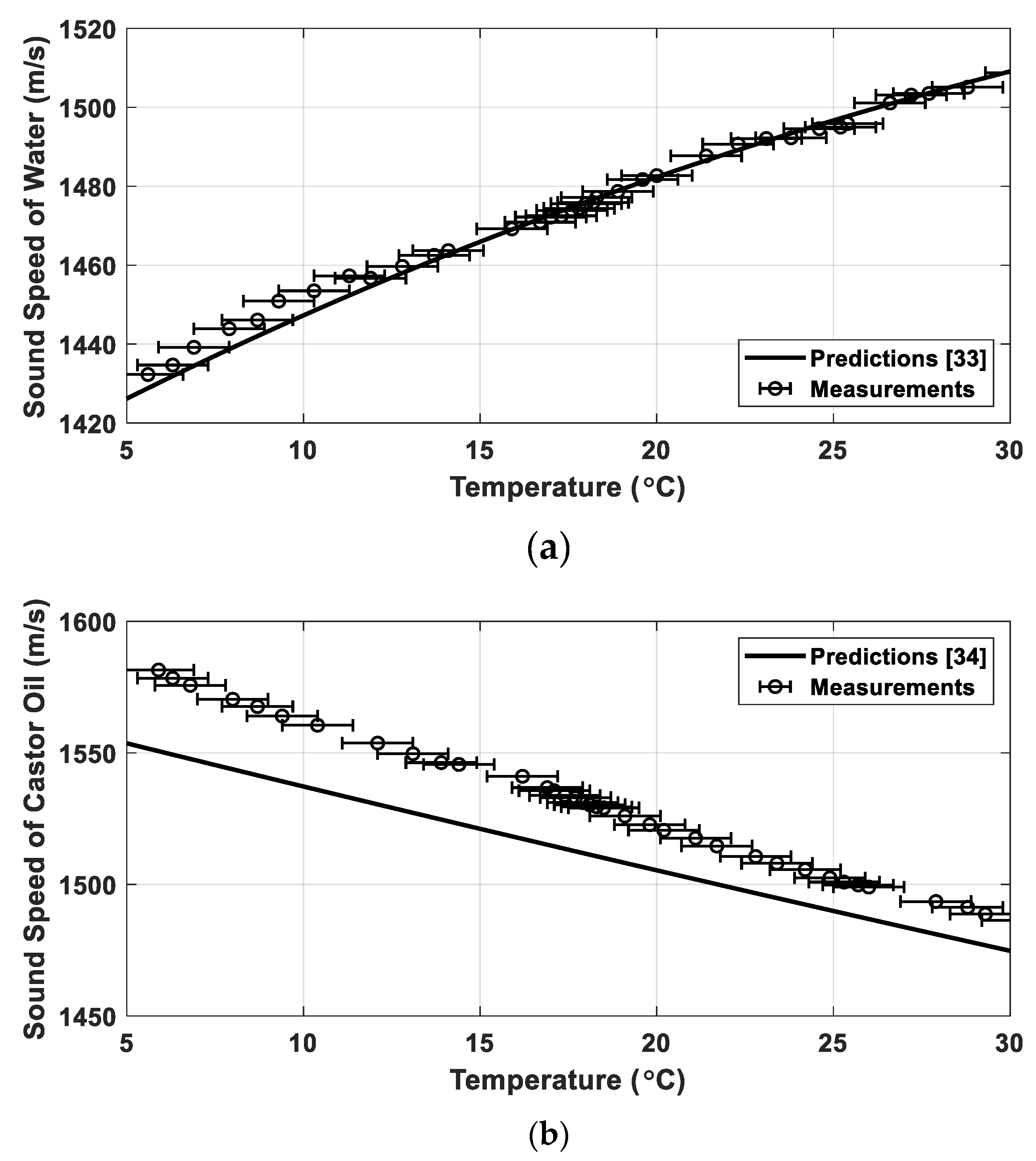
2.1. Sound-Speed Measurements
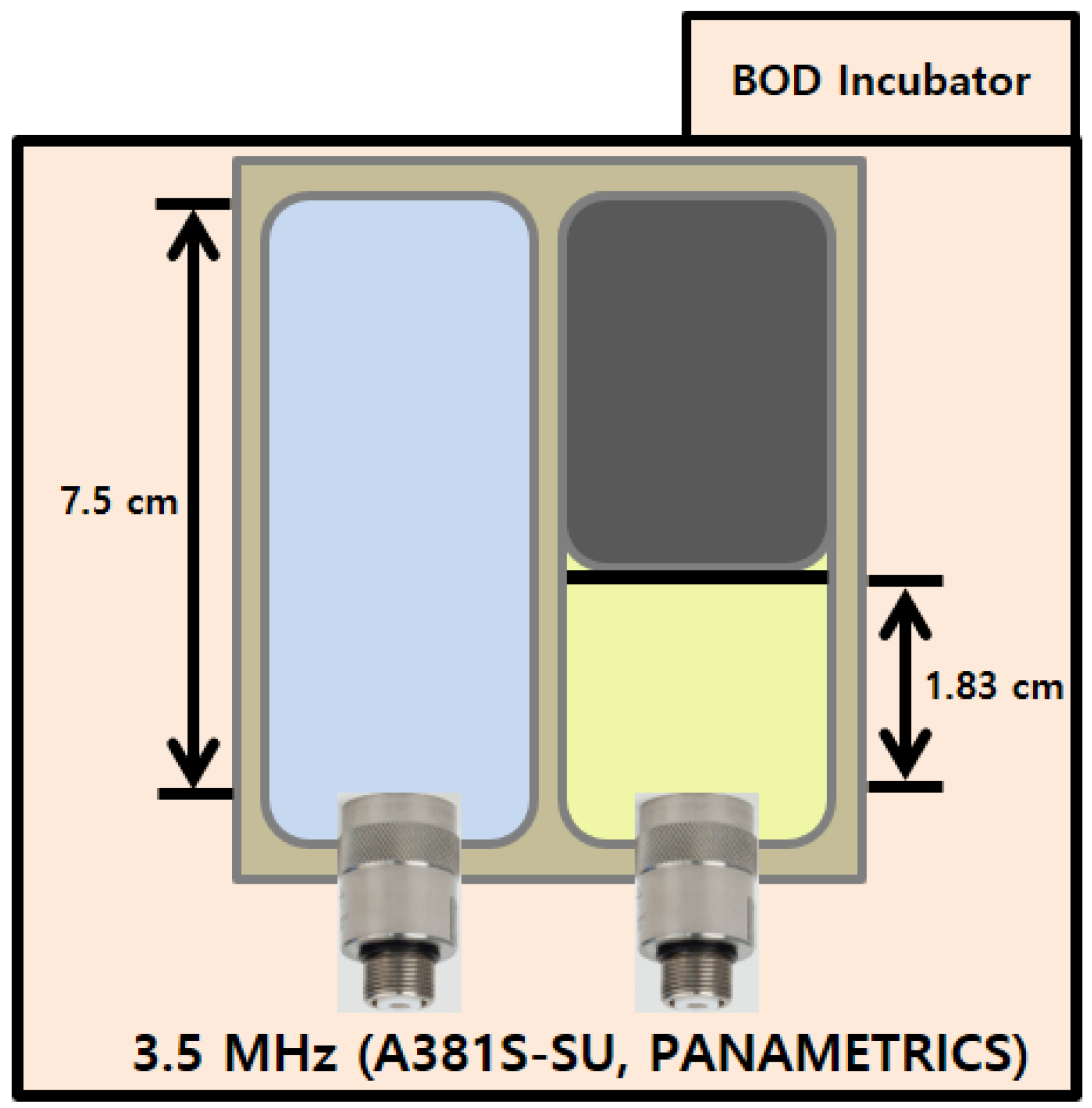
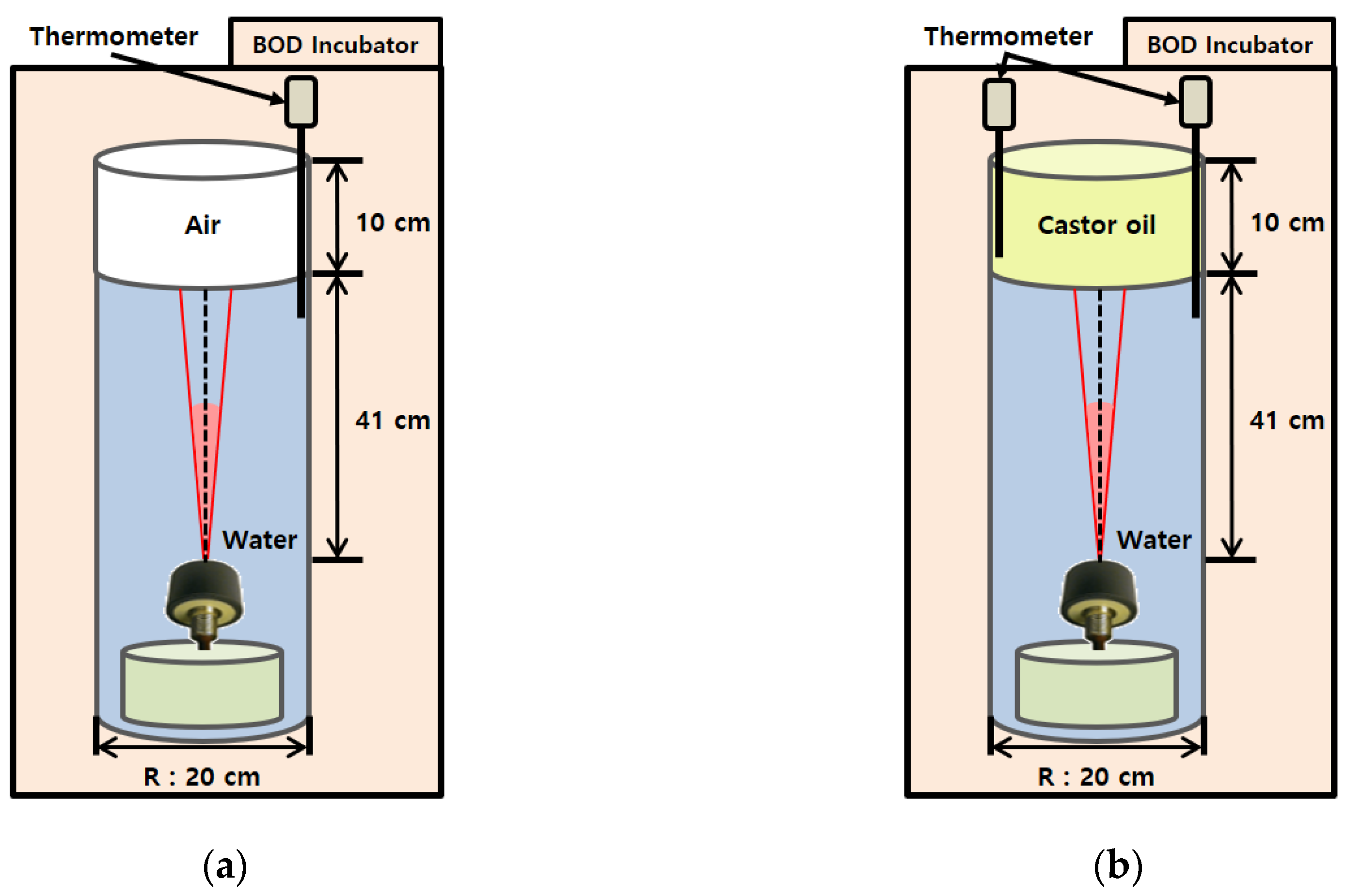
2.2. Reflection-Loss Measurements
3. Reflection-Loss Predictions
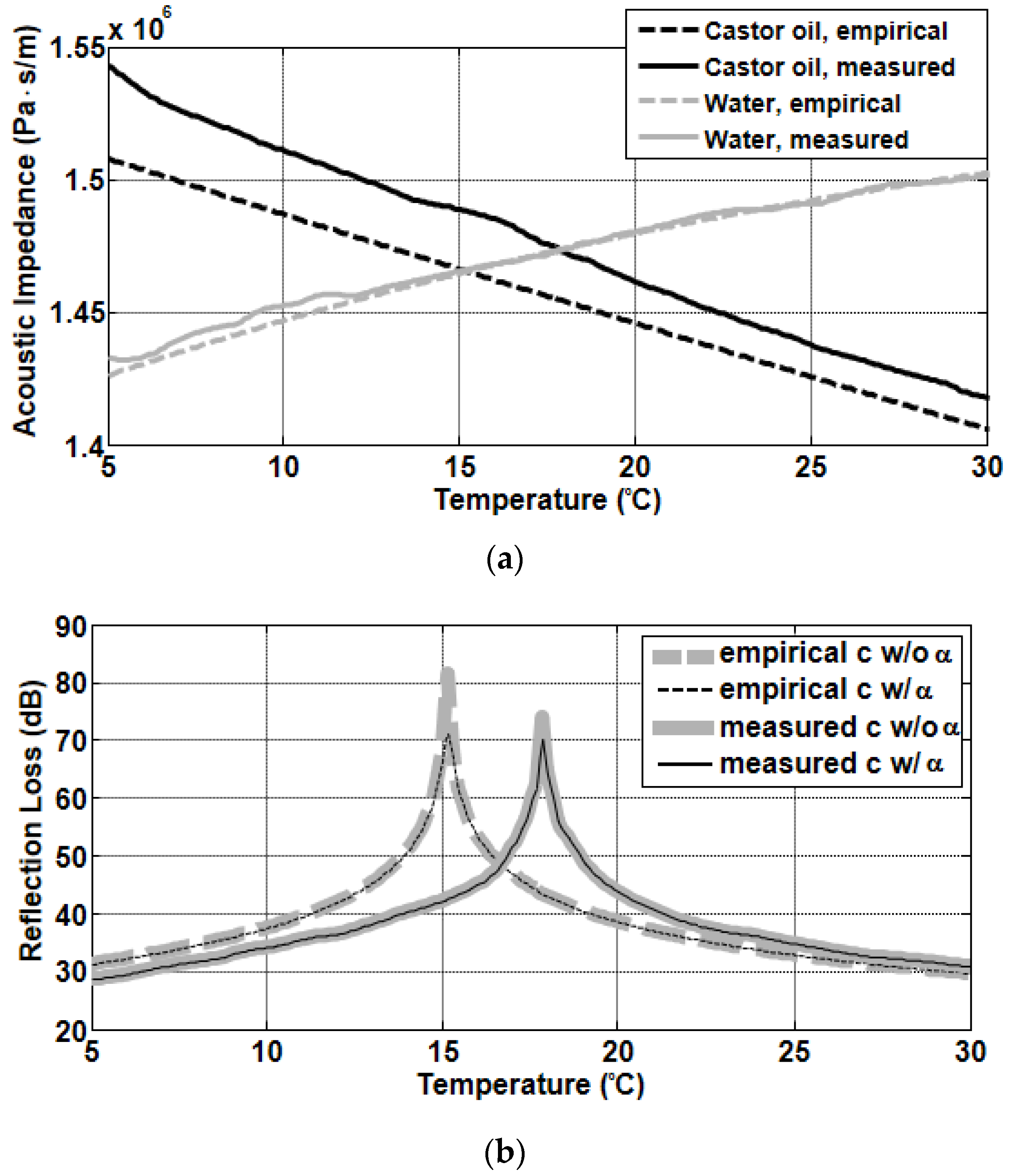
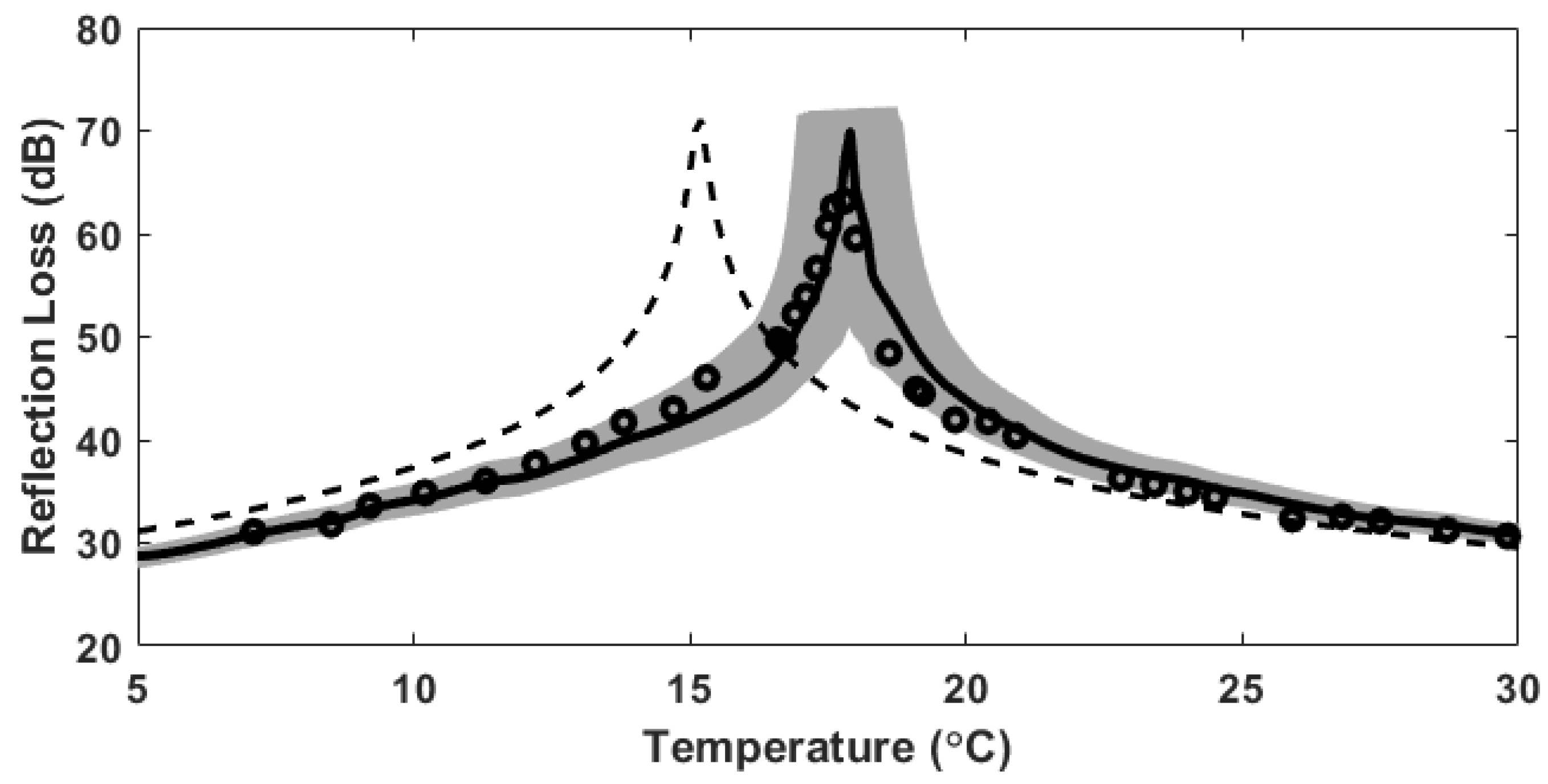
4. Results
5. Summary and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Reynolds, A.C. Boundary conditions for the numerical solution of wave propagation problem. Geophysics 1978, 43, 1099–1110. [Google Scholar] [CrossRef]
- Denneman, A.I.M.; Drijkoningen, G.G.; Smeulders, D.M.J.; Wapenaar, K. Reflection and transmission of waves at a fluid/porous-medium interface. Geophysics 2002, 67, 289–291. [Google Scholar] [CrossRef]
- Cerjan, C.; Kosloff, D.; Kosloff, R.; Reshef, M. A nonreflecting boundary condition for discrete acoustic and elastic wave equations. Geophysics 1985, 50, 705–708. [Google Scholar] [CrossRef]
- Kimura, M. Acoustic Wave Reflection from Water-saturated and Air-saturated Sediments. Jpn. J. Appl. Phys. 2002, 41, 3513–3518. [Google Scholar] [CrossRef]
- Funkhouser, T.; Tsingos, N.; Carlbom, I.; Elko, G.; Sondhi, M.; West, J.E.; Pingali, G.; Min, P.; Ngan, A. A beam tracing method for interactive architectural acoustics. J. Acoust. Soc. Am. 2004, 115, 739–756. [Google Scholar] [CrossRef] [PubMed]
- Norris, K.S.; Harvey, G.W. Sound transmission in the porpoise head. J. Acoust. Soc. Am. 1974, 56, 659–664. [Google Scholar] [CrossRef]
- Mizutani, K.; Wakatsuki, N.; Ebihara, T. Introduction of measurement techniques in ultrasonic electronic: Basic principles and recent trends. Jpn. J. Appl. Phys. 2016, 55, 07KA02. [Google Scholar] [CrossRef]
- Persson, H.W.; Hertz, C.H. Acoustic impedance matching of medical ultrasound transducers. Ultrasonics 1985, 23, 83–89. [Google Scholar] [CrossRef]
- Stoll, R.D.; Kan, T.K. Reflection of acoustic waves at a water-sediment interface. J. Acoust. Soc. Am. 1981, 70, 149–156. [Google Scholar] [CrossRef]
- Frisk, G.V. Ocean and Seabed Acoustics: A Theory of Wave Propagation; Pearson Education: Prentice Hall, NJ, USA, 1994; pp. 41, 51–53. [Google Scholar]
- Jensen, F.; Kuperman, M.; Schmidt, H. Computational Ocean Acoustics; American Institute of Physics: New York, NY, USA, 1993; pp. 40–46. [Google Scholar]
- Mackenzie, K.V. Reflection of Sound from Coastal Bottoms. J. Acoust. Soc. Am. 1960, 32, 221–231. [Google Scholar] [CrossRef]
- Kimura, M. Reflection of Plane Acoustic Waves at a Seawater-Marine Sediment Interface. Jpn. J. Appl. Phys. 1996, 35, 2948–2951. [Google Scholar] [CrossRef]
- Choi, J.W.; Dahl, P.H.; Goff, J.A. Observations of the R reflector and sediment interface reflection at the Shallow Water ’06 Central Site. J. Acoust. Soc. Am. 2008, 124, EL128–EL134. [Google Scholar] [CrossRef] [PubMed]
- Chotiros, N.P.; Lyons, A.P.; Osler, J.; Pace, N.G. Normal incidence reflection loss from a sandy sediment. J. Acoust. Soc. Am. 2002, 112, 1831–1841. [Google Scholar] [CrossRef] [PubMed]
- Holland, C.W. Direct observation of the angle of intromission in marine sediments. J. Acoust. Soc. Am. 2001, 110, 2724. [Google Scholar] [CrossRef]
- Holland, C.W. The angle of intromission in muddy sediments: Measurements and inferences. J. Acoust. Soc. Am. 2015, 137, 2283. [Google Scholar] [CrossRef]
- Holland, C.W. Coupled Scattering and Reflection Measurements in Shallow Water. IEEE J. Ocean. Eng. 2002, 27, 454–470. [Google Scholar] [CrossRef]
- Chapman, N.R.; Chapman, D.M.F. A coherent ray model of plane-wave reflection from a thin sediment layer. J. Acoust. Soc. Am. 1993, 94, 2731–2738. [Google Scholar] [CrossRef]
- Choi, J.W.; Dahl, P.H. Mid-to-High Frequency Bottom Loss in the East China Sea. IEEE J. Ocean. Eng. 2004, 29, 980–987. [Google Scholar] [CrossRef]
- Lee, C.; Cho, S.; Choi, J.W.; Shim, T.; Lee, Y.K. Geoacoustic Inversion of Mid-Frequency Bottom Loss Data in Shallow Water off the East Coast of Korea. Jpn. J. Appl. Phys. 2012, 51, 07GG01. [Google Scholar] [CrossRef]
- Kwon, H.; Choi, J.W.; Ryang, W.H.; Son, S.U.; Jung, S.K. Measurements of mid-frequency bottom-interacting signals and geoacoustic inversion in Jinhae Bay, Southeast Korea. J. Acoust. Soc. Am. 2019, 145, 1205–1211. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Fray, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics; John Wiley Sons, Inc.: New York, NY, USA, 1999; p. 527. [Google Scholar]
- Chilibon, I. Low frequency underwater piezoceramic transducer. Sens. Actuators A Phys. 2000, 85, 292–295. [Google Scholar] [CrossRef]
- Inoue, T.; Nada, T.; Tsuchiya, T.; Nakanishi, T.; Miyama, T.; Konno, M. Tonpilz Piezoeletric Transducers with Acoustic Matching Plates for Underwater Color Image Transmission. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1993, 40, 121–130. [Google Scholar] [CrossRef] [PubMed]
- Tims, A.C. A New Capped-Cylinder Design for an Underwater Sound Transducer (USRD Type F50). J. Acoust. Soc. Am. 1972, 51, 1751–1758. [Google Scholar] [CrossRef]
- Han, D.-G.; Seo, H.-C.; Choi, J.W.; Lee, M. Experiment and Simulation of Acoustic Detection for the Substitute for Sunken Hazardous and Noxious Substances Using the High Frequency Active Sonar. J. Korean Soc. Mar. Environ. Saf. 2018, 24, 459–466. [Google Scholar] [CrossRef]
- Han, D.G.; Choi, J.W.; Son, S.U. Tank experiment and simulation of sunken hazardous and noxious substances detection using high frequency active sonar. In Proceedings of the Regional Conference on Acoustics and Vibration 2017 (RECAV 2017), Bali, Indonesia, 27–28 November 2017. [Google Scholar]
- Han, D.G.; Seo, H.C.; Choi, J.W.; Lee, M.; Hwang, H.J. Observation of the Temperature of Intromission at Water-Castor Oil Interface. In Proceedings of the 39th Symposium on UltraSonic Electronics (USE 2018), Tokyo, Japan, 29–31 October 2018. [Google Scholar]
- Patel, V.R.; Dumancas, G.G.; Viswanath, L.C.K.; Maples, R.; Subong, B.J.J. Castor Oil: Properties, Uses, and Optimization of Processing Parameters in Commercial Production. Lipid Insights 2016, 9, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Szabo, T.L. Causal theories and data for acoustic attenuation obeying a frequency power law. J. Acoust. Soc. Am. 1995, 97, 14–24. [Google Scholar] [CrossRef]
- Francois, R.E; Garrison, G.R. Sound absorption based on ocean measurements. Part II: Boric acid contribution and equation for total absorption. J. Acoust. Soc. Am. 1982, 72, 1879–1890. [Google Scholar] [CrossRef]
- Del Grosso, V.A.; Mader, C.W. Speed of Sound in Pure Water. J. Acoust. Soc. Am. 1972, 52, 1442–1446. [Google Scholar] [CrossRef]
- Timme, R.W. Speed of Sound in Castor Oil. J. Acoust. Soc. Am. 1972, 52, 989–992. [Google Scholar] [CrossRef]
- Lurton, X. An Introduction to Underwater Acoustics, 2nd ed.; Springer: London, UK, 2010; p. 15. [Google Scholar]
- Potter, M.C.; Wiggert, D.C.; Ramadan, B.H. Mechanics of Fluids, 4th ed.; Cengage learning: Stamford, CT, USA, 2011; p. 595. [Google Scholar]
- Bilaniuk, N.; Wong, G.S.K. Speed of sound in pure water as a function of temperature. J. Acoust. Soc. Am. 1993, 93, 1609–1612. [Google Scholar] [CrossRef]
- Thorne, P.D.; Vincent, C.E.; Hardcastle, P.J.; Rehman, S.; Pearson, N. Measuring suspended sediment concentrations using acoustic backscatter devices. Mar. Geol. 1991, 98, 7–16. [Google Scholar] [CrossRef]
- Medwin, H.; Clay, C.S. Fundamentals of Acoustical Oceanography; Academic Press: Boston, MA, USA, 1998; p. 712. [Google Scholar]
- Kim, E.; Lee, H.; Na, J.; Choi, J.W.; Kang, D. 5-MHz acoustic-backscattering measurements of Cochlodinium polykrikoides blooms in Korean coastal waters. ICES J. Mar. Sci. 2010, 67, 1–7. [Google Scholar] [CrossRef]
- Vidmar, P.J. Ray path analysis of sediment shear wave effects on bottom reflection loss. J. Acoust. Soc. Am. 1980, 68, 639–648. [Google Scholar] [CrossRef]
- Ainslie, M.A.; Robins, A.J.; Prior, M.K. Benchmark solutions of plane wave bottom reflection loss. J. Acoust. Soc. Am. 1998, 104, 3305–3312. [Google Scholar] [CrossRef]
- Tanaka, M.; Girard, G.; Davis, R.; Peuto, A.; Bignell, N. Recommended table for the density of water between 0 °C and 40 °C based on recent experimental reports. Metrologia 2001, 38, 301–309. [Google Scholar] [CrossRef]
- Treeby, B.E.; Cox, B.T.; Zhang, E.Z.; Patch, S.K.; Beard, P.C. Measurement of Broadband Temperature Dependent Ultrasonic Attenuation and Dispersion Using Photoacoustic. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 1666–1676. [Google Scholar] [CrossRef] [PubMed]
- Beamiss, G.A.; Robinson, S.P.; Hayman, G.; Esward, T.J. Determination of the Variation in Free-Field Hydrophone Response with Temperature and Depth. Acta Acust. United Acust. 2002, 88, 799–802. [Google Scholar]
- Buren, A.L.V.; Drake, R.M.; Paolero, A.E. Temperature dependence of the sensitivity of hydrophone standards used in international comparisons. Metrologia 1999, 36, 281–285. [Google Scholar] [CrossRef]
- Meribout, M.; Habli, M.; Al-Naamany, A.; Al-Busaidi, K. A New Ultrasonic-based device for Accurate Measurement of Oil, Emulsion, and Water Levels in Oil Tanks. In Proceedings of the IEEE Instrumentation and Measurement Technology Conference, Como, Italy, 18–20 May 2004; pp. 1942–1947. [Google Scholar]
- Lipper, A.; Borden, J. Urethane Transducer Encapsulation versus Oil Filled Boot Encapsulation of Piezoelectric Transducers. In Proceedings of the 2012 OCEANS, Hampton Roads, VA, USA, 14–19 October 2012. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, D.-G.; Seo, H.-C.; Cho, S.; Choi, J.W. Measurements of Normal Incidence Reflection Loss as a Function of Temperature at the Water-Castor Oil Interface. Sensors 2019, 19, 3289. https://doi.org/10.3390/s19153289
Han D-G, Seo H-C, Cho S, Choi JW. Measurements of Normal Incidence Reflection Loss as a Function of Temperature at the Water-Castor Oil Interface. Sensors. 2019; 19(15):3289. https://doi.org/10.3390/s19153289
Chicago/Turabian StyleHan, Dong-Gyun, Him-Chan Seo, Sungho Cho, and Jee Woong Choi. 2019. "Measurements of Normal Incidence Reflection Loss as a Function of Temperature at the Water-Castor Oil Interface" Sensors 19, no. 15: 3289. https://doi.org/10.3390/s19153289
APA StyleHan, D.-G., Seo, H.-C., Cho, S., & Choi, J. W. (2019). Measurements of Normal Incidence Reflection Loss as a Function of Temperature at the Water-Castor Oil Interface. Sensors, 19(15), 3289. https://doi.org/10.3390/s19153289






