Asymmetry Analysis of the Resonance Curve in Resonant Integrated Optical Gyroscopes
Abstract
:1. Introduction
2. System Structure of the Resonant Integrated Optical Gyroscope
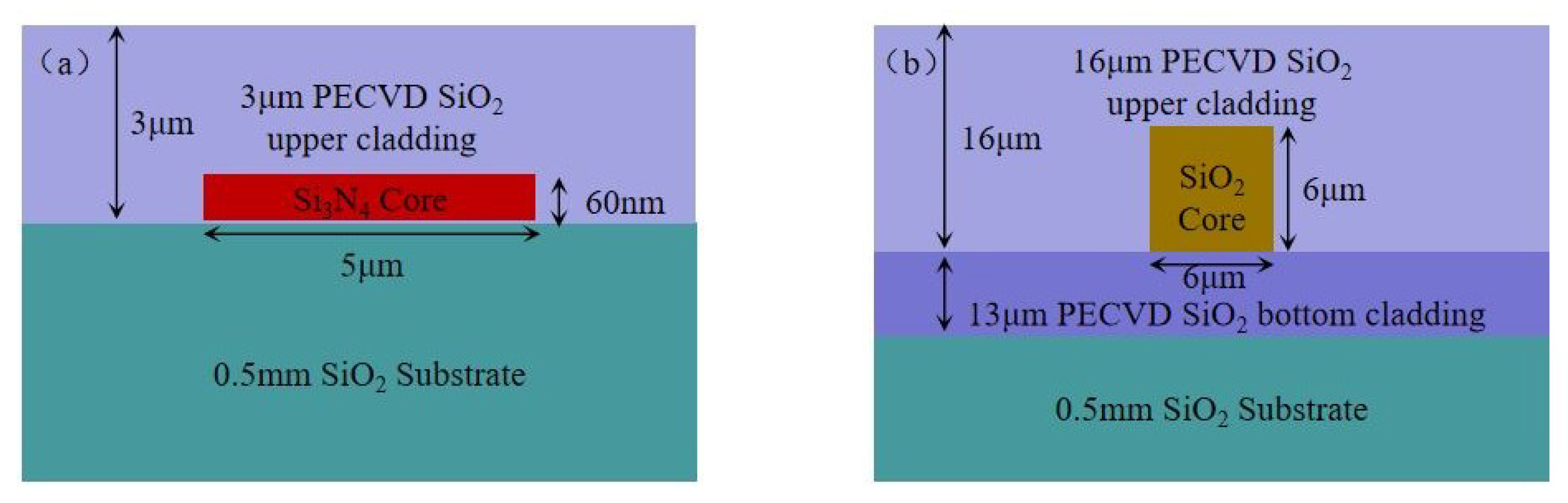
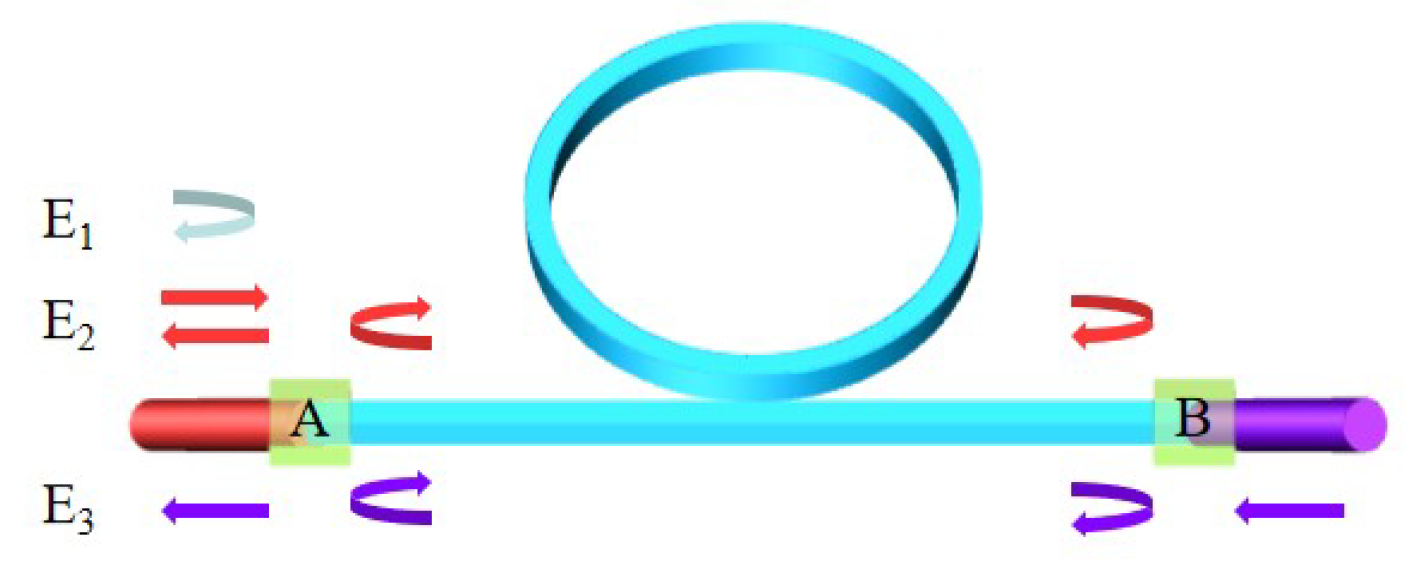
2.1. The RIOG System Based on the Phase Modulation Spectroscopy Technique
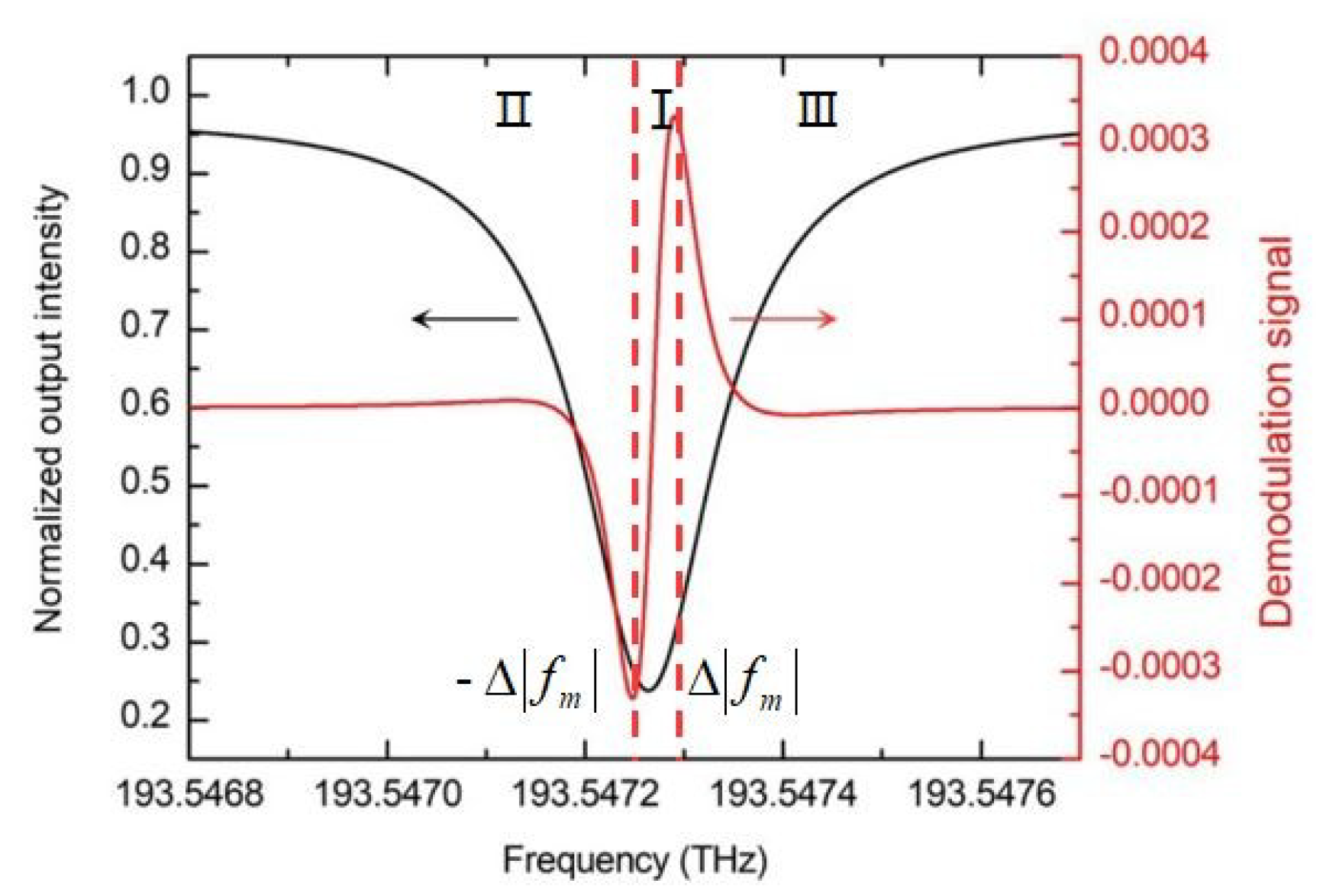
2.2. The Resonance Curve and Demodulation Curve of the RIOG
3. Analysis Asymmetry of the Resonance Curve
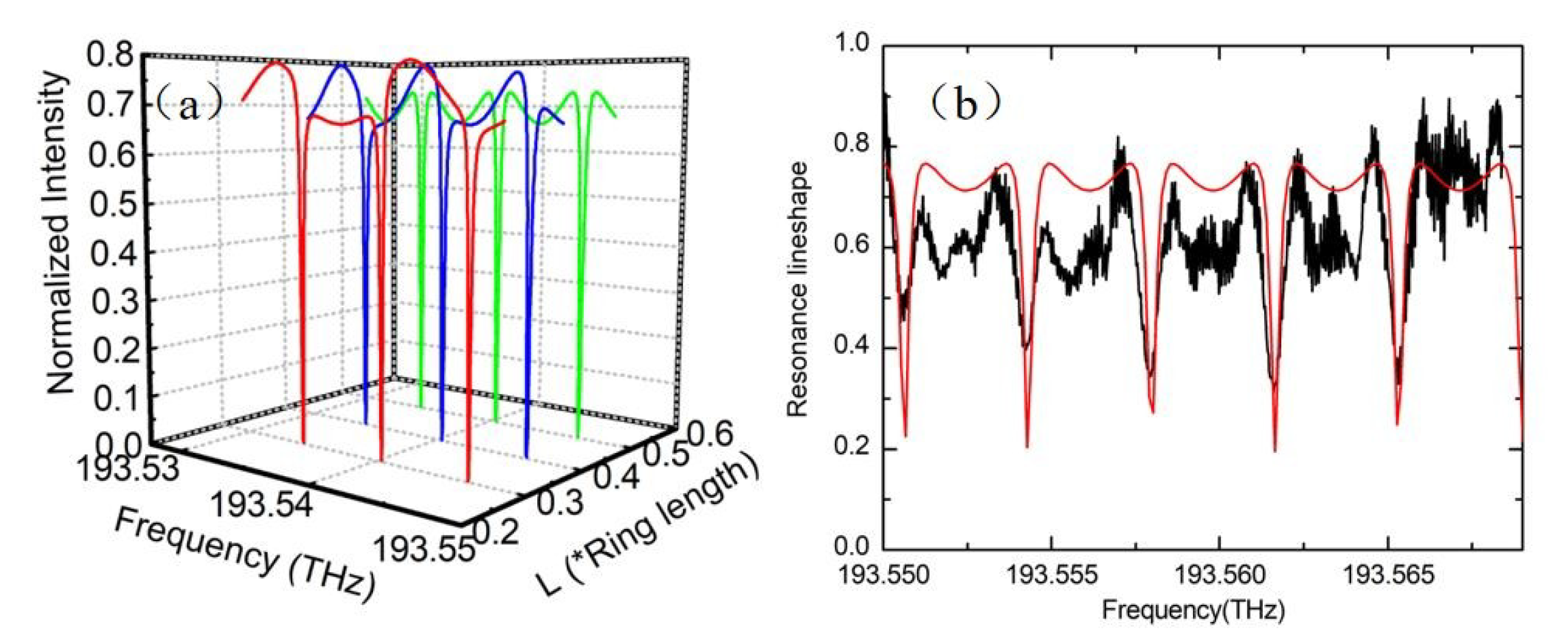
3.1. Materials and Methods
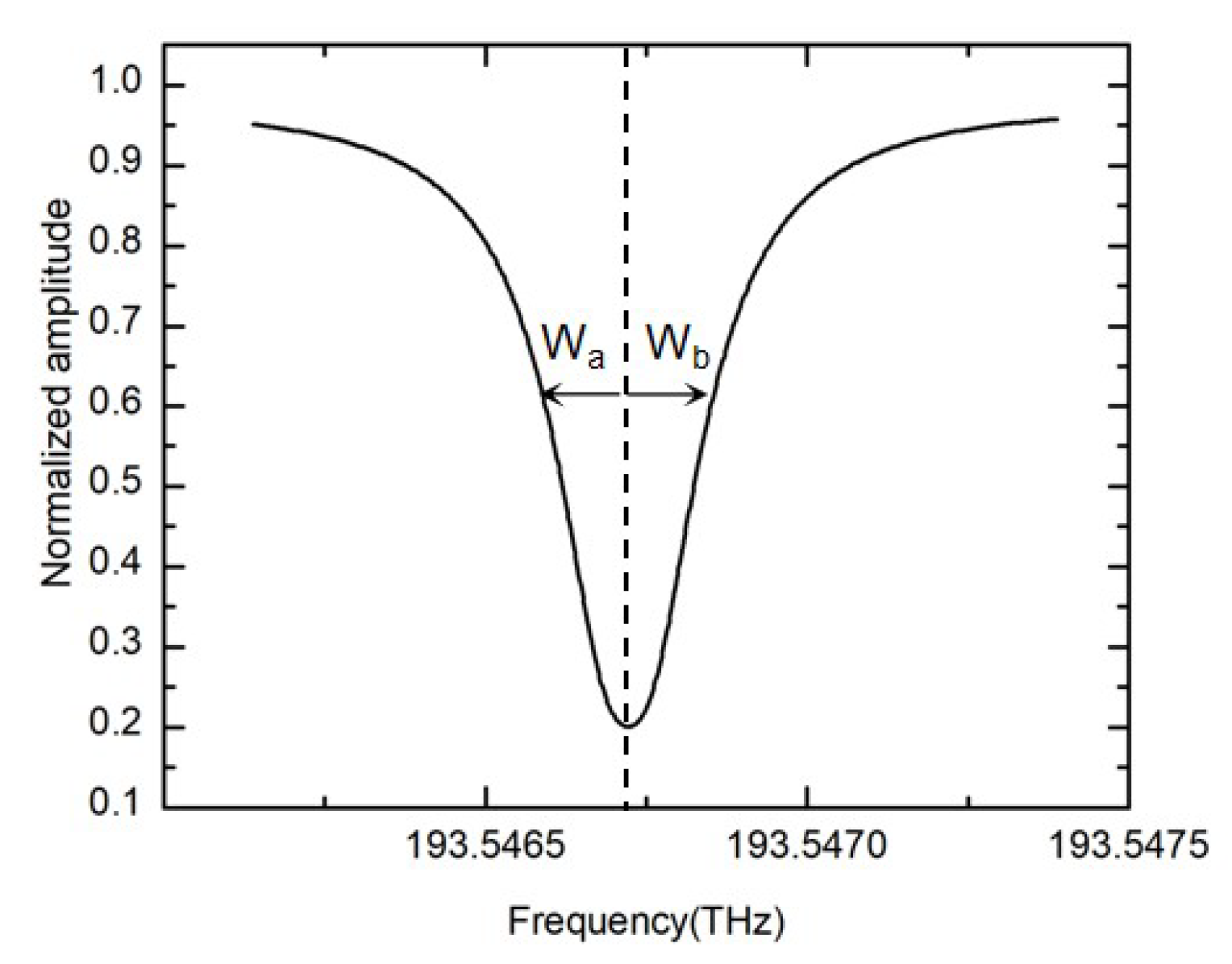
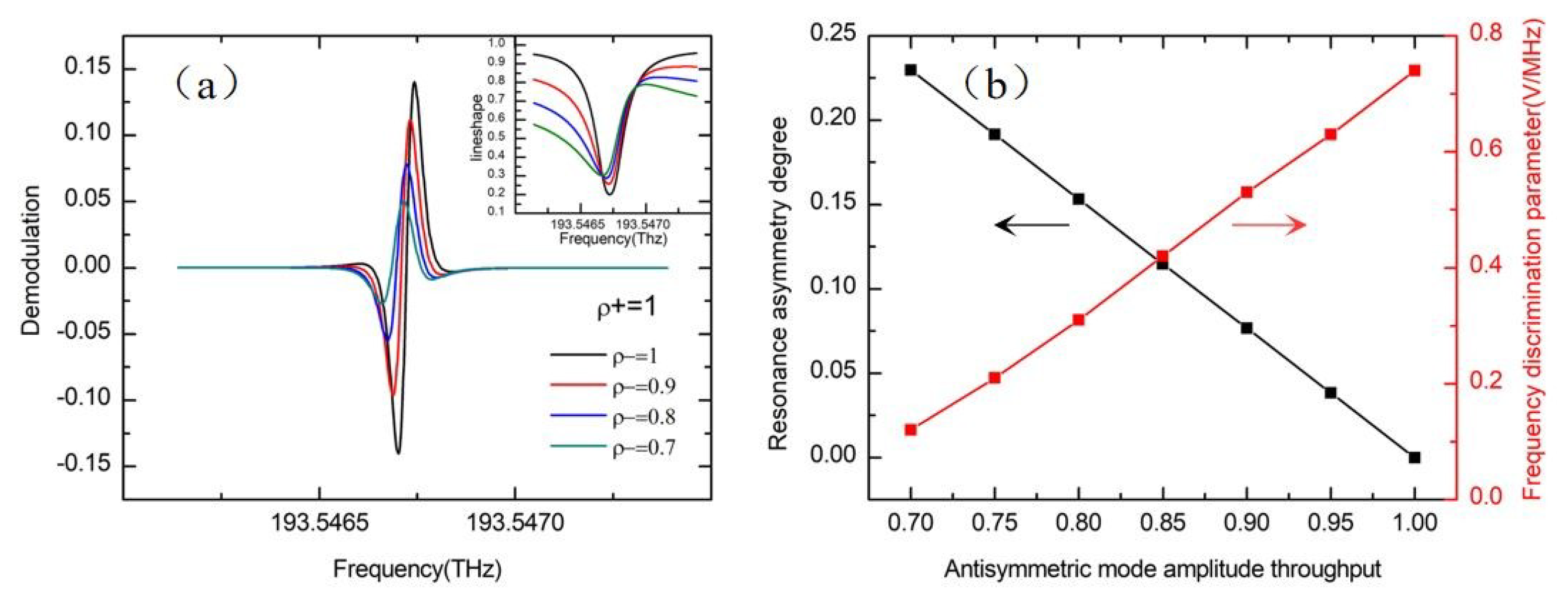
3.2. Resonance Asymmetry Degree
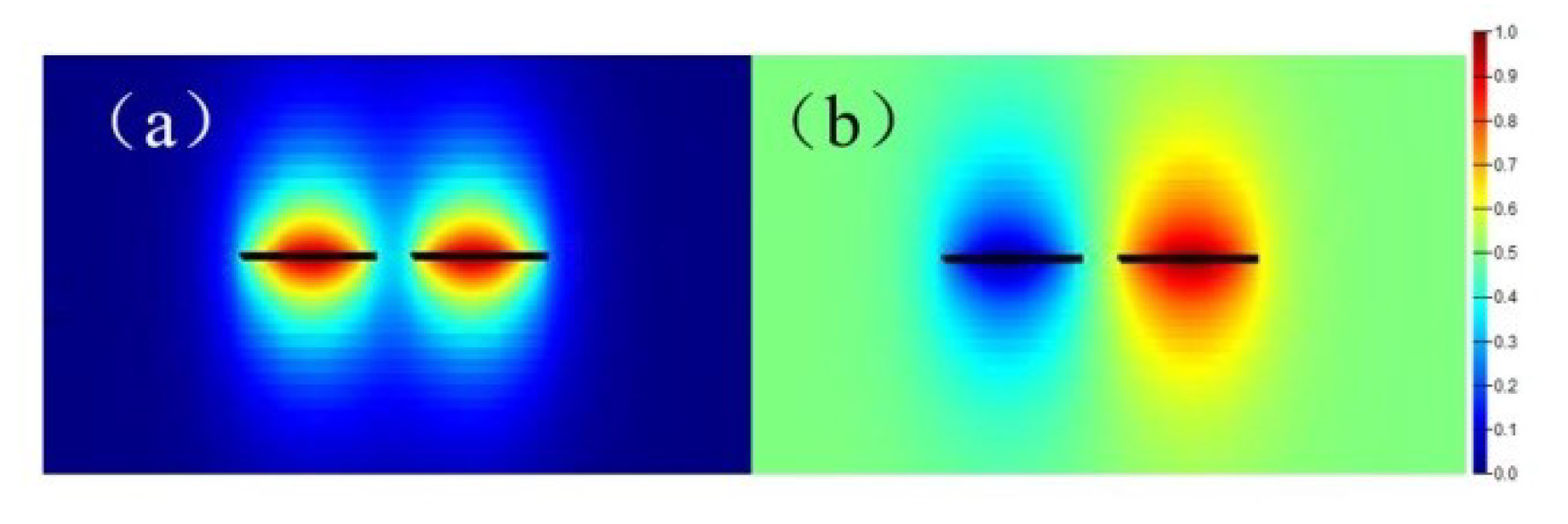
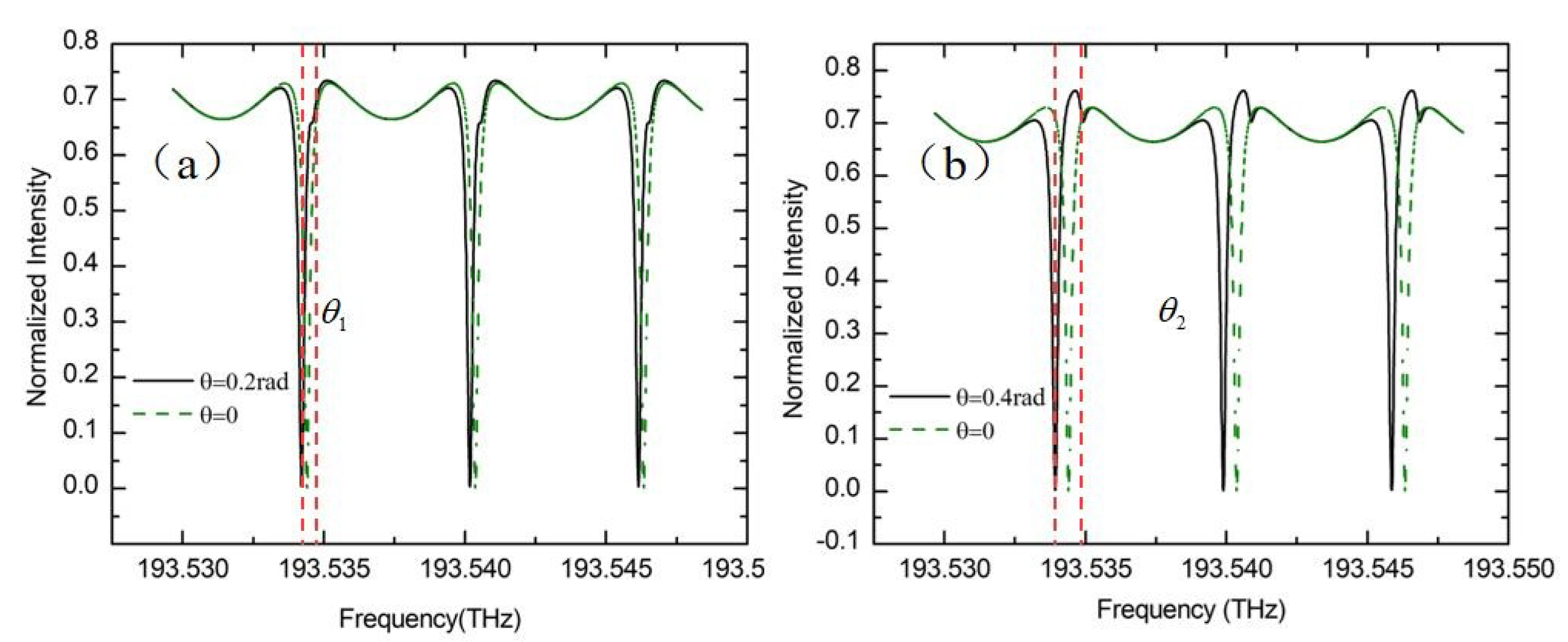
3.3. Normal Mode Effect
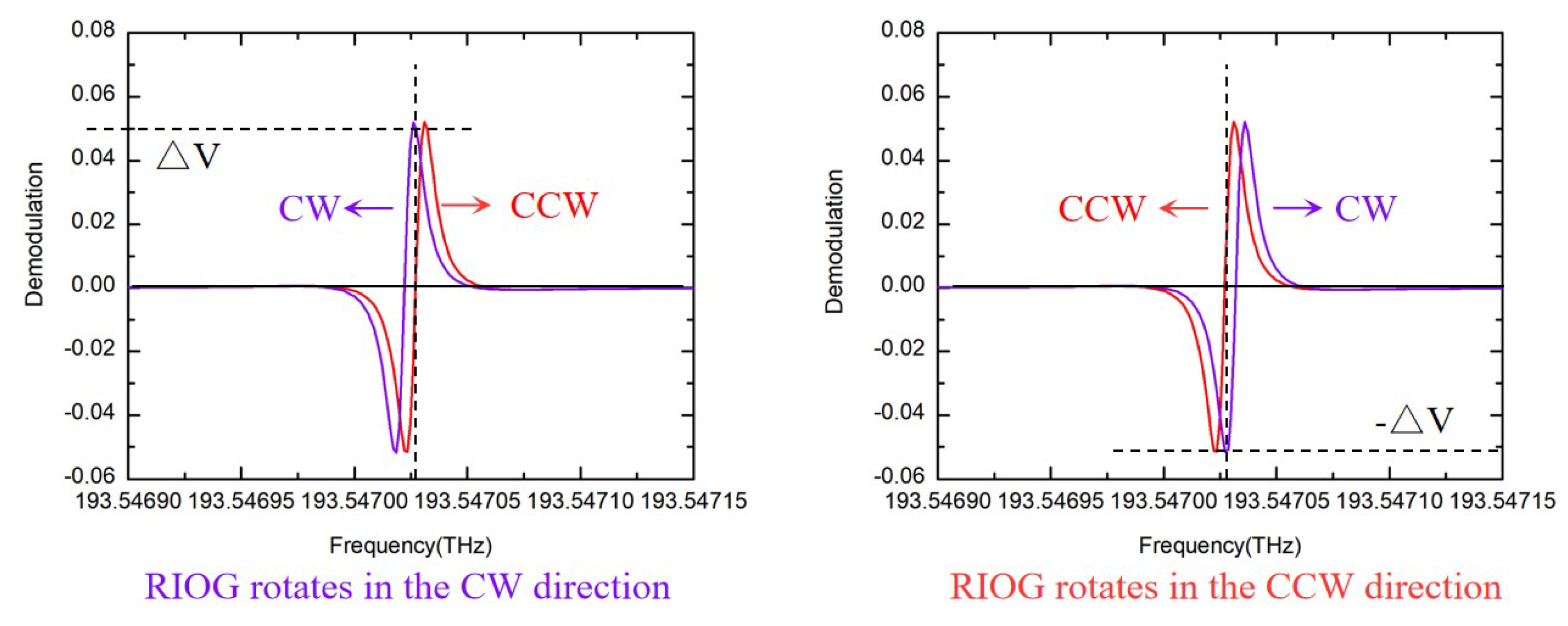
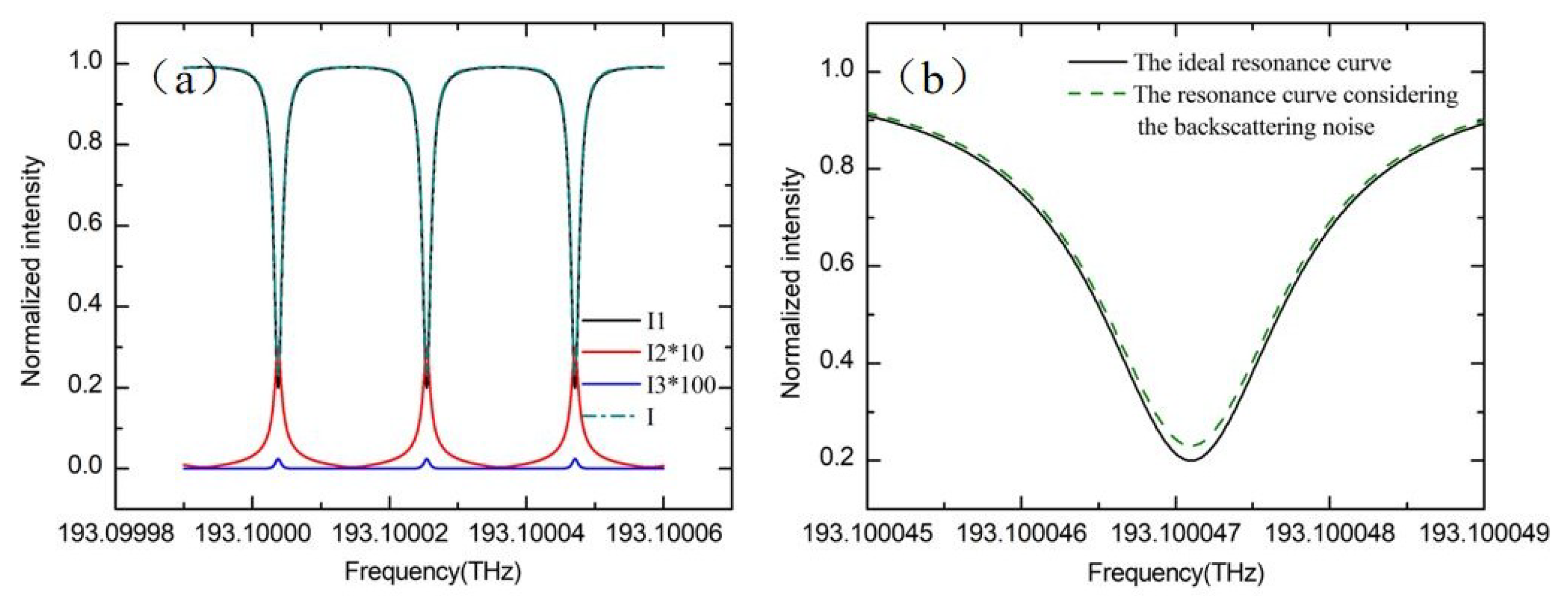
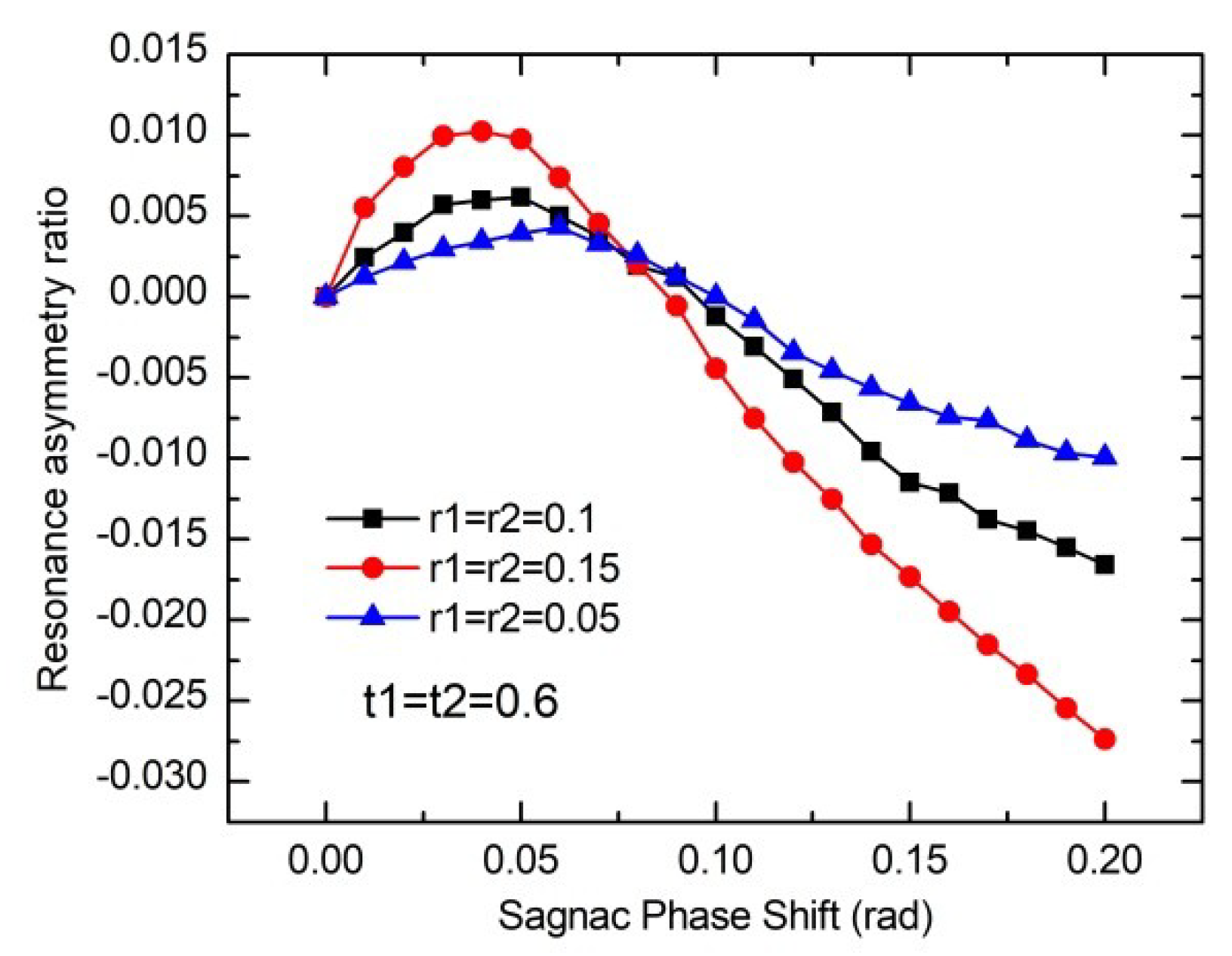
3.4. Rayleigh Backscattering Noise
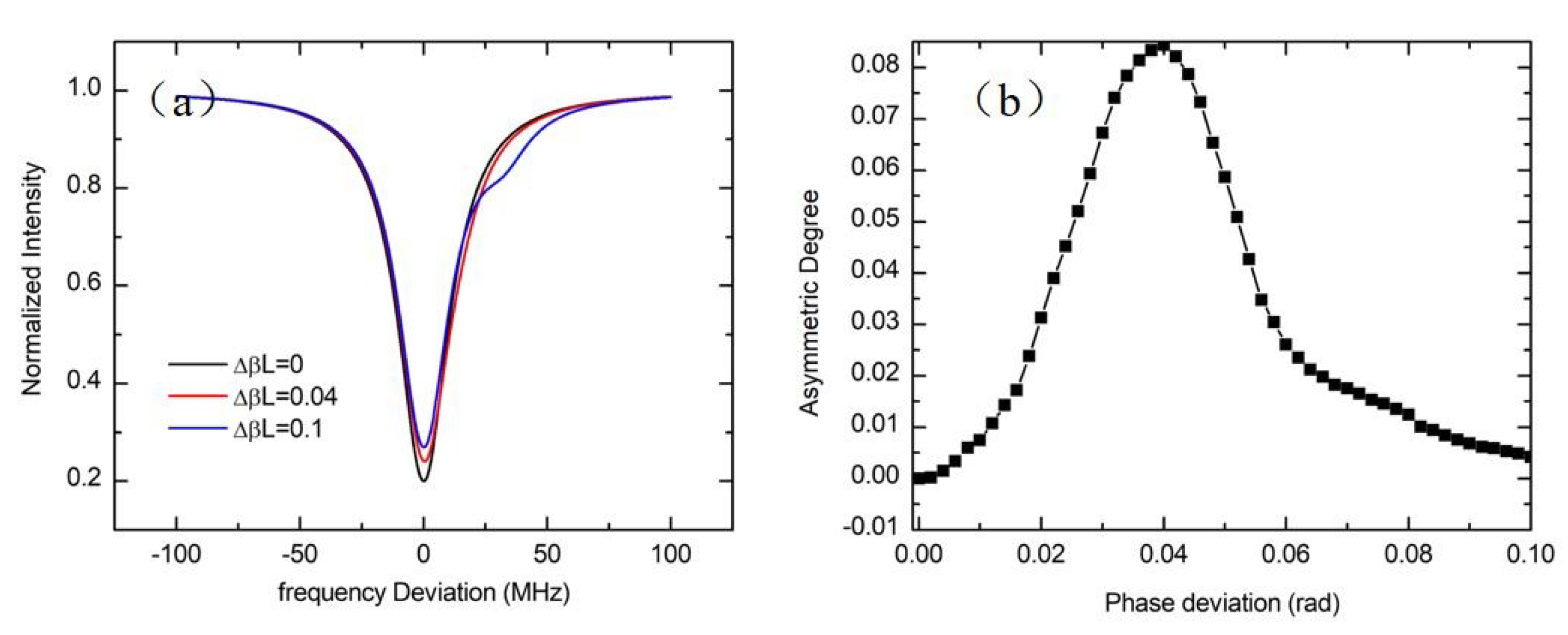
3.5. Backreflection Noise
3.6. Polarization Noise
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, L.; Zhang, C.; Gao, S.; Wang, T.; Lin, T.; Li, X. Application of Fast Dynamic Allan Variance for the Characterization of FOGs-Based Measurement While Drilling. Sensors 2016, 16, 2078. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Ma, H.; Li, H.; Jin, Z. Single-polarization fiber-pigtailed high-finesse silica waveguide ring resonator for a resonant micro-optic gyroscope. Opt. Lett. 2017, 42, 3658–3661. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, J.; Wang, L.; Jin, Z. Development and Evaluation of Optical Passive Resonant Gyroscopes. J. Lightwave Technol. 2017, 35, 3546–3554. [Google Scholar] [CrossRef]
- Campanella, C.E.; Ciminelli, C.; Dell’Olio, F.; Armenise, M.N. Photonic technologies for angular velocity sensing. Adv. Opt. Photonics 2010, 2, 370–404. [Google Scholar]
- Vali, V.; Shorthill, R.W. Fiber ring interferometer. Appl. Opt. 1976, 15, 1099–1100. [Google Scholar] [CrossRef]
- Ezekiel, S. Optical Gyroscope Options: Principles and Challenges. In Proceedings of the Optical Fiber Sensors in Proceedings Optical Fiber Sensors, Cancun, Mexico, 23–27 October 2006. [Google Scholar] [CrossRef]
- Li, Z.; He, N.; Sun, X.; Jin, C.; Liu, C.; Wu, X. Analysis of Resonance Asymmetry Phenomenon in Resonant Fiber Optic Gyro. Sensors 2018, 18, 696. [Google Scholar] [CrossRef] [PubMed]
- Khial, P.P.; White, A.D.; Hajimiri, A. Nanophotonic optical gyroscope with reciprocal sensitivity enhancement. Nat. Photonics 2018, 12, 671–675. [Google Scholar] [CrossRef] [Green Version]
- Monovoukas, C. Integrated optical gyroscopes offering low cost, small size and vibration immunity. Proc. SPIE Int. Soc. Opt. Eng. 2000, 3936, 293–300. [Google Scholar]
- Dell’Olio, F.; Ciminelli, C.; Armenise, M.N.; Soares, F.M.; Rehbein, W. Design, fabrication, and preliminary test results of a new InGaAsP/InP high-Q ring resonator for gyro applications. In Proceedings of the International Conference on Indium Phosphide & Related Materials, Santa Barbara, CA, USA, 27–30 August 2012. [Google Scholar]
- Ciminelli, C.; Dell’Olio, F.; Armenise, M.N. High-Q Spiral Resonator for Optical Gyroscope Applications: Numerical and Experimental Investigation. IEEE Photonics J. 2012, 4, 1844–1854. [Google Scholar] [CrossRef]
- Ciminelli, C.; Dell’Olio, F.; Armenise, M.N. High performance inp ring resonator for new generation monolithically integrated optical gyroscopes. Opt. Express 2013, 21, 556–564. [Google Scholar] [CrossRef]
- Wei, L.; Ilchenko, V.S.; Savchenkov, A.A.; Dale, E.; Eliyahu, D.; Matsko, A.B.; Maleki, L. Resonant microphotonic gyroscope. Optica 2017, 4, 114–117. [Google Scholar]
- Ciminelli, C.; Agostino, D.D.; Carnicella, G.; Olio, F.D.; Conteduca, D.; Ambrosius, H.P.M.M.; Smit, M.K.; Armenise, M.N. A High-Q InP Resonant Angular Velocity Sensor for a Monolithically Integrated Optical Gyroscope. IEEE Photonics J. 2015, 8, 1–19. [Google Scholar] [CrossRef]
- Wu, B.; Yu, Y.; Xiong, J.; Zhang, X. Silicon Integrated Interferometric Optical Gyroscope. Sci. Rep. 2018, 8, 8766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gundavarapu, S.; Belt, M.; Huffman, T.A.; Tran, M.A.; Komljenovic, T.; Bowers, J.E.; Blumenthal, D.J. Interferometric Optical Gyroscope Based on an Integrated Si3N4 Low-Loss Waveguide Coil. J. Lightwave Technol. 2018, 36, 1185–1191. [Google Scholar] [CrossRef]
- Tran, M.A.; Komljenovic, T.; Hulme, J.C.; Kennedy, M.; Blumenthal, D.J.; Bowers, J.E. Integrated optical driver for interferometric optical gyroscopes. Opt. Express 2017, 25, 3826–3840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sudharsanan, S.; Renan, M.; Daniel, B.; Bowers, J.E. Design of integrated hybrid silicon waveguide optical gyroscope. Opt. Express 2014, 22, 24988–24993. [Google Scholar]
- Liu, N.; Niu, Y.; Feng, L.; Jiao, H.; Wang, X. Suppression of backscattering induced noise by the sideband locking technique in a resonant fiber optic gyroscope. Chin. Opt. Lett. 2018, 16, 010608. [Google Scholar]
- Iwatsuki, K.; Hotate, K.; Higashiguchi, M. Eigenstate of polarization in a fiber ring resonator and its effect in an optical passive ring-resonator gyro. Appl. Opt. 1986, 25, 2606–2612. [Google Scholar] [CrossRef]
- Youngquist, R.; Stokes, L.; Shaw, H. Effects of normal mode loss in dielectric waveguide directional couplers and interferometers. IEEE J. Quantum Electron. 1983, 19, 1888–1896. [Google Scholar] [CrossRef]
- Hui, L.; Liying, L.; Zhili, L.; Qiwei, W.; Xiao, W.; Lishuang, F. Double closed-loop control of integrated optical resonance gyroscope with mean-square exponential stability. Opt. Express 2018, 26, 1145–1160. [Google Scholar]
- Iwatsuki, K.; Hotate, K.; Higashiguchi, M. Effect of Rayleigh backscattering in an optical passive ring-resonator gyro. Appl. Opt. 1984, 23, 3916–3924. [Google Scholar] [CrossRef] [PubMed]
- Post, E.J. Sagnac Effect. Rev. Mod. Phys. 1967, 39, 475–493. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, H.; Jin, Z.; Ding, C. Open-loop operation experiments in a resonator fiber-optic gyro using the phase modulation spectroscopy technique. Appl. Opt. 2006, 45, 7961–7965. [Google Scholar] [CrossRef] [PubMed]
- Mao, H.; Ma, H.; Jin, Z. Resonator Micro-Optic Gyroscope Based on the Double Phase Modulation Technique. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 16–21 May 2010; p. JWA52. [Google Scholar]
- Wang, J.; Feng, L.; Tang, Y.; Zhi, Y. Resonator integrated optic gyro employing trapezoidal phase modulation technique. Adv. Photonics 2015, 40, 155–158. [Google Scholar] [CrossRef] [PubMed]
- Ying, D.; Ma, H.; Jin, Z. Resonator fiber optic gyro using the triangle wave phase modulation technique. Opt. Commun. 2008, 281, 580–586. [Google Scholar] [CrossRef]
- Feng, L.S.; Lei, M.; Liu, H.L.; Zhi, Y.Z.; Wang, J.J. Suppression of backreflection noise in a resonator integrated optic gyro by hybrid phase-modulation technology. Appl. Opt. 2013, 52, 1668–1675. [Google Scholar] [CrossRef]
- Lei, M.; Feng, L.; Zhi, Y.; Liu, H.; Wang, J.; Ren, X.; Su, N. Current modulation technique used in resonator micro-optic gyro. Appl. Opt. 2013, 52, 307–313. [Google Scholar] [CrossRef]
- Hotate, K.; Harumoto, M. Resonator fiber optic gyro using digital serrodyne modulation. J. Lightwave Technol. 2002, 15, 466–473. [Google Scholar] [CrossRef]
- Ebberg, A.; Schiffner, G. Closed-loop fiber-optic gyroscope with a sawtooth phase-modulated feedback. Opt. Lett. 1985, 10, 300–302. [Google Scholar] [CrossRef]
- Ma, H.; He, Z.; Hotate, K. Reduction of Backscattering Induced Noise by Carrier Suppression in Waveguide-Type Optical Ring Resonator Gyro. J. Lightwave Technol. 2011, 29, 85–90. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, H.; Jin, Z. Resonance asymmetry induced bias errors in waveguide type optical passive resonator gyro. Appl. Opt. 2012, 51, 2373–2378. [Google Scholar] [CrossRef] [PubMed]
- Chang, X.; Ma, H.; Jin, Z. Resonance asymmetry phenomenon in waveguide-type optical ring resonator gyro. Opt. Commun. 2012, 285, 1134–1139. [Google Scholar] [CrossRef]
- Yao, F.; He, Y.; Yang, F.; Li, Z. Effect of Backreflection and Normal Mode Loss on the Transmission of Waveguide Ring Resonator. Chin. J. Lasers 2018, 45, 513001-1. [Google Scholar]
- Nakazawa, M. Rayleigh backscattering theory for single-mode optical fibers. J. Opt. Soc. Am. 1983, 73, 1175–1180. [Google Scholar] [CrossRef]
- Philen, D.; White, I.; Kuhl, J.; Mettler, S. Single-mode fiber OTDR: Experiment and theory. Quantum Electron. IEEE J. 1982, 18, 1499–1508. [Google Scholar] [CrossRef]
- Wang, J.; Feng, L.; Wang, Q.; Jiao, H.; Wang, X. Suppression of backreflection error in resonator integrated optic gyro by the phase difference traversal method. Opt. Lett. 2016, 41, 1586–1589. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Feng, L.; Zhi, Y.; Liu, H.; Wang, W.; Lei, M. Reduction of backreflection noise in resonator micro-optic gyro by integer period sampling. Appl. Opt. 2013, 52, 7712–7717. [Google Scholar] [CrossRef]
- Zhang, X. Analysis on Two-Reflection-Dots Model outside Resonator of R-MOG. Chin. J. Sens Actuators 2009, 22, 811–815. [Google Scholar]
- Shah, V.; Curtis, L.; Young, W.C. Novel transmitted power variations in single-mode fiber joints with obliquely polished endfaces. J. Lightwave Technol. 2002, 7, 1478–1483. [Google Scholar] [CrossRef]
- Yan, Y.; Chen, Y.; Ma, H.; Jin, Z. Polarization-fluctuation Induced Drift in Resonator Micro Optic Gyro. In Proceedings of the 2012 Asia Communications and Photonics Conference (ACP), Guangzhou, China, 7–10 November 2012. [Google Scholar]
- Morthier, G.; Zhang, H.; Teng, J.; Zhao, M.; Dumon, P.; Baets, R.; Bogaerts, W.; Jian, X.; Han, X. Athermal Silicon-on-insulator ring resonators by overlaying a polymer cladding on narrowed waveguides. Opt. Express 2009, 17, 14627–14633. [Google Scholar] [Green Version]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.M.; Yang, F.H.; Yan, W.; Han, W.H.; Li, Z.F. Asymmetry Analysis of the Resonance Curve in Resonant Integrated Optical Gyroscopes. Sensors 2019, 19, 3305. https://doi.org/10.3390/s19153305
He YM, Yang FH, Yan W, Han WH, Li ZF. Asymmetry Analysis of the Resonance Curve in Resonant Integrated Optical Gyroscopes. Sensors. 2019; 19(15):3305. https://doi.org/10.3390/s19153305
Chicago/Turabian StyleHe, Yu Ming, Fu Hua Yang, Wei Yan, Wei Hua Han, and Zhao Feng Li. 2019. "Asymmetry Analysis of the Resonance Curve in Resonant Integrated Optical Gyroscopes" Sensors 19, no. 15: 3305. https://doi.org/10.3390/s19153305
APA StyleHe, Y. M., Yang, F. H., Yan, W., Han, W. H., & Li, Z. F. (2019). Asymmetry Analysis of the Resonance Curve in Resonant Integrated Optical Gyroscopes. Sensors, 19(15), 3305. https://doi.org/10.3390/s19153305




