Single-Mode Tapered Vertical SU-8 Waveguide Fabricated by E-Beam Lithography for Analyte Sensing
Abstract
:1. Introduction
2. Structure Design and Simulation
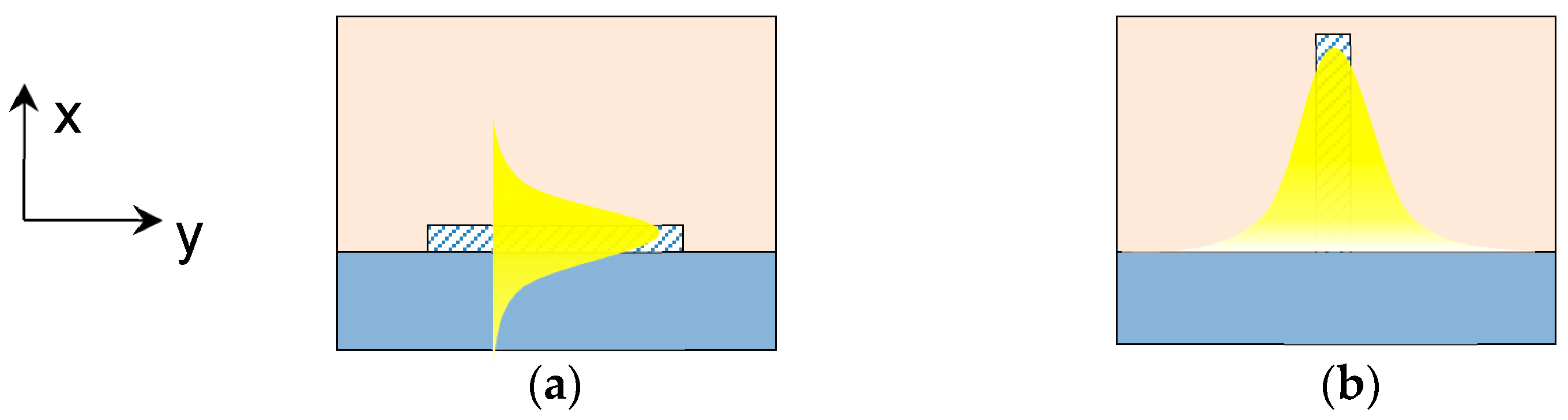
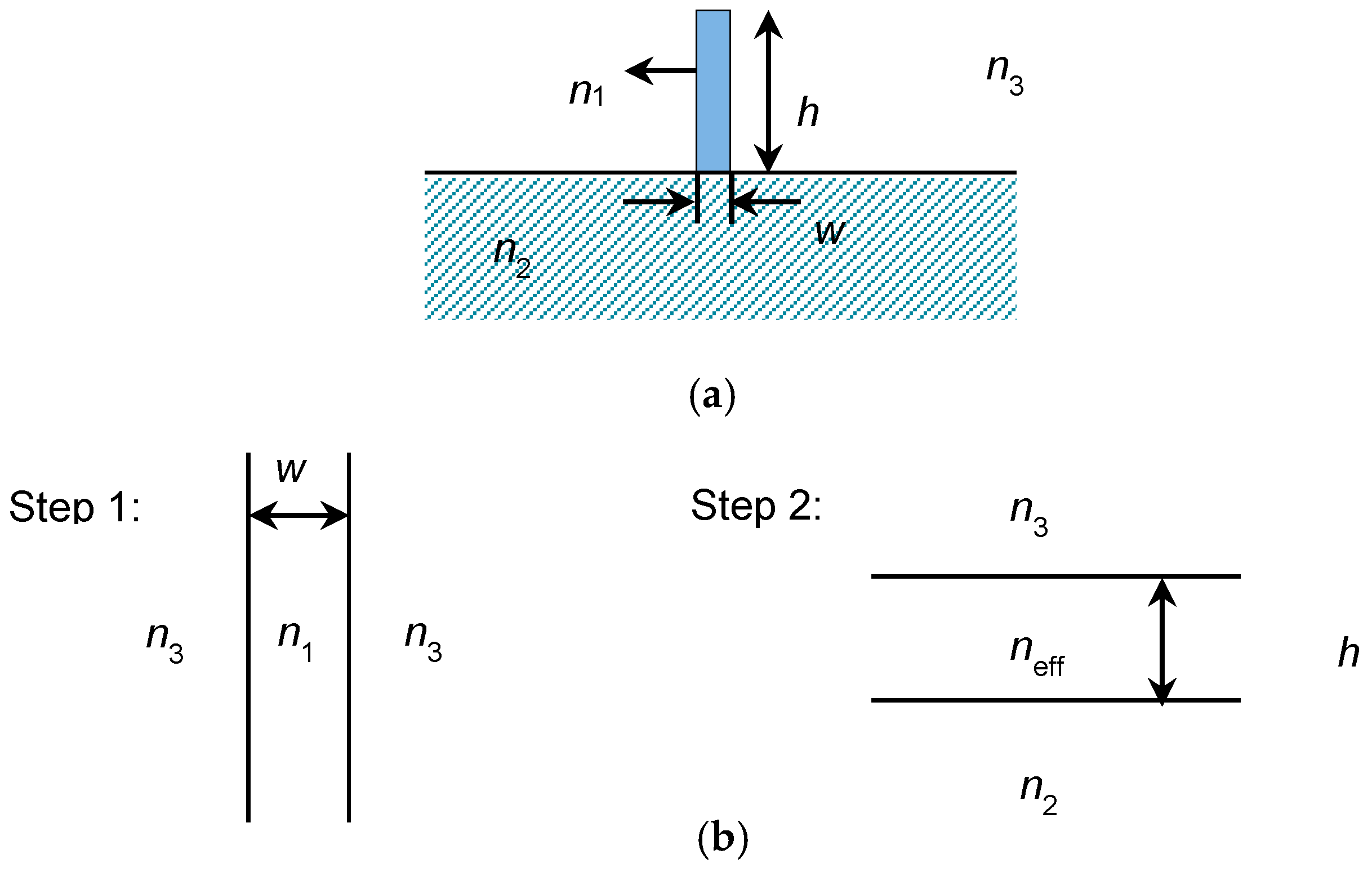
2.1. Structure Analysis
2.2. Simulations
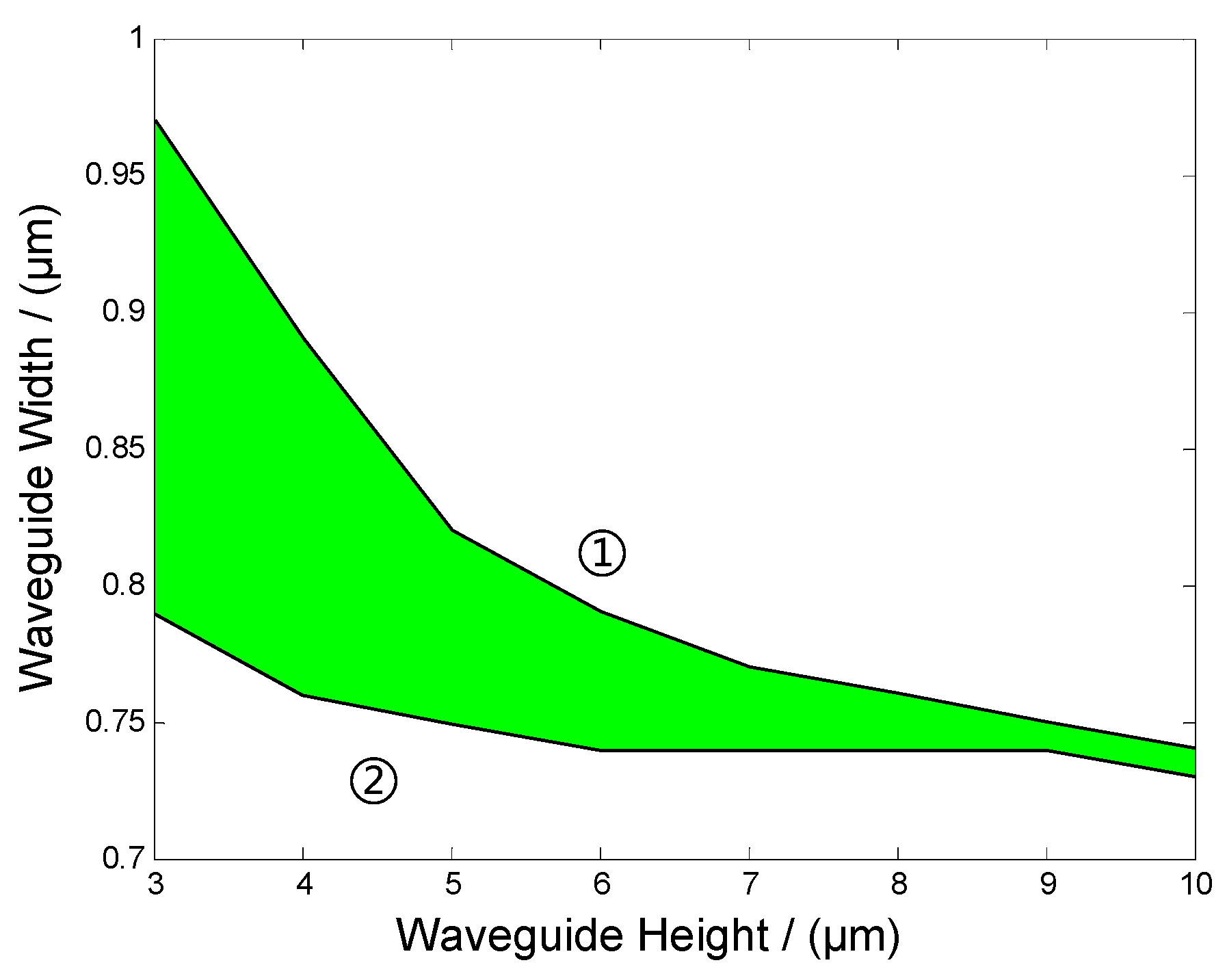
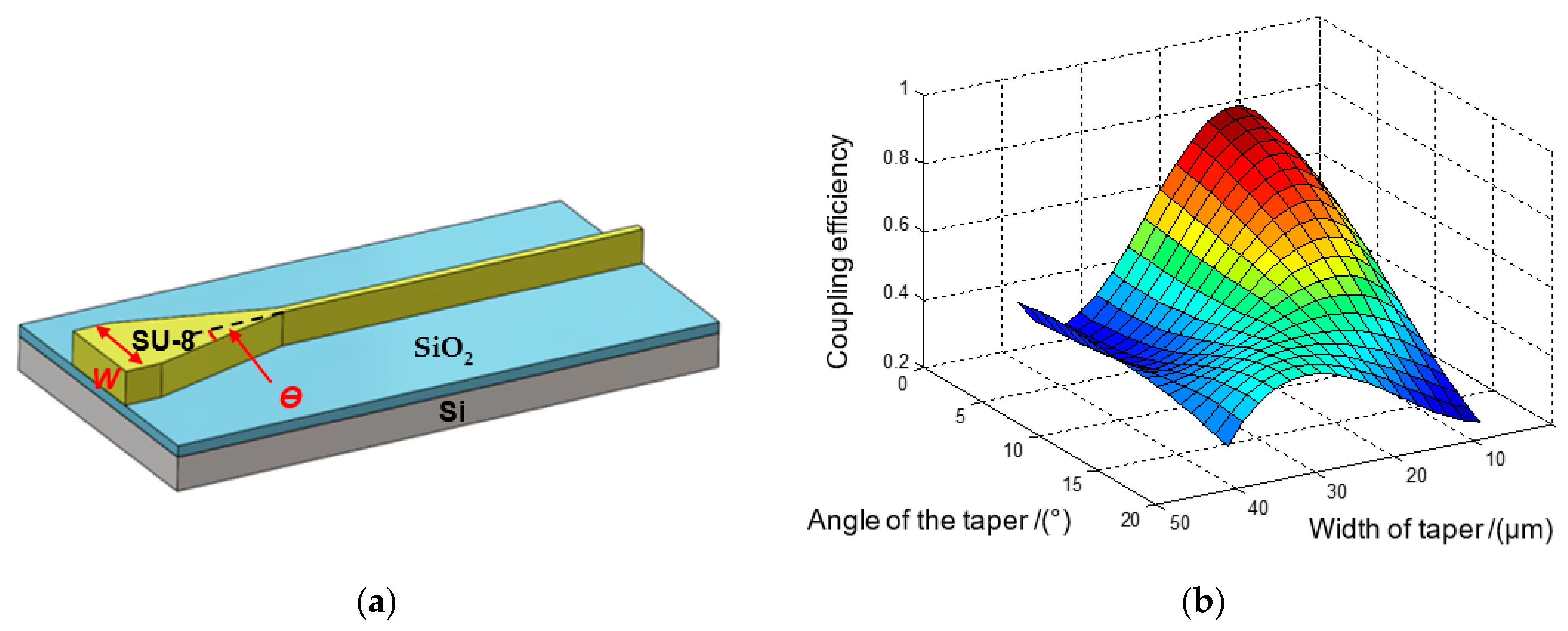
3. Taper Design and Simulation
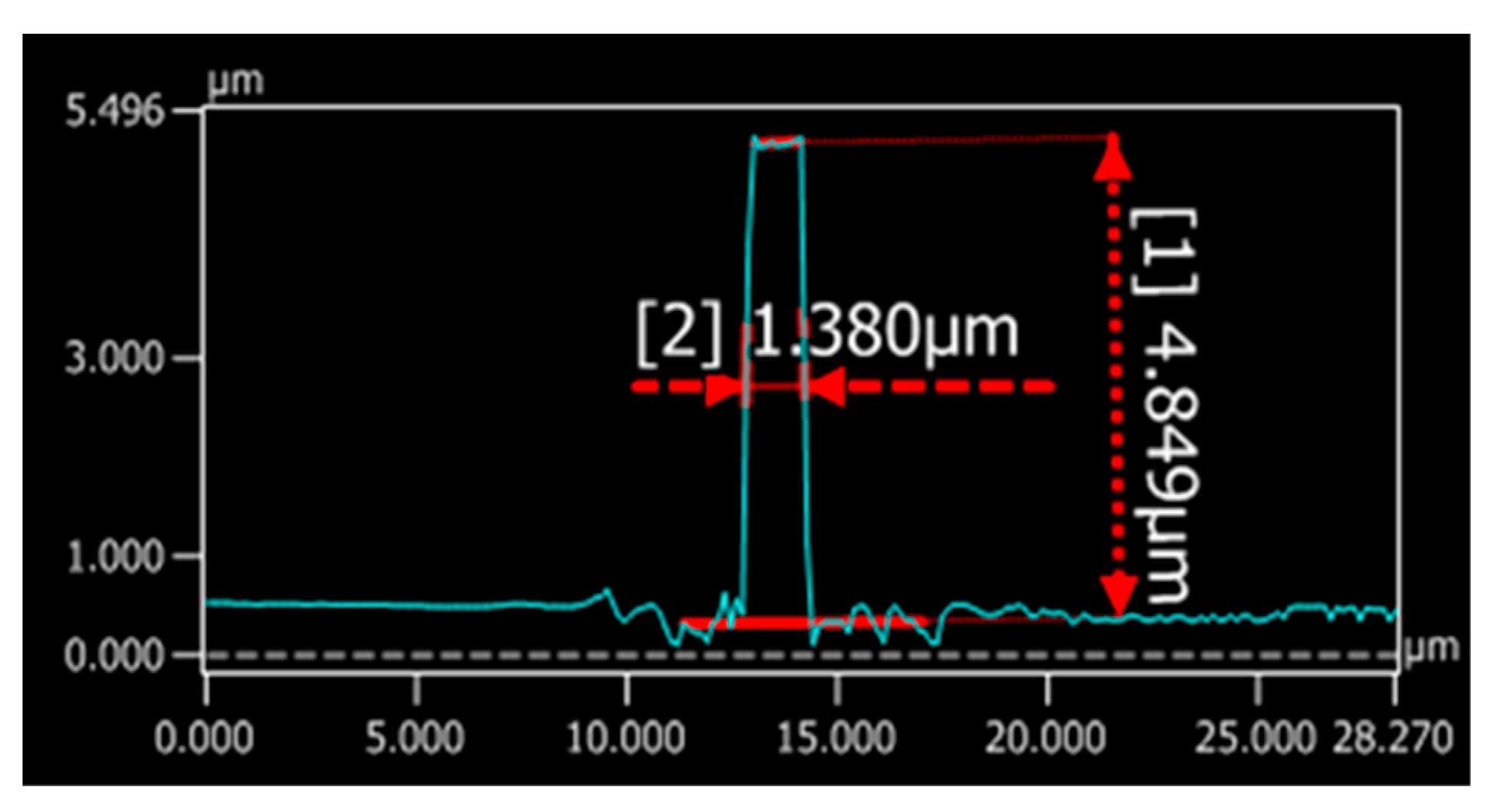
4. Fabrication
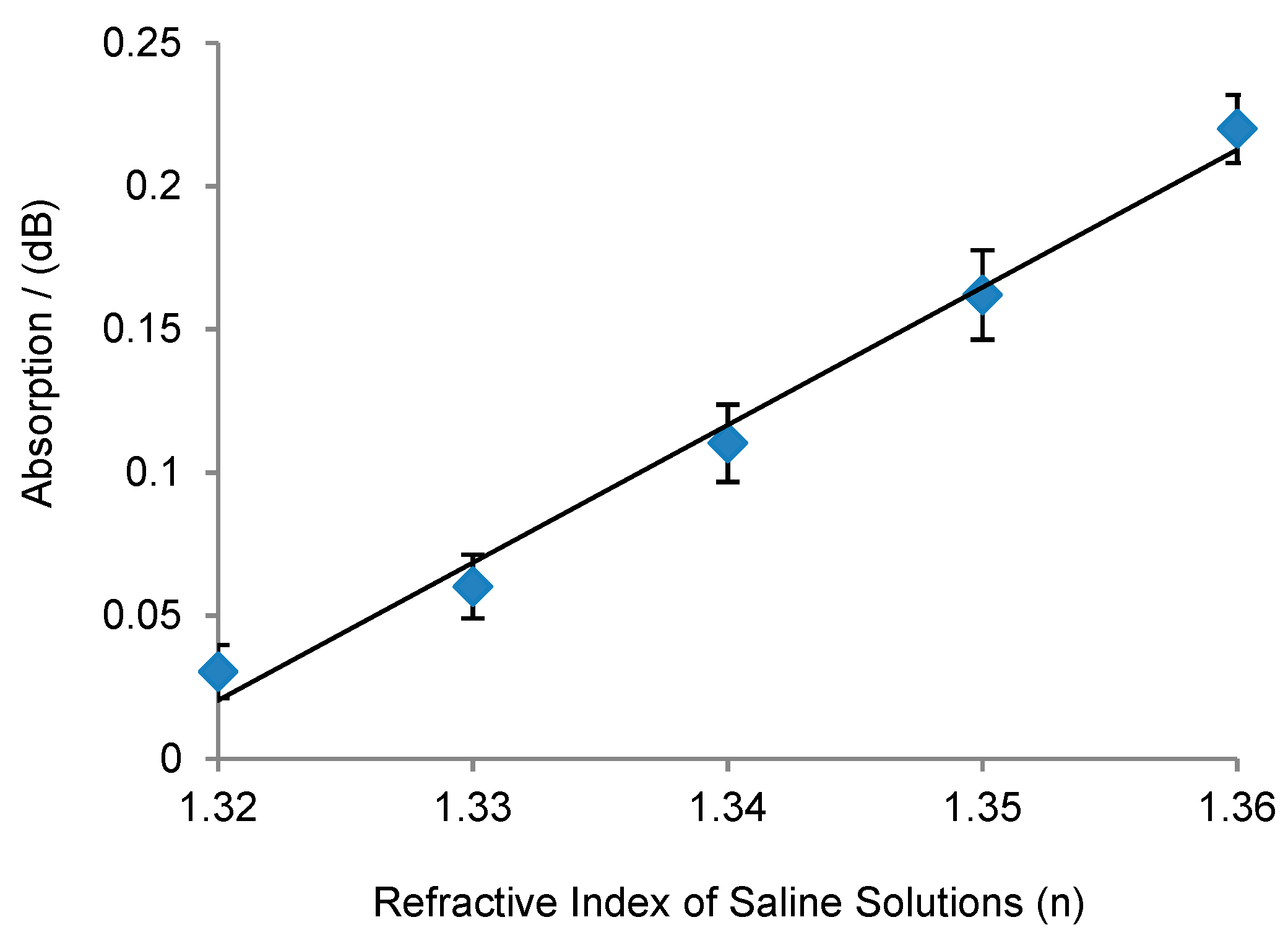
5. Measurements
- Waveguide with an adjustable platform;
- Light source: Superluminescent Light-Emitting Diodes (SLEDs): EXS1320-2111, EXALOS), the SLEDs board driver, fibers (P3-SMF28-FC-2, Thorlabs);
- Photodiode power sensors (Seri S122C, Thorlabs) and power meter (PM100D, Thorlab);
- The optical source was connected using an FC connector with single mode fibers. The Fibers were mounted onto the 3-directional adjustable platform. The transmitted optical energy was detected by the photodiode and displayed on a power meter.
6. Discussions and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Miller, S.E. Integrated optics: An Introduction. Bell Syst. Tech. J. 1969, 48, 2059–2069. [Google Scholar] [CrossRef]
- Piao, X.; Yu, S.; Park, N. Control of Fano asymmetry in plasmon induced transparency and its application to plasmonic waveguide modulator. Opt. Express 2012, 20, 18994. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.C.; Fauver, M.; Ho, J.N.; Seibel, E.J.; Reinhall, P.G. Micromachined optical waveguide cantilever as a resonant optical scanner. Sens. Actuators A Phys. 2002, 102, 165–175. [Google Scholar] [CrossRef]
- Ollier, E. Optical MEMS devices based on moving waveguides. IEEE J. Sel. Top. Quantum Electron. 2002, 8, 155–162. [Google Scholar] [CrossRef]
- Mukundan, H.; Anderson, A.S.; Grace, W.K.; Grace, K.M.; Hartman, N.; Martinez, J.S.; Swanson, B.I. Waveguide-Based Biosensors for Pathogen Detection. Sensors 2009, 9, 5783–5809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eldada, L.; Shacklette, L. Advances in polymer integrated optics. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 54–68. [Google Scholar] [CrossRef]
- Sum, T.C.; Bettiol, A.A.; Van Kan, J.A.; Watt, F.; Pun, E.Y.B.; Tung, K.K. Proton beam writing of low-loss polymer optical waveguides. Appl. Phys. Lett. 2003, 83, 1707. [Google Scholar] [CrossRef]
- Müller, R.; Cristea, D.; Kusko, M.; Obreja, P.; Damian, V.; Logofatu, P.C. SU8 polymer materials used in integrated optic microsystems. Optoelectron. Adv. Mater. Commun. 2010, 4, 228–233. [Google Scholar]
- Chronis, N.; Chronis, N.; Lee, L.P. Electrothermally Activated SU-8 Microgripper for Single Cell Manipulation in Solution. IEEE 2005, 14, 857–863. [Google Scholar] [CrossRef]
- Microchem. SU-8 3000 Permanent Epoxy Negative Photoresist. 2018. Available online: http://www.microchem.com/pdf/SU-8 3000 Data Sheet.pdf (accessed on 5 October 2017).
- Deepu, A.; Sai, V.; Mukherji, S. Simple surface modification techniques for immobilization of biomolecules on SU-8. J. Mater Sci. Mater. Med. 2009, 20, 25–28. [Google Scholar] [CrossRef] [PubMed]
- Boiragi, I.; Makkar, R.; Choudhury, B.D.; Mallik, A.; Chalapathi, K.; Sebastian, J. SU-8 Polymer Based Waveguide Biochemical Sensor for Medical Diagnostic Application. In Proceedings of the ICOP 2009-International Conference on Optics and Photonics CSIO, Chandigarh, India, 30 October–1 November 2009; pp. 2–5. [Google Scholar]
- Iizuka, K. Element of Photonics: For Fiber and Integrated Optics Volume II; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Pelletier, N.; Gaviot, E.; Zyss, J. Single-mode TE 00-TM 00 optical waveguides on SU-8 polymer. Opt. Commun. 2004, 230, 91–94. [Google Scholar]
- Marinins, A.; Knudde, N.; Popov, S. Air-suspended SU-8 strip waveguides with high refractive index contrast. IEEE Photonics Technol. Lett. 2016, 28, 1. [Google Scholar] [CrossRef]
- Nordström, M.; Zauner, D.A.; Boisen, A.; Hübner, J. Single-Mode Waveguides with SU-8 Polymer Core and Cladding for MOEMS Applications. J. Lightwave Technol. 2007, 25, 1284–1289. [Google Scholar] [CrossRef]
- Cunningham, B.T. Label-free optical biosensors: An introduction. In Label-Free Biosens: Techniques and Applications; Cambridge University Press: Cambridge, UK, 2009; pp. 1–28. [Google Scholar]
- Dell’Olio, F.; Passaro, V.M. Optical sensing by optimized silicon slot waveguides. Opt. Express 2007, 15, 4977. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Zhang, Y.; Zeng, C.; Li, D.P.; Niar, M.S.; Yu, J.Z.; Xia, J.S. High Confinement Factor Ridge Slot Waveguide for Optical Sensing. IEEE Photonics Technol. Lett. 2015, 27, 2395–2398. [Google Scholar]
- Reed, G.T.; Knight, A.P. Silicon Photonics: An Introduction; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Prabhakar, A.; Mukherji, S. Microfabricated polymer chip with integrated U-bend waveguides for evanescent field absorption based detection. Lab Chip 2010, 10, 748. [Google Scholar] [CrossRef] [PubMed]
- Pandraud, G.; French, P.; Sarro, P. Fabrication and characteristics of a PECVD SiC evanescent wave optical sensor. Sens. Actuators A Phys. 2008, 142, 61–66. [Google Scholar] [CrossRef]
- Kedenburg, S.; Vieweg, M.; Gissibl, T.; Giessen, H. Linear refractive index and absorption measurements of nonlinear optical liquids in the visible and near-infrared spectral region. Opt. Mater. Express 2012, 2, 1588. [Google Scholar] [CrossRef]
- Li, X.; Liu, L.; Zhao, J.; Tan, J. Optical Properties of Sodium Chloride Solution within the Spectral Range from 300 to 2500 nm at Room Temperature. Appl. Spectrosc. 2015, 69, 635–640. [Google Scholar] [CrossRef]
- Hunsperger, R.G. Integrated Optics; Springer: Berlin, Germany, 2009. [Google Scholar]
- Mitomi, O.; Kasaya, K.; Miyazawa, H. Design of a single-mode tapered waveguide for low-loss chip-to-fiber coupling. IEEE J. Quantum Electron. 1994, 30, 1787–1793. [Google Scholar] [CrossRef]
- Verhaar, T.M.; Wei, J.; Sarro, P.M. Pattern transfer on a vertical cavity sidewall using SU8. J. Micromechanics Microengineering 2009, 19, 74018. [Google Scholar] [CrossRef]


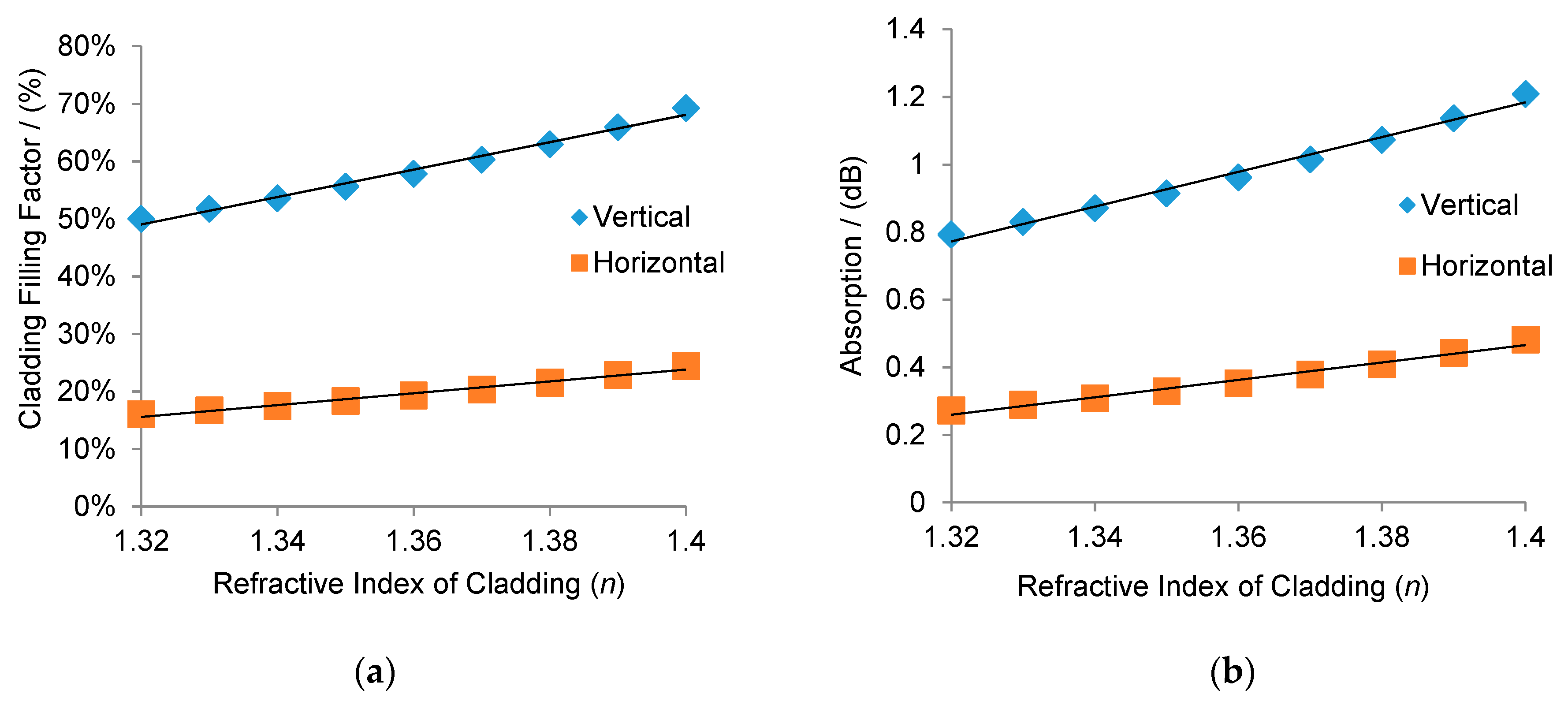





| Width | Height | Cladding Filling Factor (On Top) | Cladding Filling Factor (On Sides) | |
|---|---|---|---|---|
| Horizontal | 2 µm | 0.1 µm | 20% | 0.0015% |
| Vertical | 0.1 µm | 2 µm | 0.00127% | 46% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, Y.; Pandraud, G.; Zhang, Y.; French, P. Single-Mode Tapered Vertical SU-8 Waveguide Fabricated by E-Beam Lithography for Analyte Sensing. Sensors 2019, 19, 3383. https://doi.org/10.3390/s19153383
Xin Y, Pandraud G, Zhang Y, French P. Single-Mode Tapered Vertical SU-8 Waveguide Fabricated by E-Beam Lithography for Analyte Sensing. Sensors. 2019; 19(15):3383. https://doi.org/10.3390/s19153383
Chicago/Turabian StyleXin, Yu, Gregory Pandraud, Yongmeng Zhang, and Paddy French. 2019. "Single-Mode Tapered Vertical SU-8 Waveguide Fabricated by E-Beam Lithography for Analyte Sensing" Sensors 19, no. 15: 3383. https://doi.org/10.3390/s19153383
APA StyleXin, Y., Pandraud, G., Zhang, Y., & French, P. (2019). Single-Mode Tapered Vertical SU-8 Waveguide Fabricated by E-Beam Lithography for Analyte Sensing. Sensors, 19(15), 3383. https://doi.org/10.3390/s19153383





