New Motion Intention Acquisition Method of Lower Limb Rehabilitation Robot Based on Static Torque Sensors
Abstract
:1. Introduction
2. Materials and Methods
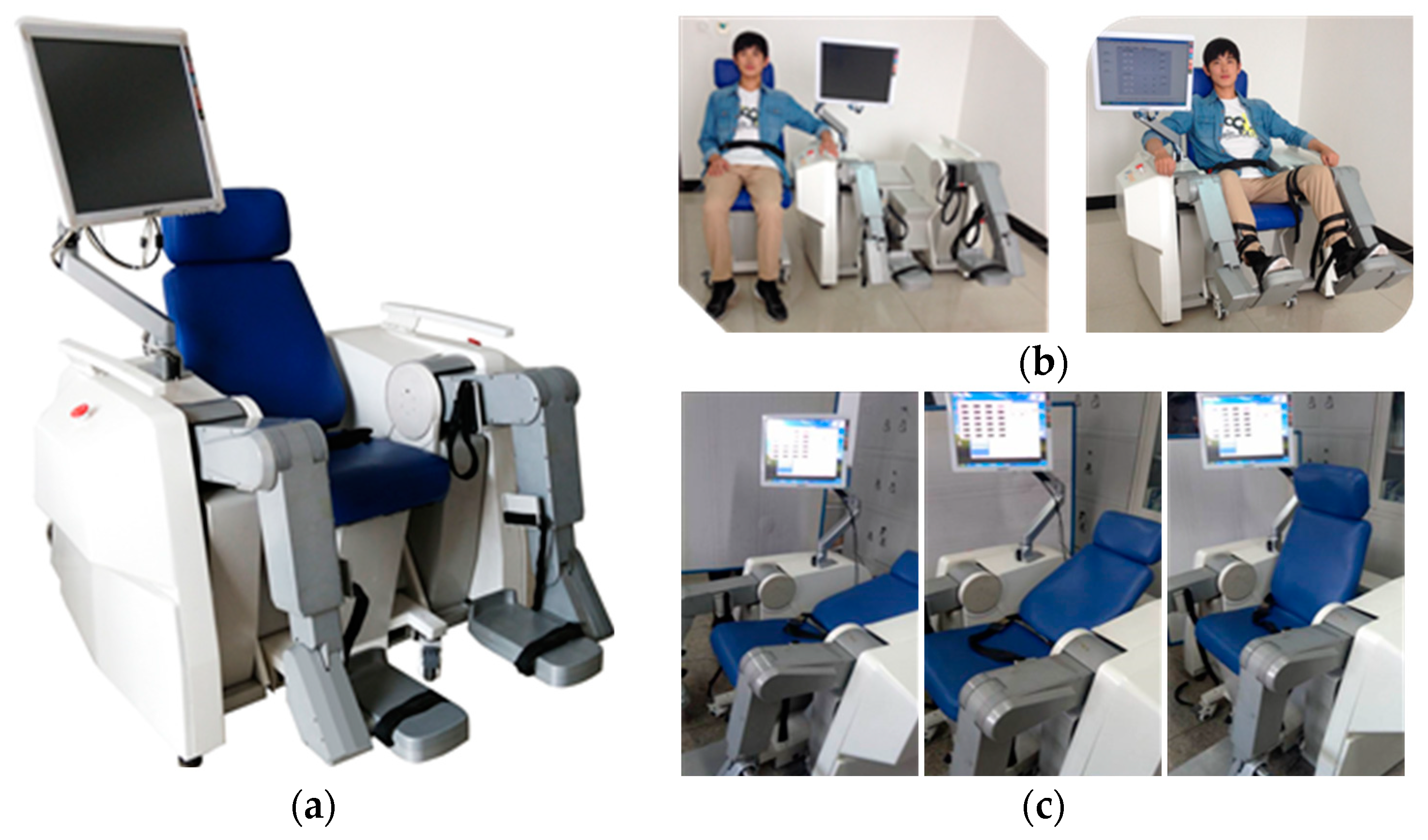
2.1. Mechanism and Hardware Control System Design of the LLR-Ro
2.2. Patient Lower Limb Motion Intention Acquisition
3. Results
3.1. Verification of the Mechanism Leg Dynamics Equations
3.2. Calibration Experiment of the Joint Static Torque Sensors
3.3. Verification Experiment of the Motion Intension Acquisition Based on Biomechanics
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shi, L.; Duan, F.; Yang, Y.; Sun, Z. The effect of treadmill walking on gait and upper trunk through linear and nonlinear analysis methods. Sensors 2019, 19, 2204. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wang, L.; Meijneke, C.; Van Asseldonk, E.; Hoellinger, T.; Cheron, G.; Ivanenko, Y.; La Scaleia, V.; Sylos-Labini, F.; Molinari, M.; et al. Design and control of the mindwalker exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Kwakkel, G.; Kollen, B.J.; van der Grond, J.; Prevo, A.J. Probability of regaining dexterity in the flaccid upper limb: Impact of severity of paresis and time since onset in acute stroke. Stroke 2003, 34, 2181–2186. [Google Scholar] [CrossRef] [PubMed]
- Koceska, N.; Koceski, S.; Durante, F.; Zobel, P.B.; Raparelli, T. Control architecture of a 10 dof lower limbs exoskeleton for gait rehabilitation. Int. J. Adv. Robot. Syst. 2013, 10, 68. [Google Scholar] [CrossRef]
- Veneman, J.F.; Kruidhof, R.; Hekman, E.E.; Ekkelenkamp, R.; Van Asseldonk, E.H.; Van Der Kooij, H. Design and evaluation of the lopes exoskeleton robot for interactive gait rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 379–386. [Google Scholar] [CrossRef] [PubMed]
- Iñaki, D.; Gil, J.J.; Emilio, S. Lower-limb robotic rehabilitation: Literature review and challenges. Int. J. Robot. 2011, 1–11. [Google Scholar] [CrossRef]
- Meng, W.; Liu, Q.; Zhou, Z.D.; Ai, Q.S. Recent development of mechanisms and control strategies for robot-assisted lower limb rehabilitation. Mechatronics 2015, 31, 132–145. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, Y.; Yi, J.; Liu, T. An integrated hysical-learning model of physical human-robot interactions with application to pose estimation in bikebot riding. Int. J. Robot. Res. 2016, 35, 1459–1476. [Google Scholar] [CrossRef]
- Gan, D.; Qiu, S.; Guan, Z.; Shi, C.; Li, Z. Development of an exoskeleton robot for lower limb rehabilitation. In Proceedings of the Conference on Advanced Robotics and Mechatronics, Macau, China, 18–20 August 2016; pp. 312–317. [Google Scholar] [CrossRef]
- Esquenazi, A.; Talaty, M.; Packel, A.; Saulino, M. The rewalk powered exoskeleton to restore ambulatory function to individuals with thoracic-level motor-complete spinal cord injury. Am. J. Phys. Med. Rehabil. 2012, 91, 911–921. [Google Scholar] [CrossRef]
- Fleerkotte, B.M.; Koopman, B.; Buurke, J.H.; van Asseldonk, E.H.; van der Kooij, H.; Rietman, J.S. The effect of impedance-controlled robotic gait training on walking ability and quality in individuals with chronic incomplete spinal cord injury: An explorative study. J. Neuroeng. Rehabil. 2014, 11, 498–500. [Google Scholar] [CrossRef]
- Meuleman, J.; van Asseldonk, E.; van Oort, G.; Rietman, H.; van der Kooij, H. LOPES II—Design and evaluation of an admittance controlled gait training robot with shadow-leg approach. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 352–363. [Google Scholar] [CrossRef] [PubMed]
- Koenig, A.; Riener, R. The human in the loop. In Neurorehabilitation Technology; Reinkensmeyer, D.J., Ed.; Springer-Verlag: London, UK, 2016; pp. 161–181. [Google Scholar]
- Alcobendas-Maestro, M.; Esclarín-Ruz, A.; Casado-López, R.M.; Muñoz-González, A.; Perez-Mateos, G.; Gonzalez-Valdizan, E.; Martin, J.L. Lokomat robotic-assisted versus overground training within 3 to 6 months of incomplete spinal cord lesion: Randomized controlled trial. J. Neuroeng. Rehabil. 2012, 26, 1058–1063. [Google Scholar] [CrossRef] [PubMed]
- Patrick, M.; Mohamed, B. Improvement of rehabilitation possibilities with the motionmaker TM. In Proceedings of the 1st IEEE/RAS-EMBS International Conf. on Biomedical Robotics and Biomechatronics, Pisa, Italy, 20–22 February 2006; pp. 359–364. [Google Scholar] [CrossRef]
- Wang, H.; Shi, X.; Liu, H.; Li, L.; Hou, Z.; Yu, H. Design, Kinematics, Simulation and Experiment for a Lower Limb Rehabilitation Robot. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2011, 225, 860–872. [Google Scholar] [CrossRef]
- Mayr, A.; Quirbach, E.; Picelli, A.; Kofler, M.; Smania, N.; Saltuari, L. Early robot-assisted gait retraining in non-ambulatory patients with stroke: A single blind randomized controlled trial. Eur. J. Phys. Rehabil. Med. 2018, 54, 819–826. [Google Scholar] [CrossRef] [PubMed]
- Aurich-Schuler, T.; Gut, A.; Labruyere, R. The freed module for the lokomat facilitates a physiological movement pattern in healthy people—A proof of concept study. J. Neuroeng. Rehabil. 2019, 16, 1–13. [Google Scholar] [CrossRef]
- Bouri, M.; Gall, B.L.; Clavel, R. A new concept of parallel robot for rehabilitation and fitness: The lambda. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Guilin, China, 12–23 December 2009; IEEE: New York, NY, USA, 2009; pp. 2503–2508. [Google Scholar] [CrossRef]
- Chisholm, K.J.; Klumper, K.; Mullins, A.; Ahmadi, M. A task oriented haptic gait rehabilitation robot. Mechatronics 2014, 24, 1083–1091. [Google Scholar] [CrossRef]
- Akdogan, E.; Adli, M.A. The design and control of a therapeutic exercise robot for lower limb rehabilitation: Physiotherabot. Mechatronics 2011, 21, 509–522. [Google Scholar] [CrossRef]
- Srivastava, S.; Kao, P.; Kim, S.; Stegall, P. Assist-as-needed robot-aided gait training improves walking function in individuals. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 23, 956–963. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, D.; Lu, H.; Feng, Y.; Xu, P.; Mihai, R.V.; Vladareanu, L. Active training research of a lower limb rehabilitation robot based on constrained trajectory. In Proceedings of the International Conf. on Advanced Mechatronic Systems, Beijing, China, 22–24 August 2015; pp. 24–29. [Google Scholar] [CrossRef]
- Hussain, S.; Xie, S.Q.; Jamwal, P.K. Adaptive impedance control of a robotic orthosis for gait rehabilitation. IEEE Trans. Cybernet. 2013, 43, 1025–1034. [Google Scholar] [CrossRef]
- Hussian, S.; Jamwai, P.K.; Ghayesh, M.H.; Xie, S.Q. Assist-as-needed control of an intrinsically compliant robotic gait training orthosis. IEEE Trans. Ind. Electron. 2016, 99, 1–10. [Google Scholar] [CrossRef]
- Zhang, F.; Hou, Z.G.; Cheng, L.; Wang, W.; Chen, Y.; Hu, J.; Peng, L.; Wang, H. iLeg—A lower limb rehabilitation robot: A proof of concept. IEEE Trans. Hum.-Mach. Syst. 2016, 46, 761–768. [Google Scholar] [CrossRef]
- Leonardis, D.; Barsotti, M.; Loconsole, C.; Solazzi, M.; Troncossi, M.; Mazzotti, C.; Castelli, V.P.; Procopio, C.; Lamola, G.; Chisari, C.; et al. An EMG-controlled robotic hand exoskeleton for bilateral rehabilitation. IEEE Trans. Haptics 2015, 8, 140–151. [Google Scholar] [CrossRef] [PubMed]
- Yepes, J.C.; Portela, M.A.; Saldarriaga, Á.J.; Pérez, V.Z.; Betancur, M.J. Myoelectric control algorithm for robot-assisted therapy: A hardware-in-the-loop simulation study. Biomed. Eng. Online 2019, 18, 3. [Google Scholar] [CrossRef] [PubMed]
- Khoshdel, V.; Akbarzadeh, A.; Naghavi, N.; Sharifnezhad, A.; Souzanchi-Kashani, M. sEMG-based impedance control for lower-limb rehabilitation robot. Intell. Serv. Robot. 2017, 11, 97–108. [Google Scholar] [CrossRef]
- Wittmann, F.; Lambercy, O.; Gassert, R. Magnettometer-based drift correction during rest in IMU arm motion tracking. Sensors 2019, 19, 1312. [Google Scholar] [CrossRef] [PubMed]
- Riener, R.; Koenig, A.; Bolliger, M.; Wieser, M.; Duschau-Wicke, A.; Vallery, H. Bio-cooperative robotics: Controlling mechanical, physiological and mental patient states. In Proceedings of the IEEE International Conference on Rehabilitation Robotics, Tokyo, Japan, 23–26 June 2009; pp. 407–412. [Google Scholar] [CrossRef]
- Wang, X.; Lu, T.; Wang, S.; Gu, J.; Yuan, K. A patient-driven control method for lower-limb rehabilitation robot. In Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016; pp. 908–913. [Google Scholar] [CrossRef]
- Hwang, B.; Jeon, D. Estimation of the user’s muscular torque for an over-ground gait rehabilitation robot using torque and insole pressure sensors. Int. J. Control Autom. 2018, 16, 275–283. [Google Scholar] [CrossRef]
- Alia, C.; Spalletti, C.; Lai, S.; Panarese, A.; Lamola, G.; Bertolucci, F.; Vallone, F.; Di Garbo, A.; Chisari, C.; Micera, S.; et al. Neuroplastic changes following brain ischemia and their contribution to stroke recovery: Novel approaches in neurorehabilitation. Front. Cell. Neurosci. 2017, 11, 76. [Google Scholar] [CrossRef] [PubMed]
- Craig, J.J. Introduction to Robotics, 3rd ed.; Pearson Education International: Upper Saddle River, NJ, USA, 2005; pp. 201–316. [Google Scholar]













| Parameters | Thigh | Calf | Foot |
|---|---|---|---|
| Segment Length | 390 mm | 400 mm | 100 mm |
| Distance from Centroid to the Joint Axis | 50 mm | 250 mm | 50 mm |
| Segment Rotational Intertia | 1.5 kg·m2 | 0.2 kg·m2 | 0.02 kg·m2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Wang, H.; Vladareanu, L.; Chen, Z.; Jin, D. New Motion Intention Acquisition Method of Lower Limb Rehabilitation Robot Based on Static Torque Sensors. Sensors 2019, 19, 3439. https://doi.org/10.3390/s19153439
Feng Y, Wang H, Vladareanu L, Chen Z, Jin D. New Motion Intention Acquisition Method of Lower Limb Rehabilitation Robot Based on Static Torque Sensors. Sensors. 2019; 19(15):3439. https://doi.org/10.3390/s19153439
Chicago/Turabian StyleFeng, Yongfei, Hongbo Wang, Luige Vladareanu, Zheming Chen, and Di Jin. 2019. "New Motion Intention Acquisition Method of Lower Limb Rehabilitation Robot Based on Static Torque Sensors" Sensors 19, no. 15: 3439. https://doi.org/10.3390/s19153439
APA StyleFeng, Y., Wang, H., Vladareanu, L., Chen, Z., & Jin, D. (2019). New Motion Intention Acquisition Method of Lower Limb Rehabilitation Robot Based on Static Torque Sensors. Sensors, 19(15), 3439. https://doi.org/10.3390/s19153439






