People Counting by Dense WiFi MIMO Networks: Channel Features and Machine Learning Algorithms †
Abstract
:1. Introduction
Contributions
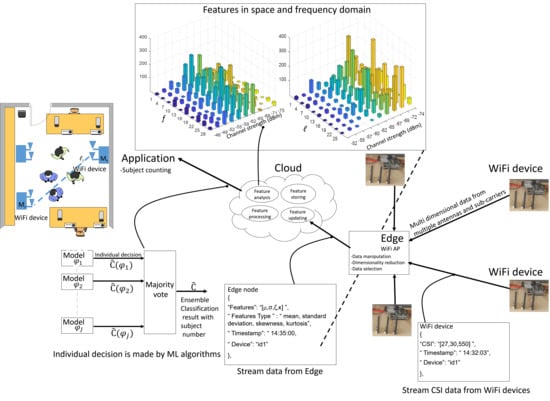
2. CSI Features for Subject Counting
2.1. MIMO-OFDM Channel Response and CSI Data Sets
2.2. Space-Frequency Domain CSI Features
3. Computing Architecture and Processing Tools for Subject Counting
3.1. Machine Learning Tools for CSI Feature Processing
3.2. Kullback-Leibler Divergence for Processing of CSI Distribution Features
4. Subject Counting: Results and Discussions
4.1. Classifier tools for Subject Counting
4.2. Ensemble Learning and Bagging: Channel Features and Comparative Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sigg, S.; Scholz, M.; Shi, S.; Ji, Y.; Beigl, M. RF-Sensing of Activities from Non-Cooperative Subjects in Device-Free Recognition Systems Using Ambient and Local Signals. IEEE Trans. Mob. Comput. 2014, 13, 907–920. [Google Scholar] [CrossRef]
- Witrisal, K.; Meissner, P.; Leitinger, E.; Shen, Y.; Gustafson, C.; Tufvesson, F.; Haneda, K.; Dardari, D.; Molisch, A.F.; Conti, A.; et al. High-Accuracy Localization for Assisted Living: 5G systems will turn multipath channels from foe to friend. IEEE Signal Process. Mag. 2016, 33, 59–70. [Google Scholar] [CrossRef]
- Kianoush, S.; Savazzi, S.; Vicentini, F.; Rampa, V.; Giussani, M. Device-free RF human body fall detection and localization in industrial workplaces. IEEE Internet Things J. 2016, 4, 351–362. [Google Scholar] [CrossRef]
- Bartoletti, S.; Conti, A.; Win, M.Z. Device-Free Counting via Wideband Signals. IEEE J. Sel. Areas Commun. 2017, 35, 1163–1174. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, K.; Ni, L.M. Wifall: Device-free fall detection by wireless networks. IEEE Trans. Mob. Comput. 2016, 16, 581–594. [Google Scholar] [CrossRef]
- Fadhlullah, S.Y.; Ismail, W. A Statistical Approach in Designing an RF-Based Human Crowd Density Estimation System. Int. J. Distrib. Sens. Netw. 2016, 12, 8351017. [Google Scholar] [CrossRef]
- Xu, C.; Firner, B.; Moore, R.S.; Zhang, Y.; Trappe, W.; Howard, R.; Zhang, F.; An, N. SCPL: Indoor device-free multi-subject counting and localization using radio signal strength. In Proceedings of the IEEE International Conference on Information Processing in Sensor Networks (IPSN), Philadelphia, PA, USA, 8–11 April 2013. [Google Scholar]
- Cheng, Y.K.; Chang, R.Y. Device-Free Indoor People Counting Using Wi-Fi Channel State Information for Internet of Things. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Singapore, 4–8 December 2017. [Google Scholar]
- Choi, J.W.; Quan, X.; Cho, S.H. Bi-Directional Passing People Counting System Based on IR-UWB Radar Sensors. IEEE Internet Things J. 2017, 5, 512–522. [Google Scholar] [CrossRef]
- Zazo, R.; Nidadavolu, P.S.; Chen, N.; Gonzalez-Rodriguez, J.; Dehak, N. Age Estimation in Short Speech Utterances Based on LSTM Recurrent Neural Networks. IEEE Access 2018, 6, 22524–22530. [Google Scholar] [CrossRef]
- Maeda, K. Performance evaluation of object serialization libraries in XML, JSON and binary formats. In Proceedings of the Digital Information and Communication Technology and It’s Applications (DICTAP), Bangkok, Thailand, 16–18 May 2012; pp. 177–182. [Google Scholar]
- Cicerone, M.; Simeone, O.; Spagnolini, U. Channel Estimation for MIMO-OFDM Systems by Modal Analysis/Filtering. IEEE Trans. Commun. 2006, 54, 2062–2074. [Google Scholar] [CrossRef]
- ISO/IEC 20922:2016 Information Technology—Message Queuing Telemetry Transport (MQTT) v3.1.1; International Organization for Standardization, 2016; Available online: https://www.iso.org/standard/69466.html (accessed on 5 August 2019).
- Kianoush, S.; Raja, M.; Savazzi, S.; Sigg, S. A cloud-IoT platform for passive radio sensing: Challenges and application case studies. IEEE Internet Things J. 2018, 5, 3624–3636. [Google Scholar] [CrossRef]
- Barbarossa, S.; Sardellitti, S.; Di Lorenzo, P. Communicating while computing: Distributed mobile cloud computing over 5G heterogeneous networks. IEEE Signal Process. Mag. 2014, 31, 45–55. [Google Scholar] [CrossRef]
- Hong, M.; Razaviyayn, M.; Luo, Z.Q.; Pang, J.S. A Unified Algorithmic Framework for Block-Structured Optimization Involving Big Data: With applications in machine learning and signal processing. IEEE Signal Process. Mag. 2016, 33, 57–77. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Islam, M.M.; Yao, X.; Nirjon, S.S.; Islam, M.A.; Murase, K. Bagging and Boosting Negatively Correlated Neural Networks. IEEE Trans. Syst. Man Cybern. 2008, 38, 771–874. [Google Scholar] [CrossRef] [PubMed]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef] [Green Version]
- Depatla, S.; Muralidharan, A.; Mostofi, Y. Occupancy estimation using only wifi power measurements. IEEE J. Sel. Areas Commun. 2015, 33, 1381–1393. [Google Scholar] [CrossRef]
- Kianoush, S.; Rampa, V.; Savazzi, S.; Nicoli, M. Pre-deployment performance assessment of device-free radio localization systems. In Proceedings of the 2016 IEEE International Conference on Communications Workshops (ICC’16), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 1–6. [Google Scholar]
- Omar, H.A.; Abboud, K.; Cheng, N.; Malekshan, K.R.; Gamage, A.T.; Zhuang, W. A Survey on High Efficiency Wireless Local Area Networks: Next Generation WiFi. IEEE Commun. Surv. Tutor. 2016, 18, 2315–2344. [Google Scholar] [CrossRef]
- Bahai, A.R.S.; Saltzberg, B.R.; Ergen, M. Multi-Carrier Digital Communications: Theory and Applications of OFDM, 2nd ed.; Springer: New York, NY, USA, 2004. [Google Scholar] [CrossRef]
- Kianoush, S.; Savazzi, S.; Rampa, V. Tracking of frequency selectivity for device-free detection of multiple targets. In Proceedings of the 2017 IEEE International Conference on Communications (ICC’2017), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]










| C | Empty | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| space domain | 0.44 | 1 | 0.84 | 0.9 | 0.43 | 0.55 |
| frequency domain | 1 | 0.9 | 0.92 | 0.31 | 0.54 | 0.3 |
| C | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| space domain | 1 | 0.51 | 0.43 | 0.29 | 0.22 |
| frequency domain | 0.93 | 0.5 | 0.4 | 0.39 | 0.28 |
| FF-NN, Frequency Domain | ||||||
| C | Empty | 1 | 2 | 3 | 4 | 5 |
| kurtosis | 0.24 | 0.21 | 0.68 | 0.36 | 0.42 | 0.557 |
| skewness | 0.45 | 0.956 | 0.63 | 0.7 | 0.59 | 0.52 |
| standard deviation | 0.68 | 0.78 | 0.84 | 0.67 | 0.58 | 0.76 |
| mean | 0.73 | 0.9 | 0.94 | 0.79 | 0.67 | 0.84 |
| FF-NN, Space Domain | ||||||
| C | Empty | 1 | 2 | 3 | 4 | 5 |
| kurtosis | 0.31 | 0.43 | 0.61 | 0.46 | 0.43 | 0.47 |
| skewness | 0.29 | 0.46 | 0.54 | 0.36 | 0.54 | 0.62 |
| standard deviation | 0.43 | 0.65 | 0.89 | 0.63 | 0.71 | 0.78 |
| mean | 0.92 | 0.96 | 0.98 | 0.94 | 0.96 | 0.92 |
| LSTM, Frequency Domain | ||||||
| C | Empty | 1 | 2 | 3 | 4 | 5 |
| kurtosis | 1 | 1 | 0.9 | 0.36 | 0.63 | 0.45 |
| skewness | 1 | 0.9 | 1 | 0.9 | 0.27 | 0.45 |
| standard deviation | 0.18 | 1 | 1 | 0.81 | 0.72 | 0.9 |
| mean | 0.72 | 0.45 | 1 | 0.8 | 1 | 1 |
| LSTM, Space Domain | ||||||
| C | Empty | 1 | 2 | 3 | 4 | 5 |
| kurtosis | 1 | 0.9 | 1 | 0.63 | 0.72 | 0.36 |
| skewness | 1 | 1 | 1 | 0.72 | 0.63 | 0.54 |
| standard deviation | 0.8 | 1 | 1 | 1 | 1 | 1 |
| mean | 1 | 1 | 1 | 0.9 | 1 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kianoush, S.; Savazzi, S.; Rampa, V.; Nicoli, M. People Counting by Dense WiFi MIMO Networks: Channel Features and Machine Learning Algorithms. Sensors 2019, 19, 3450. https://doi.org/10.3390/s19163450
Kianoush S, Savazzi S, Rampa V, Nicoli M. People Counting by Dense WiFi MIMO Networks: Channel Features and Machine Learning Algorithms. Sensors. 2019; 19(16):3450. https://doi.org/10.3390/s19163450
Chicago/Turabian StyleKianoush, Sanaz, Stefano Savazzi, Vittorio Rampa, and Monica Nicoli. 2019. "People Counting by Dense WiFi MIMO Networks: Channel Features and Machine Learning Algorithms" Sensors 19, no. 16: 3450. https://doi.org/10.3390/s19163450
APA StyleKianoush, S., Savazzi, S., Rampa, V., & Nicoli, M. (2019). People Counting by Dense WiFi MIMO Networks: Channel Features and Machine Learning Algorithms. Sensors, 19(16), 3450. https://doi.org/10.3390/s19163450