Comparative Performance of Four Electrodes for Measuring the Electromechanical Response of Self-Damage Detecting Concrete under Tensile Load
Abstract
1. Introduction
2. Current Electrodes
2.1. Embedded-Type Electrodes
2.2. Attached-Type Electrodes
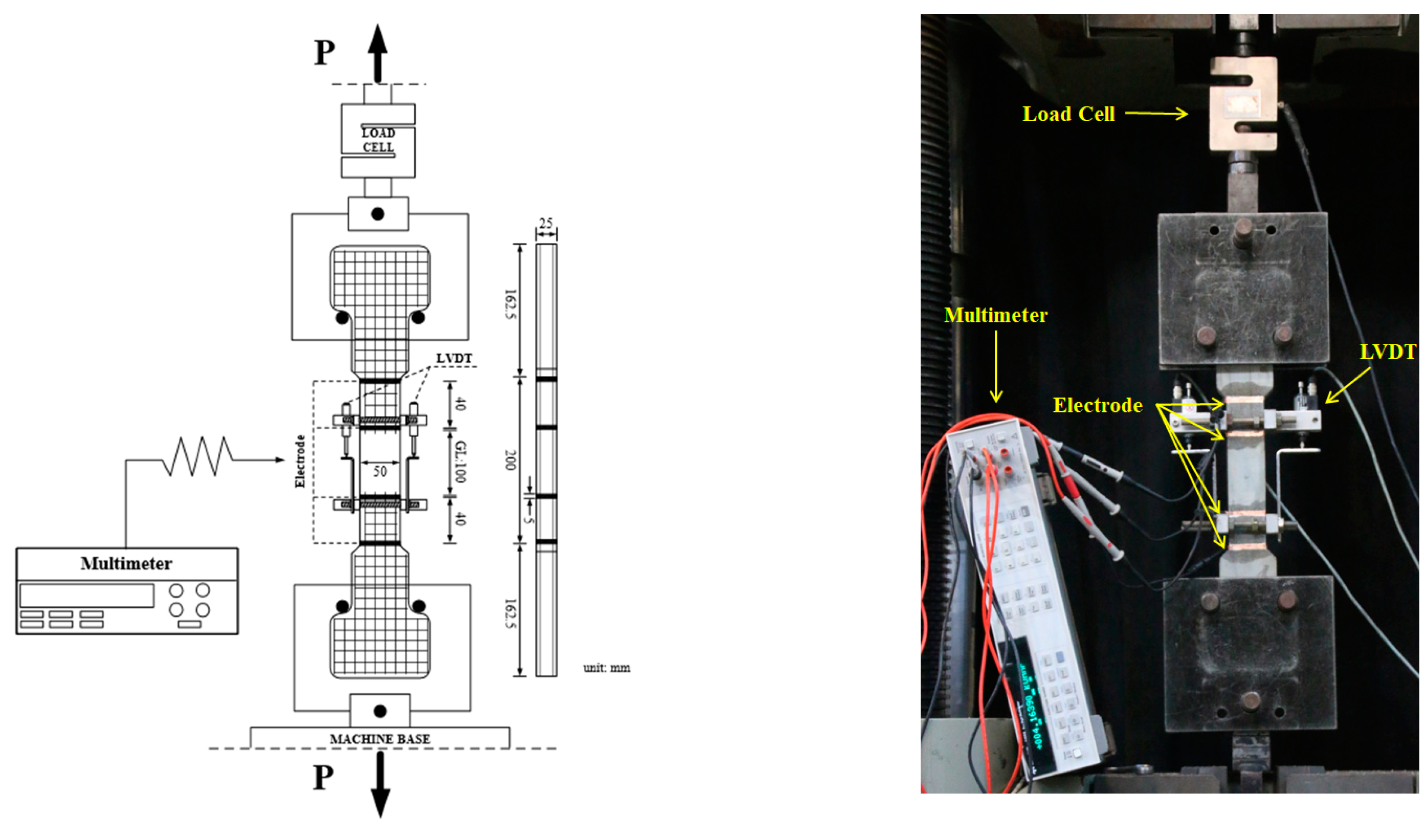
3. Experimental
3.1. Materials and Specimen Preparation
3.2. Test Set-Up and Procedure
4. Results and Discussion
4.1. Effects of Different Electrodes on the Polarization Parameters
4.2. Effects of Electrode Types on Electromechanical Response
5. Conclusions
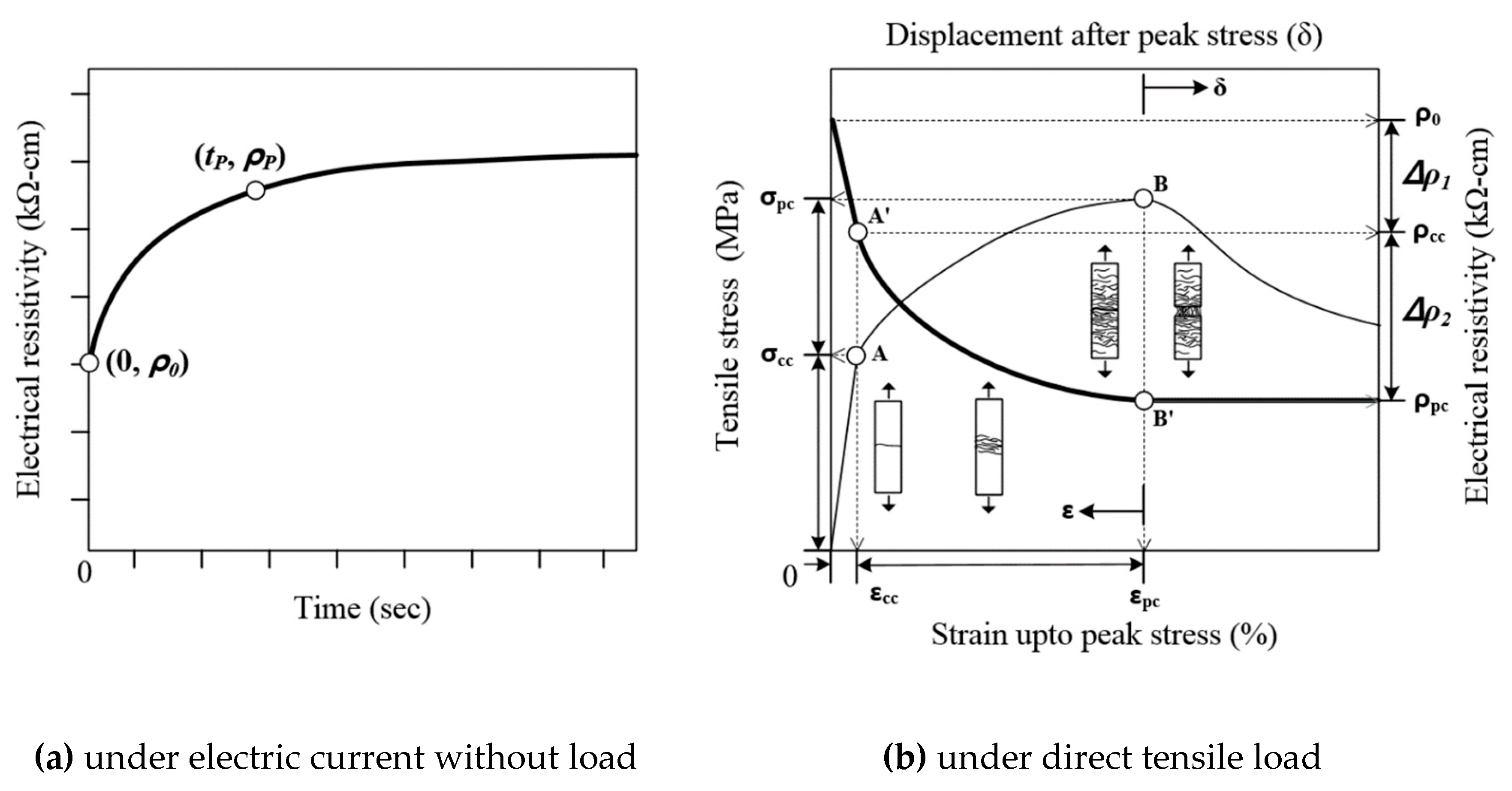
- Both the CC1 and CS electrodes produced a relatively shorter polarization time than the other electrodes (CC2 and WC2). The polarization times (tp) for the specimens using the CS and CC1 electrodes were 25 s and 80 s, respectively.
- The tp was significantly affected by the accumulation of electrons at the interface between the specimen and electrode. Higher levels of electron accumulation resulted in longer polarization times.
- The overall change in the electrical resistivity (∆ρ) upon damage to specimens equipped with the CS and CC1 electrodes was 5.3 kΩ·cm and 4.9 kΩ·cm, respectively. The CS-equipped HPFRCCs showed a higher damage-sensing capacity (GF2), whereas the CC1-equipped HPFRCCs exhibited a higher strain-sensing capacity (GF1), as well as good damage-sensing capacity.
- The CC1 electrode using copper film with type 1 carbon tape is identified as the best suited for use as a replacement for the conventional copper tape with silver paste (CS) electrode in measuring the electromechanical response of self-damage-detecting concrete.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, D.Y.; Banerjee, S.; Wang, Y.B.; Huang, S.F.; Cheng, X. Temperature and loading effects of embedded smart piezoelectric sensor for health monitoring of concrete structures. Constr. Build. Mater. 2015, 76, 187–193. [Google Scholar] [CrossRef]
- Perry, M.; Saafi, M.; Fusiek, G.; Niewczas, P. Hybrid optical-fibre/geopolymer sensors for structural health monitoring of concrete structures. Smart Mater. Struct. 2015, 24, 045011. [Google Scholar] [CrossRef]
- Li, W.J.; Kong, Q.Z.; Ho, S.C.M.; Lim, I.; Mo, Y.L.; Song, G.B. Feasibility study of using smart aggregates as embedded acoustic emission sensors for health monitoring of concrete structures. Smart Mater. Struct. 2016, 25, 115031. [Google Scholar] [CrossRef]
- Morsy, R.; Marzouk, H.; Haddara, M.; Gu, X. Multi-channel random decrement smart sensing system for concrete bridge girders damage location identification. Eng. Struct. 2017, 143, 469–476. [Google Scholar] [CrossRef]
- Yazdizadeh, Z.; Marzouk, H.; Hadianfard, M.A. Monitoring of concrete shrinkage and creep using Fiber Bragg Grating sensors. Constr. Build. Mater. 2017, 137, 505–512. [Google Scholar] [CrossRef]
- Liu, P.; Wang, W.; Chen, Y.; Feng, X.; Miao, L.X. Concrete damage diagnosis using electromechanical impedance technique. Constr. Build. Mater. 2017, 136, 450–455. [Google Scholar] [CrossRef]
- Banthia, N.; Djeridane, S.; Pigeon, M. Electrical resistivity of carbon and steel micro-fiber reinforced cements. Cem. Concr. Res. 1992, 22, 804–814. [Google Scholar] [CrossRef]
- Fu, X.; Lu, W.; Chung, D.D.L. Improving the strain-sensing ability of carbon fiber-reinforced cement by ozone treatment of the fibers. Cem. Concr. Res. 1998, 28, 183–187. [Google Scholar] [CrossRef]
- Bontea, D.M.; Chung, D.D.L.; Lee, G.C. Damage in carbon fiber-reinforced concrete, monitored by electrical resistance measurement. Cem. Concr. Res. 2000, 30, 651–659. [Google Scholar] [CrossRef]
- Chen, B.; Wu, K.; Yao, W. Conductivity of carbon fiber reinforced cement-based composites. Cem. Concr. Compos. 2004, 26, 291–297. [Google Scholar] [CrossRef]
- Wang, W.; Dai, H.Z.; Wu, S.G. Mechanical behavior and electrical property of CFRC-strengthened RC beams under fatigue and monotonic loading. Mater. Sci. Eng. A 2008, 479, 191–196. [Google Scholar] [CrossRef]
- Chung, D.D.L. Carbon materials for structural self-sensing, electromagnetic shielding and thermal interfacing. Carbon 2012, 50, 3342–3353. [Google Scholar] [CrossRef]
- Azhari, F.; Banthia, N. Cement-based sensors with carbon fibers and carbon nanotubes for piezoresistive sensing. Cem. Concr. Compos. 2012, 34, 866–873. [Google Scholar] [CrossRef]
- Han, B.G.; Zhang, L.Q.; Sun, S.W.; Yu, X.; Dong, X.F.; Wu, T.J.; Ou, J.P. Electrostatic self-assembled carbon nanotube/nano carbon black composite fillers reinforced cement-based materials with multifunctionality. Compos. Part A 2015, 79, 103–115. [Google Scholar] [CrossRef]
- Song, J.D.; Nguyen, D.L.; Manathamsombat, C.; Kim, D.J. Effect of fiber volume content on electromechanical behavior of strain-hardening steel-fiber-reinforced cementitious composites. Compos. Mater. 2015, 49, 3621–3634. [Google Scholar] [CrossRef]
- Nguyen, D.L.; Song, J.D.; Manathamsombat, C.; Kim, D.J. Comparative electromechanical damage-sensing behaviors of six strain-hardening steel fiber-reinforced cementitious composites under direct tension. Compos. Part B 2015, 69, 159–168. [Google Scholar] [CrossRef]
- Kim, M.K.; Kim, D.J.; An, Y.K. Electro-mechanical self-sensing response of ultra-high-performance fiber-reinforced concrete in tension. Compos. Part B 2018, 134, 254–264. [Google Scholar] [CrossRef]
- Materazzi, A.L.; Ubertini, F.; D’Alessandro, A. Carbon nanotube cement-based transducers for dynamic sensing of strain. Cem. Concr. Compos. 2013, 37, 2–11. [Google Scholar] [CrossRef]
- Pisello, A.L.; D’Alessandro, A.; Sambuco, S.; Rallini, M.; Ubertini, F.; Asdrubali, F.; Materizzi, A.L.; Cotana, F. Multipurpose experimental characterization of smart nanocomposite cement-based materials for thermal-energy efficiency and strain-sensing capability. Sol. Energy Mater. Sol. Cells 2017, 161, 77–88. [Google Scholar] [CrossRef]
- Hou, T.C.; Lynch, J.P. Electrical impedance tomographic methods for sensing strain fields and crack damage in cementitious structures. J. Intell. Mater. Syst. Struct. 2008, 20, 1363–1379. [Google Scholar] [CrossRef]
- Hallaji, M.; Seppanen, A.; Pour-Ghaz, M. Electrical impedance tomography-based sensing skin for quantitative imaging of damage in concrete. Smart. Mater. Struct. 2014, 23, 085001. [Google Scholar] [CrossRef]
- Gupta, S.; Gonzalez, J.G.; Loh, K.J. Self-sensing concrete enabled by nano-engineered interfaces. Struct. Health. Monit. 2016, 16, 309–323. [Google Scholar] [CrossRef]
- Konsta-Gdoutos, M.S.; Aza, C.A. Self sensing carbon nanotube (CNT) and nanofiber (CNF) cementitious composites for real time damage assessment in smart structures. Cem. Concr. Compos. 2014, 53, 162–169. [Google Scholar] [CrossRef]
- Han, B.H.; Guan, X.C.; Ou, J.P. Electrode design, measuring method and data acquisition system of carbon fiber cement paste piezoresistive sensors. Sens. Actuators A 2007, 135, 360–369. [Google Scholar] [CrossRef]
- Azhari, F. Cement-based sensors for structural health monitoring. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2008. [Google Scholar]
- Hou, T.C.; Lynch, J.P. Conductivity-based strain monitoring and damage characterization of fiber reinforced cementitious structural components. In Smart Structures and Materials 2005: Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems; International Society of Optics and Photonics: Bellingham, UK, 2005; pp. 419–430. [Google Scholar]
- Ding, Y.N.; Han, Z.B.; Zhang, Y.L.; Aguiar, J.B. Concrete with triphasic conductive materials for self-monitoring of cracking development subjected to flexure. Compos. Struct. 2016, 138, 184–191. [Google Scholar] [CrossRef]
- Han, B.G.; Zhang, L.Q.; Zhang, C.Y.; Wang, Y.Y.; Yu, X.; Ou, J.P. Reinforcement effect and mechanism of carbon fibers to mechanical and electrically conductive properties of cement-based materials. Constr. Build. Mater. 2016, 125, 479–489. [Google Scholar] [CrossRef]
- Le, H.V.; Kim, D.J. Effect of matrix cracking on electrical resistivity of high performance fiber reinforced cementitious composites in tension. Constr. Build. Mater. 2017, 156, 750–760. [Google Scholar] [CrossRef]
- Han, B.G.; Ou, J.P. Embedded piezoresistive cement-based stress/strain sensor. Sens. Actuators A 2007, 138, 294–298. [Google Scholar] [CrossRef]
- Sun, S.W.; Han, B.G.; Shan, J.; Yu, X.; Wang, Y.L.; Li, H.Y.; Ou, J.P. Nano graphite platelets-enabled piezoresistive cementitious composites for structural health monitoring. Constr. Build. Mater. 2017, 136, 314–328. [Google Scholar] [CrossRef]
- Wenner, F. A method for measuring earth resistivity. J. Washington Acad. Sci. 1915, 5, 561–563. [Google Scholar] [CrossRef]
- Kim, M.K.; Kim, D.J. Electromechanical response of high-performance fiber-reinforced cementitious composites containing milled glass fibers under tension. Materials 2018, 11, 1115. [Google Scholar] [CrossRef] [PubMed]
- Downey, A.; D’Alessandro, A.; Ubertini, F.; Laflamme, S.; Geiger, R. Biphasic DC measurement approach for enhanced measurement stability and multi-channel sampling of self-sensing multi-functional structural materials doped with carbon-based additives. Smart. Mater. Struct. 2017, 26, 065008. [Google Scholar] [CrossRef]
- Suryanto, B.; McCarter, W.J.; Starrs, G.; Ludford-Jones, G.V. Electrochemical immittance spectroscopy applied to a hybrid PVA/steel fiber engineered cementitious composite. Mater. Design. 2016, 105, 179–189. [Google Scholar] [CrossRef]
- Alexander, C.K.; Sadiku, M.N.O. Basic Concepts. In Fundamentals of Electric Circuits; McGraw-Hill Education: Columbus, OH, USA, 2013. [Google Scholar]












| Electrode Material | Thickness, t (mm) | Width, w (mm) | Length, l (mm) | Cross-Section, A (mm2) † | Electrical Resistivity (× 10−7 kΩ·cm) |
|---|---|---|---|---|---|
| Copper tape | 0.12 | 10 | 100 | 1.20 | 0.058 a |
| Copper film | 0.30 | 5 | 50 | 1.50 | 0.023 b |
| Carbon tape type 1 | 0.16 | 10 | 100 | 1.60 | 1.3 a |
| Carbon tape type 2 | 0.18 | 5 | 100 | 0.90 | 1.3 a |
| Copper wire | 0.16 * | 1000 | 0.02 | 0.000017 a | |
| Cement (Type III) | Silica Sand (#40) * | Fly Ash | Super-Plasticizer ** | Water | Compressive Strength (MPa) |
|---|---|---|---|---|---|
| 1.0 | 1.0 | 0.15 | 0.0055 | 0.35 | 95 |
| Fiber Type | Diameter (mm) | Length (mm) | Density (g/cc) | Tensile Strength (MPa) | Elastic Modulus (GPa) | Electrical Resistivity (× 10−10 kΩ·cm) * |
|---|---|---|---|---|---|---|
| Long smooth | 0.3 | 30 | 7.90 | 2447 | 200 | 6.9 |
| Medium smooth | 0.2 | 19.5 | 7.90 | 2942 | 200 | 5.4 |
| Type of Electrode | No. | Electrical Resistivity (kΩ·cm) | Fractional Change in Electrical Resistivity (%) | Slope at Polarization Time (kΩ·cm/s) * | Polarization Time (s) | ||
|---|---|---|---|---|---|---|---|
| ρ0 | ρP | ∆ρP | d∆ρP/dtp | tp | |||
| CS | SP1 | 2.2 | 4.0 | 0.10 | 190.8 | 0.0020 | 30 |
| SP2 | 3.2 | 5.5 | 0.12 | 173.8 | 0.0020 | 30 | |
| SP3 | 2.7 | 5.3 | 0.06 | 195.5 | 0.0040 | 20 | |
| Avg. a | 2.7 | 4.9 | 0.09 | 186.7 | 0.0027 | 25 | |
| STD b | 0.4 | 0.7 | 0.02 | 9.3 | 0.0009 | 4.7 | |
| CC1 | SP1 | 2.8 | 8.1 | 0.13 | 295.8 | 0.0010 | 110 |
| SP2 | 3.8 | 8.1 | 0.08 | 211.3 | 0.0000 | 90 | |
| SP3 | 2.8 | 6.4 | 0.04 | 214.9 | 0.0000 | 40 | |
| Avg. | 3.2 | 7.5 | 0.08 | 240.7 | 0.0000 | 80 | |
| STD | 0.5 | 0.8 | 0.04 | 39.0 | 0.0005 | 29.4 | |
| CC2 | SP1 | 14.6 | 26.5 | 0.07 | 180.3 | 0.0010 | 100 |
| SP2 | 16.5 | 34.6 | 0.11 | 210.6 | 0.0010 | 130 | |
| SP3 | 15.5 | 27.7 | 0.04 | 180.5 | 0.0060 | 90 | |
| Avg. | 15.5 | 29.6 | 0.07 | 190.5 | 0.0027 | 107 | |
| STD | 0.8 | 3.6 | 0.03 | 14.2 | 0.0024 | 17.0 | |
| WC2 | SP1 | 51.0 | - | ||||
| SP2 | 48.8 | ||||||
| SP3 | 71.3 | ||||||
| Avg. | 57.0 | ||||||
| STD | 10.1 | ||||||
| Notation | Tensile Strain (%) | Tensile Stress (MPa) | Electrical Resistivity (kΩ-cm) | Change in the Electrical Resistivity (kΩ-cm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| εcc | εpc | σcc | σpc | ρ0 | ρcc | ρpc | ∆ρ | ∆ρ1 | ∆ρ2 | ||
| CS | SP1 | 0.01 | 0.44 | 6.0 | 13.3 | 5.1 | 4.3 | 4.2 | 0.9 | 0.8 | 0.1 |
| SP2 | 0.02 | 0.48 | 6.0 | 15.8 | 7.1 | 6.9 | 2.2 | 4.9 | 0.2 | 4.7 | |
| SP3 | 0.02 | 0.51 | 4.5 | 15.4 | 10.4 | 10.2 | 4.9 | 5.6 | 0.3 | 5.3 | |
| Avg. | 0.02 | 0.48 | 5.5 | 14.9 | 8.8 | 8.5 | 3.5 | 5.3 | 0.3 | 5.0 | |
| STD | 0.00 | 0.02 | 0.75 | 0.20 | 1.65 | 1.65 | 1.35 | 0.35 | 0.05 | 0.30 | |
| CC1 | SP1 | 0.03 | 0.50 | 5.3 | 15.1 | 12.8 | 12.7 | 8.5 | 5.2 | 1.0 | 4.2 |
| SP2 | 0.02 | 0.54 | 6.4 | 15.5 | 12.1 | 11.4 | 7.3 | 4.8 | 0.6 | 4.2 | |
| SP3 | 0.03 | 0.65 | 7.4 | 15.7 | 17.4 | 16.4 | 11.9 | 5.6 | 1.1 | 5.6 | |
| Avg. | 0.03 | 0.56 | 6.4 | 15.4 | 14.1 | 13.5 | 9.2 | 4.9 | 0.6 | 4.3 | |
| STD | 0.00 | 0.06 | 0.86 | 0.25 | 2.35 | 2.12 | 1.95 | 0.33 | 0.22 | 0.66 | |
| Notation | Overall Sensing Capacity, GF | Strain-Sensing Capacity, GF1 | Damage-Sensing Capacity, GF2 | |
|---|---|---|---|---|
| CS | SP1 ¥ | 0.40 | 15.69 | 0.05 |
| SP2 | 1.44 | 1.41 | 1.48 | |
| SP3 | 1.06 | 1.44 | 1.06 | |
| Avg. | 1.22 | 1.43 | 1.23 | |
| STD | 0.19 | 0.02 | 0.21 | |
| CC1 | SP1 | 0.81 | 2.60 | 0.70 |
| SP2 | 0.73 | 2.48 | 0.71 | |
| SP3 | 0.50 | 2.11 | 0.56 | |
| Avg. | 0.62 | 2.39 | 0.65 | |
| STD | 0.13 | 0.21 | 0.07 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, H.W.; Kim, M.K.; Kim, D.J. Comparative Performance of Four Electrodes for Measuring the Electromechanical Response of Self-Damage Detecting Concrete under Tensile Load. Sensors 2019, 19, 3645. https://doi.org/10.3390/s19173645
Noh HW, Kim MK, Kim DJ. Comparative Performance of Four Electrodes for Measuring the Electromechanical Response of Self-Damage Detecting Concrete under Tensile Load. Sensors. 2019; 19(17):3645. https://doi.org/10.3390/s19173645
Chicago/Turabian StyleNoh, Hyeon Woo, Min Kyoung Kim, and Dong Joo Kim. 2019. "Comparative Performance of Four Electrodes for Measuring the Electromechanical Response of Self-Damage Detecting Concrete under Tensile Load" Sensors 19, no. 17: 3645. https://doi.org/10.3390/s19173645
APA StyleNoh, H. W., Kim, M. K., & Kim, D. J. (2019). Comparative Performance of Four Electrodes for Measuring the Electromechanical Response of Self-Damage Detecting Concrete under Tensile Load. Sensors, 19(17), 3645. https://doi.org/10.3390/s19173645





