Wavelet-Based Analysis of Physical Activity and Sleep Movement Data from Wearable Sensors among Obese Adults
Abstract
:1. Introduction
2. Materials and Methods
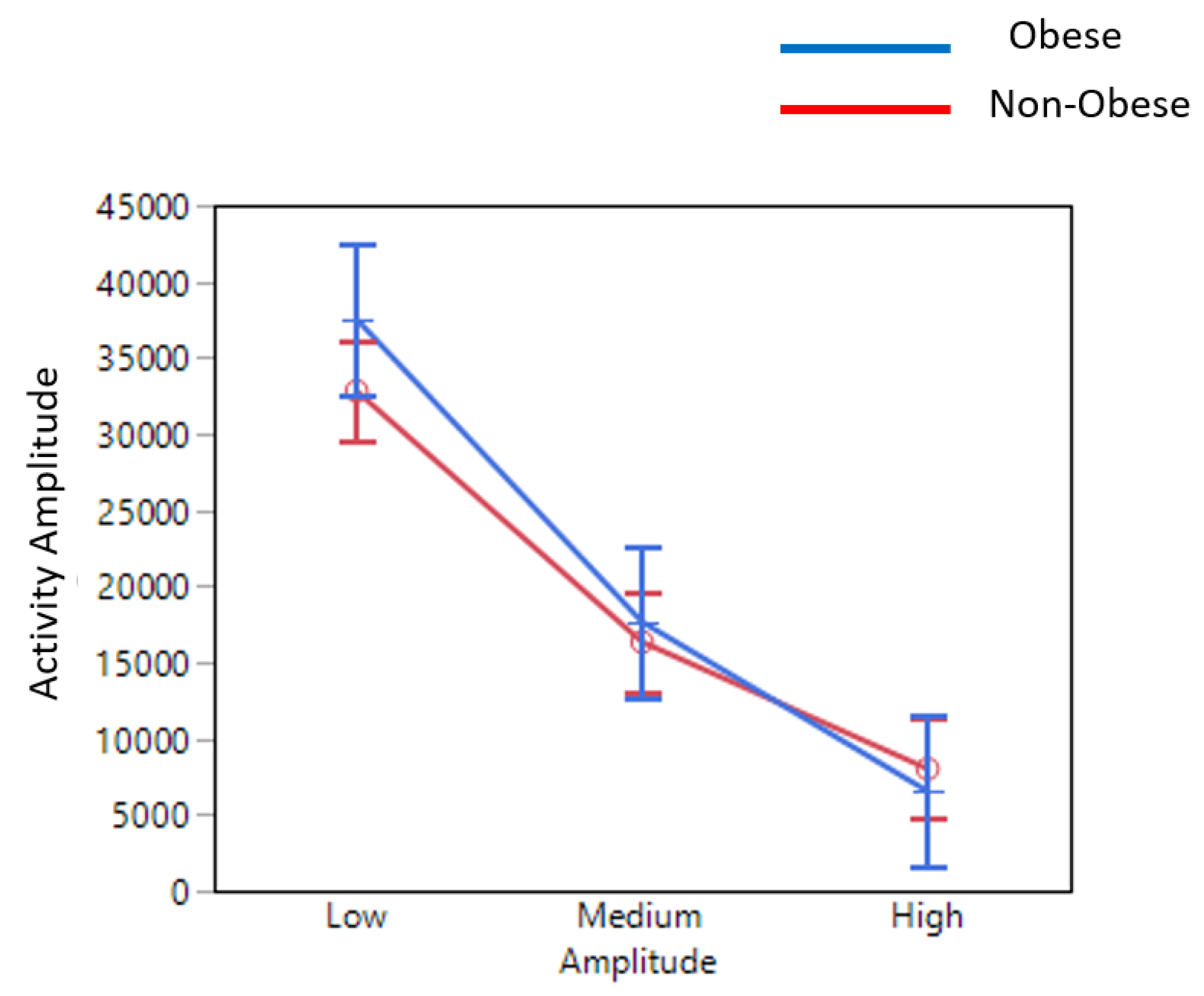
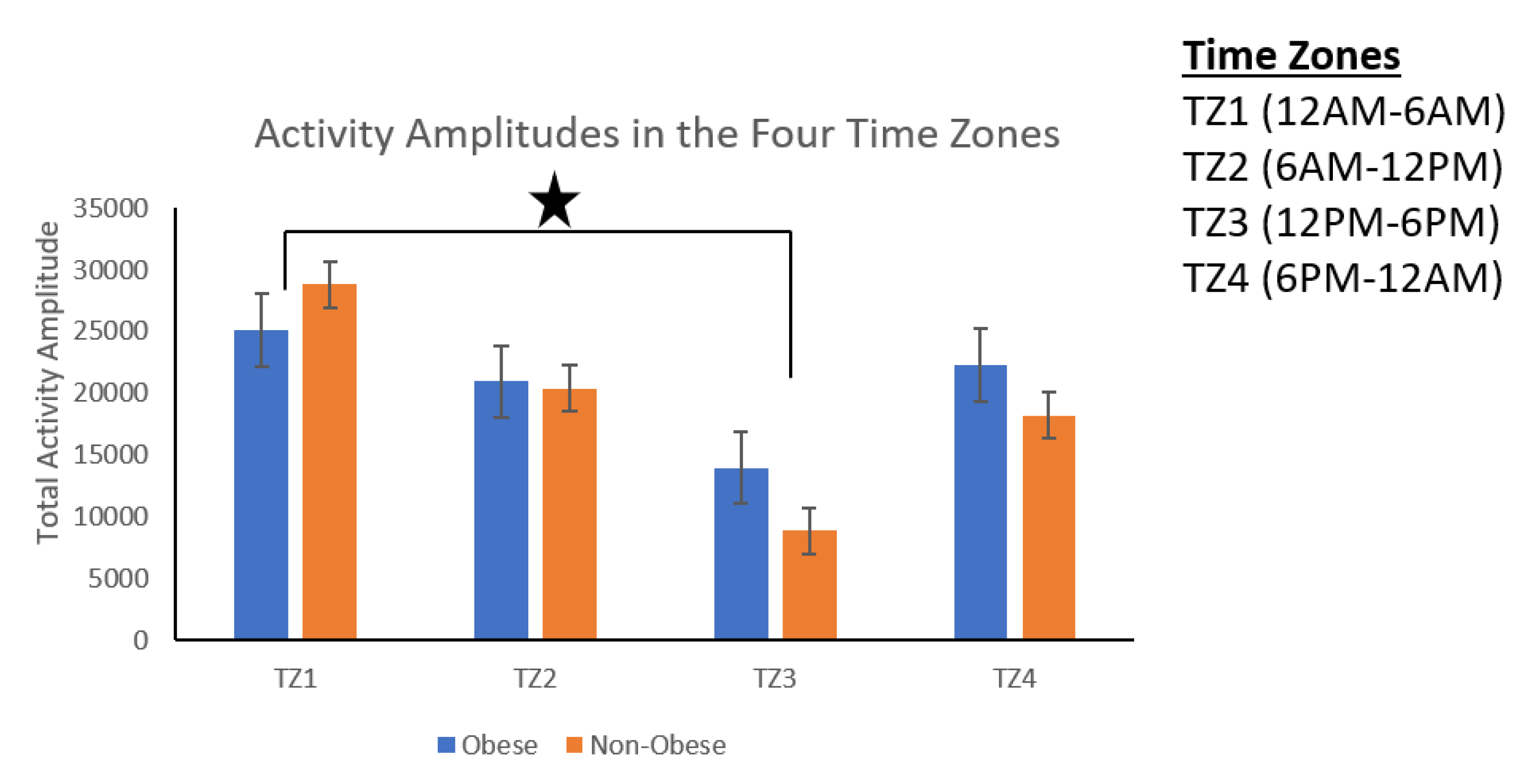
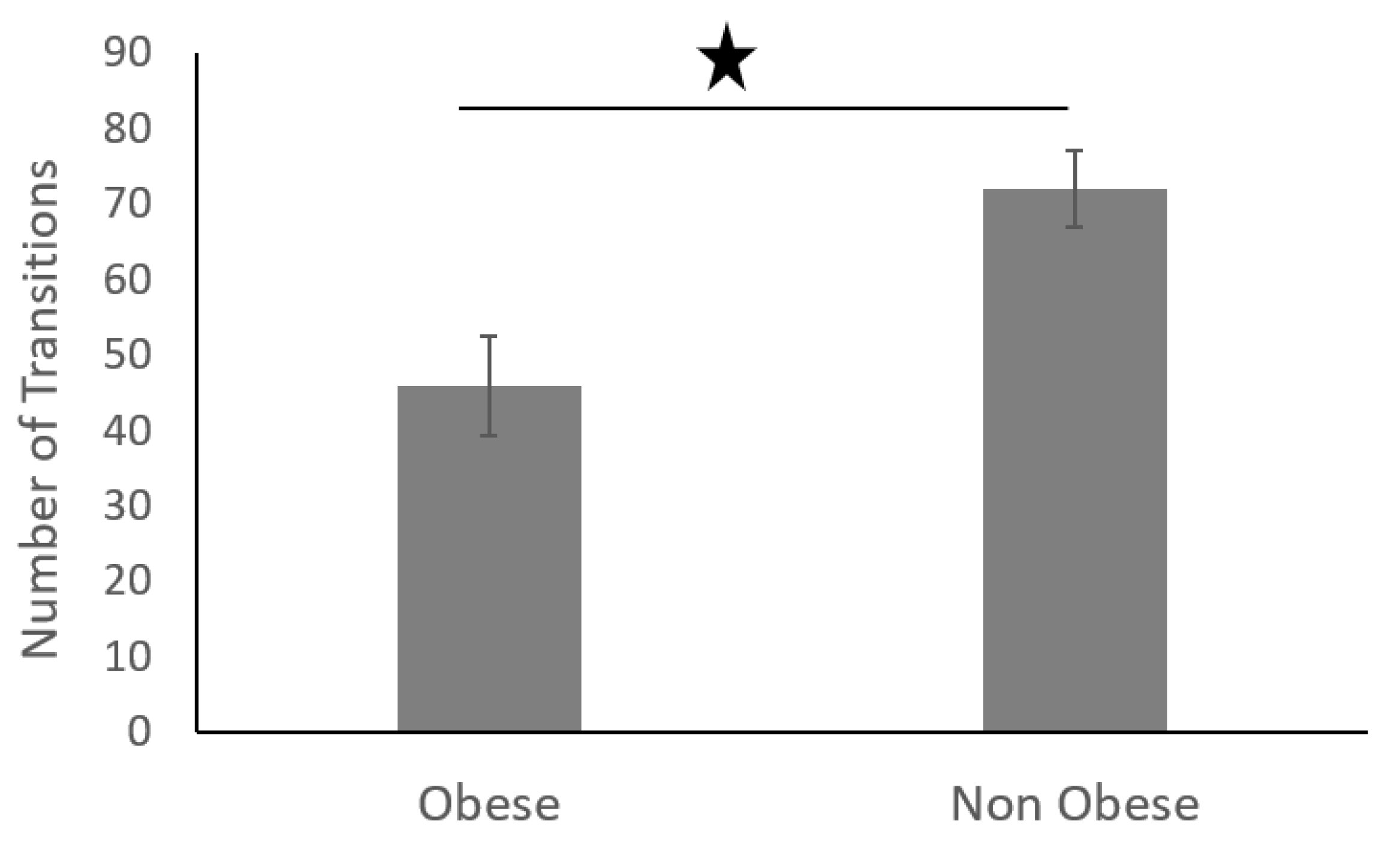
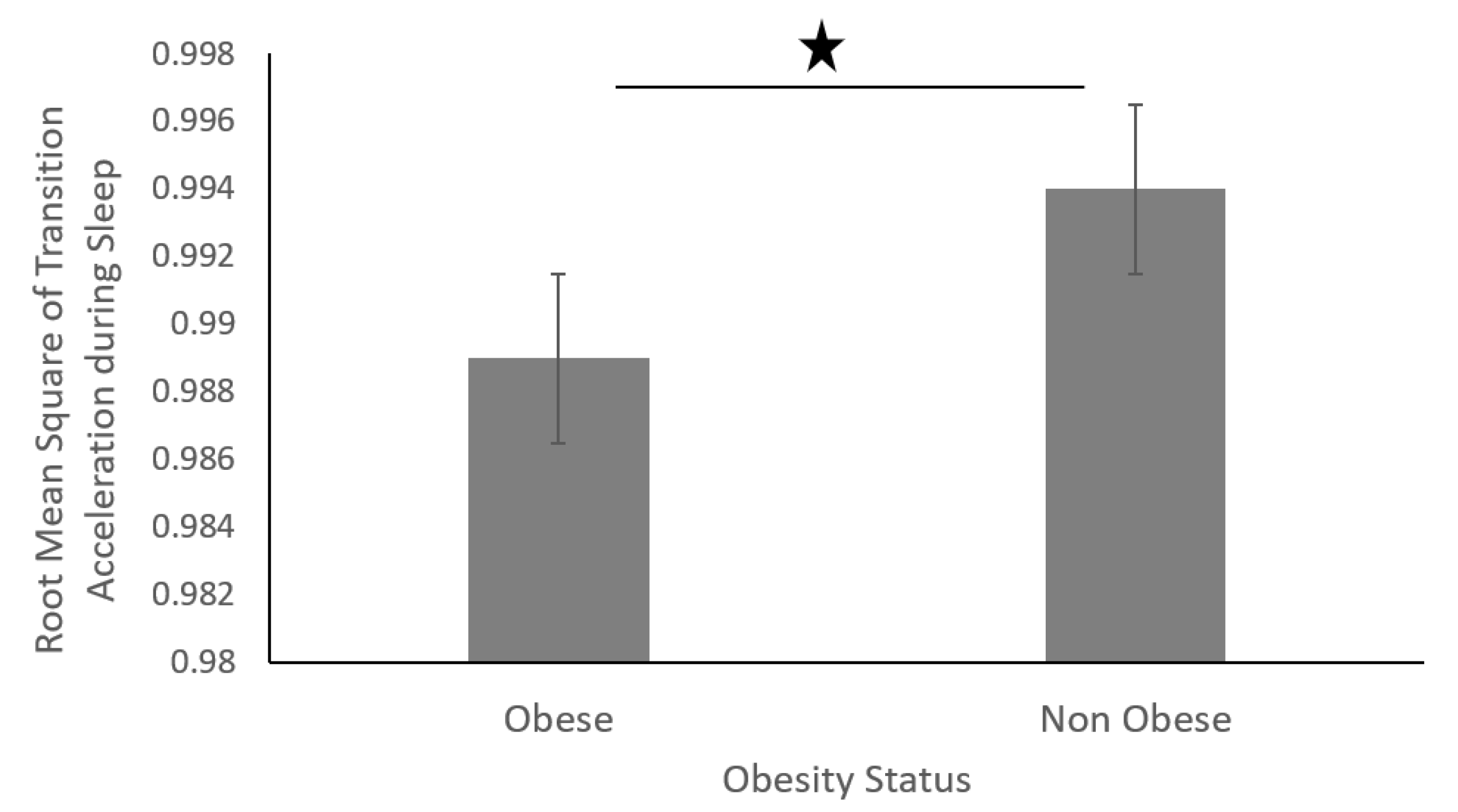
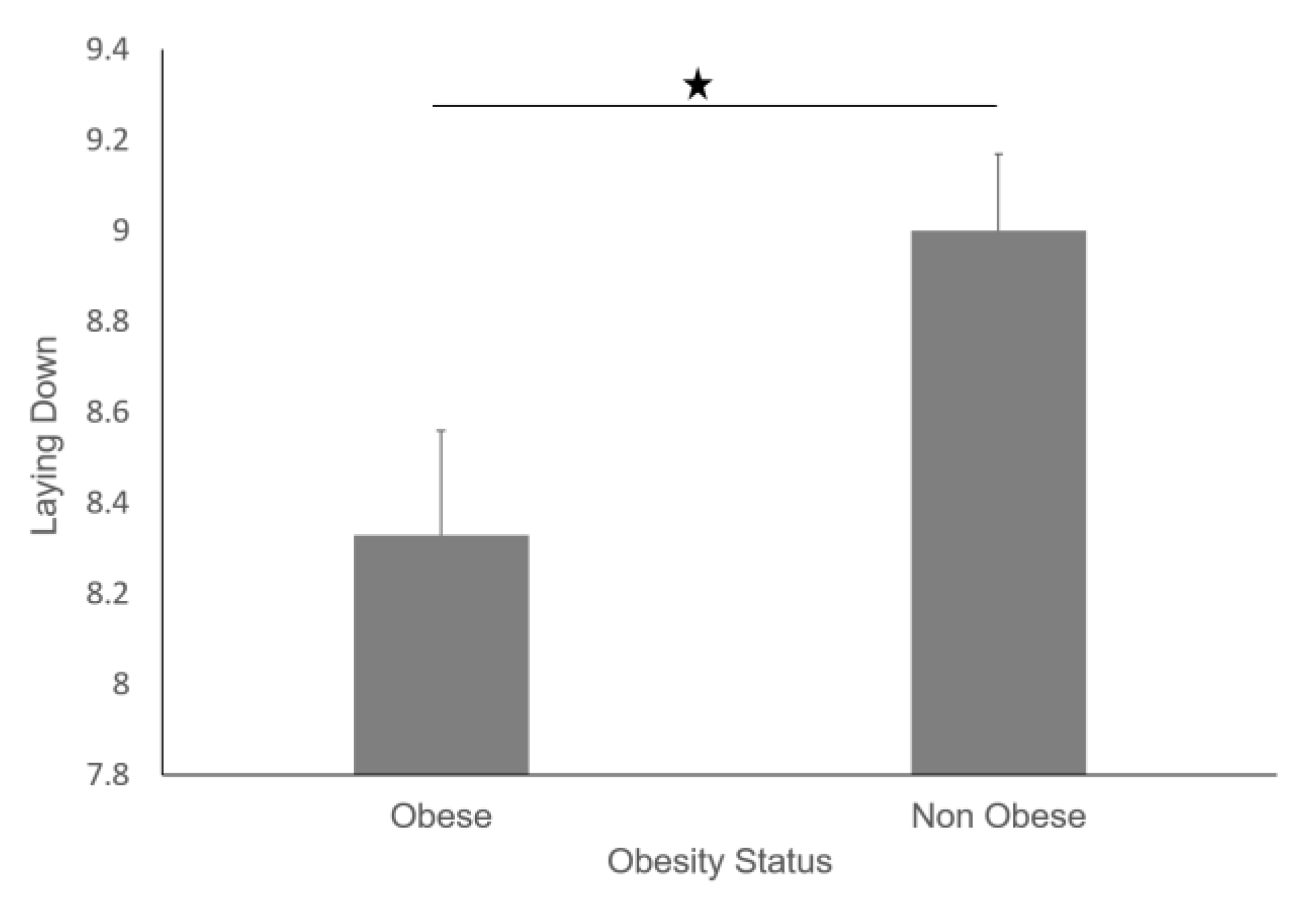
3. Results
4. Discussion
5. Limitations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, L.; Colditz, G.A. Prevalence of Overweight and Obesity in the United States, 2007–2012. JAMA Intern. Med. 2015, 175, 1412–1413. [Google Scholar] [CrossRef] [PubMed]
- Finkelstein, E.A.; Trogdon, J.G.; Cohen, J.W.; Dietz, W. Annual medical spending attributable to obesity: Payer-and service-specific estimates. Health Aff. 2009, 28, w822–w831. [Google Scholar] [CrossRef] [PubMed]
- Finkelstein, E.A.; Khavjou, O.A.; Thompson, H.; Trogdon, J.G.; Pan, L.; Sherry, B.; Dietz, W. Obesity and severe obesity forecasts through 2030. Am. J. Prev. Med. 2012, 42, 563–570. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.C.; McPherson, K.; Marsh, T.; Gortmaker, S.L.; Brown, M. Health and economic burden of the projected obesity trends in the USA and the UK. Lancet 2011, 378, 815–825. [Google Scholar] [CrossRef]
- World Health Organization. Global Health Observatory (GHO) Data 2018; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Klein, S.; Burke, L.E.; Bray, G.A.; Blair, S.; Allison, D.B.; Pi-Sunyer, X.; Hong, Y.; Eckel, R.H.; American Heart Association Council on Nutrition, Physical Activity, and Metabolism. Clinical implications of obesity with specific focus on cardiovascular disease: A statement for professionals from the American Heart Association Council on Nutrition, Physical Activity, and Metabolism: Endorsed by the American College of Cardiology Foundation. Circulation 2004, 110, 2952–2967. [Google Scholar]
- Global Burden of Metabolic Risk Factors for Chronic Diseases Collaboration; Lu, Y.; Hajifathalian, K.; Ezzati, M.; Woodward, M.; Rimm, E.B.; Danaei, G. Metabolic mediators of the effects of body-mass index, overweight, and obesity on coronary heart disease and stroke: A pooled analysis of 97 prospective cohorts with 1.8 million participants. Lancet 2014, 383, 970–983. [Google Scholar]
- McGee, D.L.; Diverse Populations Collaboration. Body mass index and mortality: A meta-analysis based on person-level data from twenty-six observational studies. Ann. Epidemiol. 2005, 15, 87–97. [Google Scholar] [CrossRef]
- Must, A.; Spadano, J.; Coakley, E.H.; Field, A.E.; Colditz, G.; Dietz, W.H. The disease burden associated with overweight and obesity. JAMA 1999, 282, 1523–1529. [Google Scholar] [CrossRef]
- NCD Risk Factor Collaboration. Worldwide trends in body-mass index, underweight, overweight, and obesity from 1975 to 2016: A pooled analysis of 2416 population-based measurement studies in 128.9 million children, adolescents, and adults. Lancet 2017, 390, 2627–2642. [Google Scholar] [CrossRef]
- Adams, K.F.; Schatzkin, A.; Harris, T.B.; Kipnis, V.; Mouw, T.; Ballard-Barbash, R.; Hollenbeck, A.; Leitzmann, M.F. Overweight, Obesity, and Mortality in a Large Prospective Cohort of Persons 50 to 71 Years Old. N. Engl. J. Med. 2006, 355, 763–778. [Google Scholar] [CrossRef]
- Sarma, S.; Zaric, G.S.; Campbell, M.K.; Gilliland, J. The effect of physical activity on adult obesity: Evidence from the Canadian NPHS panel. Econ. Hum. Biol. 2014, 14, 1–21. [Google Scholar] [CrossRef]
- Haskell, W.L.; Lee, I.M.; Pate, R.R.; Powell, K.E.; Blair, S.N.; Franklin, B.A.; Macera, C.A.; Heath, G.W.; Thompson, P.D.; Bauman, A. Physical activity and public health: Updated recommendation for adults from the American College of Sports Medicine and the American Heart Association. Med. Sci. Sports Exerc. 2007, 39, 1423–1434. [Google Scholar] [CrossRef]
- Flegal, K.M.; Carroll, M.D.; Kuczmarski, R.J.; Johnson, C.L. Overweight and obesity in the United States: Prevalence and trends, 1960–1994. Int. J. Obes. Relat. Metab. Disord. 1998, 22, 39–47. [Google Scholar] [CrossRef]
- Hedley, A.A.; Ogden, C.L.; Johnson, C.L.; Carroll, M.D.; Curtin, L.R.; Flegal, K.M. Prevalence of overweight and obesity among US children, adolescents, and adults, 1999–2002. JAMA 2004, 291, 2847–2850. [Google Scholar] [CrossRef]
- Kuczmarski, R.J.; Flegal, K.M.; Campbell, S.M.; Johnson, C.L. Increasing prevalence of overweight among US adults. The National Health and Nutrition Examination Surveys, 1960 to 1991. JAMA 1994, 272, 205–211. [Google Scholar] [CrossRef]
- Laskowski, E.R. The role of exercise in the treatment of obesity. PM R 2012, 4, 840–844. [Google Scholar] [CrossRef]
- Tudor-Locke, C.; Bassett, D.R. How Many Steps/Day Are Enough? Sports Med. 2004, 34, 1–8. [Google Scholar] [CrossRef]
- Buman, M.P.; Hekler, E.B.; Haskell, W.L.; Pruitt, L.; Conway, T.L.; Cain, K.L.; Sallis, J.F.; Saelens, B.E.; Frank, L.D.; King, A.C. Objective light-intensity physical activity associations with rated health in older adults. Am. J. Epidemiol. 2010, 172, 1155–1165. [Google Scholar] [CrossRef]
- Healy, G.N.; Dunstan, D.W.; Salmon, J.; Cerin, E.; Shaw, J.E.; Zimmet, P.Z.; Owen, N. Objectively measured light-intensity physical activity is independently associated with 2-h plasma glucose. Diabetes Care 2007, 30, 1384–1389. [Google Scholar] [CrossRef]
- Healy, G.N.; Matthews, C.E.; Dunstan, D.W.; Winkler, E.A.; Owen, N. Sedentary time and cardio-metabolic biomarkers in US adults: NHANES 2003–06. Eur. Heart J. 2011, 32, 590–597. [Google Scholar] [CrossRef]
- Thorp, A.A.; Owen, N.; Neuhaus, M.; Dunstan, D.W. Sedentary behaviors and subsequent health outcomes in adults a systematic review of longitudinal studies, 1996–2011. Am. J. Prev. Med. 2011, 41, 207–215. [Google Scholar] [CrossRef]
- Katzmarzyk, P.T.; Church, T.S.; Craig, C.L.; Bouchard, C. Sitting time and mortality from all causes, cardiovascular disease, and cancer. Med. Sci. Sports Exerc. 2009, 41, 998–1005. [Google Scholar] [CrossRef]
- Patel, S.R.; Hu, F.B. Short sleep duration and weight gain: A systematic review. Obesity 2008, 16, 643–653. [Google Scholar] [CrossRef]
- Cappuccio, F.P.; Cooper, D.; D’Elia, L.; Strazzullo, P.; Miller, M.A. Sleep duration predicts cardiovascular outcomes: A systematic review and meta-analysis of prospective studies. Eur. Heart J. 2011, 32, 1484–1492. [Google Scholar] [CrossRef]
- Gangwisch, J.E.; Heymsfield, S.B.; Boden-Albala, B.; Buijs, R.M.; Kreier, F.; Pickering, T.G.; Rundle, A.G.; Zammit, G.K.; Malaspina, D. Sleep duration as a risk factor for diabetes incidence in a large U.S. sample. Sleep 2007, 30, 1667–1673. [Google Scholar] [CrossRef]
- Patel, S.R. Reduced sleep as an obesity risk factor. Obes. Rev. 2009, 10 (Suppl. 2), 61–68. [Google Scholar] [CrossRef]
- Bassett, D.R., Jr.; Rowlands, A.; Trost, S.G. Calibration and validation of wearable monitors. Med. Sci. Sports Exerc. 2012, 44 (Suppl. 1), S32–S38. [Google Scholar] [CrossRef]
- Sadeh, A. The role and validity of actigraphy in sleep medicine: An update. Sleep Med. Rev. 2011, 15, 259–267. [Google Scholar] [CrossRef]
- Miwa, H.; Sasahara, S.; Matsui, T. Roll-over Detection and Sleep Quality Measurement using a Wearable Sensor. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2007, 2007, 1507–1510. [Google Scholar]
- Lee, J.M.; Byun, W.; Keill, A.; Dinkel, D.; Seo, Y. Comparison of Wearable Trackers‘ Ability to Estimate Sleep. Int. J. Environ. Res. Public Health 2018, 15, 1265. [Google Scholar] [CrossRef]
- Peake, J.M.; Kerr, G.; Sullivan, J.P. A Critical Review of Consumer Wearables, Mobile Applications, and Equipment for Providing Biofeedback, Monitoring Stress, and Sleep in Physically Active Populations. Front. Physiol. 2018, 9, 743. [Google Scholar] [CrossRef]
- Jalloul, N. Wearable sensors for the monitoring of movement disorders. Biomed. J. 2018, 41, 249–253. [Google Scholar] [CrossRef]
- Cooper, C.; Gross, A.; Brinkman, C.; Pope, R.; Allen, K.; Hastings, S.; Bogen, B.E.; Goode, A.P. The impact of wearable motion sensing technology on physical activity in older adults. Exp. Gerontol. 2018, 112, 9–19. [Google Scholar] [CrossRef]
- Buman, M.P.; King, A.C. Exercise as a Treatment to Enhance Sleep. Am. J. Lifestyle Med. 2010, 4, 500–514. [Google Scholar] [CrossRef]
- Lockhart, T.E.; Soangra, R.; Zhang, J.; Wu, X. Wavelet based automated postural event detection and activity classification with single imu-biomed 2013. Biomed. Sci. Instrum. 2013, 49, 224–233. [Google Scholar]
- Soangra, R.; Lockhart, T.E. A comparative study for performance evaluation of sit-to-stand task with body worn sensor and existing laboratory methods. Biomed. Sci. Instrum. 2012, 48, 407–414. [Google Scholar]
- Thompson, D.; Edelsberg, J.; Kinsey, K.L.; Oster, G. Estimated economic costs of obesity to U.S. business. Am. J. Health Promot. 1998, 13, 120–127. [Google Scholar] [CrossRef]
- Tomlinson, D.J.; Erskine, R.M.; Morse, C.I.; Winwood, K.; Onambélé-Pearson, G. The impact of obesity on skeletal muscle strength and structure through adolescence to old age. Biogerontology 2016, 17, 467–483. [Google Scholar] [CrossRef]
- Gadducci, A.V.; de Cleva, R.; Santarém, G.C.D.; Silva, P.R.S.; Greve, J.M.D.; Santo, M.A. Muscle strength and body composition in severe obesity. Clinics 2017, 72, 272–275. [Google Scholar] [CrossRef]
- Chomistek, A.K.; Shiroma, E.J.; Lee, I.M. The Relationship Between Time of Day of Physical Activity and Obesity in Older Women. J. Phys. Act. Health 2016, 13, 416–418. [Google Scholar] [CrossRef]
- Teasdale, N.; Simoneau, M.; Corbeil, P.; Handrigan, G.; Tremblay, A.; Hue, O. Obesity Alters Balance and Movement Control. Curr. Obes. Rep. 2013, 2, 235–240. [Google Scholar] [CrossRef] [Green Version]
- Beccuti, G.; Pannain, S. Sleep and obesity. Curr. Opin. Clin. Nutr. Metab. Care 2011, 14, 402–412. [Google Scholar] [CrossRef] [Green Version]
- Cooper, C.B.; Neufeld, E.V.; Dolezal, B.A.; Martin, J.L. Sleep deprivation and obesity in adults: A brief narrative review. BMJ Open Sport Exerc. Med. 2018, 4, e000392. [Google Scholar] [CrossRef]
- Pietilainen, K.H.; Kaprio, J.; Borg, P.; Plasqui, G.; Yki-Järvinen, H.; Kujala, U.M.; Rose, R.J.; Westerterp, K.R.; Rissanen, A. Physical inactivity and obesity: A vicious circle. Obesity 2008, 16, 409–414. [Google Scholar] [CrossRef]


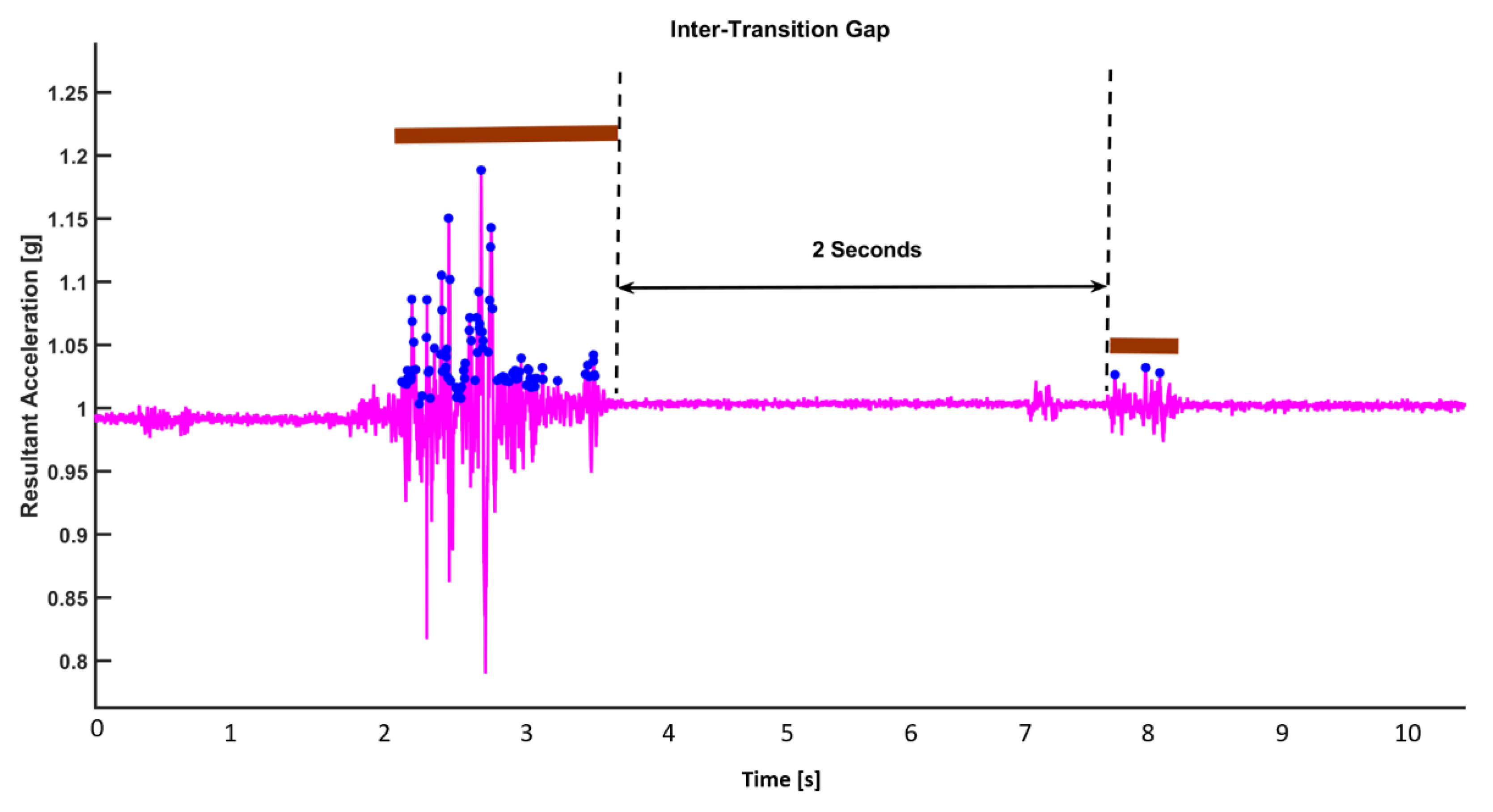
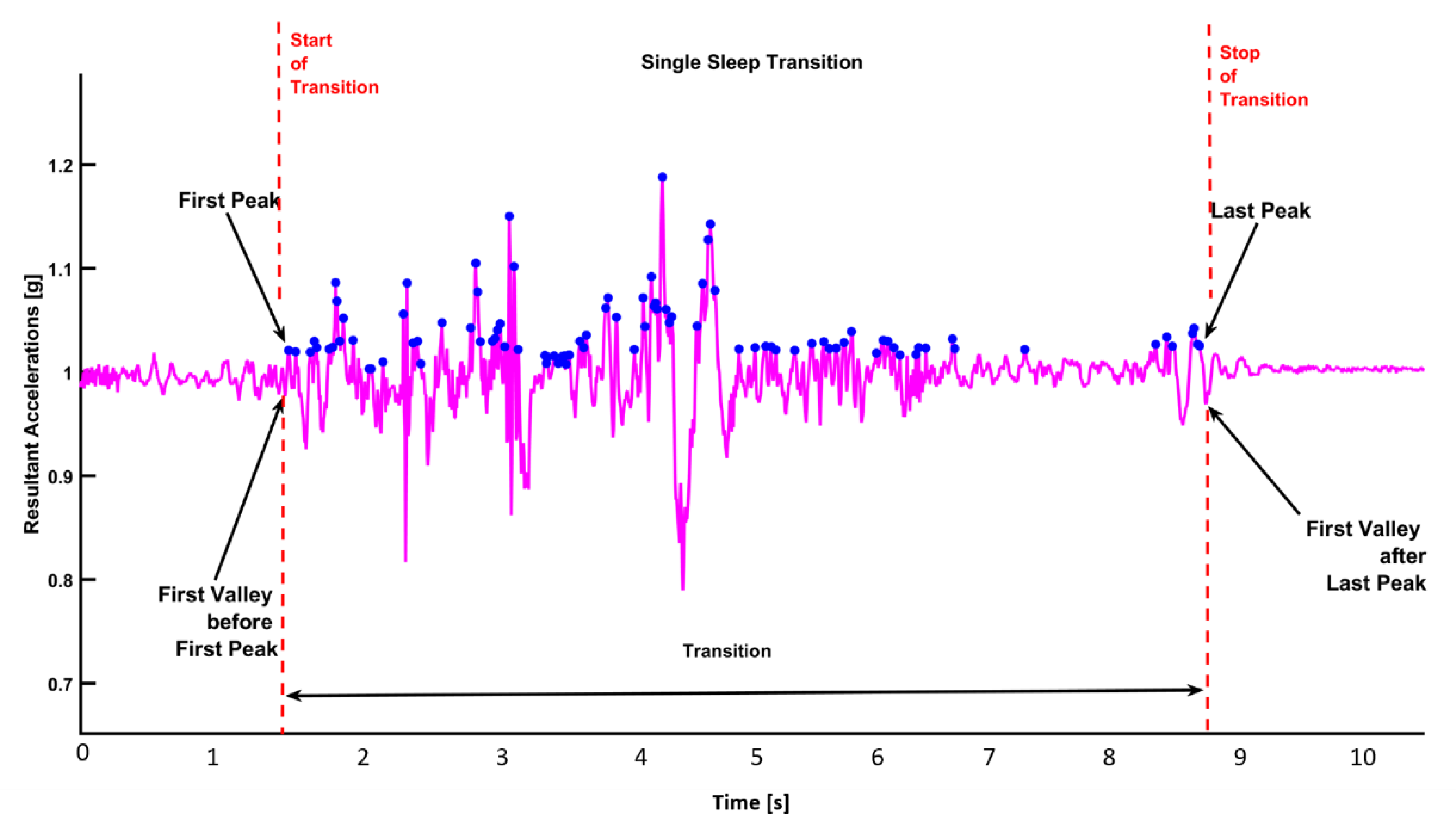



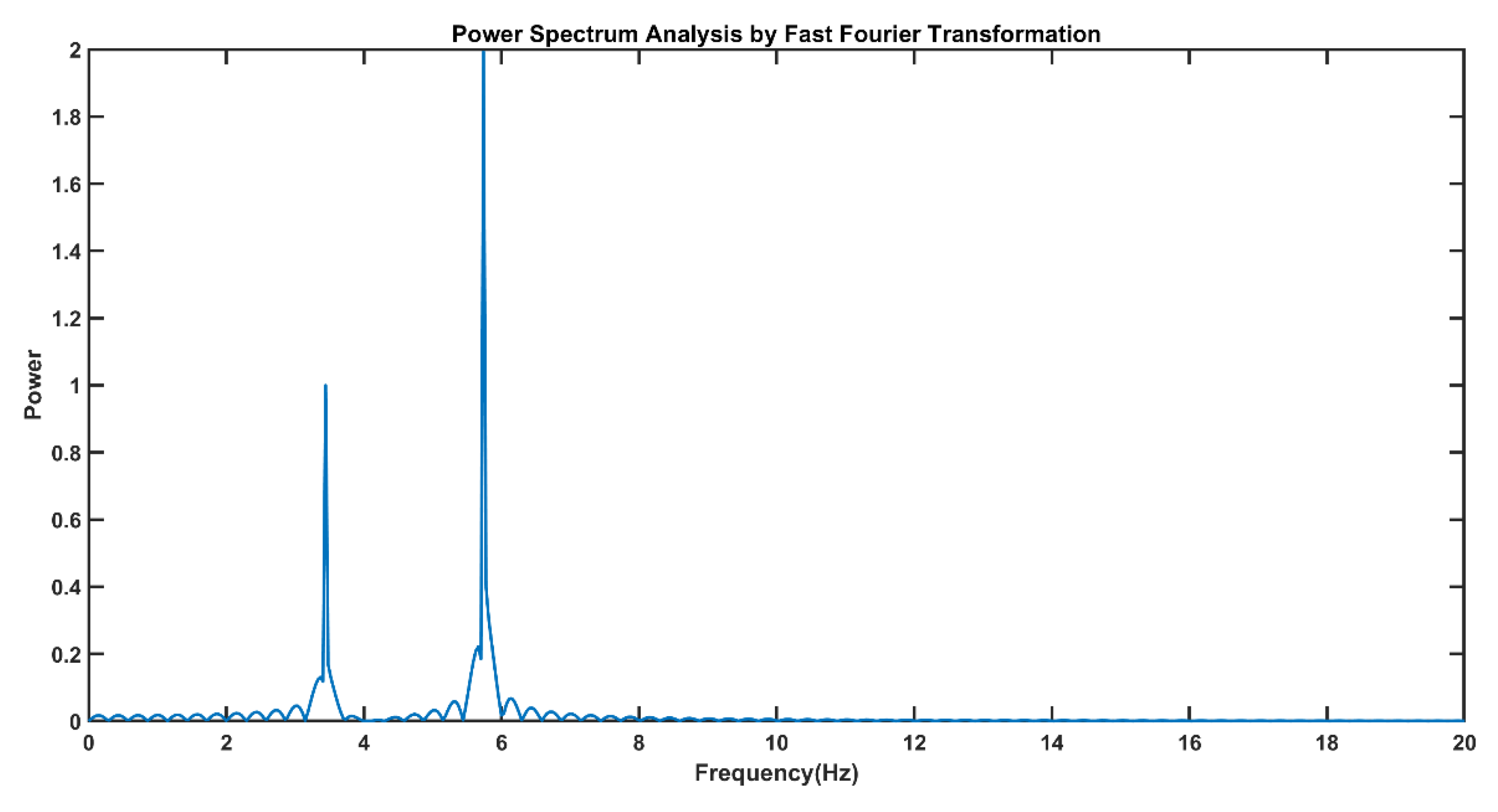

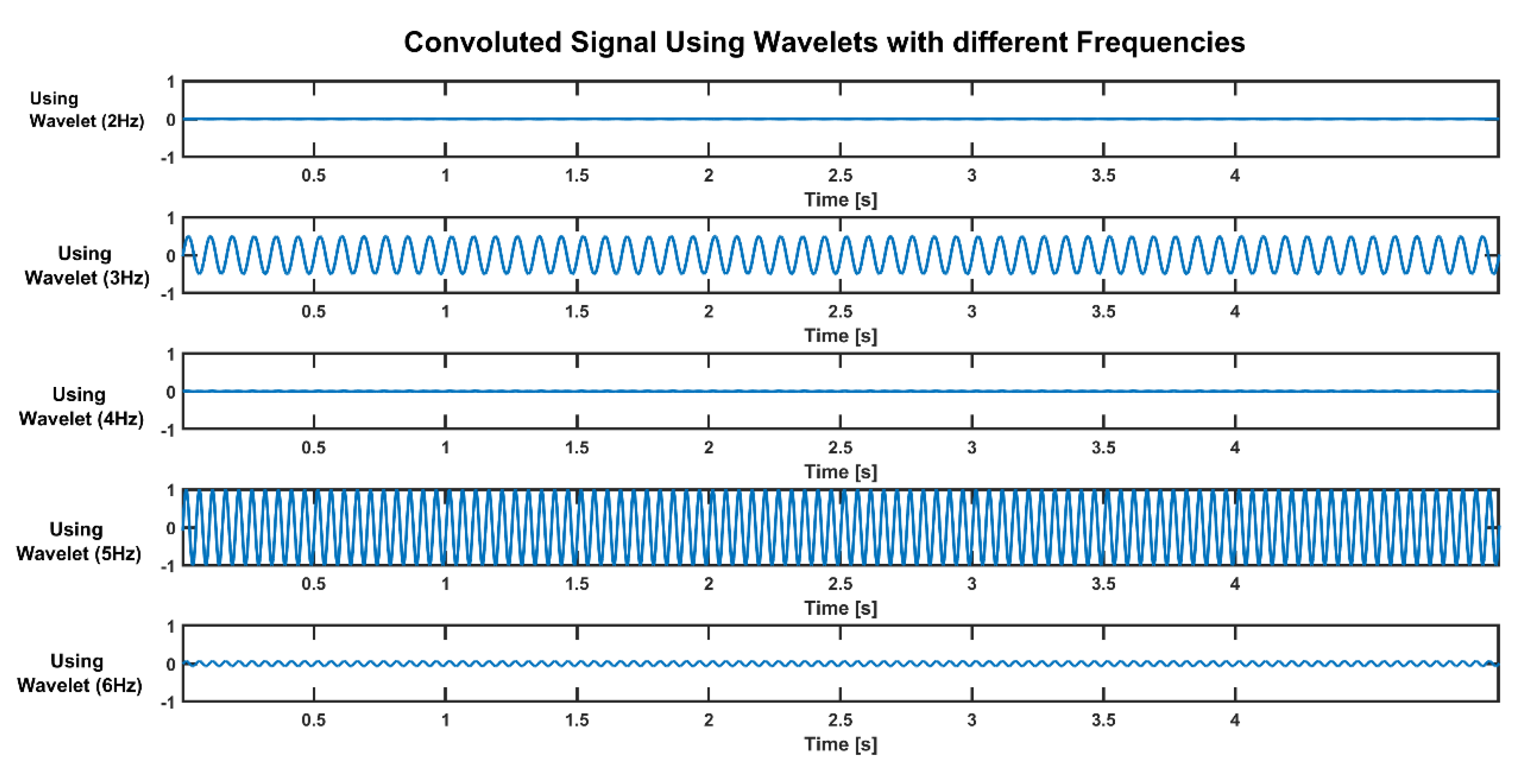




| Parameter | Definition |
|---|---|
| Number_of_Transitions | The total number of transitions found in one sleep dataset. |
| Sleep_Hours | Total number of hours of sleep |
| Transition_Max_Acc | Maximum of acceleration value in each transition |
| Transition_Min_Acc | Minimum of acceleration value in each transition |
| Transition_RMS | Root mean square of acceleration during a transition |
| Transition_Range | Difference between max and min acceleration value in each transition |
| Transition_Duration | Average time for each transition |
| Total Activity Amplitude |
| Low | Medium | High | |||
|---|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | Mean | Standard Deviation |
| m_DRA <0.2 g | std_DRA <0.02 g | 0.2 g < m_DRA < 0.5 g | 0.02 g < std_DRA < 0.2 g | m_DRA >0.5 g | std_DRA >0.2 g |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soangra, R.; Krishnan, V. Wavelet-Based Analysis of Physical Activity and Sleep Movement Data from Wearable Sensors among Obese Adults. Sensors 2019, 19, 3710. https://doi.org/10.3390/s19173710
Soangra R, Krishnan V. Wavelet-Based Analysis of Physical Activity and Sleep Movement Data from Wearable Sensors among Obese Adults. Sensors. 2019; 19(17):3710. https://doi.org/10.3390/s19173710
Chicago/Turabian StyleSoangra, Rahul, and Vennila Krishnan. 2019. "Wavelet-Based Analysis of Physical Activity and Sleep Movement Data from Wearable Sensors among Obese Adults" Sensors 19, no. 17: 3710. https://doi.org/10.3390/s19173710
APA StyleSoangra, R., & Krishnan, V. (2019). Wavelet-Based Analysis of Physical Activity and Sleep Movement Data from Wearable Sensors among Obese Adults. Sensors, 19(17), 3710. https://doi.org/10.3390/s19173710





