Reinforcement Learning-Based End-to-End Parking for Automatic Parking System
Abstract
:1. Introduction
1.1. Related Work
1.1.1. Mainstream APS
1.1.2. Reinforcement Learning
1.2. Objectives and Contributions
- We innovatively apply DDPG to perpendicular parking so that the vehicle can continuously learn and accumulate experience from considerable parking attempts, learn the optimal steering wheel angle command at different parking slots relative to vehicle, as well as achieve the real “human-like” intelligent parking. Moreover, because it realizes the end-to-end control from the parking slot to the steering wheel angle command, the control errors caused by path tracking are fundamentally avoided;
- Since the parking slot needs to be continuously obtained in the course of learning, we propose a parking slot tracking algorithm, which uses extended Kalman filter (EKF) to fuse the parking slot information with vehicle chassis information to achieve continuous tracking of parking slot;
- Given that the learning network output is hard to converge and it is easy to fall into local optimum in the parking process, several reinforcement learning training methods in terms of parking conditions, e.g., manual guided exploration for accumulating initial experience sequence, control cycle phased setting, and training condition phased setting, are designed. Besides, the well-trained network in the simulation environment is migrated to the real vehicle training.
1.3. Paper Outline
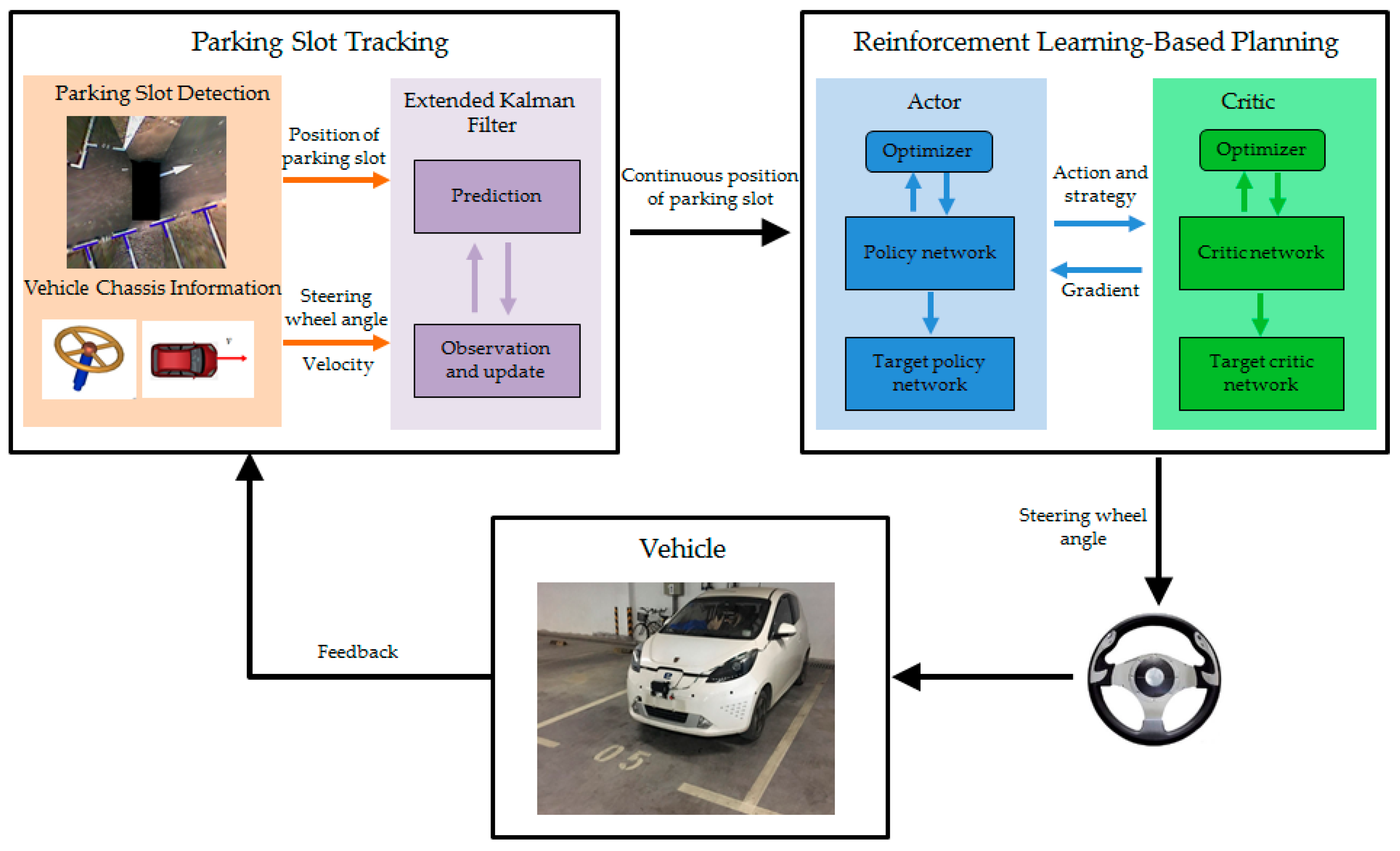
2. Method
2.1. Parking Slot Tracking
2.1.1. Parking Slot Detection
2.1.2. EKF-Based Parking Slot Tracking
2.2. Reinforcement Learning-Based Planning
2.2.1. Appropriate Reinforcement Learning Model for APS
2.2.2. System Settings of DDPG
2.2.3. Training Process of DDPG
| Algorithm 1: DDPG Algorithm |
| Randomly initialize critic network and actor network with parameters and Initialize target critic network and target actor network with parameters and Set up a replay memory buffer (experience pool) for the sampling experience sequence with the total number of buffers for each episode: Initialize a random process for action exploration Receive initial state for :
end for |
2.2.4. Improved Training Measures Applied in Parking
3. Experimental Results
3.1. Experimental Platform
3.2. Experimental Scenes
3.3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- British Standards Institution. BS ISO 16787:2016. Intelligent transport systems-Assisted Parking System (APS)-Performance requirements and test procedures. BSI Standards Limited: UK, 2016. Available online: https://www.iso.org/standard/63626.html (accessed on 10 September 2019).
- Fraichard, T.; Scheuer, A. From reeds and shepp’s to continuous-curvature paths. IEEE Trans. Robot. 2004, 6, 1025–1035. [Google Scholar] [CrossRef]
- Gómez-Bravo, F.; Cuesta, F.; Ollero, A. Parallel and diagonal parking in nonholonomic autonomous vehicles. Eng. Appl. Artif. Intell. 2001, 14, 419–434. [Google Scholar] [CrossRef]
- Lini, G.; Piazzi, A.; Consolini, L. Multi-optimization of η3-splines for autonomous parking. In Proceedings of the 50th IEEE Conference of Decision and Control/European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 6367–6372. [Google Scholar]
- Vorobieva, H.; Minoiu-Enache, N.; Glaser, S.; Mammar, S. Geometric continuous-curvature path planning for automatic parallel parking. In Proceedings of the 2013 IEEE 10th International Conference on Networking, Sensing and Control, Evry, France, 10–12 April 2013; pp. 418–423. [Google Scholar]
- Vorobieva, H.; Glaser, S.; Minoiu-Enache, N.; Mammar, S. Automatic parallel parking in tiny spots: Path planning and control. IEEE Trans. Intell. Transp. Syst. 2015, 16, 396–410. [Google Scholar] [CrossRef]
- Han, L.; Do, Q.H.; Mita, S. Unified path planner for parking an autonomous vehicle based on RRT. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5622–5627. [Google Scholar]
- Zheng, K.; Liu, S. RRT based path planning for autonomous parking of vehicle. In Proceedings of the 2018 IEEE 7th Data Driven Control and Learning Systems Conference, Enshi, China, 25–27 May 2018; pp. 627–632. [Google Scholar]
- Li, B.; Shao, Z. A unified motion planning method for parking an autonomous vehicle in the presence of irregularly placed obstacles. Knowledge-Based Syst. 2015, 86, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Takei, R.; Tsai, R. Optimal trajectories of curvature constrained motion in the Hamilton-jacobi formulation. J. Sci. Comput. 2013, 54, 622–644. [Google Scholar] [CrossRef]
- Micelli, P.; Consolini, L.; Locatelli, M. Path planning with limited numbers of maneuvers for automatic guided vehicles: An optimization-based approach. In Proceedings of the 2017 25th Mediterranean Conference on Control and Automation, Valletta, Malta, 3–6 July 2017; pp. 204–209. [Google Scholar]
- Roald, A.L. Path planning for vehicle motion control using numerical optimization methods. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2015. [Google Scholar]
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D. Stanley: The robot that won the DARPA Grand Challenge. J. Field Robot. 2006, 23, 661–692. [Google Scholar] [CrossRef]
- Park, H.; Ahn, K.; Park, M.; Lee, S. Study on robust lateral controller for differential GPS-based autonomous vehicles. Int. J. Precis. Eng. Manuf. 2018, 19, 367–376. [Google Scholar] [CrossRef]
- Mvemba, P.; Lay-Ekuakille, A.; Kidiamboko, S.; Rahman, M. An embedded beamformer for a PID-based trajectory sensing for an autonomous vehicle. Metrol. Meas. Syst. 2018, 25, 561–575. [Google Scholar]
- He, X.; Liu, Y.; Lv, C.; Ji, X.; Liu, Y. Emergency steering control of autonomous vehicle for collision avoidance and stabilization. Veh. Syst. Dyn. 2019, 57, 1163–1187. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, L.; Zhang, J.; Li, F. Path following control of autonomous ground vehicle based on nonsingular terminal sliding mode and active disturbance rejection control. IEEE Trans. Veh. Technol. 2019, 68, 6379–6390. [Google Scholar] [CrossRef]
- Samuel, M.; Maziah, M.; Hussien, M.; Godi, N. Control of autonomous vehicle using path tracking: A review. In Proceedings of the International Conference on Science, Engineering, Management and Social Sciences, Johor Bahru, Malaysia, 6–8 October 2016; pp. 3877–3879. [Google Scholar]
- Cui, Q.; Ding, R.; Zhou, B.; Wu, X. Path-tracking of an autonomous vehicle via model predictive control and nonlinear filtering. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2018, 232, 1237–1252. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, R.; Xiong, L.; Fu, Z. Robust hierarchical controller with conditional integrator based on small gain theorem for reference trajectory tracking of autonomous vehicles. Veh. Syst. Dyn. 2019, 57, 1143–1162. [Google Scholar] [CrossRef]
- Lidberg, M.; Muller, S. Special issue on motion control for automated driving and autonomous functions on road vehicles. Veh. Syst. Dyn. 2019, 57, 1087–1089. [Google Scholar] [CrossRef]
- Sun, R.; Silver, D.; Tesauro, G.; Huang, G. Introduction to the special issue on deep reinforcement learning: An editorial. Neural Netw. 2018, 107, 1–2. [Google Scholar] [CrossRef] [PubMed]
- Van, H.; Guez, A.; Silver, D. Deep reinforcement learning with double Q-Learning. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 2094–2100. [Google Scholar]
- Sharifzadeh, S.; Chiotellis, I.; Triebel, R.; Cremers, D. Learning to drive using inverse reinforcement learning and Deep Q-Networks. arXiv 2016, arXiv:1612.03653. [Google Scholar]
- Gu, S.; Lillicrap, T.; Ghahramani, Z.; Turner, R.; Levine, S. Q-Prop: Sample-efficient policy gradient with an off-policy critic. arXiv 2016, arXiv:1611.02247. [Google Scholar]
- Jagodnik, K.; Thomas, P.; Branicky, M.; Kirsch, R. Training an Actor-Critic reinforcement learning controller for arm movement using human-generated rewards. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1892–1905. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.; Yang, G.; Ye, D. Quantization-Based Adaptive Actor-Critic Tracking Control With Tracking Error Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 970–980. [Google Scholar] [CrossRef] [PubMed]
- Skach, J.; Kiumarsi, B.; Lewis, F.; Straka, O. Actor-Critic off-policy learning for optimal control of multiple-model discrete-time systems. IEEE T. Cybern. 2018, 48, 29–40. [Google Scholar] [CrossRef]
- Lillicrap, T.; Hunt, J.; Pritzel, A.; Heess, N.; Erez, T. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Xu, J.; Hou, Z.; Wang, W.; Xu, B.; Zhang, K.; Chen, K. Feedback deep deterministic policy gradient with fuzzy reward for robotic multiple peg-in-hole assembly tasks. IEEE Trans. Ind. Inform. 2019, 15, 1658–1667. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Li, L.; Zhang, L.; Li, X.; Liu, X.; Shen, Y.; Xiong, L. Vision-based parking-slot detection: A benchmark and a learning-based approach. In Proceedings of the 2017 IEEE International Conference on Multimedia and Expo, Hong Kong, China, 10–14 July 2017; pp. 649–654. [Google Scholar]
- Imani, M.; Braga-Neto, U. Control of gene regulatory networks using bayesian inverse reinforcement learning. IEEE-ACM Trans. Comput. Biol. Bioinform. 2019, 16, 1250–1261. [Google Scholar] [CrossRef] [PubMed]
- Pan, W.; Qu, R.; Hwang, K.; Lin, H. An ensemble fuzzy approach for inverse reinforcement learning. Int. J. Fuzzy Syst. 2019, 21, 95–103. [Google Scholar] [CrossRef]
- Gao, C.; Yan, J.; Zhou, S.; Chen, B.; Liu, H. Long short-term memory-based recurrent neural networks for nonlinear target tracking. Signal Process. 2019, 164, 67–73. [Google Scholar] [CrossRef]






















| Planned Path | Planned Path+PID | Planned Path+SMC | Reinforcement Learning | |
|---|---|---|---|---|
| Inclination angle β (°) | −1.051 | −3.638 | −3.126 | −0.747 |
| Deviation dfr (m) | 0.423 | 0.304 | 0.379 | 0.457 |
| Deviation dfl (m) | 0.468 | 0.589 | 0.514 | 0.463 |
| Deviation drr (m) | 0.465 | 0.45 | 0.504 | 0.487 |
| Deviation drl (m) | 0.425 | 0.443 | 0.388 | 0.434 |
| Deviation de (m) | 1.087 | 1.016 | 1.047 | 1.053 |
| X average error (m) | \ | 0.021 | 0.028 | \ |
| Y average error (m) | \ | 0.033 | 0.048 | \ |
| Loss rate of visual detection (%) | \ | \ | \ | 37.35 |
| Loss rate of parking slot tracking (%) | \ | \ | \ | 0 |
| Planned Path | Planned Path+PID | Planned Path+SMC | Reinforcement Learning | |
|---|---|---|---|---|
| Inclination angle β (°) | 0.313 | 3.088 | 2.011 | −0.573 |
| Deviation dfr (m) | 0.493 | 0.557 | 0.59 | 0.438 |
| Deviation dfl (m) | 0.377 | 0.315 | 0.281 | 0.436 |
| Deviation drr (m) | 0.48 | 0.433 | 0.509 | 0.461 |
| Deviation drl (m) | 0.391 | 0.439 | 0.361 | 0.413 |
| Deviation de (m) | 0.872 | 0.788 | 0.795 | 0.918 |
| X average error (m) | \ | 0.032 | 0.042 | \ |
| Y average error (m) | \ | 0.024 | 0.019 | \ |
| Loss rate of visual detection (%) | \ | \ | \ | 43.68 |
| Loss rate of parking slot tracking (%) | \ | \ | \ | 0 |
| Planned Path | Planned Path+PID | Planned Path+SMC | Reinforcement Learning | |
|---|---|---|---|---|
| Inclination angle β (°) | −0.223 | −3.782 | 2.416 | −1.02 |
| Deviation dfr (m) | 0.394 | 0.363 | 0.552 | 0.376 |
| Deviation dfl (m) | 0.456 | 0.49 | 0.299 | 0.474 |
| Deviation drr (m) | 0.403 | 0.515 | 0.455 | 0.417 |
| Deviation drl (m) | 0.447 | 0.339 | 0.396 | 0.434 |
| Deviation de (m) | 1.031 | 0.952 | 0.948 | 1.056 |
| X average error (m) | \ | 0.056 | 0.043 | \ |
| Y average error (m) | \ | 0.028 | 0.031 | \ |
| Loss rate of visual detection (%) | \ | \ | \ | 31.48 |
| Loss rate of parking slot tracking (%) | \ | \ | \ | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Xiong, L.; Yu, Z.; Fang, P.; Yan, S.; Yao, J.; Zhou, Y. Reinforcement Learning-Based End-to-End Parking for Automatic Parking System. Sensors 2019, 19, 3996. https://doi.org/10.3390/s19183996
Zhang P, Xiong L, Yu Z, Fang P, Yan S, Yao J, Zhou Y. Reinforcement Learning-Based End-to-End Parking for Automatic Parking System. Sensors. 2019; 19(18):3996. https://doi.org/10.3390/s19183996
Chicago/Turabian StyleZhang, Peizhi, Lu Xiong, Zhuoping Yu, Peiyuan Fang, Senwei Yan, Jie Yao, and Yi Zhou. 2019. "Reinforcement Learning-Based End-to-End Parking for Automatic Parking System" Sensors 19, no. 18: 3996. https://doi.org/10.3390/s19183996
APA StyleZhang, P., Xiong, L., Yu, Z., Fang, P., Yan, S., Yao, J., & Zhou, Y. (2019). Reinforcement Learning-Based End-to-End Parking for Automatic Parking System. Sensors, 19(18), 3996. https://doi.org/10.3390/s19183996




