Optimal Message Bundling with Delay and Synchronization Constraints in Wireless Sensor Networks
Abstract
:1. Introduction
2. Preliminaries
2.1. Existing Methods toward Improving Energy Efficiency
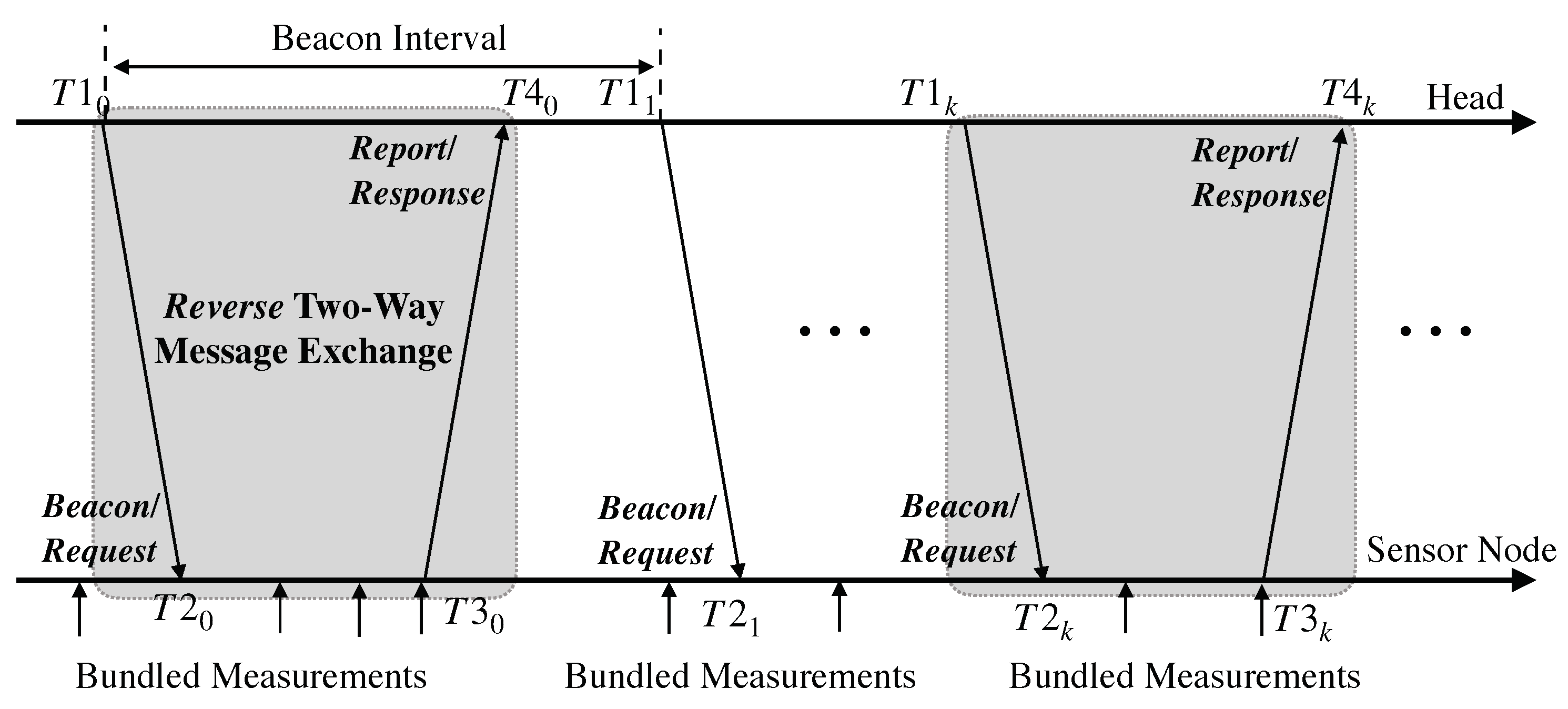
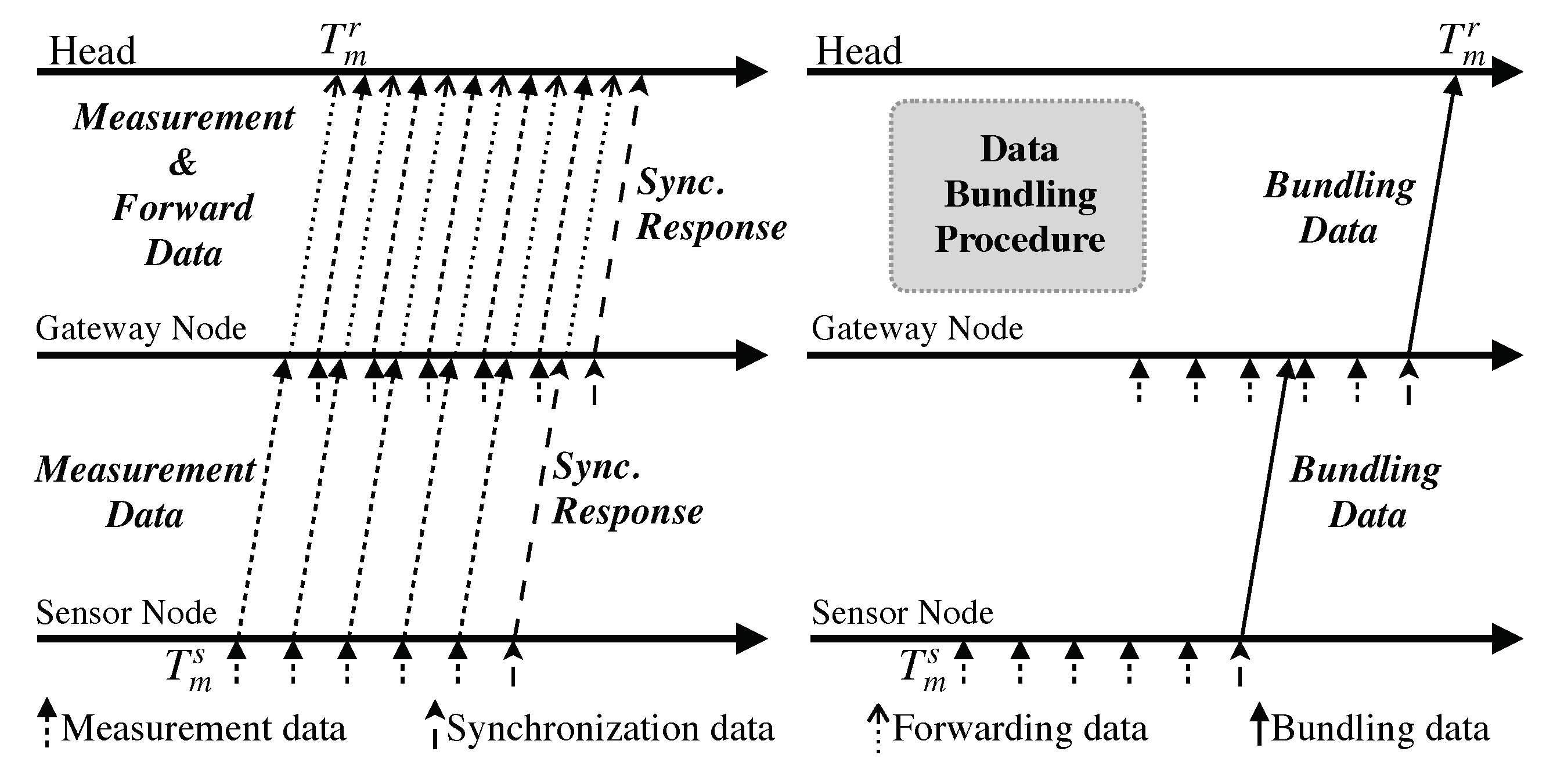
2.2. Energy-Efficient Time Synchronization Schemes Using Data Bundling
2.3. Conflicts of Performance Metrics: Energy Efficiency, E2E Delay and Synchronization Accuracy
3. ILP Model for the Optimal Bundling Problem
3.1. Maximization of Bundling Number for Energy Efficiency
3.2. Constraining E2E Delay
3.3. Constraining Synchronization Accuracy
3.4. ILP Model
4. System Design
4.1. Performance Maintainer at Head
4.2. Parameter Adapter at Sensor Nodes
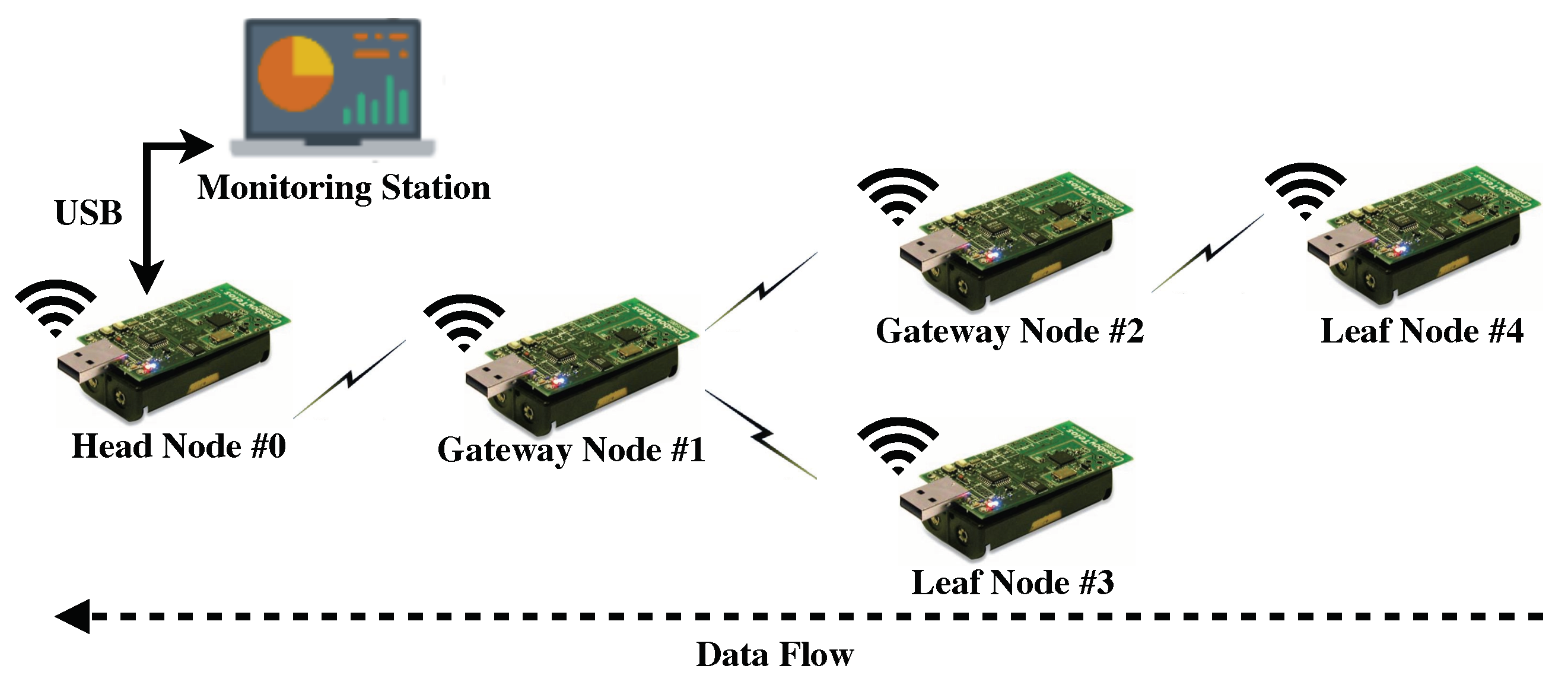
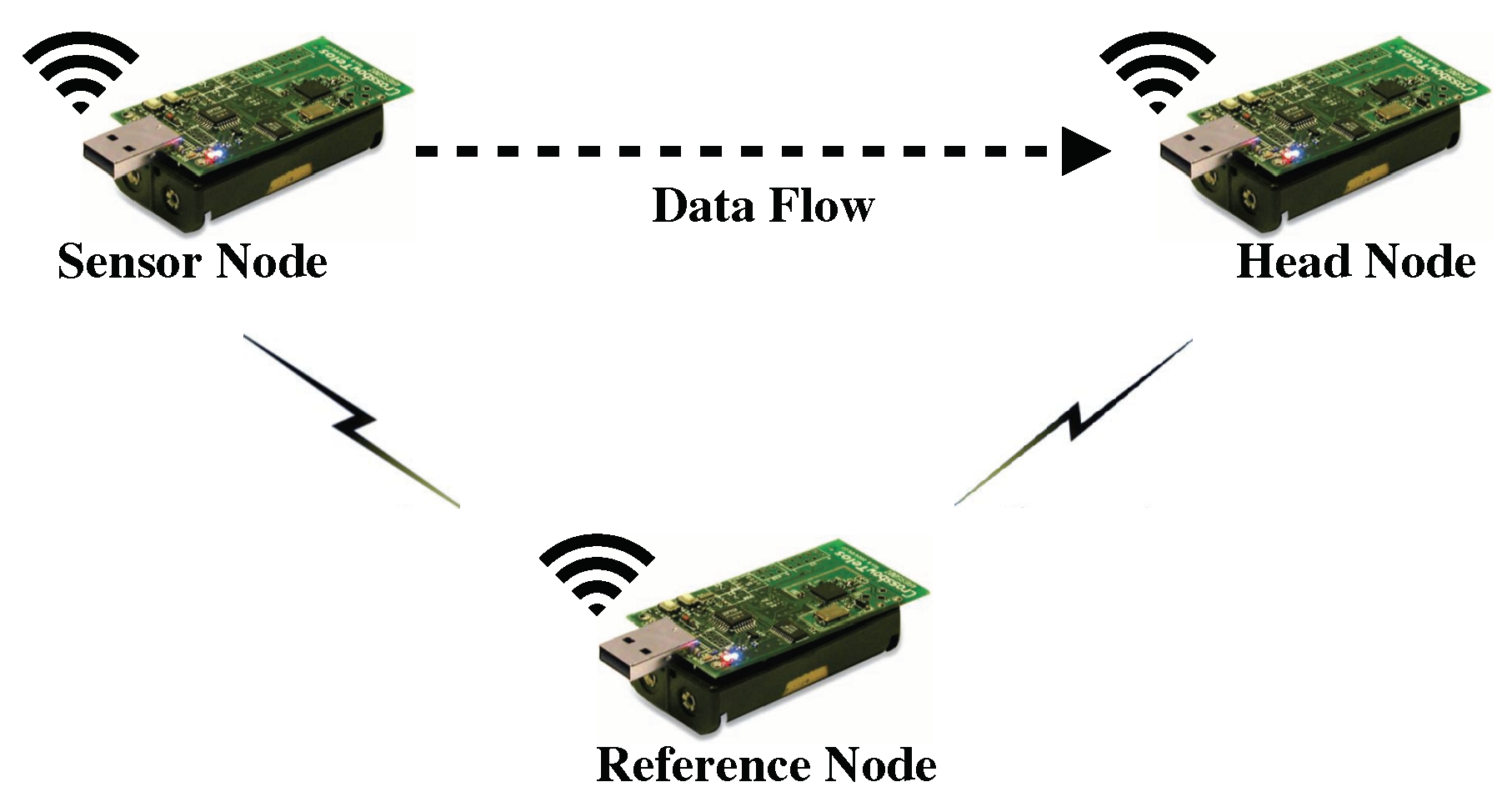
5. Experimental Results
5.1. Delay Performance under Static Requirement Setting
5.2. Delay Performance under Dynamic Requirement Setting
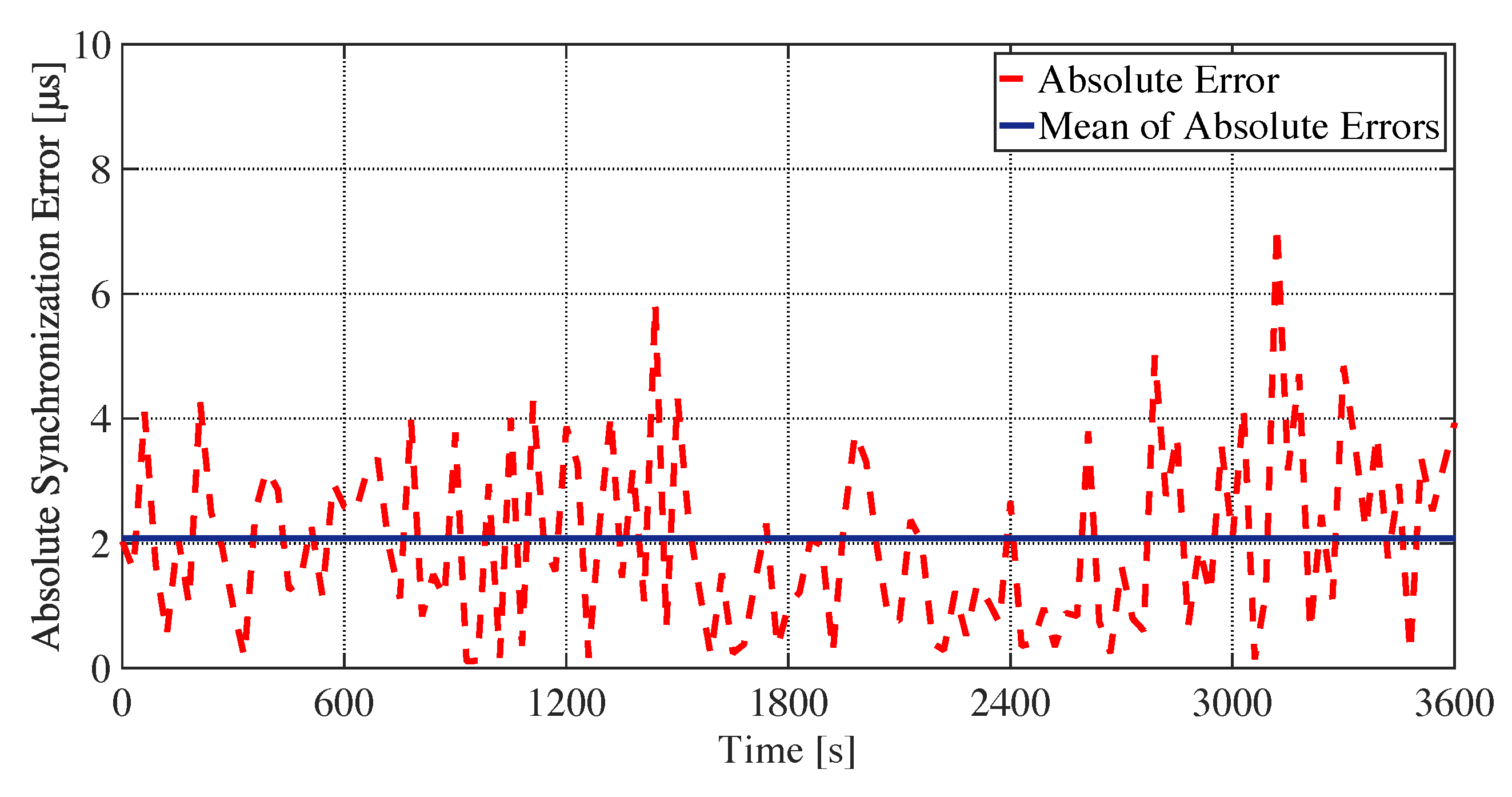
5.3. Synchronization Accuracy
5.4. Energy Efficiency
5.5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, K.S.; Lee, S.; Lim, E.G. Energy-Efficient Time Synchronization Based on Asynchronous Source Clock Frequency Recovery and Reverse Two-Way Message Exchanges in Wireless Sensor Networks. IEEE Trans. Commun. 2017, 65, 347–359. [Google Scholar] [CrossRef]
- Cui, J.; Valois, F. Data Aggregation in Wireless Sensor Networks: Compressing or Forecasting? In Proceedings of the 2014 IEEE Wireless Communications and Networking Conference (WCNC), Istanbul, Turkey, 6–9 April 2014; pp. 2892–2897. [Google Scholar] [CrossRef]
- Rajagopalan, R.; Varshney, P.K. Data-aggregation techniques in sensor networks: A survey. IEEE Commun. Surv. Tutor. 2006, 8, 48–63. [Google Scholar] [CrossRef]
- Li, X.; Liu, W.; Xie, M.; Liu, A.; Zhao, M.; Xiong, N.N.; Zhao, M.; Dai, W. Differentiated Data Aggregation Routing Scheme for Energy Conserving and Delay Sensitive Wireless Sensor Networks. Sensors 2018, 18. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, A.; Xie, M.; Xiong, N.N.; Zeng, Z.; Cai, Z. Adaptive Aggregation Routing to Reduce Delay for Multi-Layer Wireless Sensor Networks. Sensors 2018, 18. [Google Scholar] [CrossRef] [PubMed]
- Villas, L.A.; Boukerche, A.; Ramos, H.S.; de Oliveira, H.A.B.F.; de Araujo, R.B.; Loureiro, A.A.F. DRINA: A Lightweight and Reliable Routing Approach for In-Network Aggregation in Wireless Sensor Networks. IEEE Trans. Comput. 2013, 62, 676–689. [Google Scholar] [CrossRef]
- Bahi, J.M.; Makhoul, A.; Medlej, M. An Optimized In-Network Aggregation Scheme for Data Collection in Periodic Sensor Networks. In Ad-Hoc, Mobile, and Wireless Networks, Proceedings of the 11th International Conference, ADHOC-NOW 2012, Belgrade, Serbia, 9–11 July 2012; Spring: Berlin/Heidelberg, Germany, 2012; pp. 153–166. [Google Scholar]
- Intanagonwiwat, C.; Estrin, D.; Govindan, R.; Heidemann, J. Impact of Network Density on Data Aggregation in Wireless Sensor Networks. In Proceedings of the IEEE 22nd International Conference on Distributed Computing Systems, Vienna, Austria, 2–5 July 2002; pp. 457–458. [Google Scholar] [CrossRef]
- Madden, S.; Franklin, M.J.; Hellerstein, J.M.; Hong, W. The Design of an Acquisitional Query Processor for Sensor Networks. In Proceedings of the 2003 ACM SIGMOD International Conference on Management of Data, San Diego, CA, USA, 9–12 June 2003; pp. 491–502. [Google Scholar]
- Atoui, I.; Ahmad, A.; Medlej, M.; Makhoul, A.; Tawbe, S.; Hijazi, A. Tree-Based Data Aggregation approach in Wireless Sensor Network Using Fitting Functions. In Proceedings of the 2016 Sixth International Conference on Digital Information Processing and Communications (ICDIPC), Beirut, Lebanon, 21–23 April 2016; pp. 146–150. [Google Scholar] [CrossRef]
- Xu, X.; Li, X.Y.; Mao, X.; Tang, S.; Wang, S. A Delay-Efficient Algorithm for Data Aggregation in Multihop Wireless Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2011, 22, 163–175. [Google Scholar] [CrossRef]
- YOSHINO, H.; OTA, K.; HIRAGURI, T. Queueing Delay Analysis and Optimization of Statistical Data Aggregation and Transmission Systems. IEICE Trans. Commun. 2018, E101.B, 2186–2195. [Google Scholar] [CrossRef]
- Deng, X.; Yang, Y. Online Adaptive Compression in Delay Sensitive Wireless Sensor Networks. IEEE Trans. Comput. 2012, 61, 1429–1442. [Google Scholar] [CrossRef]
- Al-Anbagi, I.; Erol-Kantarci, M.; Mouftah, H.T. Delay Critical Smart Grid Applications and Adaptive QoS Provisioning. IEEE Access 2015, 3, 1367–1378. [Google Scholar] [CrossRef]
- Doudou, M.; Djenouri, D.; Badache, N. Survey on Latency Issues of Asynchronous MAC Protocols in Delay-Sensitive Wireless Sensor Networks. IEEE Commun. Surv. Tutor. 2013, 15, 528–550. [Google Scholar] [CrossRef]
- Wang, Y.; Vuran, M.C.; Goddard, S. Cross-Layer Analysis of the End-to-End Delay Distribution in Wireless Sensor Networks. IEEE/ACM Trans. Netw. 2012, 20, 305–318. [Google Scholar] [CrossRef]
- Wang, J.; Dong, W.; Cao, Z.; Liu, Y. On the Delay Performance in a Large-Scale Wireless Sensor Network: Measurement, Analysis, and Implications. IEEE/ACM Trans. Netw. 2015, 23, 186–197. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.; Guo, X.; Gao, M.; Ming, Z.; Yang, L.; Ni, L.M. RSS-Based Ranging by Leveraging Frequency Diversity to Distinguish the Multiple Radio Paths. IEEE Trans. Mob. Comput. 2017, 16, 1121–1135. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, Y.; Guo, X.; Ni, L.M. RASS: A Real-Time, Accurate, and Scalable System for Tracking Transceiver-Free Objects. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 996–1008. [Google Scholar] [CrossRef]
- Kim, B.; Hong, S.; Hur, K.; Eom, D. Energy-efficient and rapid time synchronization for wireless sensor networks. IEEE Trans. Consum. Electron. 2010, 56, 2258–2266. [Google Scholar] [CrossRef]
- Gong, F.; Sichitiu, M.L. CESP: A Low-Power High-Accuracy Time Synchronization Protocol. IEEE Trans. Veh. Technol. 2016, 65, 2387–2396. [Google Scholar] [CrossRef]
- Nadas, J.P.B.; Souza, R.D.; Pellenz, M.E.; Brante, G.; Braga, S.M. Energy Efficient Beacon Based Synchronization for Alarm Driven Wireless Sensor Networks. IEEE Signal Process. Lett. 2016, 23, 336–340. [Google Scholar] [CrossRef]
- Al-Shaikhi, A.; Masoud, A. Efficient, Single Hop Time Synchronization Protocol for Randomly Connected WSNs. IEEE Wirel. Commun. Lett. 2017, 6, 170–173. [Google Scholar] [CrossRef] [Green Version]
- Tavares Bruscato, L.; Heimfarth, T.; Pignaton de Freitas, E. Enhancing Time Synchronization Support in Wireless Sensor Networks. Sensors 2017, 17. [Google Scholar] [CrossRef]
- Wang, Y.; Nunez, F.; Doyle, F.J. Energy-Efficient Pulse-Coupled Synchronization Strategy Design for Wireless Sensor Networks Through Reduced Idle Listening. IEEE Trans. Signal Process. 2012, 60, 5293–5306. [Google Scholar] [CrossRef] [Green Version]
- Akhlaq, M.; Sheltami, T.R. RTSP: An Accurate and Energy-Efficient Protocol for Clock Synchronization in WSNs. IEEE Trans. Instrum. Meas. 2013, 62, 578–589. [Google Scholar] [CrossRef]
- Vieira, M.A.M.; Coelho, C.N.; da Silva, D.C.; da Mata, J.M. Survey on Wireless Sensor Network Devices. In Proceedings of the 2003 IEEE Conference on Emerging Technologies and Factory Automation, Lisbon, Portugal, 16–19 September 2003; pp. 537–544. [Google Scholar]
- Lin, S.; Miao, F.; Zhang, J.; Zhou, G.; Gu, L.; He, T.; Stankovic, J.A.; Son, S.; Pappas, G.J. ATPC: Adaptive Transmission Power Control for Wireless Sensor Networks. ACM Trans. Sen. Netw. 2016, 12, 6:1–6:31. [Google Scholar] [CrossRef]
- Chincoli, M.; Liotta, A. Self-Learning Power Control in Wireless Sensor Networks. Sensors 2018, 18. [Google Scholar] [CrossRef] [PubMed]
- Pal, A.; Nasipuri, A. Joint Power Control and Routing for Rechargeable Wireless Sensor Networks. IEEE Access 2019, 123992–124007. [Google Scholar] [CrossRef]
- Chipara, O.; He, Z.; Xing, G.; Chen, Q.; Wang, X.; Lu, C.; Stankovic, J.; Abdelzaher, T. Real-Time Power-Aware Routing in Sensor Networks. In Proceedings of the 2006 14th IEEE International Workshop on Quality of Service, New Haven, CT, USA, 19–21 June 2006; pp. 83–92. [Google Scholar] [CrossRef]
- Wu, Y.; Stankovic, J.A.; He, T.; Lin, S. Realistic and Efficient Multi-Channel Communications in Wireless Sensor Networks. In Proceedings of the IEEE INFOCOM 2008—The 27th Conference on Computer Communications, Phoenix, AZ, USA, 13–18 April 2008; pp. 1193–1201. [Google Scholar] [CrossRef]
- Pal, A.; Nasipuri, A. Distributed Routing and Channel Selection for Multi-Channel Wireless Sensor Networks. J. Sens. Actuator Netw. 2017, 6. [Google Scholar] [CrossRef]
- Abdeddaim, N.; Theoleyre, F.; Heusse, M.; Duda, A. Adaptive IEEE 802.15.4 MAC for Throughput and Energy Optimization. In Proceedings of the 2013 IEEE International Conference on Distributed Computing in Sensor Systems, Cambridge, MA, USA, 20–23 May 2013; pp. 223–230. [Google Scholar] [CrossRef]
- Zlmmerling, M.; Ferrari, F.; Mottola, L.; Voigt, T.; Thiele, L. pTUNES: Runtime Parameter Adaptation for Low-power MAC Protocols. In Proceedings of the 2012 ACM/IEEE 11th International Conference on Information Processing in Sensor Networks (IPSN), Beijing, China, 16–20 April 2012; pp. 173–184. [Google Scholar] [CrossRef]
- Noda, C.; Prabh, S.; Alves, M.; Voigt, T. On Packet Size and Error Correction Optimisations in Low-power Wireless Networks. In Proceedings of the 2013 IEEE International Conference on Sensing, Communications and Networking (SECON), New Orleans, LA, USA, 24–27 June 2013; pp. 212–220. [Google Scholar] [CrossRef]
- Dong, W.; Chen, C.; Liu, X.; He, Y.; Liu, Y.; Bu, J.; Xu, X. Dynamic Packet Length Control in Wireless Sensor Networks. IEEE Trans. Wirel. Commun. 2014, 13, 1172–1181. [Google Scholar] [CrossRef]
- Pal, A.; Kant, K. On the Feasibility of Distributed Sampling Rate Adaptation in Heterogeneous and Collaborative Wireless Sensor Networks. In Proceedings of the 2016 25th International Conference on Computer Communication and Networks (ICCCN), Waikoloa, HI, USA, 1–4 August 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, Y.; Jiang, Y.; Hu, C.; Shih, C.; Marrón, P.J. Experimental Study for Multi-layer Parameter Configuration of WSN Links. In Proceedings of the IEEE 35th International Conference on Distributed Computing Systems, Columbus, OH, USA, 29 June–2 July 2015; pp. 369–378. [Google Scholar] [CrossRef]
- Battestilli, T.; Perros, H. An introduction to optical burst switching. IEEE Commun. Mag. 2003, 41, S10–S15. [Google Scholar] [CrossRef]
- Pal, A.; Kant, K. E-Darwin2: A Smartphone Based Disaster Recovery Network Using WiFi Tethering. In Proceedings of the 2018 15th IEEE Annual Consumer Communications Networking Conference (CCNC), Las Vegas, NV, USA, 12–15 January 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Kim, K.S. Asynchronous Source Clock Frequency Recovery through Aperiodic Packet Streams. IEEE Commun. Lett. 2013, 17, 1455–1458. [Google Scholar] [CrossRef] [Green Version]
- Huan, X.; Kim, K.S. On the Practical Implementation of Propagation Delay and Clock Skew Compensated High-Precision Time Synchronization Schemes with Resource-Constrained Sensor Nodes in Multi-Hop Wireless Sensor Networks. arXiv 2019, arXiv:1905.00554. [Google Scholar]
- Elson, J.; Girod, L.; Estrin, D. Fine-Grained Network Time Synchronization Using Reference Broadcasts. In Proceedings of the 5th Symposium on Operating Systems Design and Implementation, New York, NY, USA, 9–11 December 2002; pp. 147–163. [Google Scholar]







| Synchronization Scheme | MAE 1 | MSE 2 | |
|---|---|---|---|
| EE-ASCFR | SI | 8.8811 × 10 | 5.8990× 10 |
| SI | 9.1748 × 10 | 5.4210 × 10 | |
| SI | 1.0887 × 10 | 4.7684 × 10 | |
| AHTS | SI | 8.4225 × 10 | 1.2524 × 10 |
| SI | 2.3385 × 10 | 9.1694 × 10 | |
| SI | 1.8166 × 10 | 5.2094 × 10 | |
| Max Bundling Number | E2E Delay Requirement (s) | Optimal Bundling Number | |||
|---|---|---|---|---|---|
| Node 1 | Node 2 | Node 3 | Node 4 | ||
| 15 | 14 | 15 | 14 | 8 | 1 |
| 15 | 10 | 15 | 10 | 6 | 1 |
| 15 | 8 | 15 | 6 | 4 | 1 |
| 15 | 6 | 15 | 2 | 2 | 1 |
| 15 | 4 | 14 | 1 | 1 | 1 |
| 15 | 1 | 1 | 1 | 1 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huan, X.; Kim, K.S.; Lee, S.; Kim, M.K. Optimal Message Bundling with Delay and Synchronization Constraints in Wireless Sensor Networks. Sensors 2019, 19, 4027. https://doi.org/10.3390/s19184027
Huan X, Kim KS, Lee S, Kim MK. Optimal Message Bundling with Delay and Synchronization Constraints in Wireless Sensor Networks. Sensors. 2019; 19(18):4027. https://doi.org/10.3390/s19184027
Chicago/Turabian StyleHuan, Xintao, Kyeong Soo Kim, Sanghyuk Lee, and Moon Keun Kim. 2019. "Optimal Message Bundling with Delay and Synchronization Constraints in Wireless Sensor Networks" Sensors 19, no. 18: 4027. https://doi.org/10.3390/s19184027
APA StyleHuan, X., Kim, K. S., Lee, S., & Kim, M. K. (2019). Optimal Message Bundling with Delay and Synchronization Constraints in Wireless Sensor Networks. Sensors, 19(18), 4027. https://doi.org/10.3390/s19184027






