DOA Tracking Based on Unscented Transform Multi-Bernoulli Filter in Impulse Noise Environment
Abstract
:1. Introduction
2. Problem Formulation
2.1. Array Signal Model
2.2. α Stable Distribution
3. MeMBer Bayesian Theory of DOA Tracking
3.1. Multi-Target Bayesian Theory
3.2. Multi-Target Multi-Bernoulli Filter
4. Improved Algorithm for Likelihood Function
5. UT-MeMBer DOA Particle Filter Tracking Algorithm
| Algorithm 1 UT-MeMBer DOA particle filter tracking algorithm | |
| Input: | |
| Time Update | |
| 1. | Predict the existence probability: . |
| where denotes the existence probability of survival model, represents the existence probability of newborn model. | |
| 2. | Calculate the predicted state of surviving particles: . |
| -Calculate the array flow matrix ; | |
| -Calculate the amplitude of the signal ; | |
| -Calculate the noise variance ; | |
| -Select a weighted sample point of
for each particle , where , is a secondary scaling parameter, . | |
| -Each sigma point propagates through a nonlinear function: ; | |
| -Compute the mean and covariance of : ; | |
| -Obtain: ; | |
| 3. | Construct a newborn target weighted particle: . |
| 4. | Calculate the prediction weight according to (26). |
| 5. | Unite weighted particle set: where , . |
| Measurements Update | |
| 6. | For each particle , Calculate the likelihood function according to (28). |
| 7. | Update existence probability: . where . |
| 8. | The updated weight is calculated by (27) and normalized . |
| Resample Step | |
| 9. | . |
| Output: . | |
6. Simulation Results
6.1. Scenario 1: The Number of Targets Is Not Time-Varying
6.2. Scenario 2: The Number of Targets Is Time-Varying
6.3. Scenario 3: The Number of Targets Is Time-Varying and Maneuvering
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, H.; Viberg, M. Two decades of array signal processing research. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar]
- Van Trees, H.L. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Zhou, C.; Gu, Y.; Fan, X.; Shi, Z.; Mao, G.; Zhang, Y.D. Direction-of-Arrival Estimation for Coprime Array via Virtual Array Interpolation. IEEE Trans. Signal Process. 2018, 22, 5956–5971. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Shi, Z.; Zhang, Y.D. Off-Grid Direction-of-Arrival Estimation Using Coprime Array Interpolation. IEEE Signal Process. Lett. 2018, 25, 1710–1714. [Google Scholar] [CrossRef]
- Shi, Z.; Zhou, C.; Gu, Y.; Goodman, N.A.; Qu, F. Source estimation using coprime array: A sparse reconstruction perspective. IEEE Sens. J. 2017, 17, 755–765. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Zhang, Y.D.; Shi, Z.; Jin, T.; Wu, X. Compressive Sensing based Coprime Array Direction-of-Arrival Estimation. IET Commun. 2017, 11, 1719–1724. [Google Scholar] [CrossRef]
- Yang, B. Projection approximation subspace tracking. IEEE Trans. Signal Process. 1995, 43, 95–107. [Google Scholar] [CrossRef]
- Yang, B. Convergence analysis of the subspace tracking algorithms PAST and PASTD. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Atlanta, GA, USA, 9 May 1996; pp. 1759–1762. [Google Scholar]
- Chan, S.C.; Wen, Y.; Ho, K.L. A robust past algorithm for subspace tracking in impulsive noise. IEEE Trans. Signal Process. 2006, 54, 105–116. [Google Scholar] [CrossRef]
- Liao, B.; Zhang, Z.G.; Chan, S.C. A New Robust Kalman Filter-Based Subspace Tracking Algorithm in an Impulsive Noise Environment. IEEE Trans. Circuits Syst. II Express Briefs 2010, 57, 740–744. [Google Scholar] [CrossRef] [Green Version]
- Chan, S.C.; Zhang, Z.G.; Zhou, Y. A new adaptive Kalman filter-based subspace tracking algorithm and its application to DOA estimation. In Proceedings of the IEEE International Symposium on Circuits and Systems, Island of Kos, Greece, 21–24 May 2006; pp. 129–132. [Google Scholar]
- Nikias, C.L.; Shao, M. Signal Processing with Alpha-Stable Distributions and Applications; John Wiley and Sons Inc.: Hoboken, NJ, USA, 1995; pp. 10–15. [Google Scholar]
- Zha, D.; Qiu, T. Underwater sources location in non-Gaussian impulsive noise environments. Digit. Signal Process. 2006, 16, 149–163. [Google Scholar] [CrossRef]
- Shao, M.; Nikias, C.L. Signal processing with fractional lower order moments: Stable processes and their applications. IEEE Proc. 1993, 81, 986–1010. [Google Scholar] [CrossRef]
- Li, S.; He, R.; Lin, B.; Sun, F. DOA estimation based on sparse representation of the fractional lower order statistics in impulsive noise. IEEE CAA J. Autom. Sin. 2018, 5, 98–106. [Google Scholar] [CrossRef]
- Shi, Y.; Mao, X.P.; Qian, C.; Liu, Y.T. Robust relaxation for coherent DOA estimation in impulsive noise. IEEE Signal Process. Lett. 2019, 3, 410–414. [Google Scholar] [CrossRef]
- Zhang, J.; Qiu, T. A robust correntropy based subspace tracking algorithm in impulsive noise environments. Digit. Signal Process. 2017, 62, 168–175. [Google Scholar] [CrossRef]
- Risfic, B.; Arulampalam, S.; Gordon, N. Beyond the Kalman Filter: Particle Filters for Tacking Application; Artech House: London, UK, 2004; pp. 35–62. [Google Scholar]
- Zhong, X.; Premkumar, A.B.; Madhukumar, A.S. Particle filtering for acoustic source tracking in impulsive noise with alpha-stable process. IEEE Sens. J. 2012, 13, 589–600. [Google Scholar] [CrossRef]
- Mahler, R. Statistical Multi-Source Multi-Target Information Fusion; Artech House, Inc.: London, UK, 2007; pp. 228–234. [Google Scholar]
- Ristic, B.; Vo, B.T.; Vo, B.N.; Farina, A. A Tutorial on Bernoulli Filters: Theory, Implementation and Applications. IEEE Trans. Signal Process. 2013, 61, 3406–3430. [Google Scholar] [CrossRef]
- Zhang, G.; Zheng, C.; Sun, S.; Liang, G.; Zhang, Y. Joint Detection and DOA Tracking with a Bernoulli Filter Based on Information Theoretic Criteria. Sensors 2018, 18, 3473. [Google Scholar] [CrossRef] [PubMed]
- Vo, B.T.; Vo, B.N.; Cantoni, A. The cardinality balanced multi-target Multi-Bernoulli filter and its implementations. IEEE Trans. Signal Process. 2009, 57, 409–423. [Google Scholar]
- Choppala, P.B.; Teal, P.D.; Frean, M.R. Adapting the Multi-Bernoulli filter to phased array observations using MUSIC as pseudo-likelihood. In Proceedings of the International Conference on Information Fusion, Salamanca, Spain, 7–10 July 2014; pp. 1–6. [Google Scholar]
- Tsakalides, P.; Nikias, C.L. The robust covariation-based MUSIC (ROC-MUSIC) algorithm for bearing estimation in impulsive noise environments. IEEE Trans. Signal Process. 2002, 44, 1623–1633. [Google Scholar] [CrossRef]
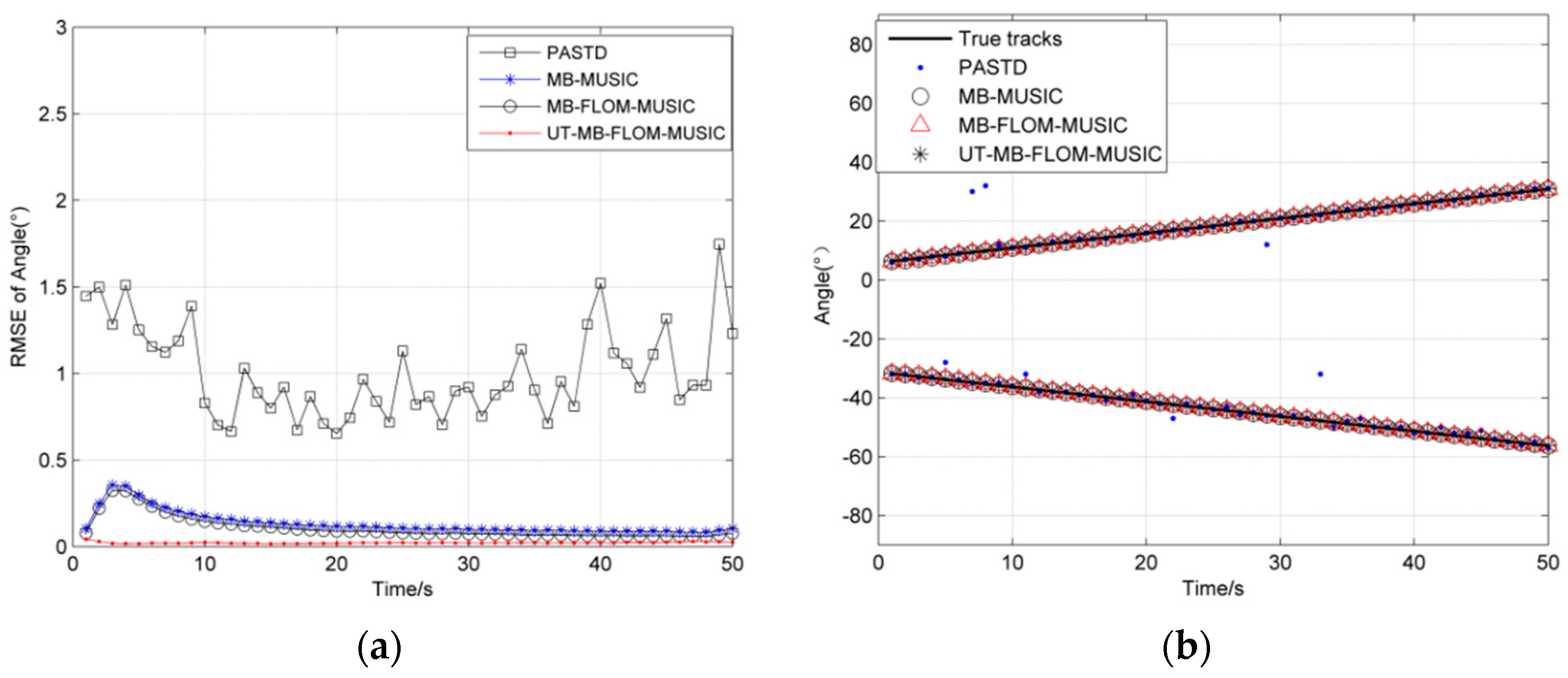
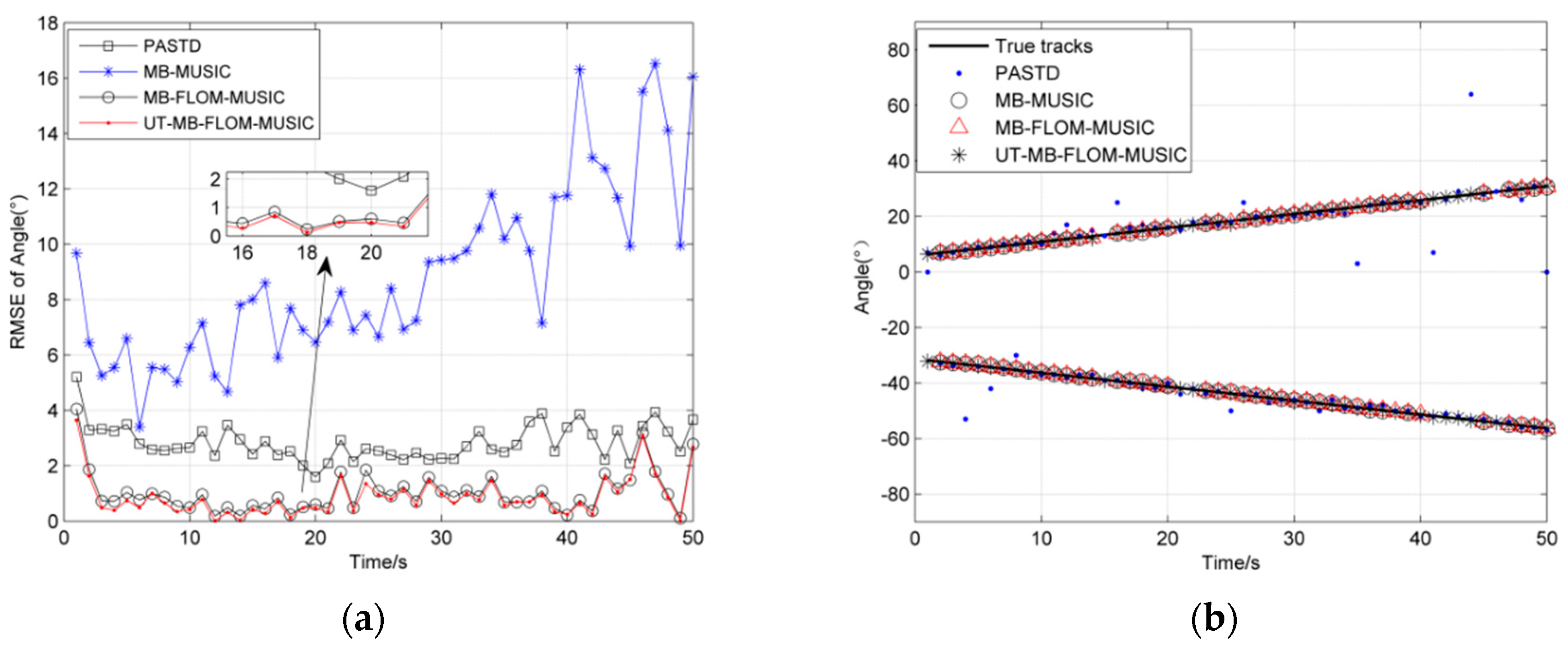
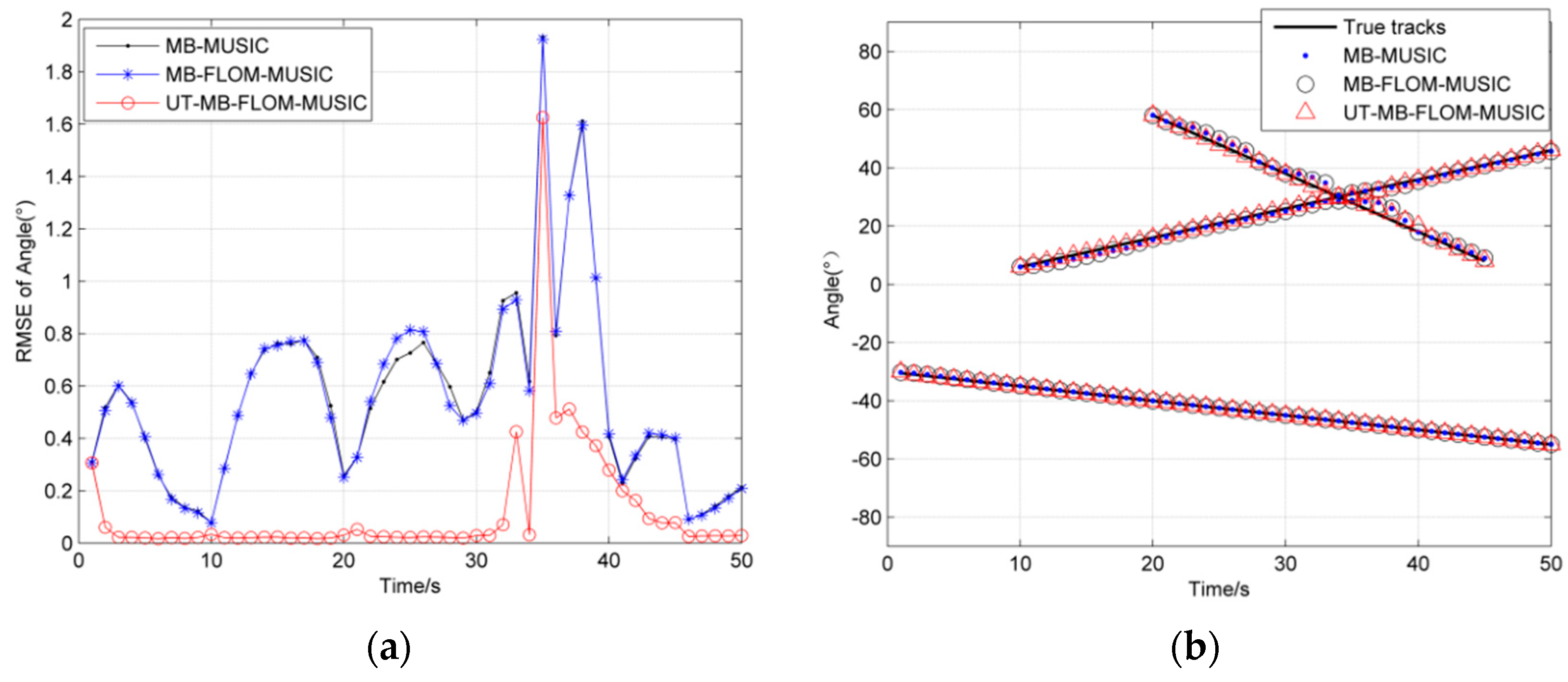

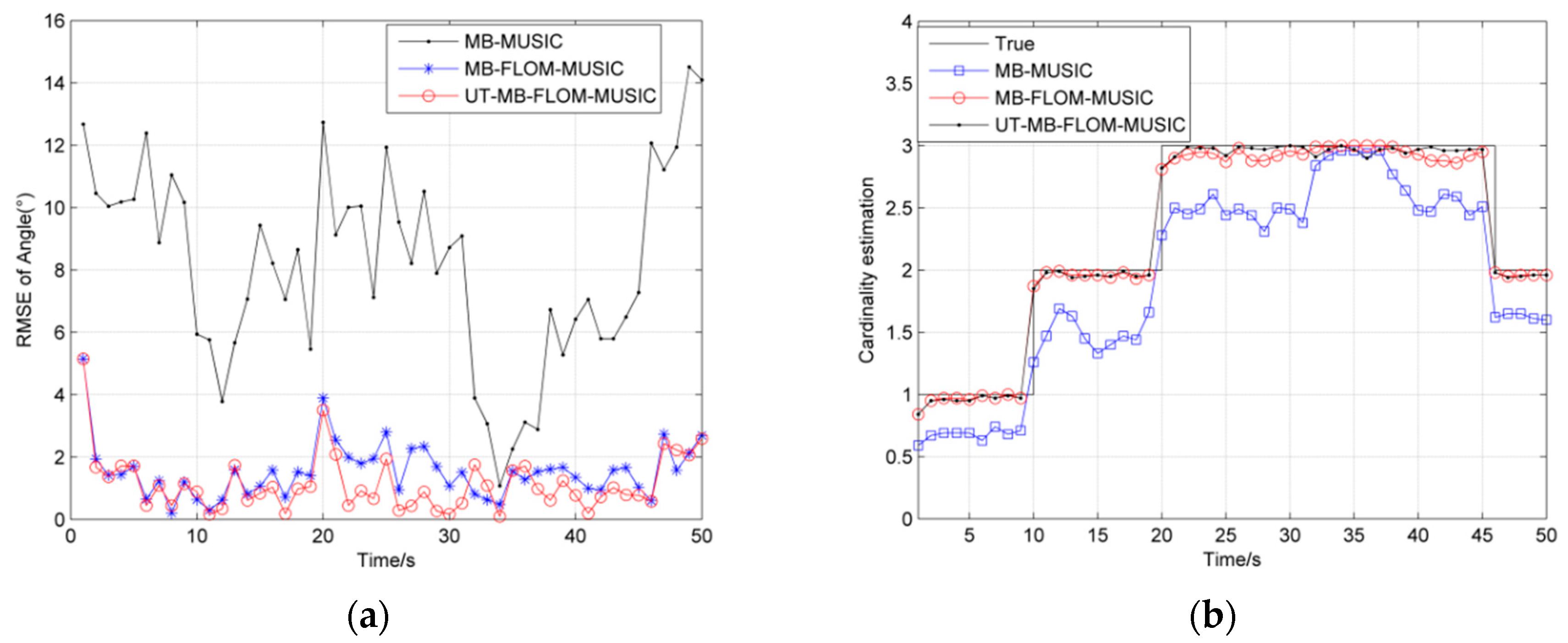
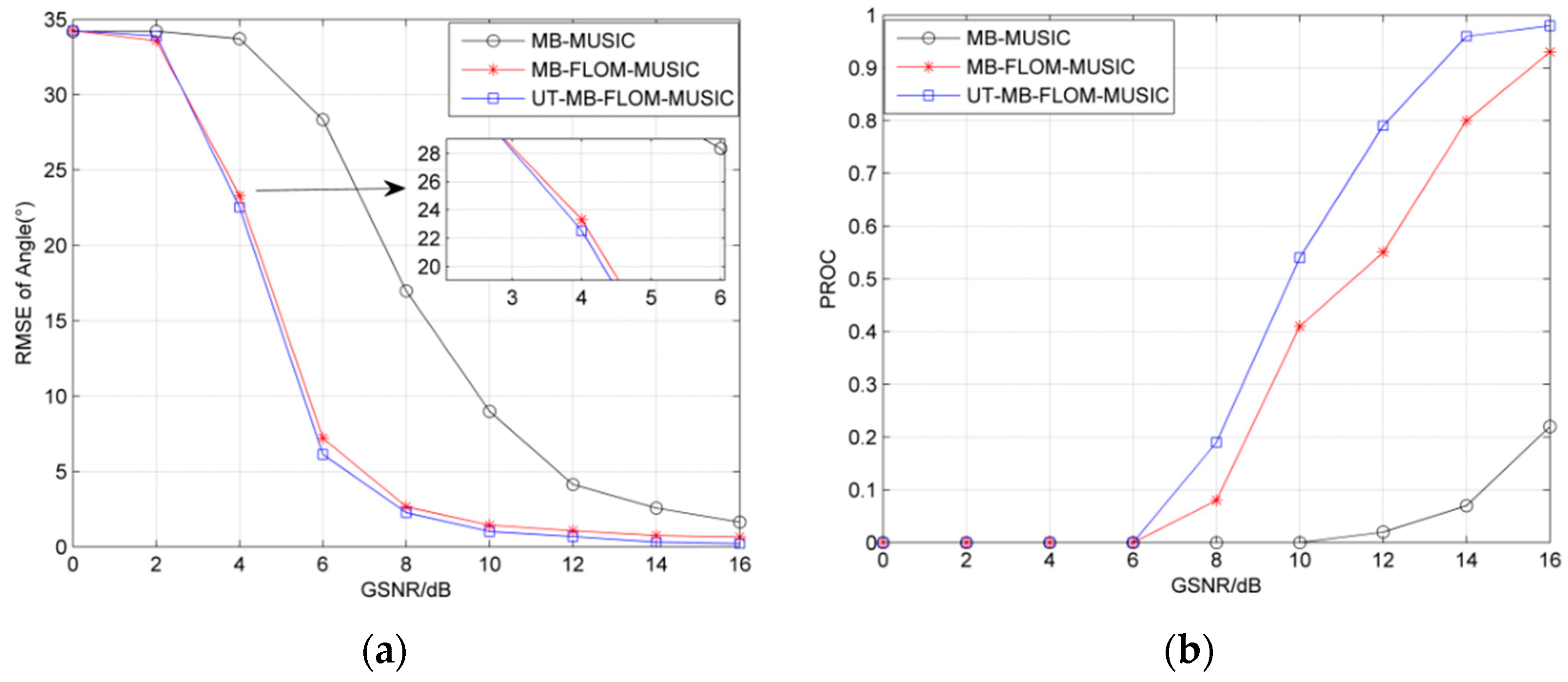
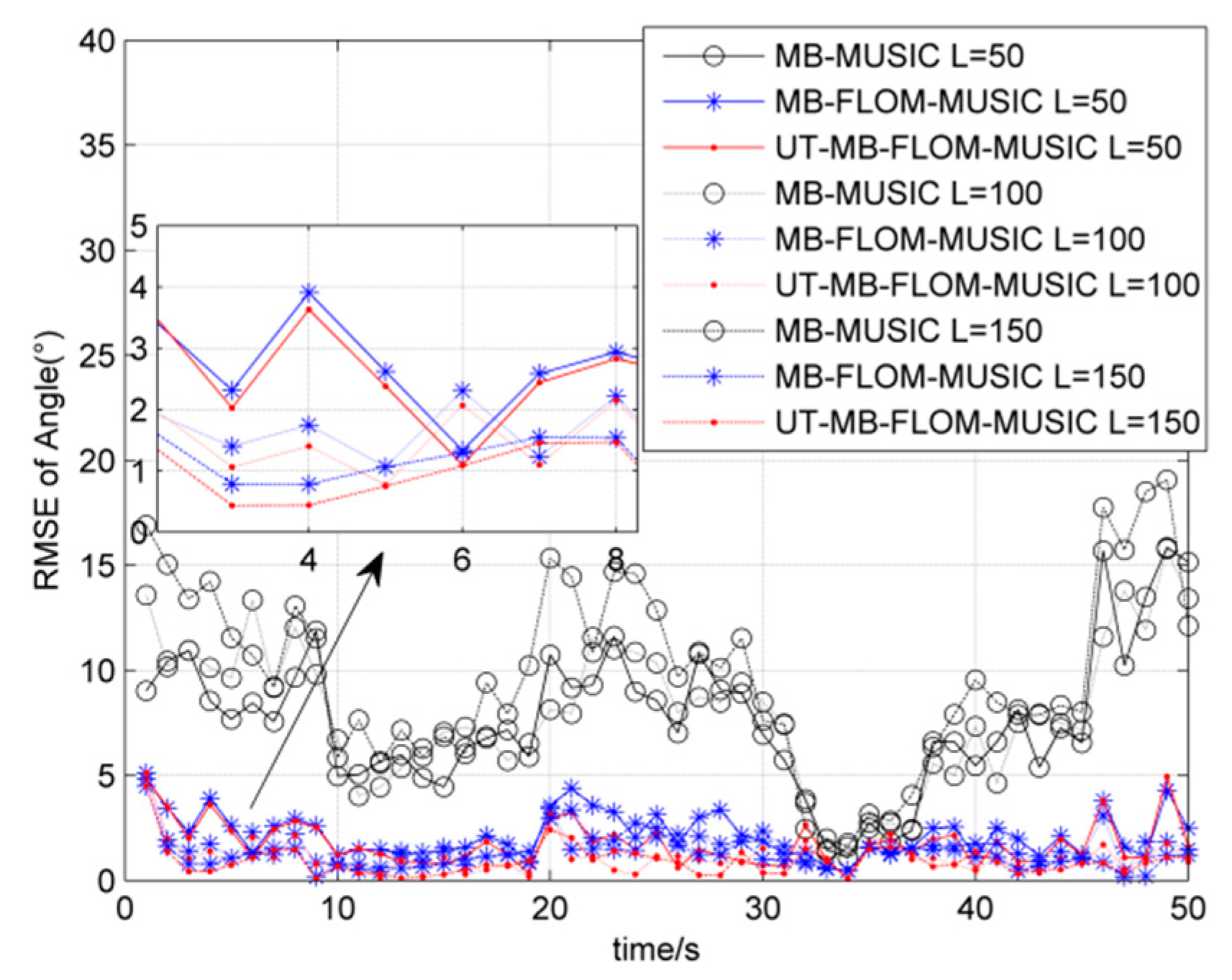

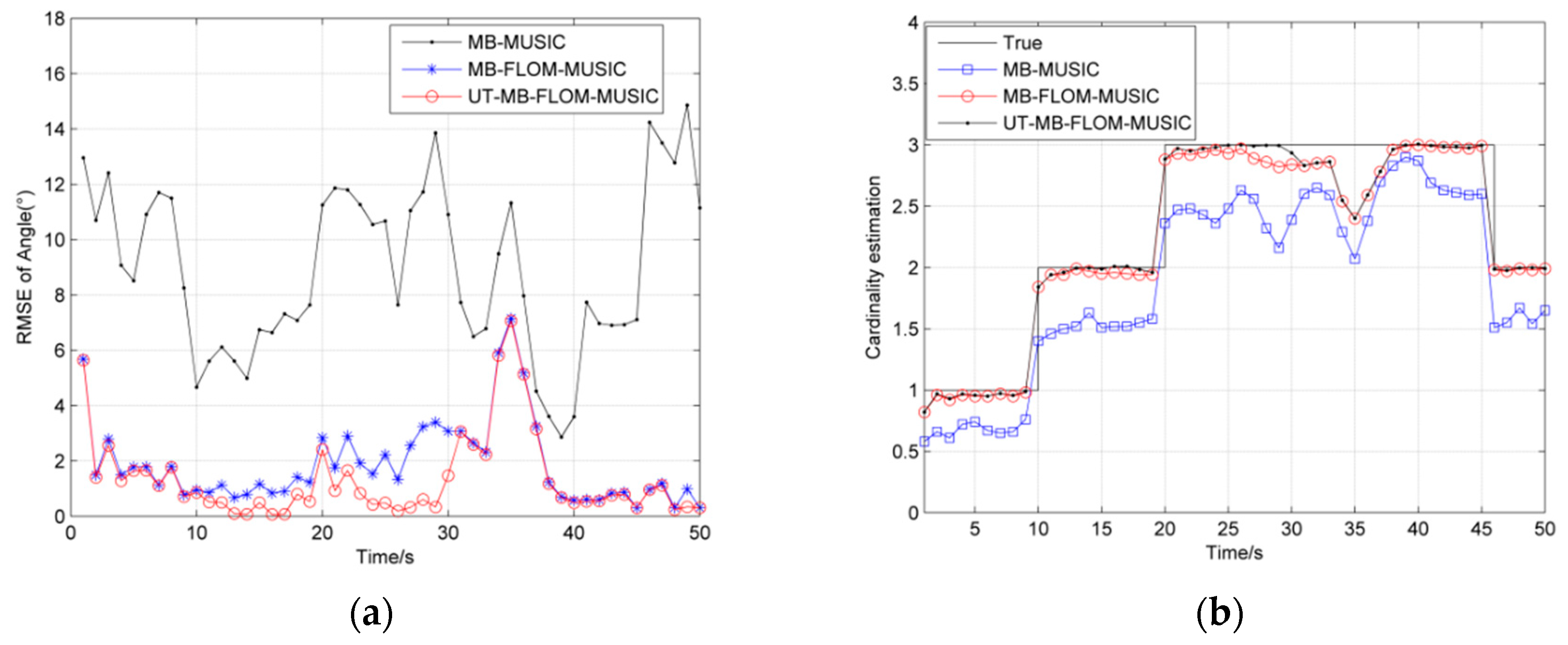
| Algorithm | RMSE | Running Time/s |
|---|---|---|
| MB-MUSIC | 7.6012 | 2.94 |
| MB-FLOM-MUSIC | 1.1396 | 9.59 |
| UT-MB-FLOM-MUSIC | 0.2698 | 114.67 |
| Algorithm | RMSE | Running Time/s |
|---|---|---|
| MB-MUSIC | 8.7728 | 3.67 |
| MB-FLOM-MUSIC | 1.3198 | 10.73 |
| UT-MB-FLOM-MUSIC | 0.6102 | 135.30 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.-y.; Zhao, J.; Dong, X.-d.; Xue, Q.-t.; Cai, R.-h. DOA Tracking Based on Unscented Transform Multi-Bernoulli Filter in Impulse Noise Environment. Sensors 2019, 19, 4031. https://doi.org/10.3390/s19184031
Wu S-y, Zhao J, Dong X-d, Xue Q-t, Cai R-h. DOA Tracking Based on Unscented Transform Multi-Bernoulli Filter in Impulse Noise Environment. Sensors. 2019; 19(18):4031. https://doi.org/10.3390/s19184031
Chicago/Turabian StyleWu, Sun-yong, Jun Zhao, Xu-dong Dong, Qiu-tiao Xue, and Ru-hua Cai. 2019. "DOA Tracking Based on Unscented Transform Multi-Bernoulli Filter in Impulse Noise Environment" Sensors 19, no. 18: 4031. https://doi.org/10.3390/s19184031
APA StyleWu, S.-y., Zhao, J., Dong, X.-d., Xue, Q.-t., & Cai, R.-h. (2019). DOA Tracking Based on Unscented Transform Multi-Bernoulli Filter in Impulse Noise Environment. Sensors, 19(18), 4031. https://doi.org/10.3390/s19184031




