Comparative Study of Coupling Techniques in Lamb Wave Testing of Metallic and Cementitious Plates
Abstract
:1. Introduction
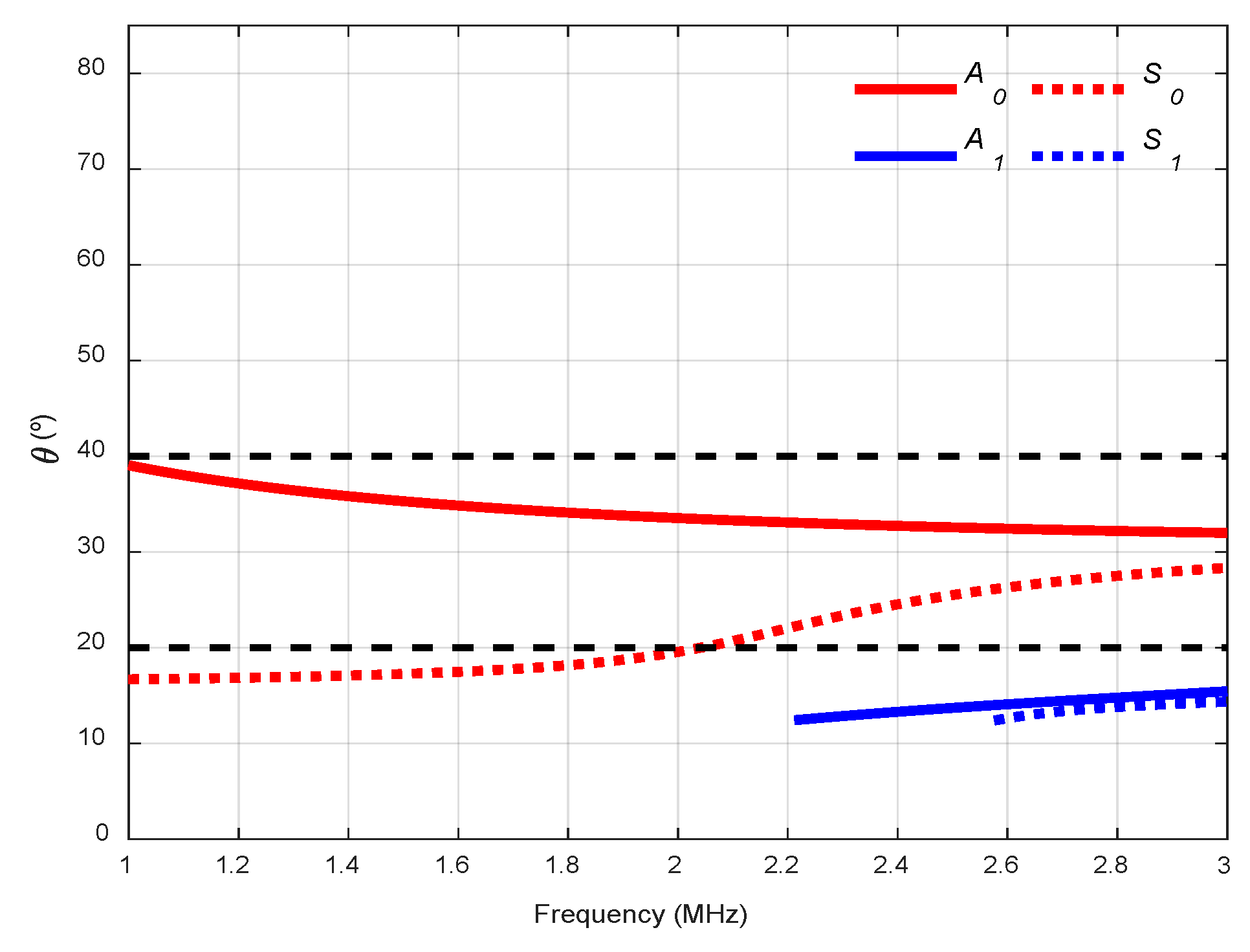
- Low frequencies may be chosen to minimise the number of modes in the received signals, i.e., “working on the left side” of the dispersion curves. In fact, the best would be to excite only one mode because that would enable better damage identification since the appearance of non-excited modes could indicate the existence of defects, i.e., mode conversion [11,15,16].
2. Mathematical Background
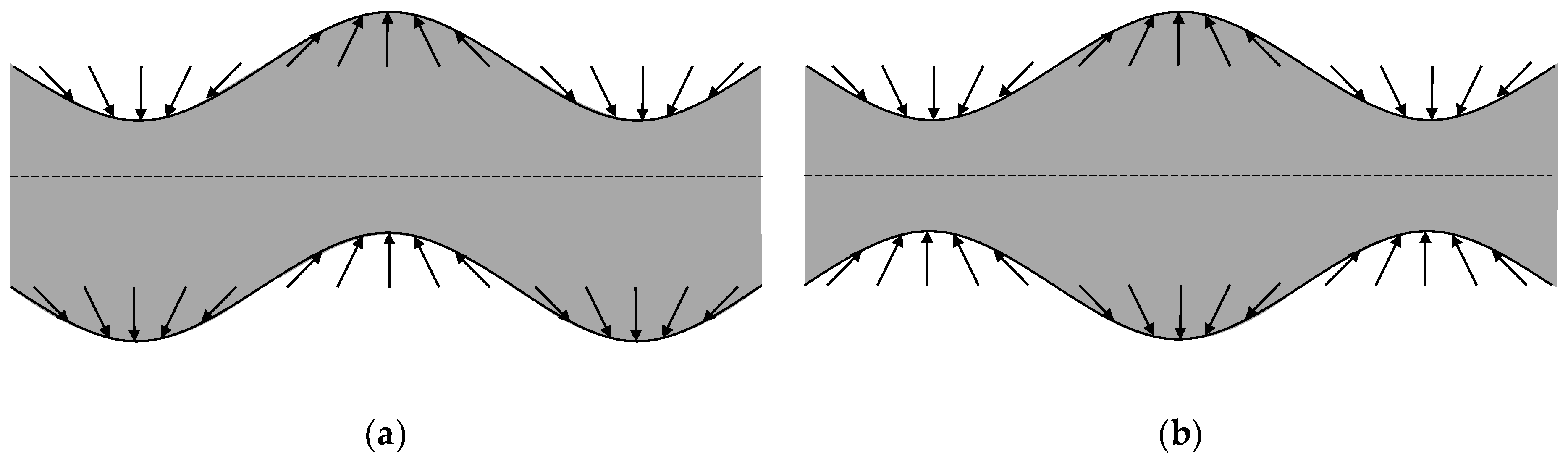
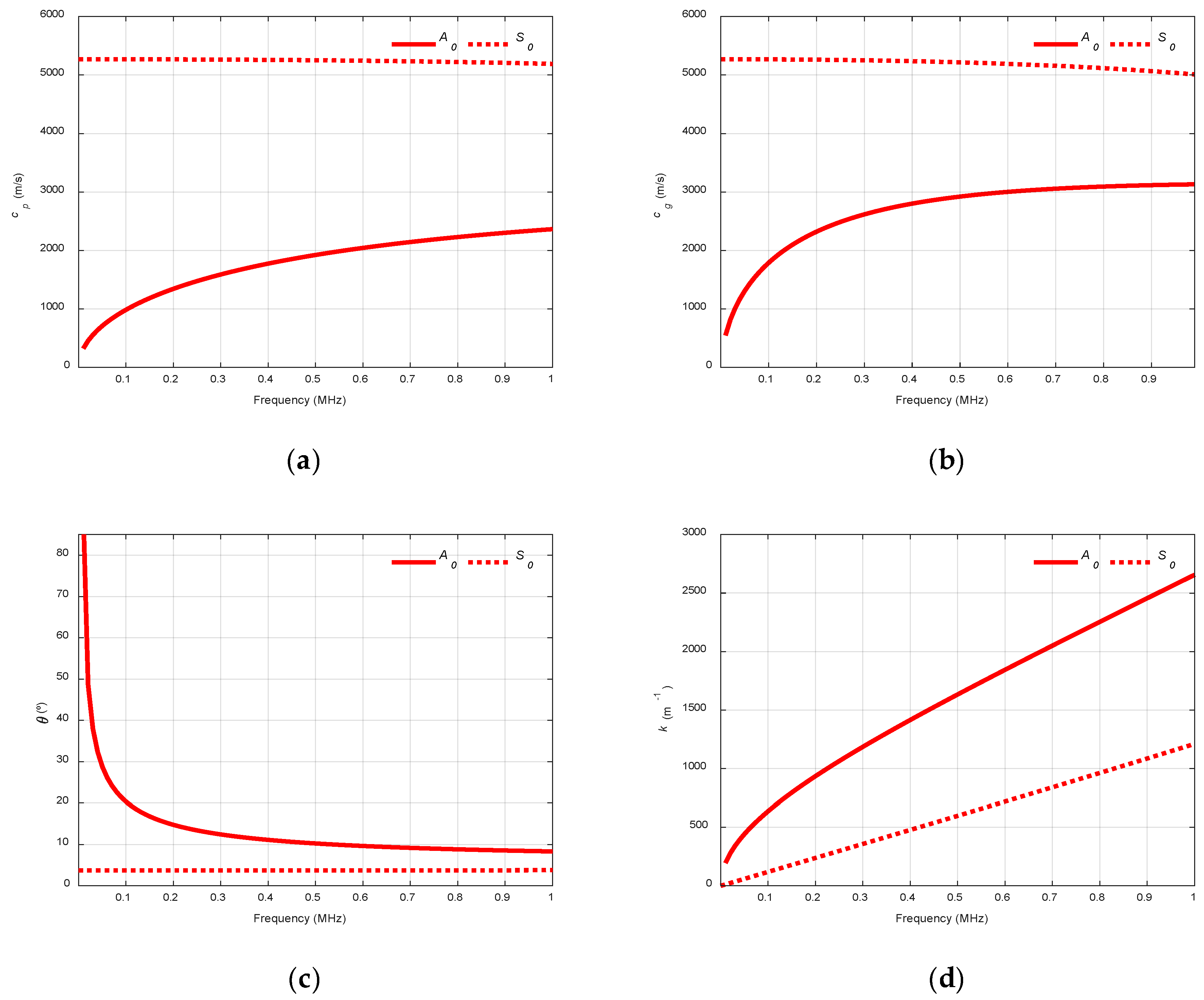
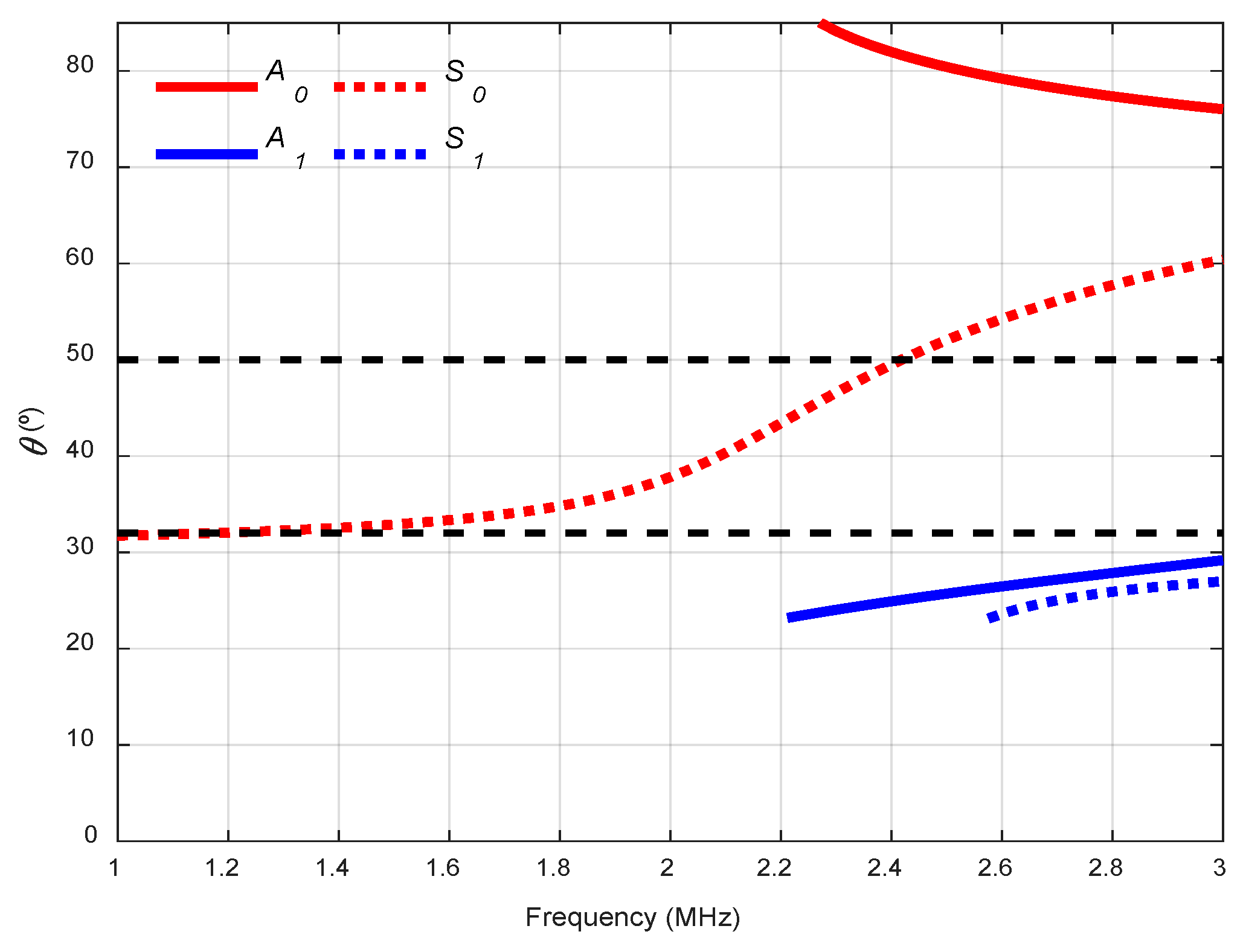
2.1. Theoretical Dispersion Curves
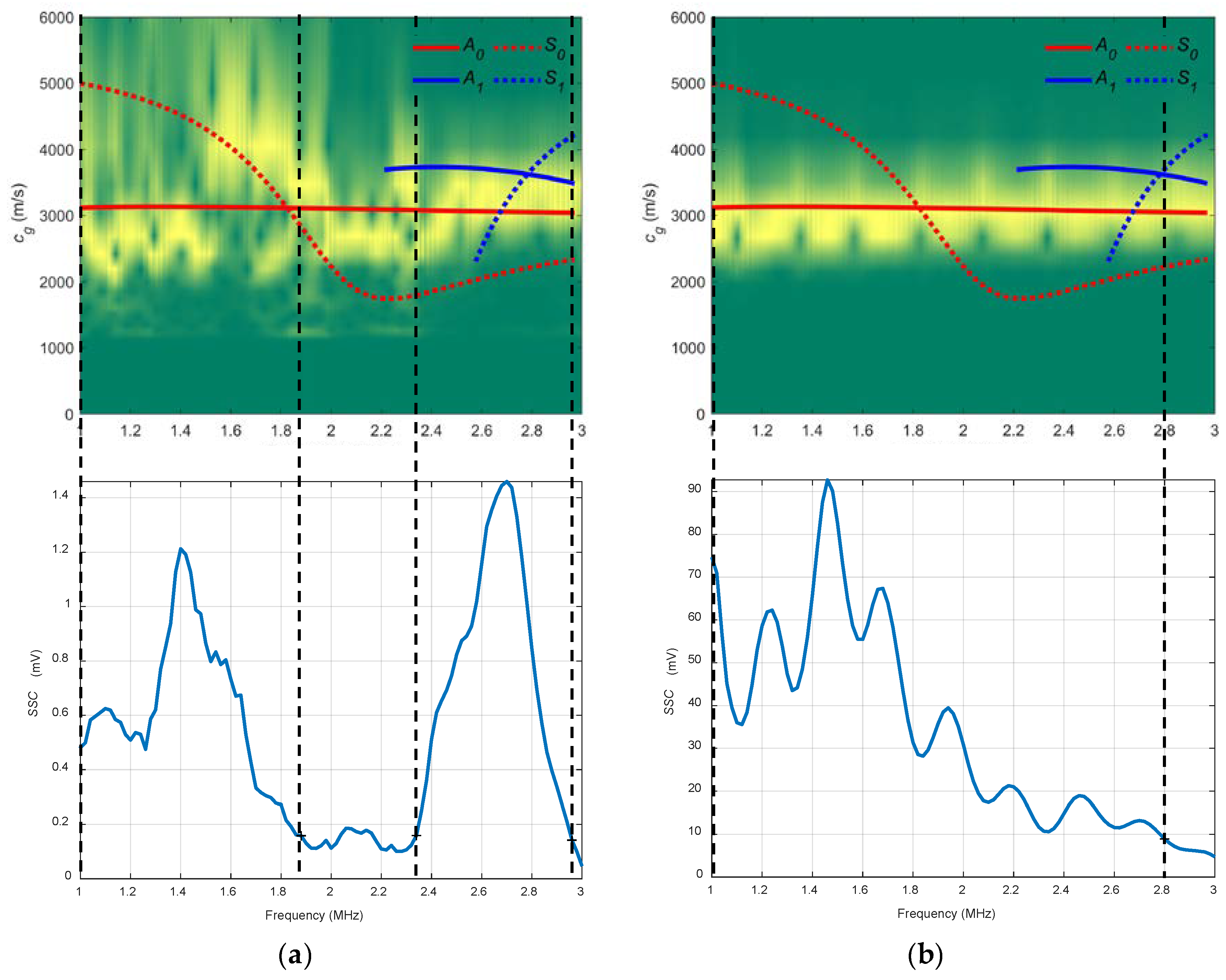
2.2. Experimental Dispersion Curves
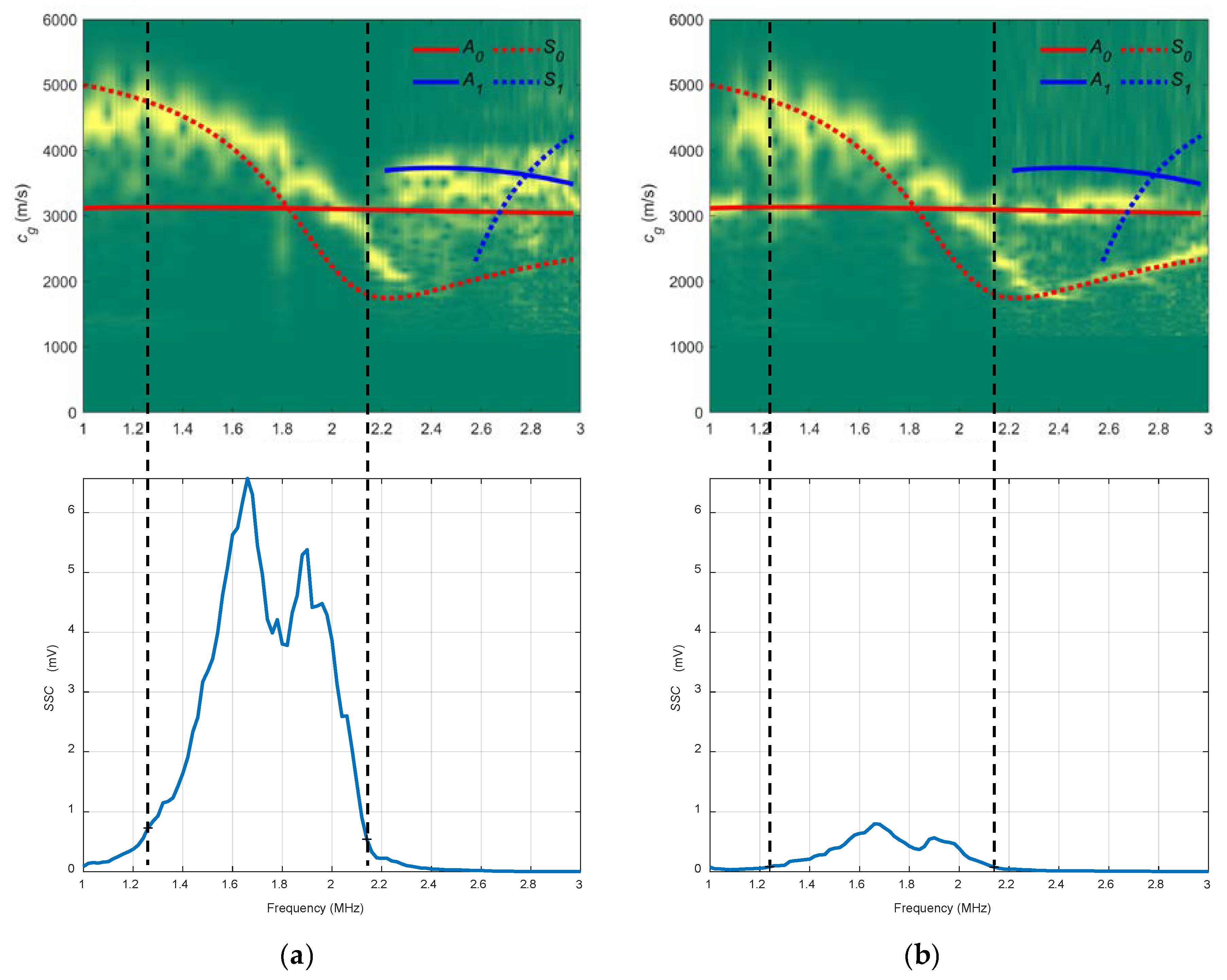
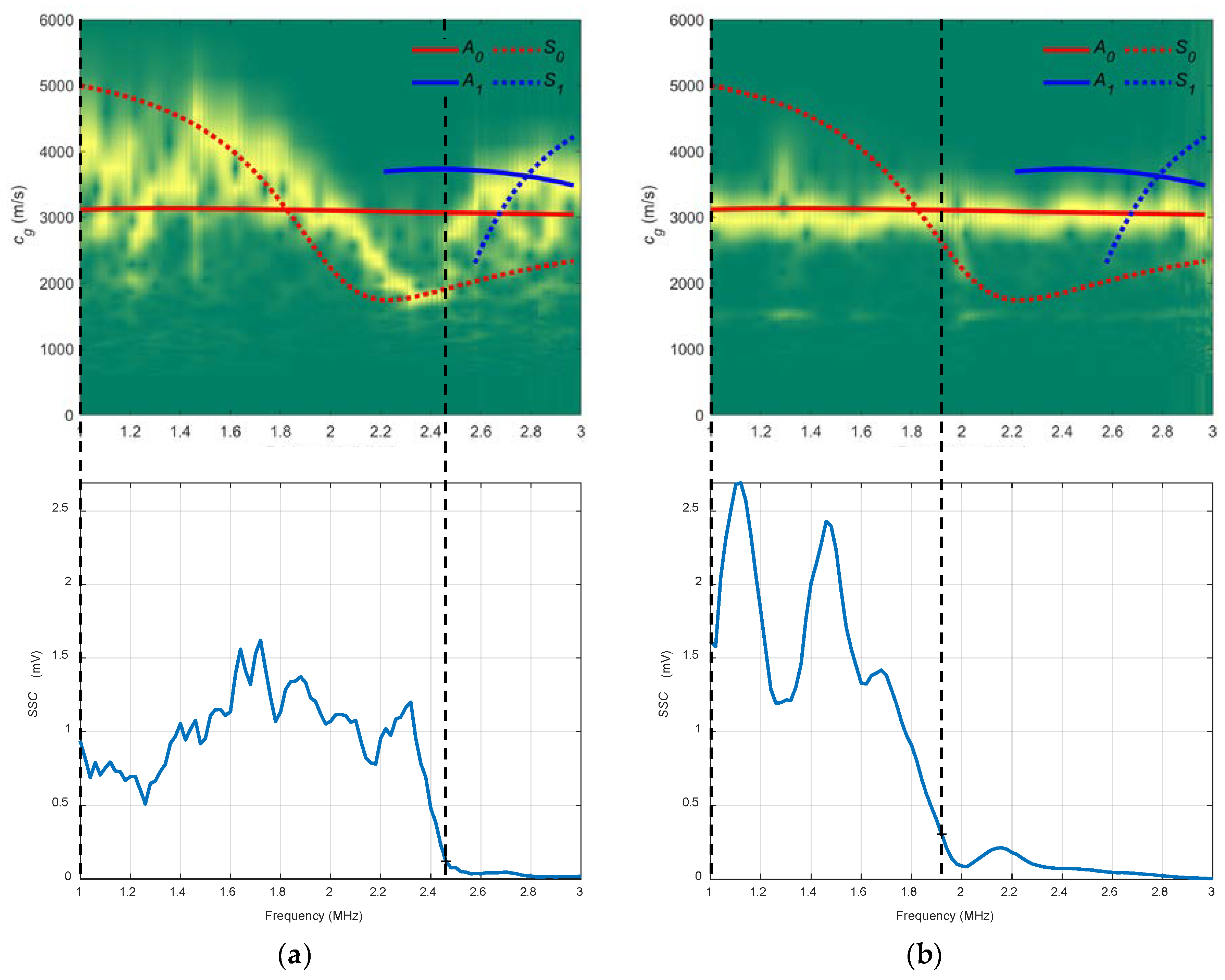
2.3. System Sensitivity Curves
- 1)
- The frequency sweep is performed and tone burst signals of different frequencies (, , …, , where is the number of driving frequencies) are launched on the plate surface by means of the corresponding actuator.
- 2)
- The generated Lamb waves are detected by the sensor and acquired for post-processing.
- 3)
- Signal processing is applied and the spectrograms and the Fourier transforms (FT) for every sensed signal is obtained.
- 4)
- From every spectrogram, a slice including the driving frequency is extracted and then it is normalised by that driving frequency. The slices are represented by rectangles with white discontinuous lines placed on the two spectrograms, and . The combined spectrograms are constructed with slices [37,70].
- 5)
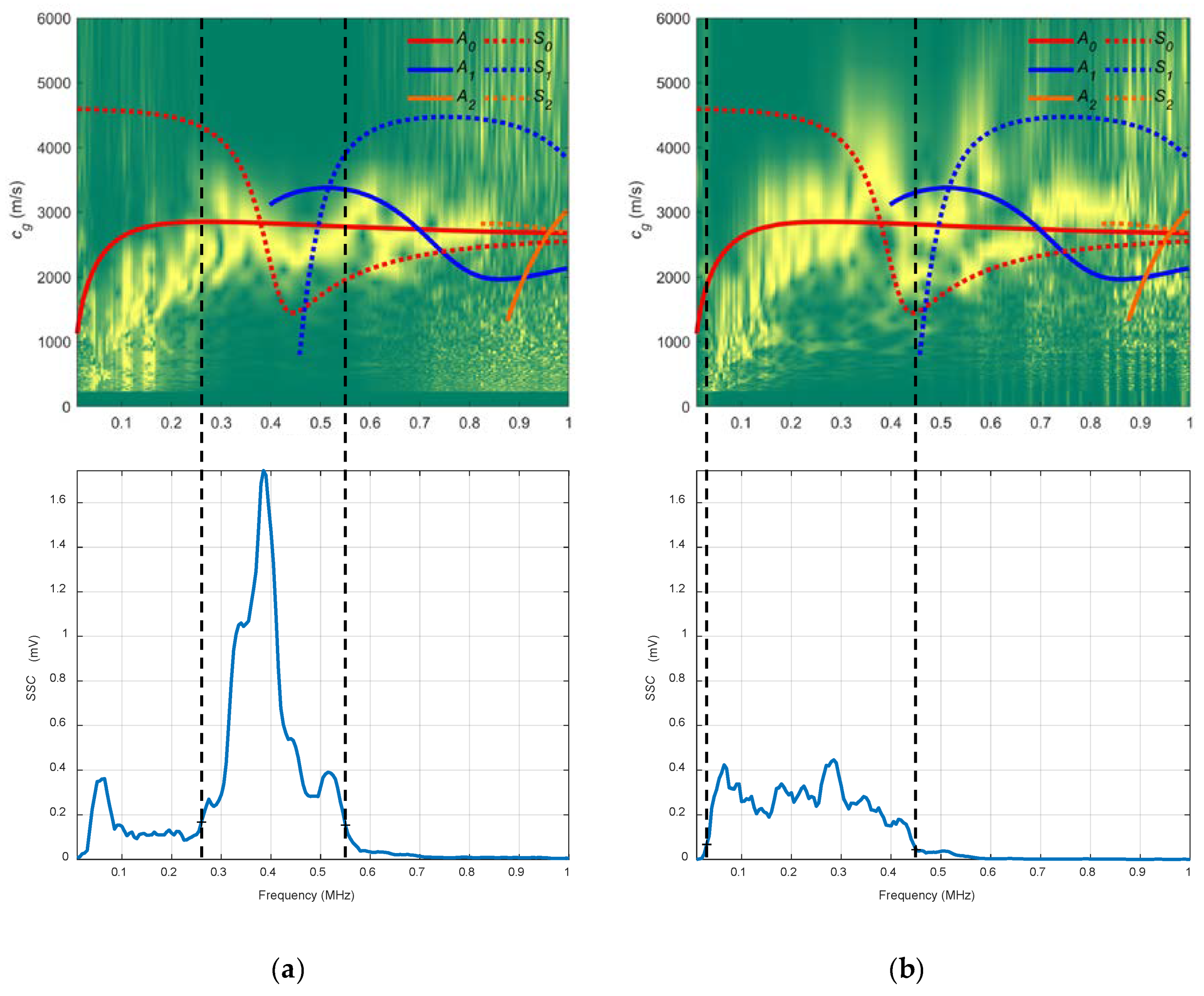
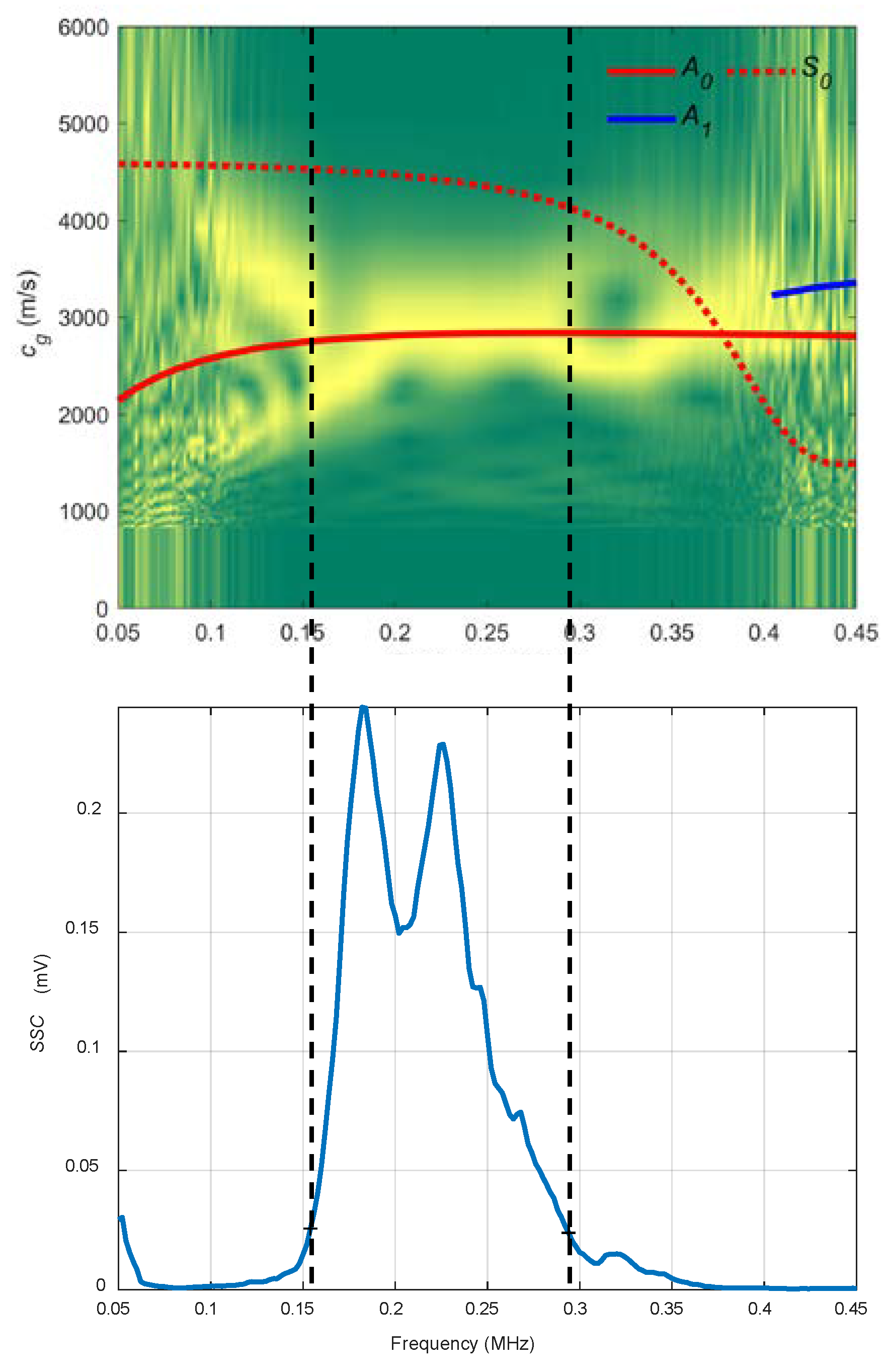
- The SSC are built using the absolute values of the FT of the signals received at every injected frequency: , , …, . These absolute values are marked by blue circles placed on the two FT, and . The maximum in the FT should appear in the excitation frequency, although there are cases where this is not fulfilled. These curves act as a filter to highlight which part of the combined spectrogram can be considered in terms of SNR. In the diagram, the SSC presents more signal level between and . Therefore, the combined spectrogram is analysed in that frequency range, i.e., between the two vertical black discontinuous lines that connects both combined spectrogram and SSC.
3. Experimental
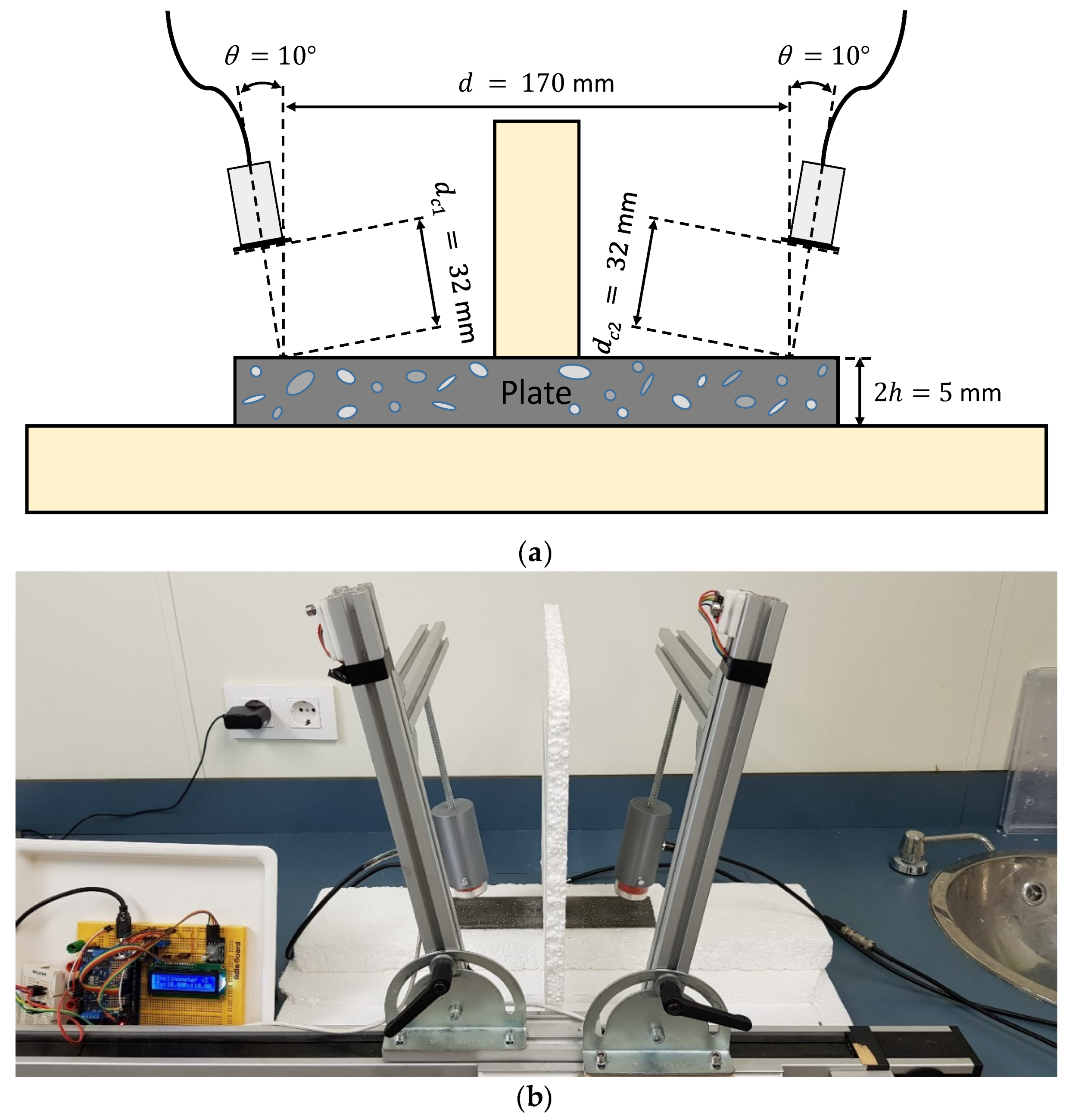
3.1. Materials
3.2. Techniques and Results on Stainless Steel
3.2.1. Direct Contact
3.2.2. Immersion
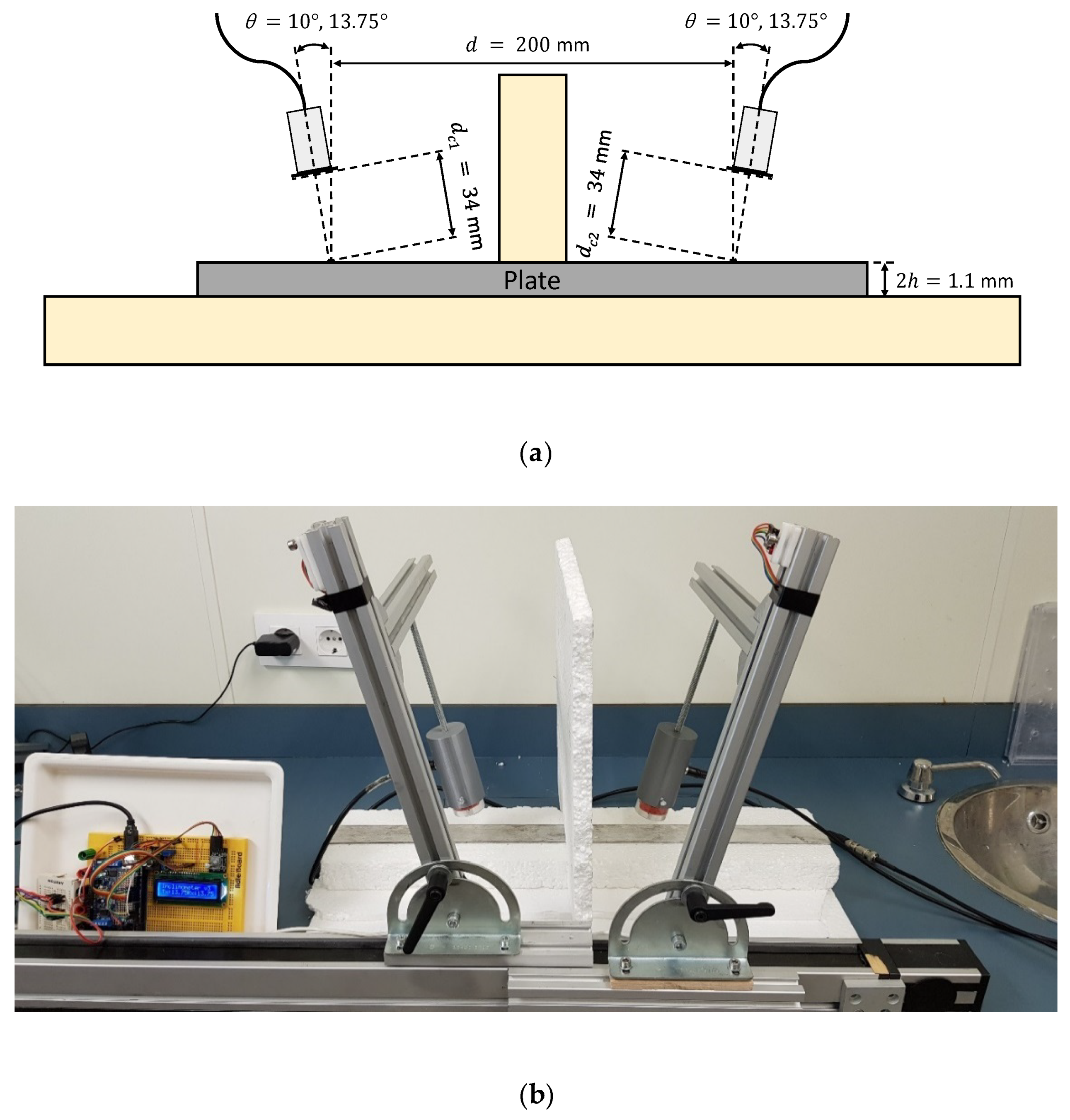
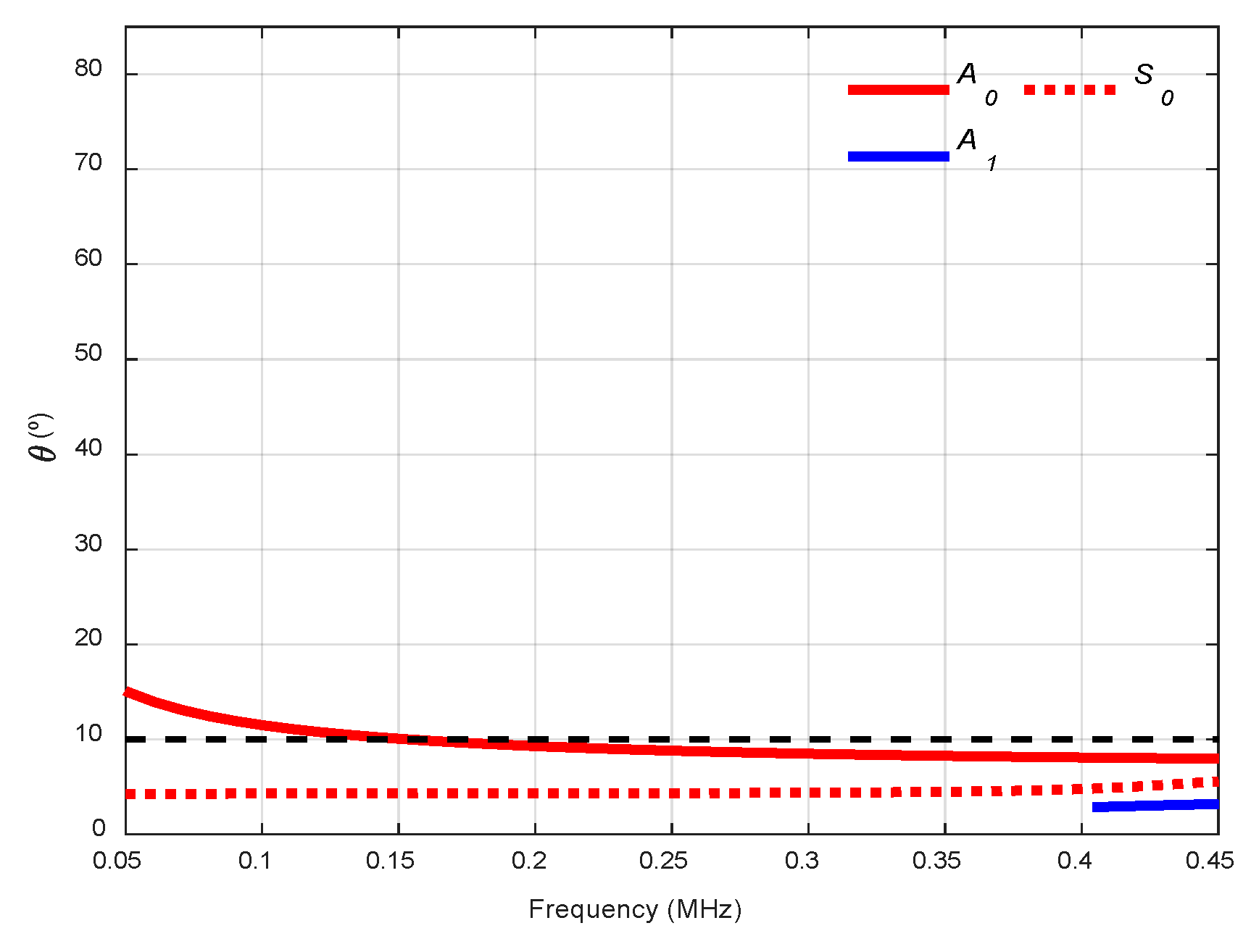
3.2.3. Conical Containers
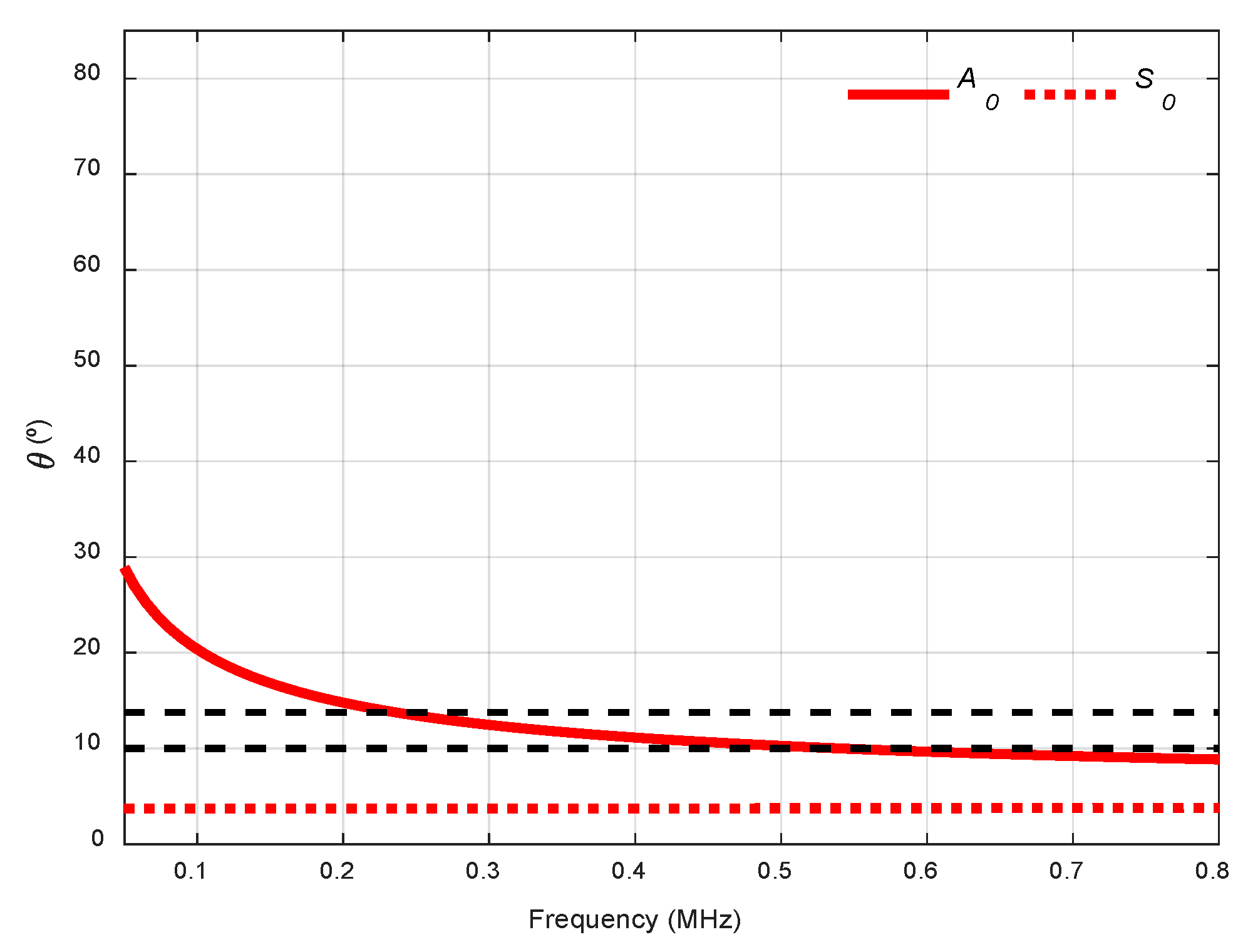
3.2.4. Air Coupling
3.3. Techniques and Results on Mortar
3.3.1. Conical Containers
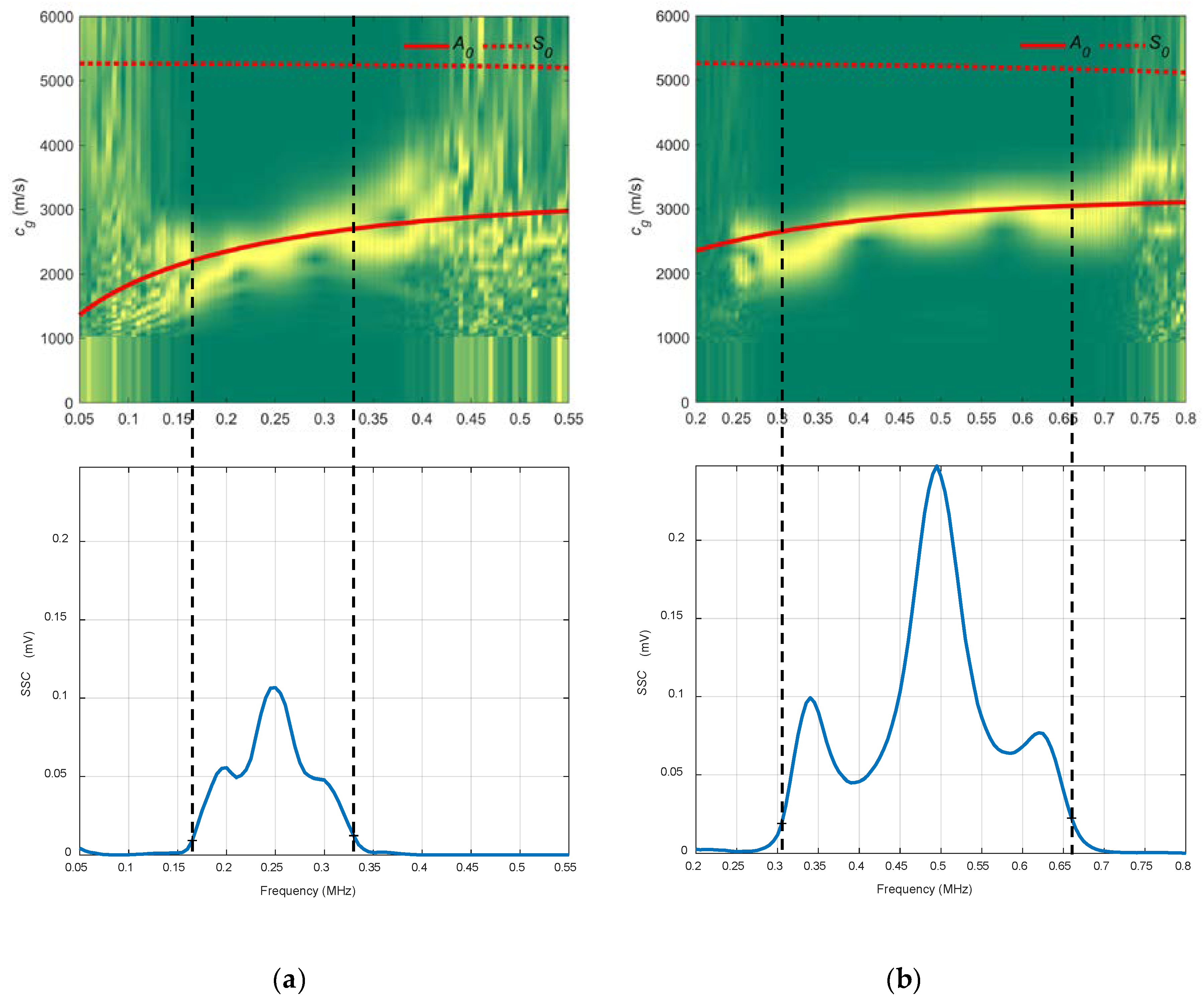
3.3.2. Air Coupling
4. Conclusions
- 1)
- This contribution is a research work where different coupling techniques have been compared and analysed: the contact technique with angle beam probes, pure immersion and alternatives with water wedges, and air-coupled ultrasonic testing. First, a metallic plate was used to perform different experimentals and to achieve a solid theoretical basis. With this theoretical knowledge, a more complicated and heterogeneous material as mortar was inspected.
- 2)
- Good matching between theoretical and experimental group velocity dispersion curves was done to determine which modes were generated in the metallic and mortar plates. Close agreement was achieved between theoretical and experimental data, which means that Lamb waves were excited and received successfully in every setup by choosing the same inclination angle in transmission and reception to enhance a particular Lamb mode.
- 3)
- If the A0 mode is needed, air-coupled ultrasonic testing is recommended as the first option. On the other hand, if S0 mode is sought, water coupling using conical containers is suitable as a first alternative. Plexiglas wedges are also an option to excite the S0 mode if the bulk wave velocities of the tested material are higher than the bulk wave velocity of Plexiglas.
- 4)
- System sensitivity curves (SSC), a signal processing tool that represents the bandwidth of the whole “Lamb wave” system has been of great help to analyse the experimental dispersion curves in the proper frequencies.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Material | Technique | Transducers | Signal Generator | Signal (tone burst) | TX Amplitude (V) | TX Amplification | Frequency Range | Frequency Step (kHz) | Number of Frequencies | RX Amplification (dB) | Acquisition Equipment | Samples | Sampling Frequency (MHz) | Time Interval | Averaging |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stainless steel | Contact | MUBW 2N (2 MHz) | Agilent 33120A | 10 cycle | 10 | x1 | (1 MHz, 3MHz) | 20 | 100 | 40 | DPO3014 | 10000 | 25 | 32 | |
| Immersion | K2SC (2 MHz) | Agilent 33120A | 10 cycle | 10 | x1 | (1 MHz, 3MHz) | 20 | 100 | 40 | DPO3014 | 10000 | 50 | 32 | ||
| Conical containers | K2SC (2 MHz) | Agilent 33120A | 10 cycle | ), ) | x50 | (1 MHz, 3 MHz) | 20 | 100 | 32 | DPO3014 | 10000 | 25 | 32 | ||
| Air coupling | 250 kHz | Agilent 33120A | 5 cycle | 6 | x50 | (50 kHz, 550 kHz) | 5 | 100 | 40 | Rohde & Schwartz RTO 1004 | 10000 | 25 | 32 | ||
| 500 kHz | Agilent 33120A | 5 cycle | 6 | x50 | (200 kHz, 800 kHz) | 5 | 120 | 40 | Rohde & Schwartz RTO 1004 | 10000 | 25 | 32 | |||
| Mortar | Conical containers | K0,5SC (0.5 MHz) | Agilent 33120A | 10 cycle | 3 | No | (10 kHz, 1 MHz) | 5 | 200 | 40 | DPO3014 | 10000 | 10 | 1 ms | 32 |
| Air coupling | 250 kHz | Agilent 33120A | 5 cycle | 6 | x50 | (50 kHz, 450 kHz) | 2 | 200 | 40 | Rohde & Schwartz RTO 1004 | 10000 | 10 | 1 ms | 32 |
References
- Rose, J.L. Ultrasonic Guided Waves in Solid Media, 1st ed.; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Rossing, T.D.; Fletcher, N.H. Principles of Vibration and Sound, 2nd ed.; Springer-Verlag: New York, NY, USA, 2004. [Google Scholar]
- Sharma, S.; Mukherjee, A. Damage detection in submerged plates using ultrasonic guided waves. Sadhana 2014, 39, 1009–1034. [Google Scholar] [CrossRef]
- Luo, W.; Rose, J.L. Lamb Wave Thickness Measurement Potential with Angle Beam and Normal Beam Excitation. Mater. Eval. 2004, 62, 860–866. [Google Scholar]
- Yung, Y.C.; Kundu, T.; Ehsani, M.R. Internal Discontinuity Detection in Concrete by Lamb Waves. Mater. Eval. 2001, 59, 418–423. [Google Scholar]
- Su, Z.; Ye, L. Identification of Damage Using Lamb Waves: From Fundamentals to Applications, 1st ed.; Springer-Verlag: London, UK, 2009. [Google Scholar]
- Birgani, P.T.; Tahan, K.N.; Sodagar, S.; Shishesaz, M. Theoretical modeling of low-attenuation lamb wave modes generation in three-layer adhesive joints using angle beam transducer. Lat. Am. J. Solids Stru. 2015, 12, 461–476. [Google Scholar] [CrossRef] [Green Version]
- Gómez Ullate, Y.; Reynolds, P.; Mould, J. Selective excitation of Lamb Wave Modes in Thin Aluminium Plates using Bonded Piezoceramics: FEM Modelling and Measurements. In Proceedings of the 9th European Conference on NDT, Berlin, Germany, 25–29 September 2006. [Google Scholar]
- Seale, M.D.; Smith, B.T.; Prosser, W.H. Lamb wave assessment of fatigue and thermal damage in composites. J. Acoust. Soc. Am. 1998, 103, 2416–2424. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Lamb Wave Generation with Piezoelectric Wafer Active Sensors for Structural Health Monitoring. In Proceedings of the SPIE’s 10th Annual International Symposium on Smart Structures and Materials, San Diego, CA, USA, 2–6 March 2002. [Google Scholar]
- Alleyne, D.N.; Cawley, P. Optimization of Lamb wave inspection techniques. NDT E Int. 1992, 25, 11–22. [Google Scholar] [CrossRef]
- Cawley, P.; Alleyne, D. The use of Lamb waves for the long range inspection of large structures. Ultrasonics 1996, 34, 287–290. [Google Scholar] [CrossRef]
- Sharma, S.; Mukherjee, A. A Non-Contact Technique for Damage Monitoring in Submerged Plates Using Guided Waves. J. Test. Eval. 2015, 43, 776–791. [Google Scholar] [CrossRef]
- Jia, X. Modal analysis of Lamb wave generation in elastic plates by liquid wedge transducers. J. Acoust. Soc. Am. 1997, 101, 834–842. [Google Scholar] [CrossRef]
- Pitch-Catch Air-Coupled Ultrasonic Technique for Detection of Barely Visible Impact Damages in Composite Laminates. In Proceedings of the 7th European Workshop on Structural Health Monitoring, Nantes, France, 8–11 July 2014.
- Shelke, A.; Kundu, T.; Amjad, U.; Hahn, K.; Grill, W. Mode-Selective Excitation and Detection of Ultrasonic Guided Waves for Delamination Detection in Laminated Aluminum Plates. IEEE T. Ultrason. Ferr. 2011, 58, 567–577. [Google Scholar] [CrossRef]
- Chen, J.; Su, Z.; Cheng, L. Identification of corrosion damage in submerged structures using fundamental anti-symmetric Lamb waves. Smart Mater. Struct. 2010, 19, 015004. [Google Scholar] [CrossRef]
- Masurkar, F.A.; Yelve, N.P. Locating a Damage in an Aluminium Plate using Lamb Waves. In Proceedings of the Indian National Seminar & Exhibition on Non-Destructive Evaluation, Hyderabad, India, 26–28 November 2015. [Google Scholar]
- Ham, S.; Popovics, J.S. Fast Lamb Wave Energy Shift Approach Using Fully Contactless Ultrasonic System to Characterize Concrete Structures. In Proceedings of the 41st Annual Review of Progress in Quantitative Nondestructive Evaluation, Boise, ID, USA, 20–25 July 2015. [Google Scholar]
- Rajana, K.M.; Cho, Y.; Rose, J.L. Utility of Lamb Waves for Near Surface Crack Detection. In Review of Progress in Quantitative Nondestructive Evaluation; Thompson, D.O., Chimenti, D.E., Eds.; Springer: Boston, MA, USA, 1996; pp. 247–252. [Google Scholar] [Green Version]
- Benz, R.; Niethammer, M.; Hurlebaus, S.; Jacobs, L.J. Localization of notches with Lamb waves. J. Acoust. Soc. Am. 2003, 114, 677–685. [Google Scholar] [CrossRef] [PubMed]
- Beadle, B.M.; Hurlebaus, S.; Jacobs, L.J.; Gaul, L. Detection and Localization of Small Notches in Plates Using Lamb Waves. In Proceedings of the 23rd Conference and Exposition on Structural Dynamics (IMAC–XXIII), Orlando, FL, USA, 31 January–3 February 2005. [Google Scholar]
- Singh, R.; Sharma, D.S.; Sharma, M.S. Guided Waves for Damage Monitoring in Plates with Corrosion Defects. Int. J. Innov. Res. Sci. Eng. Technol. 2014, 3, 10072–10083. [Google Scholar]
- Guo, N.; Cawley, P. The interaction of Lamb waves with delaminations in composite laminates. J. Acoust. Soc. Am. 1993, 94, 2240–2246. [Google Scholar] [CrossRef]
- Xu, K.; Ta, D.; Moilanen, P.; Wang, W. Mode separation of Lamb waves based on dispersion compensation method. J. Acoust. Soc. Am. 2012, 131, 2714–2722. [Google Scholar] [CrossRef]
- Viktorov, I.A. Rayleigh and Lamb Waves: Physical Theory and Applications, 1st ed.; Springer: Boston, MA, USA, 1967. [Google Scholar]
- Guo, D.; Kundu, T. A new transducer holder mechanism for pipe inspection. J. Acoust. Soc. Am. 2001, 110, 303–309. [Google Scholar] [CrossRef]
- Ghosh, T.; Kundu, T.; Karpur, P. Efficient use of Lamb modes for detecting defects in large plates. Ultrasonics 1998, 36, 791–801. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Cuc, A. Embedded Non-destructive Evaluation for Structural Health Monitoring, Damage Detection, and Failure Prevention. Shock Vib. Dig. 2005, 37, 83–105. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Tuned Lamb Wave Excitation and Detection with Piezoelectric Wafer Active Sensors for Structural Health Monitoring. J. Intell. Mater. Syst. Struct. 2005, 16, 291–305. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors, 2nd ed.; Academic Press: Waltham, MA, USA, 2014. [Google Scholar]
- Rguiti, M.; Grondel, S.; El youbi, F.; Courtois, C.; Lippert, M.; Leriche, A. Optimized piezoelectric sensor for a specific application: Detection of Lamb waves. Sens. Actuators A Phys. 2006, 126, 362–368. [Google Scholar] [CrossRef]
- Kessler, S.S.; Spearing, S.M.; Soutis, C. Damage detection in composite materials using Lamb wave methods. Smart Mater. Struct. 2002, 11, 269–278. [Google Scholar] [CrossRef] [Green Version]
- Mustapha, S.; Ye, L. Bonding Piezoelectric Wafers for Application in Structural Health Monitoring–Adhesive Selection. Res. Nondestruct. Eval. 2015, 26, 23–42. [Google Scholar] [CrossRef]
- Sun, H.; Wang, Y.; Qing, X.; Wu, Z. High Strain Survivability of Piezoceramics by Optimal Bonding Adhesive Design. Sensors 2018, 18, 2554. [Google Scholar] [CrossRef] [PubMed]
- Alleyne, D.; Cawley, P. A two-dimensional Fourier transform method for the measurement of propagating multimode signals. J. Acoust. Soc. Am. 1991, 89, 1159–1168. [Google Scholar] [CrossRef]
- Bezdek, M.; Joseph, K.; Tittmann, B.R. Low Attenuation Waveguide for Structural Health Monitoring with Leaky Surface Waves. J. Korean Soc. Nondestruct. Test. 2012, 32, 241–262. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.H.; Song, S.-J.; Kwon, S.-D. Measurement of phase velocity dispersion curves and group velocities in a plate using leaky Lamb waves. In Proceedings of the National Seminar of ISNT, Chennai, Tamil Nadu, India, 5–7 December 2002. [Google Scholar]
- Harb, M.S.; Yuan, F.G. A rapid, fully non-contact, hybrid system for generating Lamb wave dispersion curves. Ultrasonics 2015, 61, 62–70. [Google Scholar] [CrossRef] [PubMed]
- Castaings, M.; Cawley, P. The generation, propagation, and detection of Lamb waves in plates using air-coupled ultrasonic transducers. J. Acoust. Soc. Am. 1996, 100, 3070–3077. [Google Scholar] [CrossRef]
- Theobald, P.; Zeqiri, B.; Avison, J. Couplants and their Influence on AE sensor sensitivity. J. Acoust. Emiss. 2008, 26, 91–97. [Google Scholar]
- Alleyne, D.N.; Cawley, P. The Interaction of Lamb Waves with Defects. IEEE Trans. Ultrason. Ferroelectr. 1992, 39, 381–397. [Google Scholar] [CrossRef]
- Mažeika, L.; Raišutis, R.; Maciulevičius, A.; Žukauskas, E.; Kazys, R.; Seniūnas, G.; Vladišauskas, A. Comparison of several techniques of ultrasonic Lamb waves velocities measurements. Ultragarsas (Ultrasound) 2009, 64, 11–17. [Google Scholar]
- Lee, K.I.; Yoon, S.W. Feasibility of bone assessment with leaky Lamb waves in bone phantoms and a bovine tibia. J. Acoust. Soc. Am. 2004, 115, 3210–3217. [Google Scholar] [CrossRef] [PubMed]
- Alleyne, D.N. The nondestructive testing of plates using ultrasonic Lamb waves. PhD Thesis, Imperial College of Science, Technology and Medicine - University of London, London, UK, 1991. [Google Scholar]
- Lee, Y.C.; Cheng, S.W. Measuring Lamb Wave Dispersion Curves of a Bi-Layered Plate and Its Application on Material Characterization of Coating. IEEE Trans. Ultrason. Ferroelectr. 2001, 48, 830–837. [Google Scholar]
- Takiy, A.E.; Granja, S.C.G.; Higuti, R.T.; Kitano, C.; Elvira, L.; Martínez-Graullera, O.F. Low attenuation frequency bands for Lamb waves immersed in viscous fluids: theoretical analysis and experimental validation. In Proceedings of the International Congress on Ultrasonics (ICU), Singapore, 2–5 May 2013. [Google Scholar]
- Karpur, P.; Benson, D.M.; Matikas, T.E.; Kundu, T.; Nicolaou, P.D. An Approach to Determine the Experimental Transmitter-Receiver Geometry for the Reception of Leaky Lamb Waves. Mater. Eval. 1995, 53, 1348–1352. [Google Scholar]
- Goueygou, M.; Abraham, O.; Lataste, J.-F. A comparative study of two non-destructive testing methods to assess near-surface mechanical damage in concrete structures. NDT E Int. 2008, 41, 448–456. [Google Scholar] [CrossRef]
- Briers, R.; Leroy, O.; Shkerdin, G. A liquid wedge as generating technique for Lamb and Rayleigh waves. J. Acoust. Soc. Am. 1997, 102, 2117–2124. [Google Scholar] [CrossRef]
- Padiyar, M.J.; Hariharan, N.; Maheswaran, M.; Balasubramaniam, K.; Bose, A.C.; Giridharan, N.V. Increase in efficiency of air-coupled L-scan (Lamb wave scan) and its application in inspection of composite structures. In Proceedings of the National Seminar & Exhibition on Non-Destructive Evaluation, Chennai, India, 8–10 December 2011. [Google Scholar]
- Hayashi, T.; Kawashima, K. Single Mode Extraction from Multiple Modes of Lamb Wave and Its Application to Defect Detection. JSME Int. J. Ser. A 2003, 46, 620–626. [Google Scholar] [CrossRef] [Green Version]
- Gosálbez, J.; Wright, W.M.D.; Jiang, W.; Carrión, A.; Genovés, V.; Bosch, I. Airborne non-contact and contact broadband ultrasounds for frequency attenuation profile estimation of cementitious materials. Ultrasonics 2018, 88, 148–156. [Google Scholar] [CrossRef]
- Solodov, I.; Döring, D.; Busse, G. Air-Coupled Lamb and Rayleigh Waves for Remote NDE of Defects and Material Elastic Properties. J. Mech. Eng. 2010, 56, 557–564. [Google Scholar]
- Schindel, D.W.; Hutchins, D.A.; Grandia, W.A. Capacitive and piezoelectric air-coupled transducers for resonant ultrasonic inspection. Ultrasonics 1996, 34, 621–627. [Google Scholar] [CrossRef]
- Schindel, D.W.; Hutchins, D.A. Through-thickness characterization of solids by wideband air-coupled ultrasound. Ultrasonics 1995, 33, 11–17. [Google Scholar] [CrossRef]
- In, C.-W.; Kim, J.-Y.; Kurtis, K.E.; Jacobs, L.J. Characterization of ultrasonic Rayleigh surface waves in asphaltic concrete. NDT E Int. 2009, 42, 610–617. [Google Scholar] [CrossRef]
- Fan, Z.; Jiang, W.; Wright, W.M.D. Non-contact ultrasonic gas flow metering using air-coupled leaky Lamb waves. Ultrasonics 2018, 89, 74–83. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.; Jiang, W.; Cai, M.; Wright, W.M.D. The effects of air gap reflections during air-coupled leaky Lamb wave inspection of thin plates. Ultrasonics 2016, 65, 282–295. [Google Scholar] [CrossRef] [PubMed]
- Demčenko, A.; Žukauskas, A.D.E.; Kazys, R.; Voleisis, A. Investigation of interaction of the Lamb wave with delamination type defect in GLARE composite using air-coupled ultrasonic technique. In Proceedings of the Forum Acusticum Budapest: 4th European Congress on Acoustics, Budapest, Hungary, 29 August–2 September 2005. [Google Scholar]
- Zhao, M.; Zeng, L.; Lin, J.; Wu, W. Mode identification and extraction of broadband ultrasonic guided waves. Meas. Sci. Technol. 2014, 25, 115005. [Google Scholar] [CrossRef]
- Ryden, N.; Park, C.B.; Ulriksen, P.; Miller, R.D. Lamb wave analysis for non-destructive testing of concrete plate structures. In Proceedings of the 9th European Meeting of Environmental and Engineering Geophysics (EEGS-ES / EAGE Near Surface Geoscience Division annual meeting), Prague, Czech Republic, 31 August–4 September 2003; pp. 782–793. [Google Scholar]
- Lee, Y.H.; Oh, T. The Simple Lamb Wave Analysis to Characterize Concrete Wide Beams by the Practical MASW Test. Materials 2016, 9, 437. [Google Scholar] [CrossRef] [PubMed]
- Karpenko, O. Signal Analysis in Guided Wave Structural Health Monitoring. Master’s Thesis, Michigan State University, East Lansing, MI, USA, 2013. [Google Scholar]
- Moll, J.; Fritzen, C.-P. Advanced Aspects of Mode-Selective Excitation of Ultrasonic Guided Waves. In Proceedings of the ISMA 2010: International Conference on Noise and Vibration Engineering including USD2010, Leuven, Belgium, 20-22 September 2010. [Google Scholar]
- Ullate, Y.G. Estudio de Sistemas Ultrasónicos Basados en Multitransductores para la Detección de Defectos en Estructuras Tipo Placa. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2007. [Google Scholar]
- Schaal, C.; Samajder, H.; Baid, H.; Mal, A. Rayleigh to Lamb wave conversion at a delamination-like crack. J. Sound Vib. 2015, 353, 150–163. [Google Scholar] [CrossRef]
- Zhang, R.; Wan, M.; Cao, W. Parameter Measurement of Thin Elastic Layers Using Low-Frequency Multi-Mode Ultrasonic Lamb Waves. IEEE Trans. Instrum. Meas. 2001, 50, 1397–1403. [Google Scholar] [CrossRef]
- Zeroug, S.; Froelich, B. Ultrasonic leaky-Lamb wave imaging through a highly contrasting layer. In Proceedings of the IEEE Symposium on Ultrasonics, Honolulu, HI, USA, 5–8 October 2003; pp. 794–798. [Google Scholar]
- Bezdek, M.; Tittmann, B.R.; Joseph, K.L. Fluid-Coupled Waveguide for Leaky Guided Waves. In Proceedings of the 2006 IEEE Ultrasonics Symposium, Vancouver, BC, Canada, 3–6 October 2006. [Google Scholar]
- Balasubramaniam, K.; Rose, J.L. Physically Based Dispersion Curve Feature Analysis in the NDE of Composites. Res. Nondestruct. Eval. 1991, 3, 41–67. [Google Scholar] [CrossRef]
- Niethammer, M.; Jacobs, L.J.; Qu, J.; Jarzynski, J. Time-frequency representations of Lamb waves. J. Acoust. Soc. Am. 2001, 109, 1841–1847. [Google Scholar] [CrossRef]
- Kuttig, H.; Niethammer, M.; Hurlebaus, S.; Jacobs, L.J. Model-based analysis of dispersion curves using chirplets. J. Acoust. Soc. Am. 2006, 119, 2122–2130. [Google Scholar] [CrossRef]
- Prosser, W.H.; Seale, M.D.; Smith, B.T. Time-frequency analysis of the dispersion of Lamb modes. J. Acoust. Soc. Am. 1999, 105, 2669–2676. [Google Scholar] [CrossRef] [PubMed]
- Zima, B.; Rucka, M. Application of wavelet transform in analysis of guided wave propagation signals for damage detection in a steel plate. Diagnostyka 2015, 16, 43–48. [Google Scholar]
- Ray, P.; Manogharan, P.; Srinivasan, B.; Balasubramaniam, K.; Rajagopal, P. Novel Method of Defect Identification in Bent Structures through Feature-Guided Wave Detection using Fiber Bragg Grating Sensors. In Proceedings of the International Conference on Optical Fibre Sensors (OFS24), Curitiba, Brazil, 28 September–2 October 2015; Kalinowski, H.J., Fabris, J.L., Bock, W.J., Eds.; [Google Scholar]
- Genovés, V.; Gosálbez, J.; Carrión, A.; Miralles, R.; Payá, J. Optimized ultrasonic attenuation measures for non-homogeneous materials. Ultrasonics 2016, 65, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Alleyne, D.N.; Cawley, P. The Excitation of Lamb Waves in Pipes Using Dry-Coupled Piezoelectric Transducers. J. Nondestruct. Eval. 1996, 15, 11–20. [Google Scholar] [CrossRef]
- Hora, P.; Cervená, O. Determination of Lamb wave dispersion curves by means of Fourier transform. Appl. Comput. Mech. 2012, 6, 5–16. [Google Scholar]
- Ruiz, A.; Ortiz, N.; Medina, A.; Kim, J.-Y.; Jacobs, L.J. Application of ultrasonic methods for early detection of thermal damage in 2205 duplex stainless steel. NDT E Int. 2013, 54, 19–26. [Google Scholar] [CrossRef]
- Grondel, S.; Assaad, J.; Delebarre, C.; Blanquet, P.; Moulin, E. The propagation of Lamb waves in multilayered plates: phase-velocity measurement. Meas. Sci. Technol. 1999, 10, 348–353. [Google Scholar] [CrossRef]
- Goueygou, M.; Piwakowski, B. Radiation of surface waves into concrete by means of a wedge transducer: design and optimization. In Proceedings of the 16th World Conference on NDT (WCNDT), Montreal, QC, Canada, 30 August–3 September 2004. [Google Scholar]
- Goueygou, M.; Piwakowski, B.; Fnine, A.; Kaczmarek, M.; Buyle-Bodin, F. NDE of two-layered mortar samples using high-frequency Rayleigh waves. Ultrasonics 2004, 42, 889–895. [Google Scholar] [CrossRef]
- Kim, G.; Kim, J.-Y.; Kurtis, K.E.; Jacobs, L.J.; Le Pape, Y.; Guimaraes, M. Quantitative evaluation of carbonation in concrete using nonlinear ultrasound. Mater Struct 2016, 49, 399–409. [Google Scholar] [CrossRef]
- Deán, J.L.; Trillo, C.; López-Vázquez, J.C.; Doval, Á.F.; Fernández, J.L. Determination of the frequency spectrum of Lamb waves from a sequence of maps of the instantaneous acoustic displacement obtained with TV holography. In Proceedings of the SPIR 7389, Optical Measurement Systems for Industrial Inspection VI, Munich, Germany, 15–17 June 2009; Lehmann, P.H., Ed.; [Google Scholar]
- Carrión, A.; Genovés, V.; Pérez, G.; Payá, J.; Gosálbez, J. Flipped Accumulative Non-Linear Single Impact Resonance Acoustic Spectroscopy (FANSIRAS): A novel feature extraction algorithm for global damage assessment. J. Sound Vib. 2018, 432, 454–469. [Google Scholar] [CrossRef]
- Jain, A.; Greve, D.W.; Oppenheim, I.J. A MEMS Ultrasonic Transducer for Monitoring of Steel Structures. In Proceedings of the SPIE’s 9th Annual International Symposium on Smart Structures and Materials, San Diego, CA, USA, July 2002. [Google Scholar]
- Greve, D.W.; Oppenheim, I.J.; Zheng, P. Lamb Waves and Nearly-Longitudinal Waves in Thick Plates. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, San Diego, CA, USA, 8 April 2008; Tomizuka, M., Ed.; SPIE: Bellingham, WA, USA, 2008. [Google Scholar]
- Greve, D.W.; Zheng, P.; Oppenheim, I.J. Transition from Lamb waves to longitudinal waves in plates. Smart Mater. Struct. 2008, 17, 11. [Google Scholar] [CrossRef]
- Li, F.; Murayama, H.; Kageyama, K.; Shirai, T. Guided Wave and Damage Detection in Composite Laminates Using Different Fiber Optic Sensors. Sensors 2009, 9, 4005–4021. [Google Scholar] [CrossRef] [PubMed]
- Yan-Xun, X.; Fu-Zhen, X.; Ming-Xi, D. Evaluation of Thermal Degradation Induced Material Damage Using Nonlinear Lamb Waves. Chin. Phys. Lett. 2010, 27, 016202. [Google Scholar] [CrossRef]
- UNE-EN 196-1:2005. Métodos de Ensayo de Cementos; Parte 1: Determinación de resistencias mecánicas; Normalización Española: Madrid, Spain, 2005. [Google Scholar]
- Carrión, A.; Genovés, V.; Gosálbez, J.; Miralles, R.; Payá, J. Ultrasonic signal modality: A novel approach for concrete damage evaluation. Cem. Concr. Res. 2017, 101, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Goueygou, M.; Lafhaj, Z.; Soltani, F. Assessment of porosity of mortar using ultrasonic Rayleigh waves. NDT E Int. 2009, 42, 353–360. [Google Scholar] [CrossRef]
- Sancho-Knapik, D.; Calás, H.; Peguero-Pina, J.J.; Ramos Fernandez, A.; Gil-Pelegrín, E.; Álvarez-Arenas, T.E.G. Air-coupled Ultrasonic Resonant Spectroscopy for the Study of the Relationship Between Plant Leaves’ Elasticity and Their Water Content. IEEE Trans. Ultrason. Ferroelectr. 2012, 59, 319–325. [Google Scholar] [CrossRef]
- Álvarez-Arenas, T.E.G. Acoustic Impedance Matching of Piezoelectric Transducers to the Air. IEEE Trans. Ultrason. Ferroelectr. 2004, 51, 624–633. [Google Scholar] [CrossRef]
- Neuenschwander, J.; Schmidt, Th.; Lüthi, Th.; Romer, M. Leaky Rayleigh wave investigation on mortar samples. Ultrasonics 2006, 45, 50–55. [Google Scholar] [CrossRef]




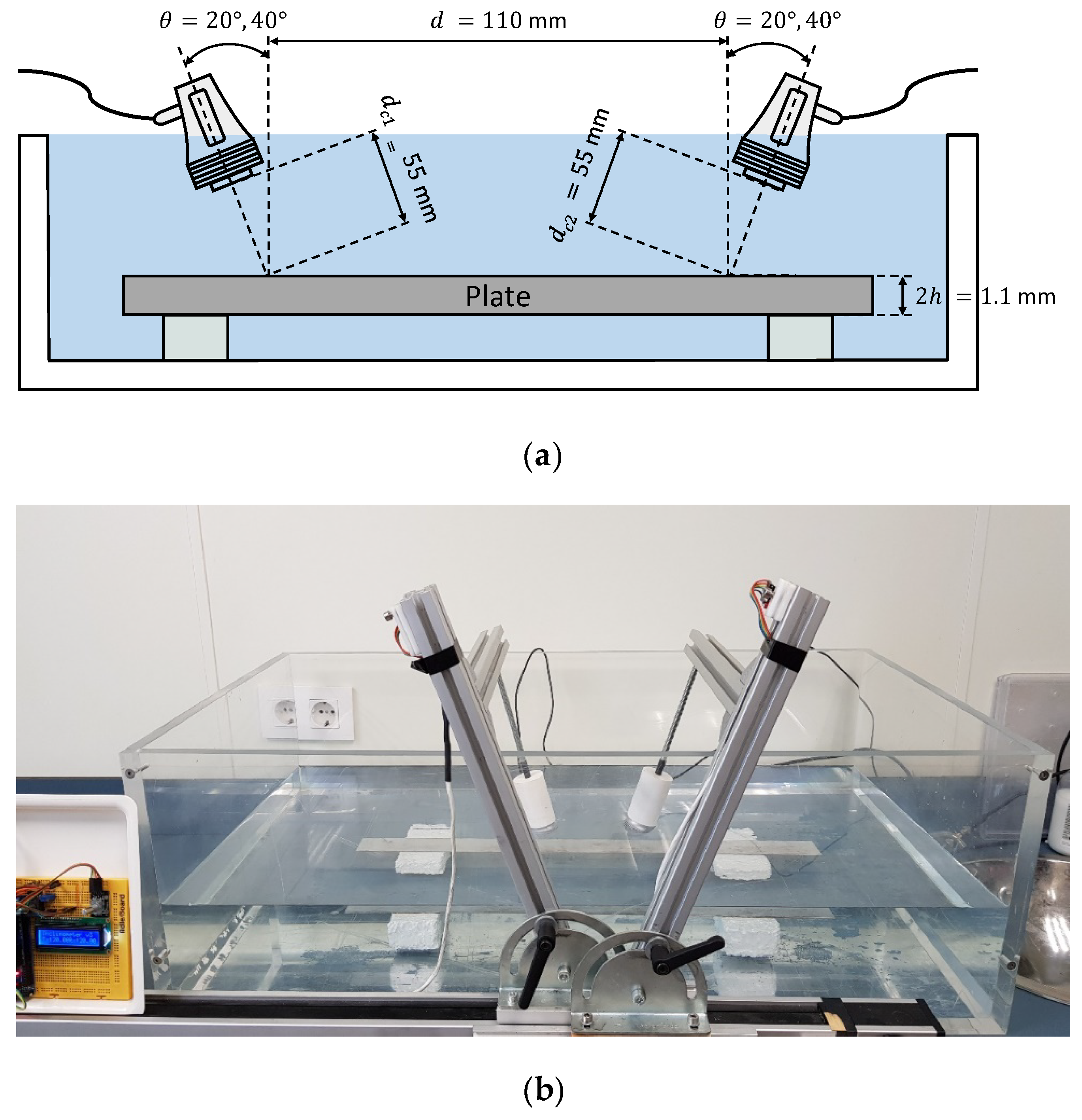
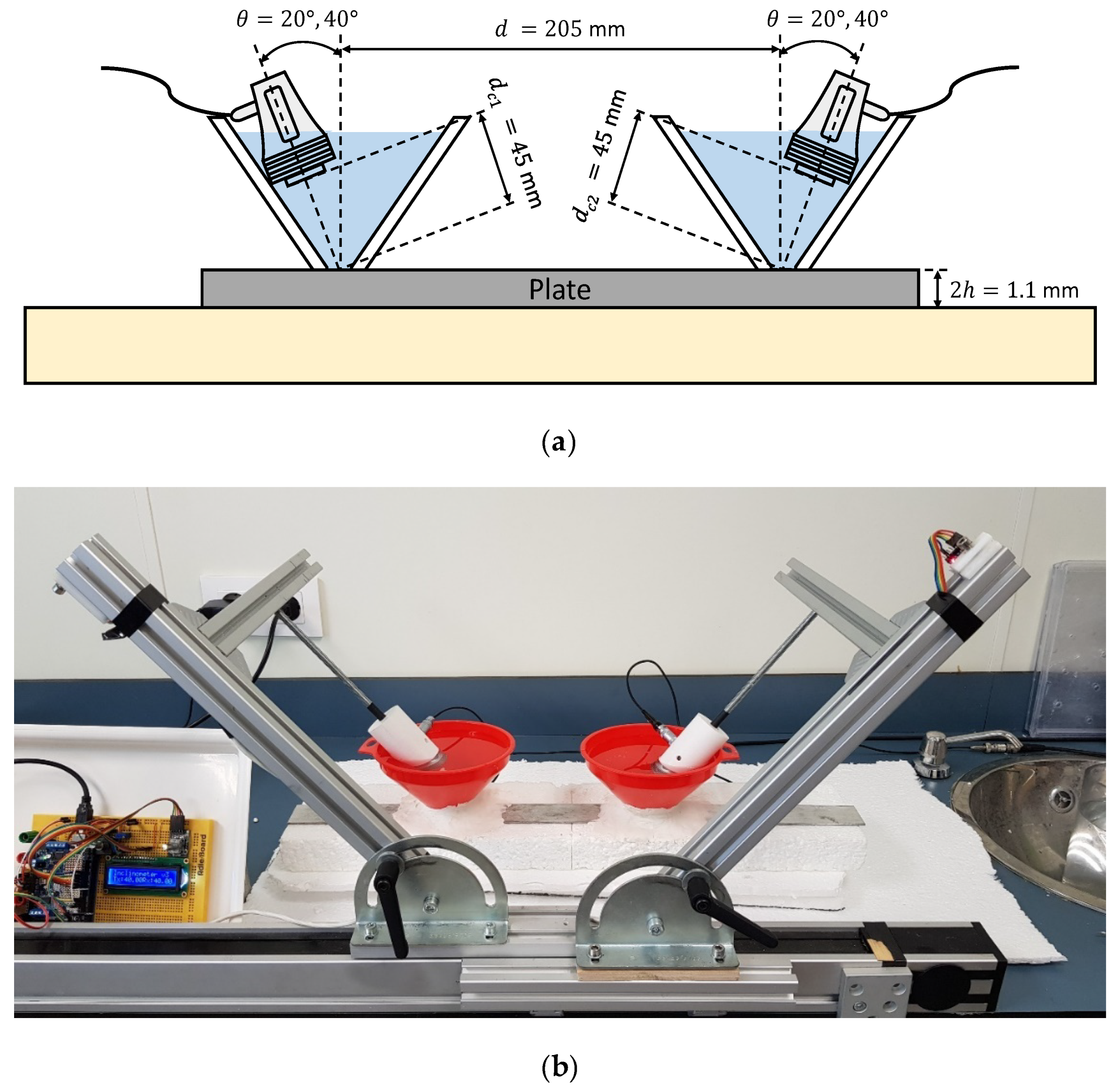


| Parameters | Stainless Steel | Mortar |
|---|---|---|
| Dimensions (length × width × thickness) (mm3) | 530 × 27 × 1.1 | 240 × 60 × 5 |
| Longitudinal wave velocity (m/s) | 5851 | 4779 |
| Transverse wave velocity (m/s) | 3056 | 2872 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vázquez, S.; Gosálbez, J.; Bosch, I.; Carrión, A.; Gallardo, C.; Payá, J. Comparative Study of Coupling Techniques in Lamb Wave Testing of Metallic and Cementitious Plates. Sensors 2019, 19, 4068. https://doi.org/10.3390/s19194068
Vázquez S, Gosálbez J, Bosch I, Carrión A, Gallardo C, Payá J. Comparative Study of Coupling Techniques in Lamb Wave Testing of Metallic and Cementitious Plates. Sensors. 2019; 19(19):4068. https://doi.org/10.3390/s19194068
Chicago/Turabian StyleVázquez, Santiago, Jorge Gosálbez, Ignacio Bosch, Alicia Carrión, Carles Gallardo, and Jordi Payá. 2019. "Comparative Study of Coupling Techniques in Lamb Wave Testing of Metallic and Cementitious Plates" Sensors 19, no. 19: 4068. https://doi.org/10.3390/s19194068
APA StyleVázquez, S., Gosálbez, J., Bosch, I., Carrión, A., Gallardo, C., & Payá, J. (2019). Comparative Study of Coupling Techniques in Lamb Wave Testing of Metallic and Cementitious Plates. Sensors, 19(19), 4068. https://doi.org/10.3390/s19194068







