A Qualitative Analysis of a USB Camera for AGV Control
Abstract
:1. Introduction
2. Related Works
3. Materials and Methods
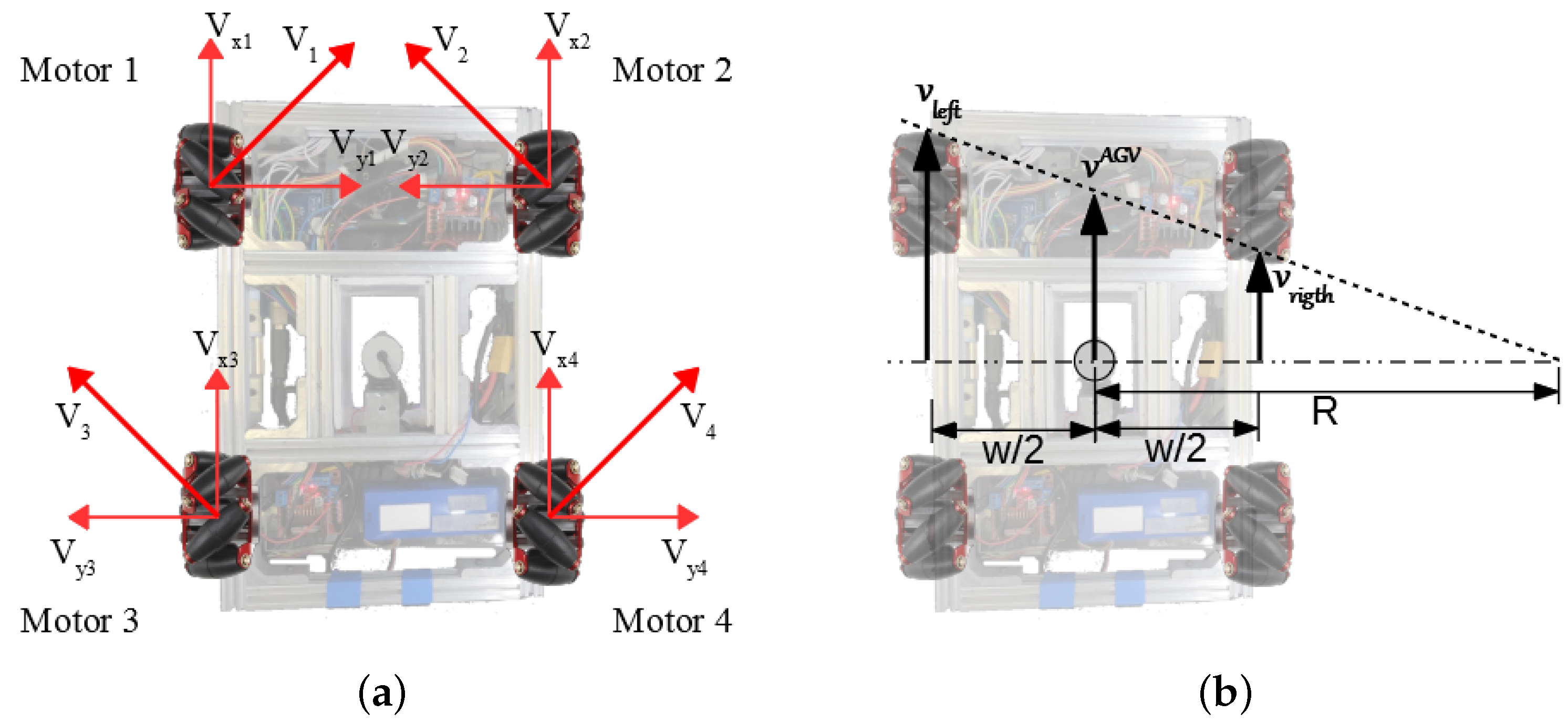
3.1. Automated Guided Vehicle with Mecanum Wheels
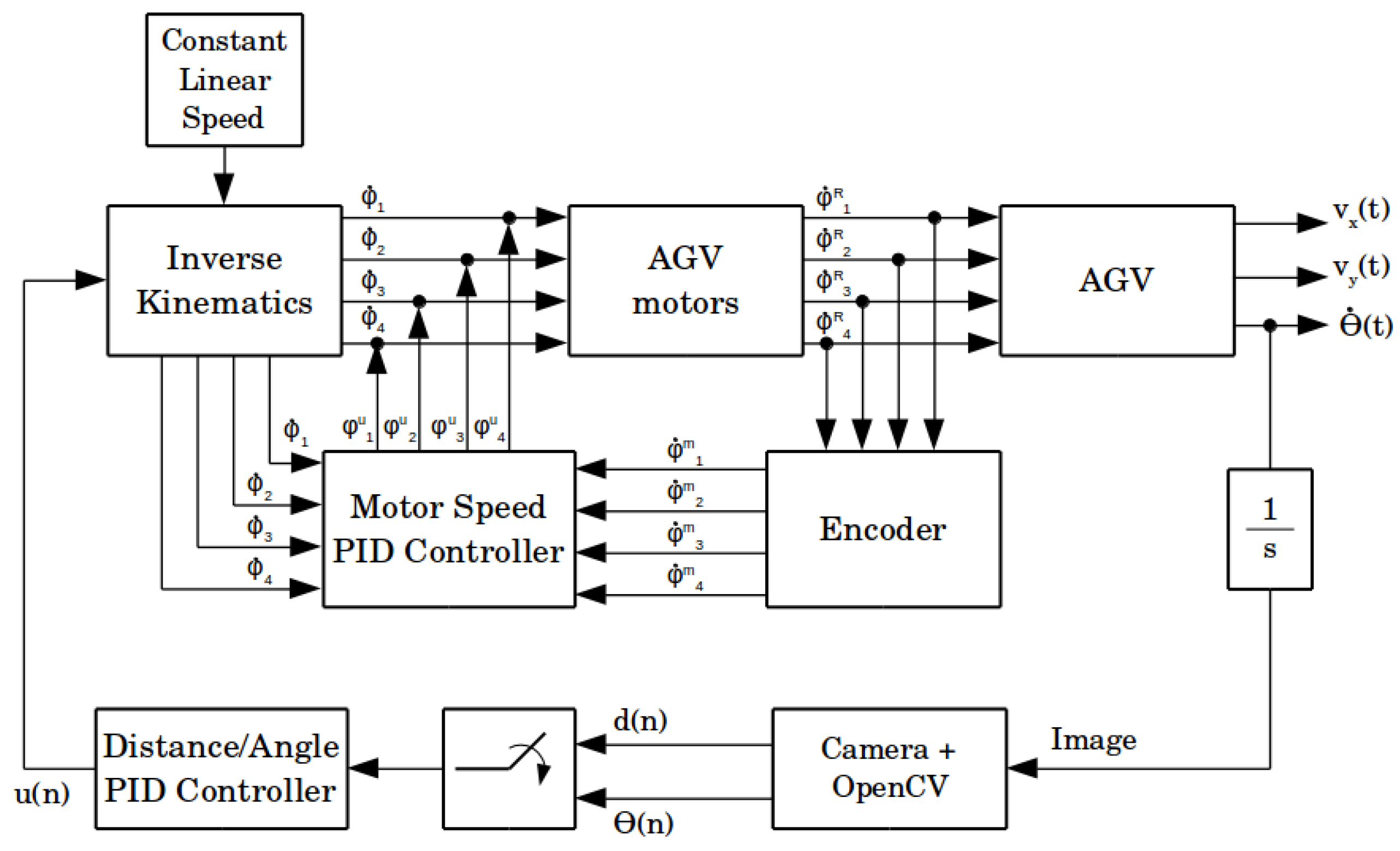
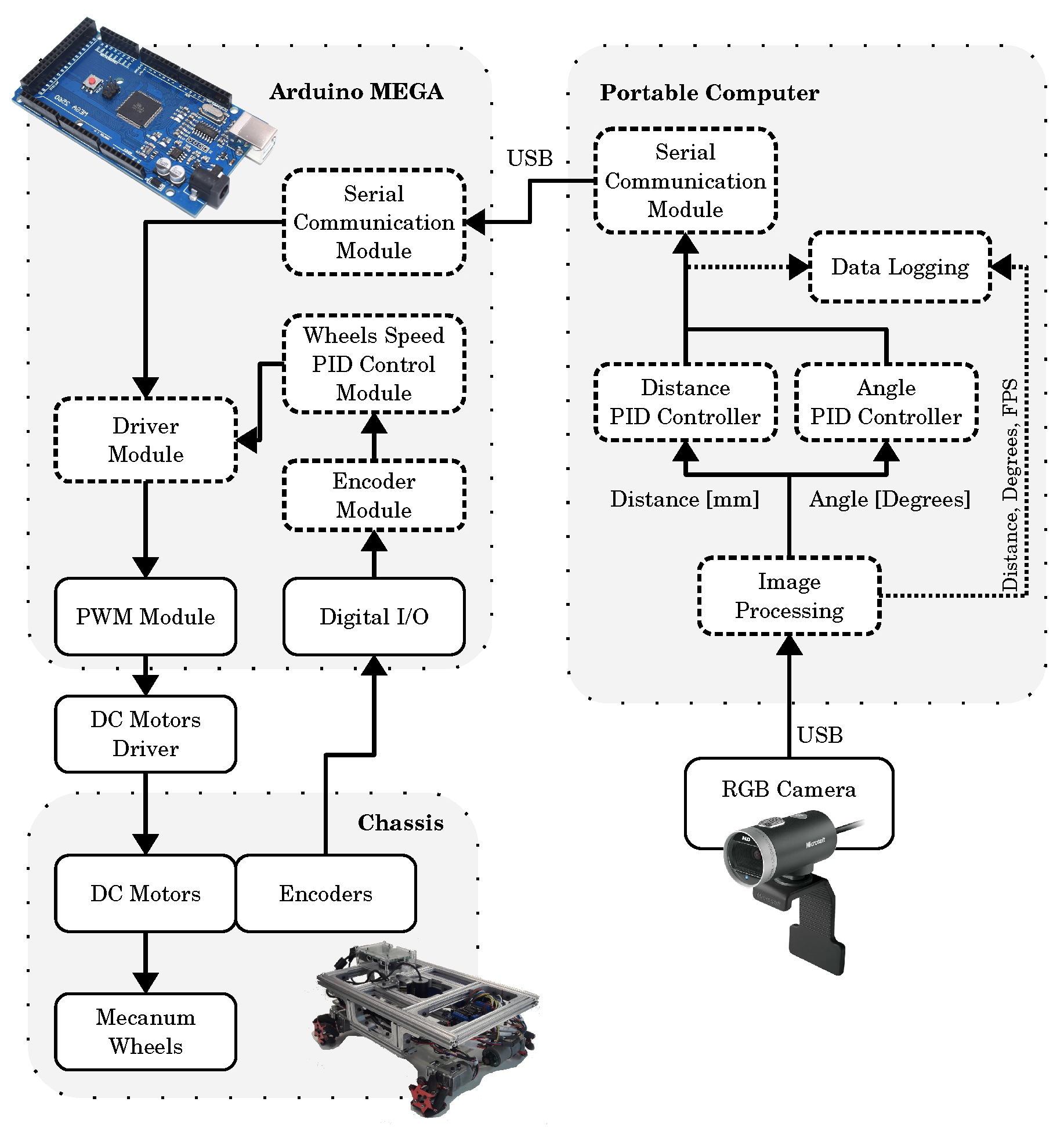
3.2. Control Systems
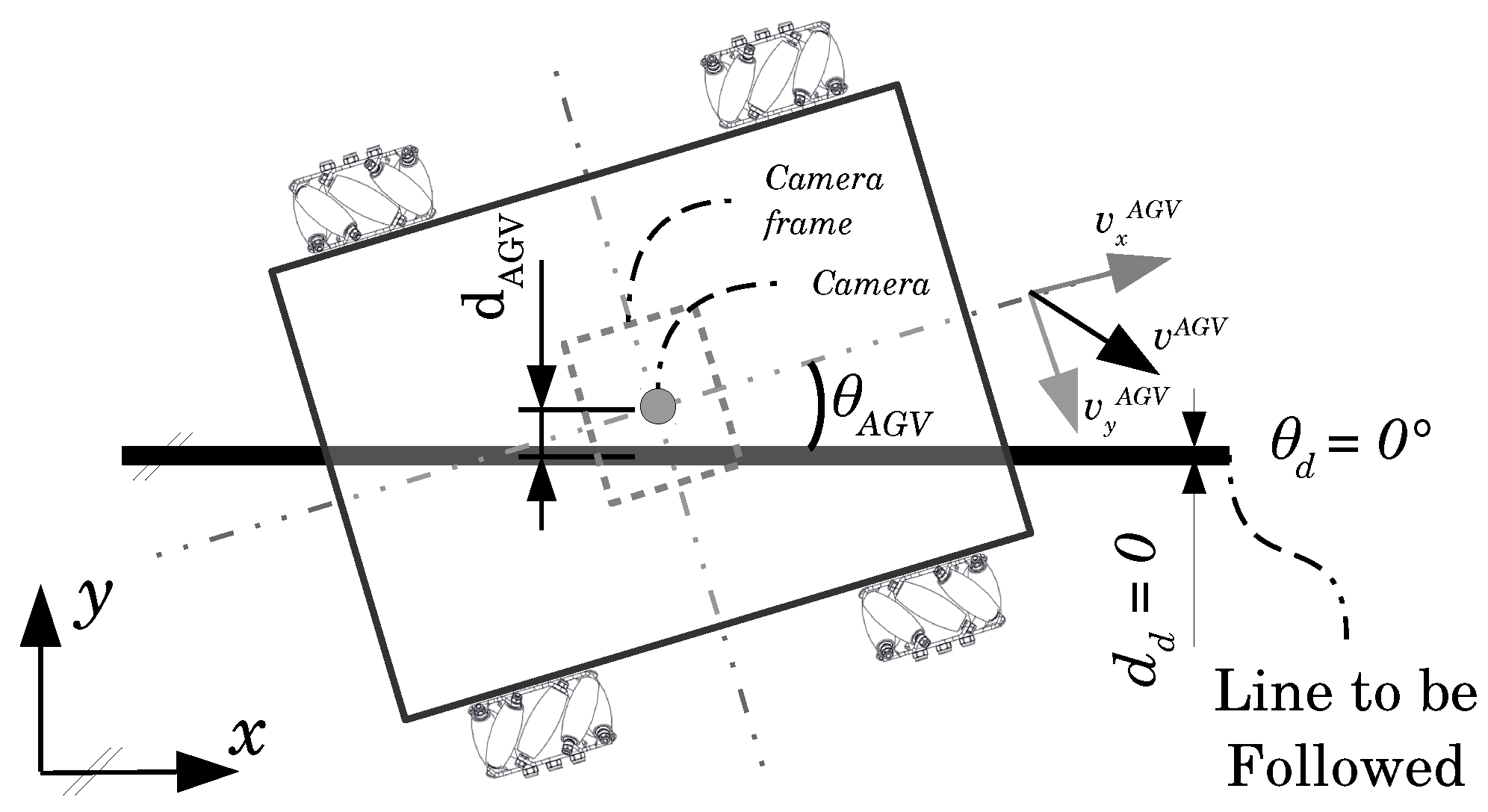
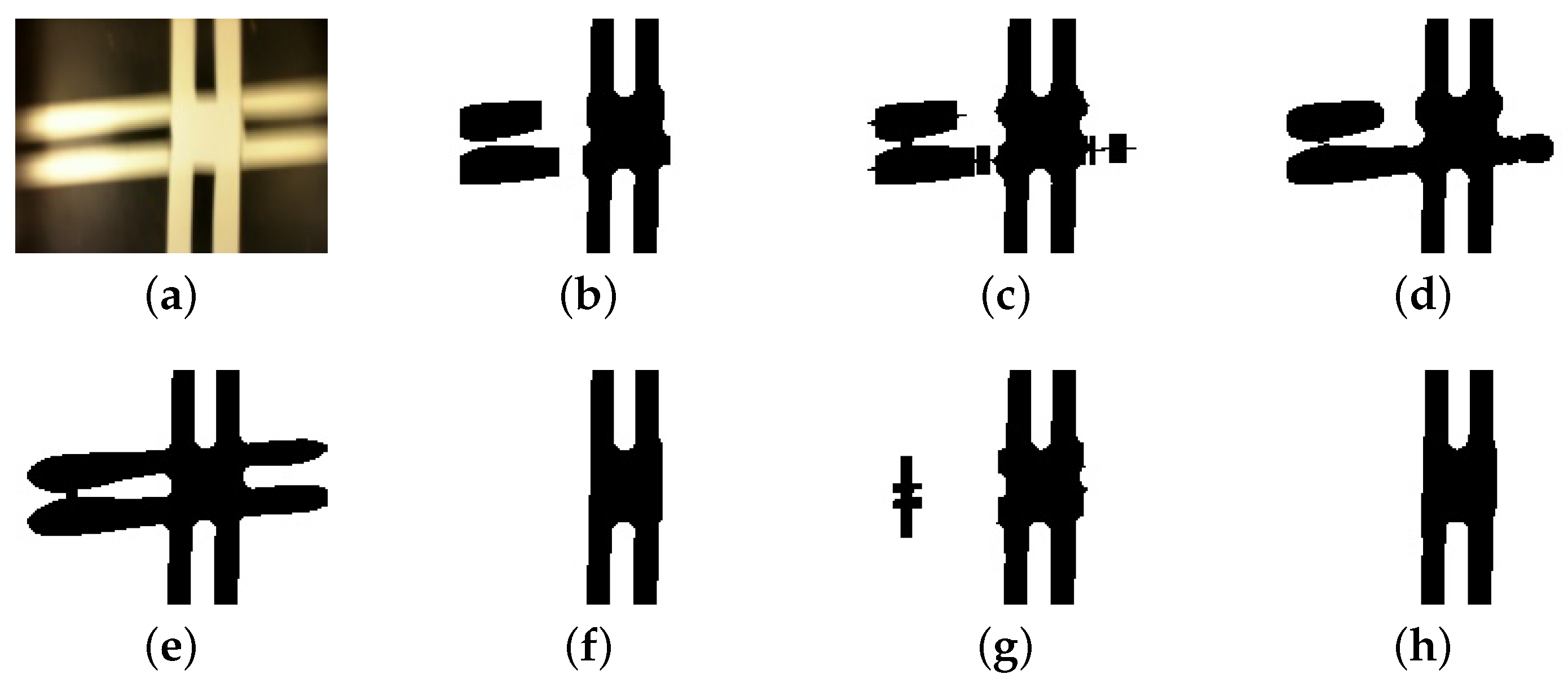
3.3. Line Detection and Measurement Algorithm
3.3.1. Image Noise Elimination Techniques
| Algorithm 1: Median Filter Algorithm according to Trucco and Verri [26]. |
 |
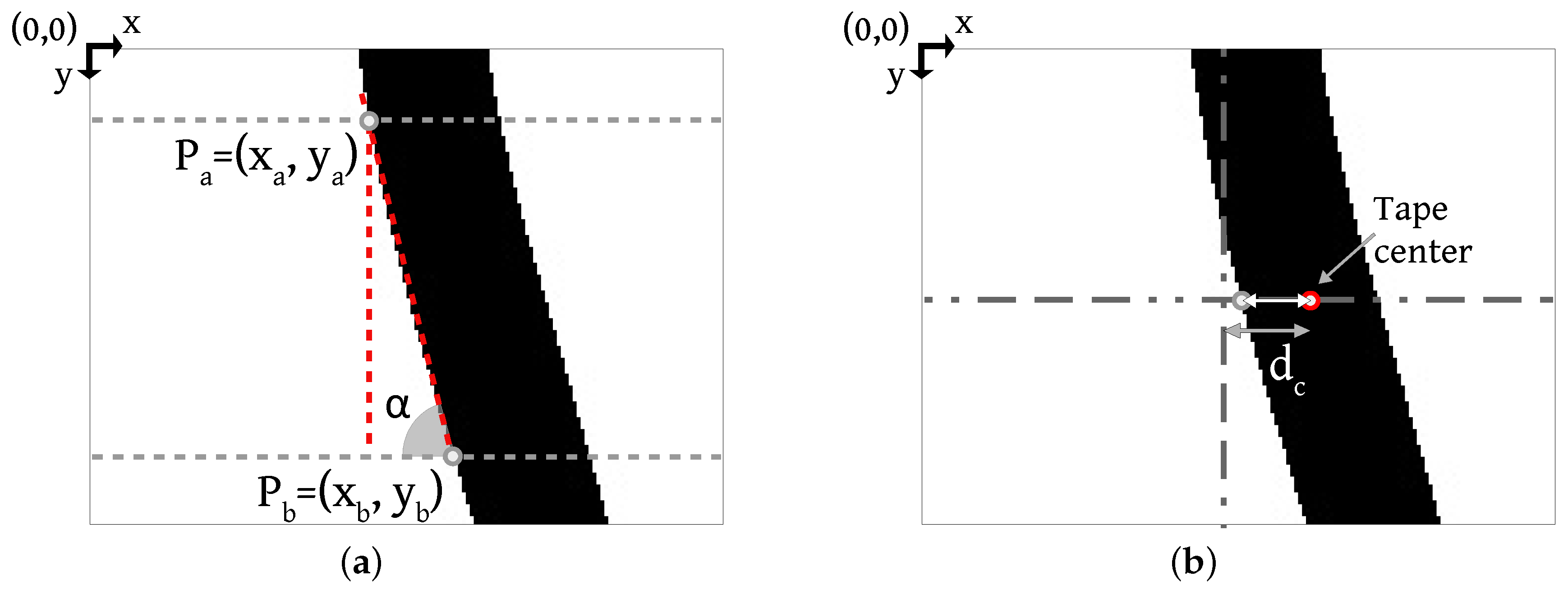
3.3.2. Angle and Distance Measurement
| Algorithm 2: Reference line angle determination. |
 |
| Algorithm 3: Reference line distance from center determination. |
 |
3.4. Definition of Validation Indicators
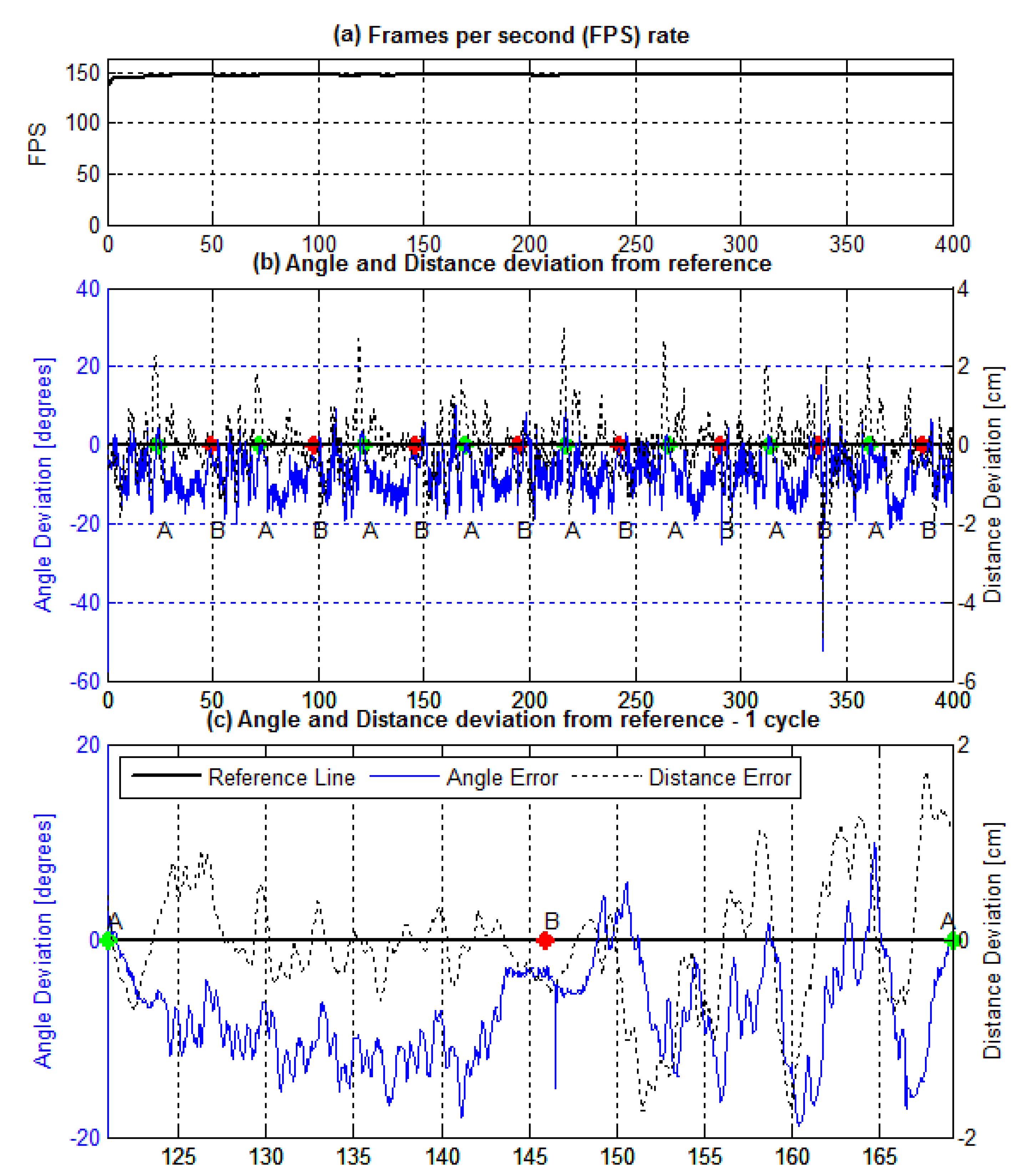
4. Experimentation
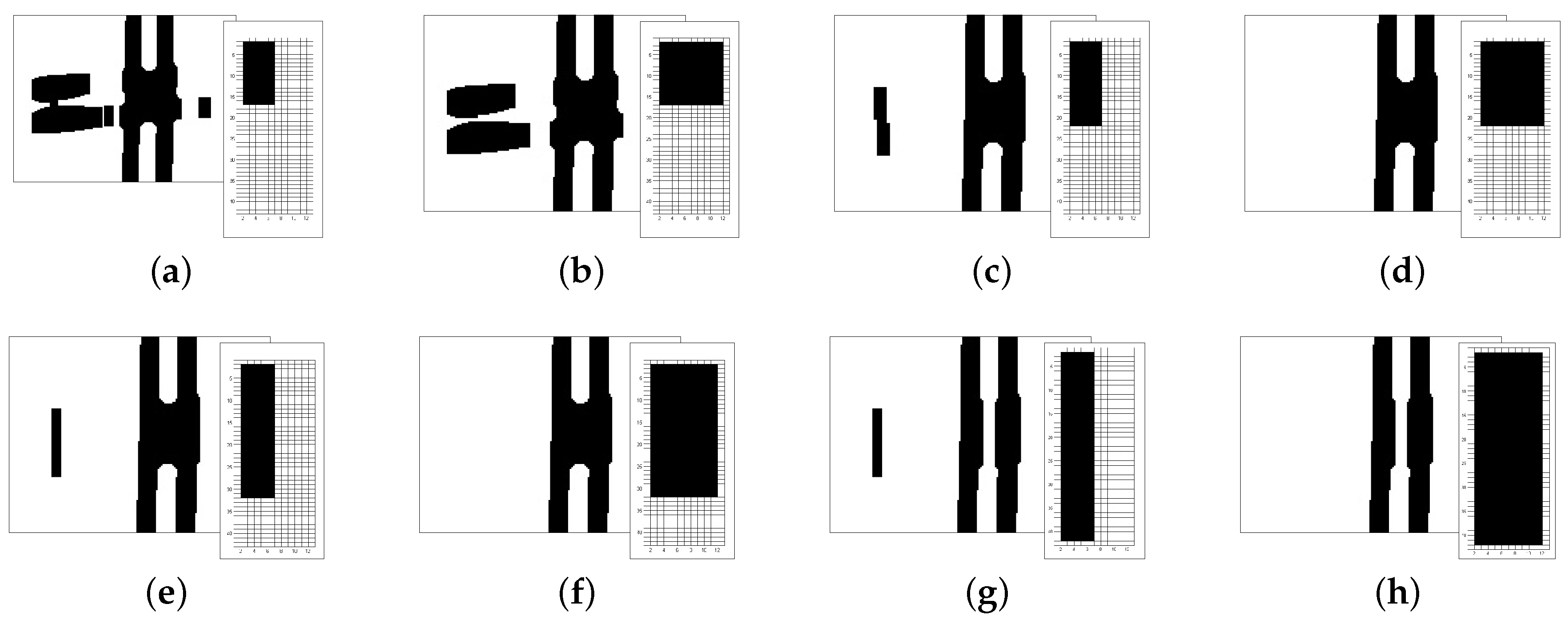
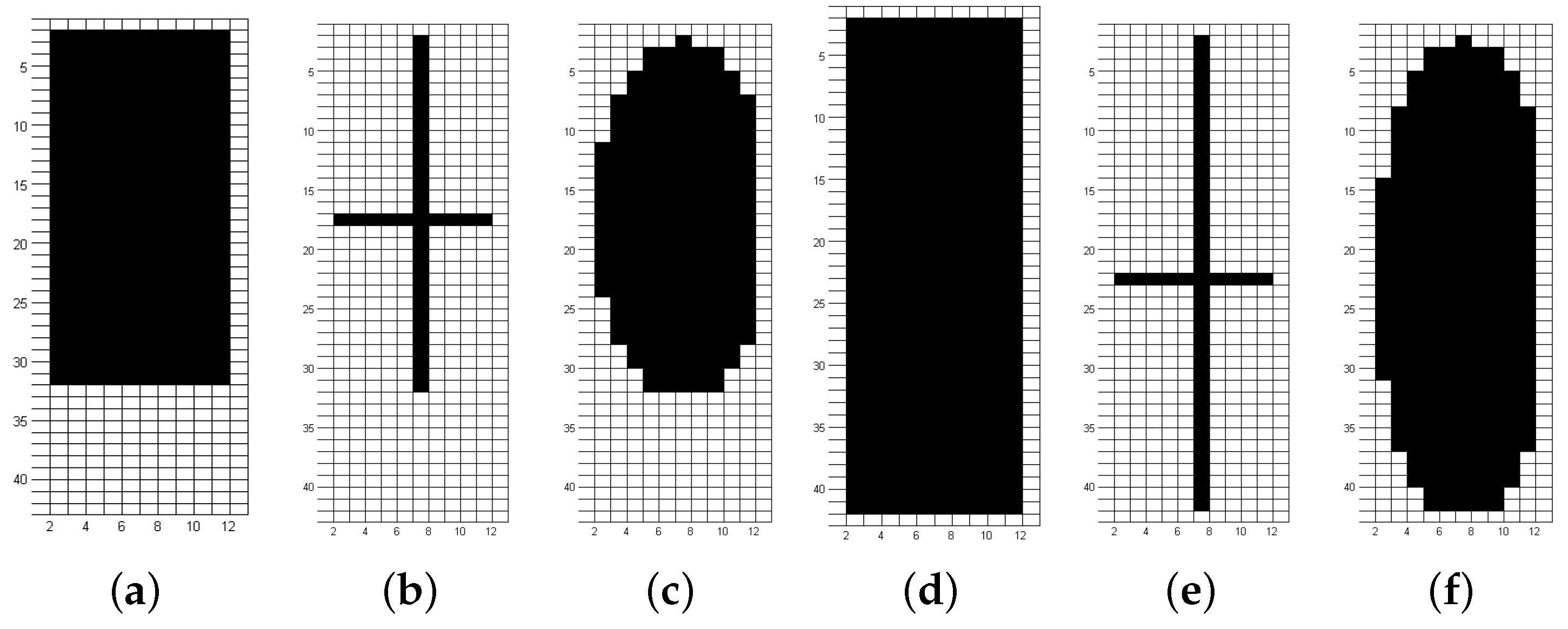
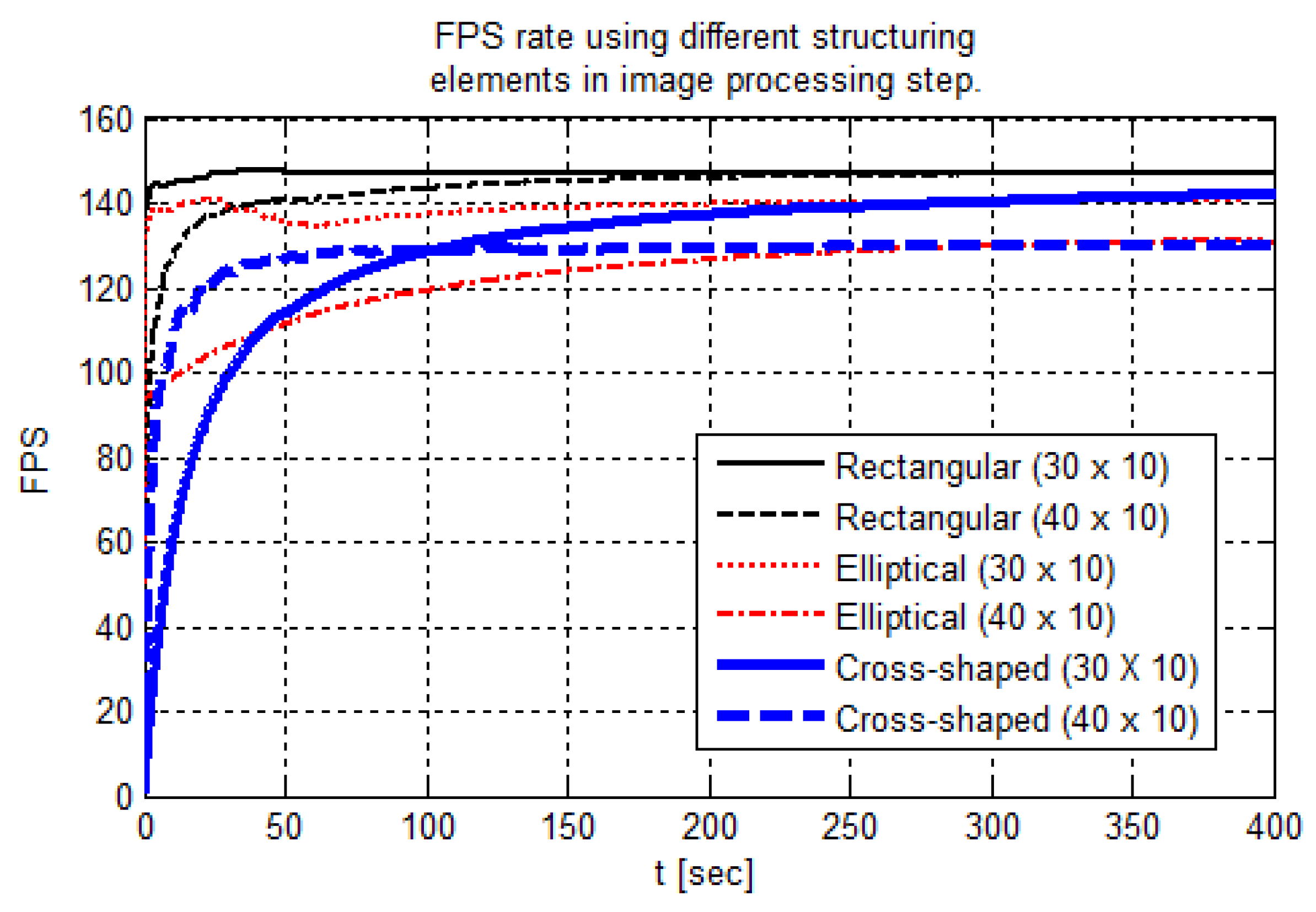
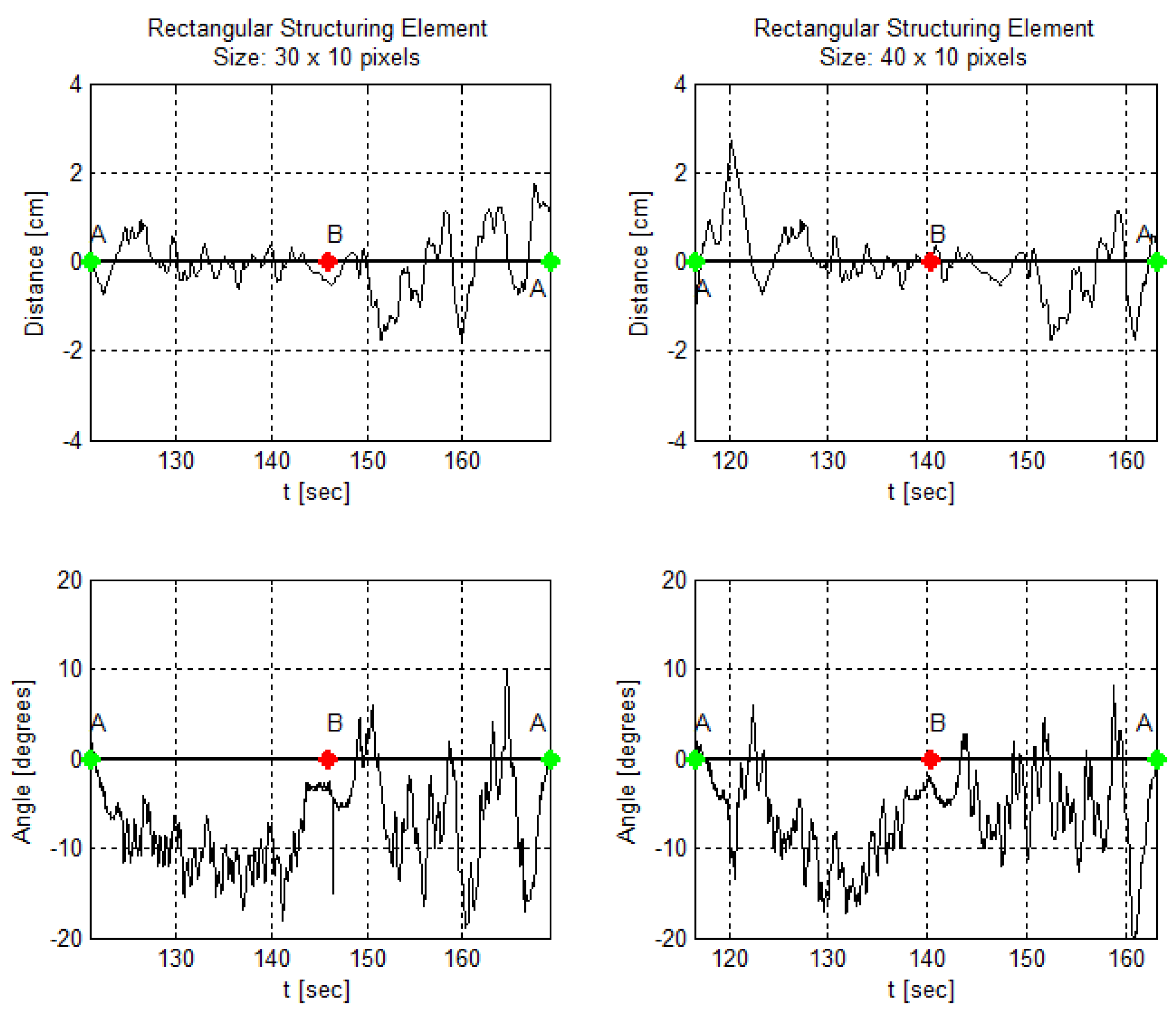
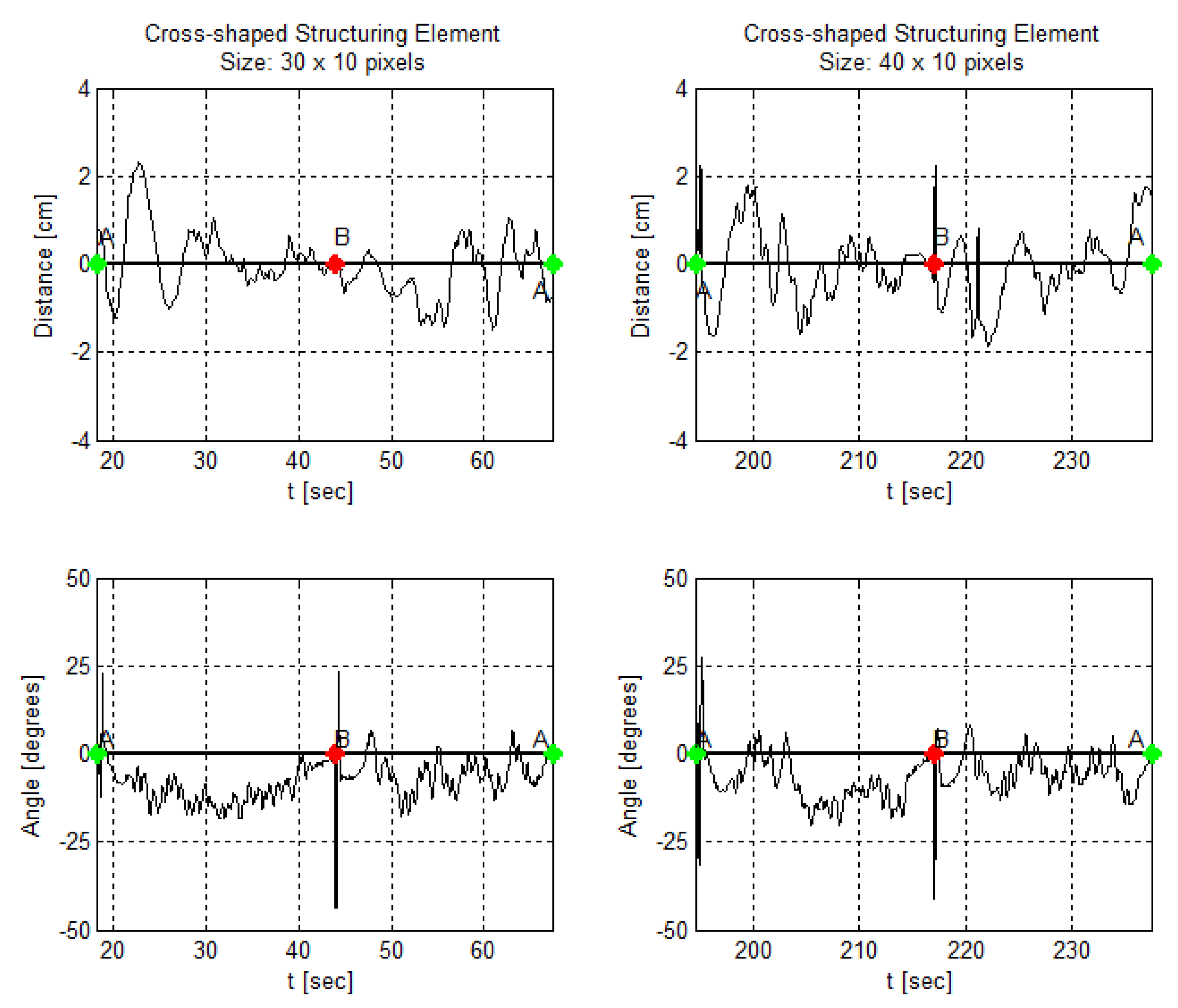
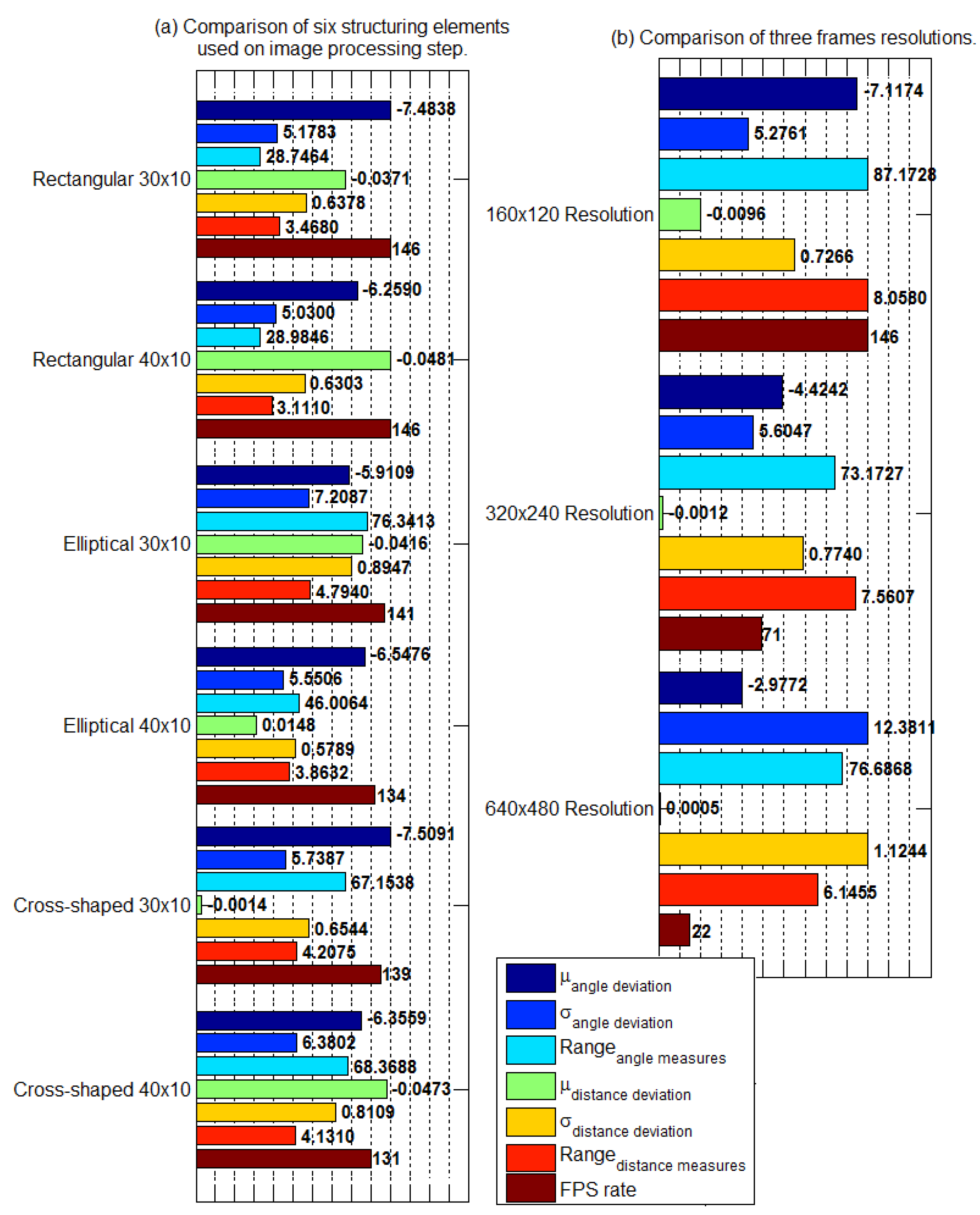
4.1. Kernel Shape and Size Variation
4.2. AGV Speed Variation
4.3. Image Resolution Variation
4.4. Experimental Results
4.4.1. Kernel Shape and Size Variation
4.4.2. AGV Speed Variation
4.4.3. Image Resolution Variation
5. Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| AGV | Automated Guided Vehicles |
| RGB | Red–Green–Blue |
| RFID | Radio Frequency Identification |
| AGC | Automated Guided Cart |
| LiDAR | Light Detection and Ranging |
| QR Code | Quick Response Code |
| ARM | Advanced RISC Machine |
| RISC | Reduced Instruction Set Computer |
| PID | Proportional Integral Derivative |
| PWM | Pulse Width Modulation |
| fps | Frames per Second |
References
- Andersen, R.E.; Hansen, E.B.; Cerny, D.; Madsen, S.; Pulendralingam, B.; Bøgh, S.; Chrysostomou, D. Integration of a skill-based collaborative mobile robot in a smart cyber-physical environment. Procedia Manuf. 2017, 11, 114–123. [Google Scholar] [CrossRef]
- Guizzo, E. Three engineers, hundreds of robots, one warehouse. IEEE Spectrum 2008, 45, 26–34. [Google Scholar] [CrossRef]
- Caridá, V.; Morandin, O.; Tuma, C. Approaches of fuzzy systems applied to an AGV dispatching system in a FMS. Int. J. Adv. Manuf. Technol. 2015, 79, 615–625. [Google Scholar] [CrossRef]
- Yuye, Z. Path Following Control of Automatic Guided Vehicle based on Hierarchical Fuzzy Algorithm. J. Theor. Appl. Inf. Technol. 2013, 48, 1126–1130. [Google Scholar]
- Fedorko, G.; Honus, S.; Salai, R. Comparison of the Traditional and Autonomous AGV Systems. MATEC Web Conf. 2017, 134, 13. [Google Scholar] [CrossRef] [Green Version]
- RoboteQ. Precision Magnetic Track Following Sensor with Gyrosope. Available online: https://www.roboteq.com/index.php/docman/magsensor-documents-and-files/mgs-documents-1/mgs-datasheets-1/mgs1600-datasheet (accessed on 12 December 2018).
- Li, L.; Liu, Y.H.; Fang, M.; Zheng, Z.; Tang, H. Vision-based intelligent forklift Automatic Guided Vehicle (AGV). In Proceedings of the 2015 IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 24–28 August 2015; pp. 264–265. [Google Scholar]
- Xing, W.; Peihuang, L.; Jun, Y.; Xiaoming, Q.; Dunbing, T. Intersection recognition and guide-path selection for a vision-based AGV in a bidirectional flow network. Int. J. Adv. Robot. Syst. 2014, 11. [Google Scholar] [CrossRef]
- Cawood, G.J.; Gorlach, I.A. Navigation and locomotion of a low-cost Automated Guided Cart. In Proceedings of the Pattern Recognition Association of South Africa and Robotics and Mechatronics International Conference (PRASA-RobMech), Port Elizabeth, South Africa, 26–27 November 2015; pp. 83–88. [Google Scholar]
- Henebrey, J.; Gorlach, I. Enhancement of an Automated Guided Cart. In Proceedings of the Pattern Recognition Association of South Africa and Robotics and Mechatronics International Conference (PRASA-RobMech), Stellenbosch, South Africa, 30 November–2 December 2016; pp. 1–5. [Google Scholar]
- Wei, P.; Cagle, L.; Reza, T.; Ball, J.; Gafford, J. LiDAR and camera detection fusion in a real-time industrial multi-sensor collision avoidance system. Electronics 2018, 7, 84. [Google Scholar] [CrossRef]
- Yu, J.; Lou, P.; Wu, X. A dual-core real-time embedded system for vision-based automated guided vehicle. In Proceedings of the 2009 IITA International Conference on Control, Automation and Systems Engineering, Zhangjiajie, China, 11–12 July 2009; pp. 207–211. [Google Scholar]
- Lee, J.W.; Choi, S.U.; Lee, C.H.; Lee, Y.J.; Lee, K.S. A study for AGV steering control and identification using vision system. In Proceedings of the 2001 IEEE International Symposium on Industrial Electronics Proceedings, Pusan, South Korea, 12–16 June 2001; pp. 1575–1578. [Google Scholar]
- Horan, B.; Najdovski, Z.; Black, T.; Nahavandi, S.; Crothers, P. OzTug mobile robot for manufacturing transportation. In Proceedings of the 2011 IEEE International Conference on Systems, Man, and Cybernetics, Anchorage, AK, USA, 9–12 October 2011; pp. 3554–3560. [Google Scholar]
- Wang, C.; Wang, L.; Qin, J.; Wu, Z.; Duan, L.; Cao, M.; Li, Z.; Lu, Z.; Ling, Y.; Li, M.; et al. Development of a vision navigation system with Fuzzy Control Algorithm for Automated Guided Vehicle. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 2077–2082. [Google Scholar]
- Liu, J.; Zhong, X.; Peng, X.; Tian, J.; Zou, C. Design and Implementation of New AGV System Based on Two-layer Controller Structure. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 5340–5346. [Google Scholar]
- Wu, X.; Zhang, Y.; Zou, T.; Zhao, L.; Lou, P.; Yin, Z. Coordinated path tracking of two vision-guided tractors for heavy-duty robotic vehicles. Robot. Comput. Integr. Manuf. 2018, 53, 93–107. [Google Scholar] [CrossRef]
- Kondákor, A.; Törcsvari, Z.; Nagy, Á.; Vajk, I. A Line Tracking Algorithm Based on Image Processing. In Proceedings of the 2018 IEEE 12th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 17–19 May 2018; pp. 39–44. [Google Scholar]
- Kang, J.; Lee, J.; Eum, H.; Hyun, C.H.; Park, M. An application of parameter extraction for AGV navigation based on computer vision. In Proceedings of the 2013 10th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Jeju, South Korea, 30 October–2 November 2013; pp. 622–626. [Google Scholar]
- Gumus, O.; Topaloglu, M.; Ozcelik, D. The use of computer controlled line follower robots in public transport. Procedia Comput. Sci. 2016, 102, 202–208. [Google Scholar] [CrossRef]
- Mautz, R.; Tilch, S. Survey of optical indoor positioning systems. In Proceedings of the 2011 International Conference on Indoor Positioning and Indoor Navigation, Guimaraes, Portugal, 21–23 September 2011; pp. 1–7. [Google Scholar]
- Zhou, C.; Liu, X. The study of applying the AGV navigation system based on two dimensional bar code. In Proceedings of the 2016 International Conference on Industrial Informatics - Computing Technology, Intelligent Technology, Industrial Information Integration (ICIICII), Wuhan, China, 3–4 December 2016; pp. 206–209. [Google Scholar]
- Wu, X.; Xu, M.; Wang, L. Differential speed steering control for four-wheel independent driving electric vehicle. In Proceedings of the 2013 IEEE International Symposium on Industrial Electronics, Taipei, Taiwan, 28–31 May 2013; pp. 1–6. [Google Scholar]
- De Oliveira, D.P. Estratégia De Modelagem Da Dinâmica De Controladores Para Controle De AGV [Controller Dynamics Modeling Strategy for the AGV Control]. Master’s Thesis, Universidade Federal de São Carlos, São Carlos, SP, Brazil, 2018. [Google Scholar]
- Bradski, G. The OpenCV Library. Dr. Dobb’s J. Softw. Tools 2000, 120, 122–125. Available online: https://opencv.org/ (accessed on 15 September 2019).
- Trucco, E.; Verri, A. Introductory Techniques for 3D Computer Vision; Prentice Hall Englewood Cliffs: New Jersey, NJ, USA, 1998. [Google Scholar]


















| Description | Quantity |
|---|---|
| AGV Body Length | 310 mm |
| AGV Body Width | 200 mm |
| AGV Body Height | 130 mm |
| Wheel Diameter | 54 mm |
| Max. Linear Velocity of the AGV Body | 0.58 m/s |
| Mass of AGV Body | 3.4 kg |
| Features | Microsoft LifeCam Cinema Model: H5D-00013 |
|---|---|
| Still Resolution | 5 Megapixels |
| Video Modes | 1280 × 720 pixels video |
| Lens | Wide-angle lens |
| Sensor Technology\ Model | CMOS image sensor\ Not disclosed |
| Fixed Focus | from ∼0.15 m to infinity |
| Field of View | 73° diagonal field of view |
| Max. Frame rate | 30 fps |
| Interface | USB 2.0 |
| Image Features | Digital pan, tilt, and 4x digital zoom; Auto focus; Automatic image adjustment with manual override. |
| Description | Quantity |
|---|---|
| d | cm |
| Width x Length | pixels |
| 73° | |
| approx. cm/pixel | |
| angle resolution | approx. 0.603°/pixel |
| Processor | Intel® Core™ i7-3630QM CPU @ 2.40 GHz x 8 |
| Graphics | Intel® Ivybridge Mobile |
| RAM memory | 4 GB |
| Operational System | Ubuntu 16.04 LTS |
| Python version | 2.7.12 |
| OpenCV library | 3.3.1 |
| Description | Quantity | Description | Quantity | |
|---|---|---|---|---|
| d | cm | d | cm | |
| pixels | pixels | |||
| 73° | 73° | |||
| approx. cm/pixel | approx. cm/pixel | |||
| Angle resolution | approx. 0.163°/pixel | Angle resolution | approx. 0.318°/pixel |
| Kernel Shape | Rectangular | Elliptical | Cross-Shaped | |||
|---|---|---|---|---|---|---|
| Kernel Size [pixels] | ||||||
| Angle Deviation Mean | −7.4838 | −6.259 | −5.9109 | −6.5476 | −7.5091 | −6.3559 |
| Angle Deviation Standard Deviation | 5.1783 | 5.03 | 7.2087 | 5.5506 | 5.7387 | 6.3802 |
| Angle Measurements Range [degrees] | 28.7464 | 28.9846 | 76.3413 | 46.0064 | 67.1538 | 68.3688 |
| Distance Deviation Mean | −0.0371 | −0.0481 | −0.0416 | 0.0148 | −0.0014 | −0.0473 |
| Distance Deviation Standard Deviation | 0.6378 | 0.6303 | 0.8947 | 0.5789 | 0.6544 | 0.8109 |
| Distance Measurements Range [cm] | 3.468 | 3.111 | 4.794 | 3.8632 | 4.2075 | 4.131 |
| fps rate | 146 | 146 | 141 | 134 | 139 | 131 |
| Image Resolution [pixels] | |||
|---|---|---|---|
| Angle Deviation Mean | −7.1174 | −4.4242 | −2.9772 |
| Angle Deviation Standard Deviation | 5.2761 | 5.6047 | 12.3811 |
| Angle Measurements Range [degrees] | 87.1728 | 73.1727 | 76.6868 |
| Distance Deviation Mean | −0.0096 | −0.0012 | −0.0005 |
| Distance Deviation Standard Deviation | 0.7266 | 0.774 | 1.1244 |
| Distance Measurements Range [cm] | 8.058 | 7.5607 | 6.1455 |
| fps rate | 146 | 71 | 22 |
| Linear Speed [m/s] | 0.08 | 0.11 | 0.15 | 0.18 | 0.21 |
|---|---|---|---|---|---|
| Angle Deviation Mean | −9.5431 | −9.2255 | −8.2625 | −8.0161 | −7.4838 |
| Angle Deviation Standard Deviation | 7.6585 | 5.1106 | 4.9409 | 5.2089 | 5.1783 |
| Angle Measurements Range [degrees] | 88.1462 | 28.2526 | 28.1629 | 42.7565 | 28.7464 |
| Distance Deviation Mean | −0.0342 | −0.0357 | −0.0527 | −0.0666 | −0.0371 |
| Distance Deviation Standard Deviation | 0.6886 | 0.4713 | 0.5179 | 0.7159 | 0.6378 |
| Distance Measurements Range [cm] | 7.1655 | 4.335 | 4.029 | 5.7502 | 3.468 |
| fps rate | 130 | 136 | 124 | 130 | 146 |
| Linear Speed [m/s] | 0.21 | 0.23 | 0.25 | 0.26 | 0.29 |
|---|---|---|---|---|---|
| Angle Deviation Mean | −7.4838 | −9.1616 | −7.9728 | −8.388 | −8.6504 |
| Angle Deviation Standard Deviation | 5.1783 | 5.9414 | 7.4547 | 7.8457 | 10.185 |
| Angle Measurements Range [degrees] | 28.7464 | 56.1869 | 90.0964 | 95.2142 | 134.9394 |
| Distance Deviation Mean | −0.0371 | −0.0408 | −0.0257 | −0.7328 | −0.5598 |
| Distance Deviation Standard Deviation | 0.6378 | 0.8898 | 1.1358 | 1.838 | 1.8675 |
| Distance Measurements Range [cm] | 3.468 | 7.599 | 7.854 | 7.854 | 7.8349 |
| fps rate | 146 | 129 | 139 | 148 | 136 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puppim de Oliveira, D.; Pereira Neves dos Reis, W.; Morandin Junior, O. A Qualitative Analysis of a USB Camera for AGV Control. Sensors 2019, 19, 4111. https://doi.org/10.3390/s19194111
Puppim de Oliveira D, Pereira Neves dos Reis W, Morandin Junior O. A Qualitative Analysis of a USB Camera for AGV Control. Sensors. 2019; 19(19):4111. https://doi.org/10.3390/s19194111
Chicago/Turabian StylePuppim de Oliveira, Diogo, Wallace Pereira Neves dos Reis, and Orides Morandin Junior. 2019. "A Qualitative Analysis of a USB Camera for AGV Control" Sensors 19, no. 19: 4111. https://doi.org/10.3390/s19194111
APA StylePuppim de Oliveira, D., Pereira Neves dos Reis, W., & Morandin Junior, O. (2019). A Qualitative Analysis of a USB Camera for AGV Control. Sensors, 19(19), 4111. https://doi.org/10.3390/s19194111






