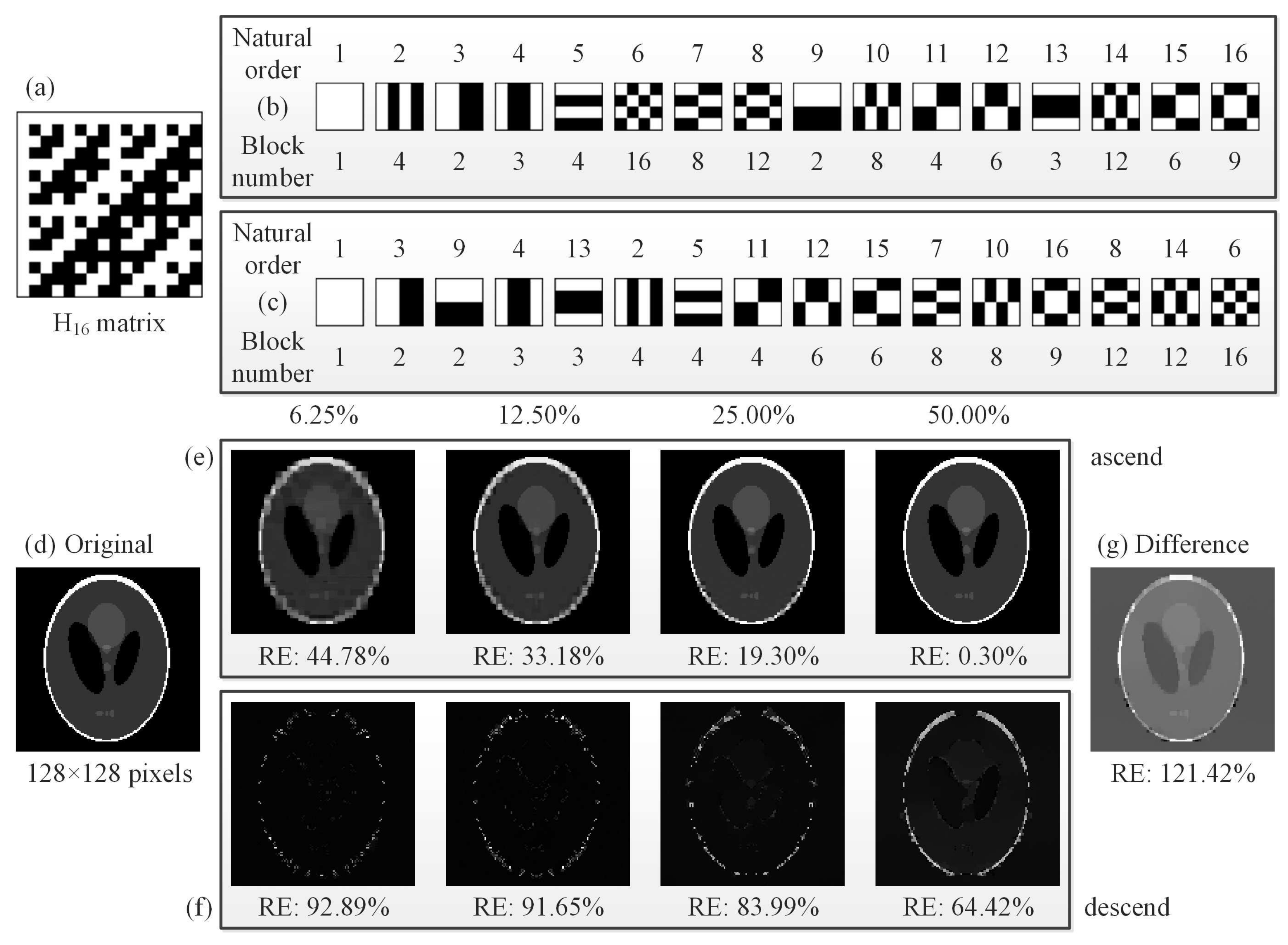
3.1. Numerical Simulations
To test the performance of our method for image reconstruction, some numerical simulations were performed. Here, we introduce another unitless performance measure, the peak signal-to-noise ratio (PSNR), which is defined as
where
. The MSE describes the squared distance between the recovered image and the original image. Naturally, the larger is the PSNR value, the better is the quality of the image recovered. To allow a fair comparison of the image quality, all the recovered images in
Figure 1,
Figure 2 and
Figure 5,
Figure 6,
Figure 7 and
Figure 8 are normalized to a range of
. Since the optical experiments generally have no original image as a reference, the experimental results in
Figure 9 are directly normalized to a range of
.
Then, we also used a head phantom image as the original image. The reconstructed results were acquired from 1% and 2% measurements by using five different approaches: CS, differential compressed sensing (DCS), SCS, “Russian Dolls” CS (RDCS), and our CC method (
Figure 5a,b). It is worth mentioning that here the “Russian Dolls” method is applied to compressive imaging, rather than GI in its original scheme [
30], definitely generating a better image quality. In the simulation, compared with the other existing methods, it only takes a little more (negligible) time for our CC method to iteratively compute the images, but yielding a much better performance. Then, we drew the RE and the peak signal-to-noise ratio (PSNR) of reconstructed images as a function of the sampling ratio. In
Figure 5c,d, it is clearly seen that our CC method is much better than the CS and RD methods with an overwhelming superiority for any sampling ratio. In fact, both RDCS and CC are the sorting method based on the Hadamard basis, and the front patterns with larger piece numbers form the low frequency components of the target, while the image quality will increase when we continuously add the patterns with larger piece numbers. When the sampling ratio is over 50%, the PSNR of RDCS presents a rapid change; it is easy to understand because the Hadamard matrix has a very good structure. According the principle of RDCS, when the sampling ratio exceeds 50%, the patterns with larger piece numbers will be modulated with a higher probability. From the PSNR curve, it can be seen that CC will exceed the DCS and SCS methods when the sampling ratio is over 40%. As mentioned above, SCS has a major drawback that it needs to fully sample the image, and then to pick up the most significant intensities. Our CC method makes up for this defect. It is important to note that, when the sampling ratio is below 40%, it seems that our proposed method shows no advantages to DCS and SCS. That is because the RE and the PSNR, serving as the performance metrics, all quantify the visibility via the calculation of pixel errors. These pixel-wise performance measures may fail to capture the structure of natural images and may cause evaluation misjudgments; i.e., an image which is supposed to have a better visibility may instead have a worse RE or PSNR value. Actually, in
Figure 5a,b, the CC method has a much better visibility than those of other four methods when the sampling ratio is very low, i.e., 1% and 2%, but cannot be characterized very well with the RE or PSNR data of
Figure 5c,d. These examples illustrate the weak correlation of RE and PSNR with perceptual quality under some special cases, and that they sometimes cannot effectively tell the reconstruction quality. The image contrast, brightness and pixel perturbations all will affect the accuracy of PSNR and RE values. Thus, here we introduce another quantitative index mean structural similarity (MSSIM) [
39], which is a full reference metric for evaluating the perceptual difference between two similar images (a reference and a processed image). Unlike RE or PSNR, MSSIM is mainly based on visible structures in the image, with a value range between 0 and 1. The larger is the MSSIM value, the better is the image quality. When
, the processed image is identical to the reference image. The corresponding MSSIM curve is given in
Figure 5e, and the MSSIM values for
Figure 5a,b are also provided. From the MSSIM values, we can see that the MSSIM values of CC are always better than those of other four methods, consistent with the visible results of
Figure 5a,b, while the MSSIM values of RDCS present a ladder rising trend, which keeps in accordance with the theory of RDCS. When the sampling ratio is large enough, the MSSIM values tend to saturate. Therefore, the image quality does not increase indefinitely as the sampling ratio increases.
Generally, there are many noise sources involved in the imaging process, such as illumination fluctuation noise, detector noise, etc. In mathematical expressions, all of them can be finally converted to an additive noise, thus their effects are similar. Here, we focus on the influence of illumination fluctuation noise on the image reconstructions. The spatial light field distribution of noisy illumination source acting on the object is equivalent to the object plus the spatial light field distribution of illumination fluctuation noise [
40]. Here, we calculate the SNR of the illumination light field, which is defined as
, where
denotes the spatial light field of illumination and Std stands for the standard deviation. The properties of MSSIM under different illumination fluctuation noise are presented in
Figure 6, from which we can see that under the same
, our CC method outperforms DCS and SCS, and all of them can suppress a part of noise with the MSSIM value proportional to the
value.
Next, another simulation was made to see the applicability of our method for the object images at large pixel scale. To rule out that CC only works best for images similar to the head phantom, some different gray-scale original objects were chosen from the open access standard test image gallery. Here, images of a man (
Figure 7a), mandrill (
Figure 7g) and peppers (
Figure 7i) were used, all having the same resolution of
pixels. The reconstructions of the man image were performed at the sampling ratio set from 0.78% to 12.50%, with a
stepping increase, as shown in
Figure 7b–f. Since these results were retrieved with the same CC method, it is acceptable to still use the RE and PSNR as the quality evaluation criterion. From the results, we can see that the image quality and the calculation time increase with the sampling ratio. Then, the reconstructions (see
Figure 7h,j) of different object images with a 12.5% sampling ratio aim to simulate the imaging for general scenes. For color-scale cases, we chose our school badge (
Figure 7k) as the object, which was split into the red, green and blue layers. By synthesizing the recovered images of the three wavelength components, the reconstruction of the color image can be obtained, as shown in
Figure 7l. The result shows that a multi-wavelength composite image can be reconstructed clearly with 255 tones with little color distortion. The full-color experiments can be easily performed with three spectral filters to CC sample the red, green, and blue sub-images, and then synthesize the three recovered sub-images to form a color image. The simulations in
Figure 5 and
Figure 7 were all performed with additive white Gaussian noise (its mean is 1% of the measured values mean, and its variance is 1).
Next, we investigated the average performance of our method as a function of image size for a fixed number of different object samples. Here, we picked 12 object samples from the international public standard test image library, and they are airfield, airplane, baboon, barbara, bridge, cablecar, fingerprint, goldhill, man, monarch butterfly, pens, peppers, starfish, and sailboat, respectively, indicated by Obj IDs 1–14. It is known that any natural image has a sparse representation in some basis. As mentioned above, we defined a scalar “sparsity ratio” as the ratio of the number of non-zero (large-value) elements of the image sparse representation coefficients to the total number of image pixels. Since the TVAL3 solver was utilized here, we could use the total variation (TV) operator to sparsely represent the images and calculate the averages of their sparsity ratios at different image sizes. After that, we tested the PSNR performance of our method for different compressive ratios and 12 object samples, compared with RH, DCS, SCS methods. Then, we chose a fixed PSNR value, about 20.334 dB. In this case, we could acquire the lowest required sampling rates of these methods for different image sizes that make the details of the image just be resolved. In
Figure 8, we plot the lowest required sampling ratios of above four methods as a function of image size, each point is obtained by averaging 12 results of different object samples. From the graph, we can also see that the images become sparser with higher pixel resolution because they can be approximated even better by low-frequency components, particularly at higher resolutions. Furthermore, the high-frequency component at a low resolution will eventually become a low-frequency one at higher and higher resolutions for the same image. This is a general rule that we can find when looking at compressed versions of megapixel images. That is why we can acquire smaller sampling ratios for different methods at higher resolutions. However, it can be clearly seen from the curves that our CC approach can reduce the sampling rate to a much lower level than other existing advanced methods when obtaining a fixed imaging quality. It is worth mentioning that, although SCS is a very intuitive technology, it needs to fully sample the image or pre-sample the object and then judge whether the measured value should be stored for each measurement (each logic judgment is actually based on the sampling), and the actual number of measurements is still very high. In short, among these four methods, RH performs the worst, while our CC method wins by a landslide, especially for large-scale images, realizing super sub-Nyquist sampling.
It should be noted that, as long as the computer configuration is high enough, the reconstructed images with much larger pixel size (spatial resolution) can also be achieved. Although high-resolution CS reconstruction can be seen in previous work [
41,
42,
43] by using Kronecker product between arbitrary matrices, structurally random matrix, and Hadamard- and circulant-based sensing matrices, our work provides a new way to further reduce the sampling ratio and offers a new insight into the nature of sampling, also with the same benefits of computational efficiency.
3.2. Experimental Setup and Results
In our experimental setup, as shown in
Figure 9a, the object was illuminated by the collimated and attenuated thermal light beam emitted from a stabilized halogen tungsten lamp, whose wavelength range covers from 360 nm to 2600 nm. Some 2 inch × 2 inch neutral density filters (NDFs) were used to attenuate the light to the ultra-weak light level. The transmission light from the object vertically illuminated a DMD via an imaging lens. The reflected light from the DMD in
direction with respect to the normal incidence input beam was then sampled by a counter-type Hamamatsu H10682-210 photomultiplier tube (PMT). Since the PMT records the total intensity in the form of photon counts, it can be regarded as a single-photon single-pixel (bucket) detector. Our 0.7 inch DMD (ranging from 350 nm to 2700 nm) consisted of
pixels, each of size 13.68
m×13.68
m. The states “on” and “off” of the micromirrors were determined by a preloaded sequence of binary patterns. The onboard storage of the DMDs is loadable for up to 45,000 patterns. We independently developed an improved DMD which enables us to load the pattern sequence onto the DMD in real time, releasing restrictions on the onboard memory of the DMD. Here, we used the CC sequence to generate our DMD modulated basis patterns.
The elements of the Hadamard matrix
A take values of 1 or
, while the binary patterns encoded on the DMD consist of the values of 1 or 0, which cannot ensure a good image quality with respect to the RIP. It was found that by subtle shifting and stretching operations the matrix
A can be divided into two complementary matrices
and
, where 1 stands for an array consisting all ones [
44]. Hence, the Hadamard matrix in our optimal ordering can be modulated on the DMD by displaying each complementary basis pattern pair: one pattern shaped from
immediately followed by its complementary pattern shaped from
, i.e., the micromirror states “on” and “off” are reversed. Then, the value range of the differential patterns
will become either 1 or
, actually realizing “positive–negative” intensity modulation as well as differential measurements with a mean
. This method is also named complementary or differential compressed sensing [
19].
For simplicity, we tested our system with a gray-scale object. Here, we chose a negative 1951 USAF resolution test chart as the original object (see
Figure 9b), whose black parts block the light and white parts transmit the light. The 1951 USAF resolution test chart consists of a series of stripes decreasing in size, while the standard target element is composed of two sets of lines, each set being made up of three lines separated by spaces of equal width. Suppose
r is the number of lines per mm, the parallel lines are
mm long and
mm wide with space
mm wide between the parallel lines. The space between the vertical and horizontal lines is
mm wide. The elements within a group are numbered from 1 to 6, which are progressively smaller. The group number covers from
to 7. The length of any target element line can be expressed as
mm, while the width equals the length divided by 5, also is equivalent to
Resolution (line pair/mm). In
Figure 9b, the red square is the object image projected on the central square region of our DMD, covering
pixels (micromirrors). Note that the red square is in Group
; it is easy to compute the width of each line in the red square (all in Group
), i.e., 793.70
m for Element 3, 707.11
m for Element 4, and 629.96
m for Element 5.
In our experiments, we first used a CC sequence of
-pixel Hadamard basis patterns, where each pixel unit of the pattern comprises
adjacent micromirrors. By utilizing our strategy, a coarse image of the object with a low-resolution of
pixels was retrieved from 1024 patterns, i.e., with a sampling rate of 25%, as shown in
Figure 9c. Then, by using a NDF of transmissivity 0.001,
Figure 9(d1–d10) illustrates the reconstructed images of
pixels by using a series of sampling ratios with a coverage from 0.2% to 100%, where the piece numbers are in their ascending order. From the results, we can see that the lowest sampling ratio in our experiments is about 0.2%, i.e., 524 measurements for
pixels. For some sparser objects, all the sampling rates can be lower. However, among these approaches, our method provides a shortcut to make the minimum number of measurements, considering the actual sparsity ratio of the object, much better than the cases of random measurements, as shown in
Figure 9(f1–f7). It is known that the DMD is the fastest spatial light modulator for the time being, and the nominal maximal binary pattern switching rates of the commercially available DMDs reach 32,550 Hz (patterns/s). With such super sub-Nyquist sampling ratio (0.2% for example), it is available for
frames per second (fps) at
pixel resolution,
fps at
pixels, and
fps at
pixels (regular pixel dimension of the DMD), incorporating two adjacent complementary patterns for differential measurements. Such frame rate is more than enough for real-time applications. In our experiments, we set the modulation frequency to 20 kHz, the acquisition time of the
-pixel image with 0.2% sampling ratio only takes 0.052 s, and the averaged computation time takes about 100 s. If a supercomputer with parallel processing is used or a system hardware is realized, the computation time will be much shorter, in order of milliseconds. In many scenarios, the measurement time is more demanding than the reconstruction time. Therefore, we have reasons to believe that our method can be applied to replace many commercial cameras such as mobile phone cameras in the near future.
Figure 9(e1–e4) shows some comparative examples of using the descending order of piece numbers with a sampling ratio changing from 0.78% to 50%. All their performances are poor, consistent with the simulation results in
Figure 2f. The reason is that the patterns with the largest number of connected regions often play the least significant roles. Imagine the connected regions are infinitely subdivided, the most extreme case is that the size of each connected regions is one pixel. Use of such kind of pattern to cover or to modulate the object, the measured value tends to be an average with some negligible fluctuations. However, according to the theory of linear programming, the measured values should have some significant fluctuations around the mean. In contrast, when the patterns tend to be lumped, the corresponding measured values will be larger than the average value with a higher probability, i.e., the correlation between these patterns and the target image is higher. Thereby, the smaller is the number of connected domains of one pattern, the more significant is the contribution of this patterns to the image reconstruction.
Now, let us recall the multiscale/pyramid methods used for image representation, such as wavelet transforms. A Hadamard basis pattern with a smaller number of connected regions (or pieces) actually captures low frequency characteristics of the object image, which is essential for a rough but representative reconstruction, while those patterns with larger piece numbers will undoubtedly add the details of high frequency components by choosing the cutoff sampling percentage if the measurement budget allows. This theory can also explain how our method works.
For performance comparison, we also present the reconstructed images using RH sensing matrix, with the sampling ratios changing from 1.56% to 100.00% with a
stepping increase, as shown in
Figure 9(f1–f7). From the results, we can see that the image qualities of RH approach with the same sampling ratios are much worse than those of our method. Since neither CS nor DCS can recover any image at such low sampling ratios, SCS requires full sampling, and RDCS cannot generate RD sequence at such high pixel resolution, so their experimental results are not presented here.
Since the SPI has distinct advantages in ultra-weak light noisy measurement environment, we also tested the performance of our CC method in this case, providing the reconstructed results under different SNRs (see
Figure 9(g1–g4)) with a same sampling ratio of 3.125%. They were performed by applying four different NDFs, whose transmissivity is 0.001, 0.0025, 0.005 and 0.01 (from left to right), respectively. In these experiments, there was no obstacle placed in the light path to block the light. From the results, we can conclude that our approach is applicable to high (even higher) SNR scenarios. The image quality decreases as the transmissivity of NDFs increases, because the more the light is transmitted, the larger the stray light reflected from the metal surface of the DMD will be.
In view of the fact that the SPI only requires using a single-pixel detector to collect the total light intensity to complete the task of array detection, it has an inherent advantage of being able to resist turbulence. Although the turbulence has a great impact on the spatial light field distribution, it only plays a role of attenuating the total light intensity. To test the performance of our CC approach under turbulence condition, we placed some pieces of lens cleaning tissues (some kind of organic fiber and can be treated as the turbulent obstacle here) between the object and the PMT, as shown in
Figure 9a. The number of tissues was increased from one to three and the results are presented in
Figure 9(h1–h3), also with a sampling ratio of 3.125%. Some part of the light reflected from the DMD passes through the tissues, and is partly scattered. Thus, the light collected by the PMT is a mixture of the direct light and the indirect light. Despite the detector being completely obscured, our system still retrieved the object through the turbulent obstacles. Thus, the results demonstrate the potential of our system for revealing objects obscured behind obstacles (e.g., foliage) or other scattering materials in actual scenarios.