A Method for Analyzing the Impact of Intra-System and Inter-System Interference on DME Based on Queueing Theory
Abstract
:1. Introduction
2. Overview of DME and JTIDS
2.1. First Principles and Baseband Signal of DME
2.2. First Principles and Baseband Signal of JTIDS
2.3. Frequency Distribution of DME and JTIDS
3. Analysis Method of iNterference on DME
3.1. Metric of Interference on DME
3.2. Calculation for P(I)
3.2.1. Calculation for
3.2.2. Calculation for
- When n is small: Since PRF and duty cycle of DME interrogation are all small, the collision probability of interrogations is small accordingly. It can be assumed that dead time is a part of pulse duration, thus, the desired pulse duration equals plus . All the interrogations are assumed to be independently at the same time, according to [10], the probability of DME interrogations not interfered in search mode is given as follows:Similarly, the probability of DME interrogations not interfered in track mode is given as follows:Combining Equations (5)–(7), the average probability of multi-path DME interrogations not interfered can be obtained as follows:Event M and event J are assumed to be statistically independent, that is to say, inter-system and intra-system interference are independent of each other. Substituting Equations (4) and (8) into (3), we obtainThe collision probability between two or more DME interrogations will increase when n is large. The result based on Equation (7) is smaller than actual value. Moreover, intra-system interference is correlative with inter-system interference, the error using Equation (9) is large if n is large. Equation (9) can be apply to a small quantity of aircraft only.
- When n is large: We can adopt simplifying assumption that these interrogations are randomly distributed with respect to time forming a Poisson process [5], considering that interrogations will be abandoned if its arrival time overlaps with dead time generated by front interrogation, and hence the receiving process of DME interrogations can be regarded as a quasi M/D/1/0 theory model. In such a birth-and-death model M/D/1/0, the interrogation pulses are customers, transponder is service facility, “M” represents that the arrivals occur from an infinite source in accordance with a Poisson process with parameter defined in Figure 4—that is, the inter-arrival times are independent exponential with mean 1/, “D” represents service times that are deterministic and equivalent to dead time plus , “1” represents single server, and “0” means that customer will depart when its arrival time overlaps with service time [16]. Service rate is given as follows:According to [11], the probability of customers serviced Q can be calculated as follows:where the density of interrogation pulse-stream is subject to , Q is condition probability. The subsequent customer cannot affect the front service in a normal M/D/1/0 theory model; however, if the subsequent interrogation pulse overlaps with the front interrogation pulse before it enters into a transponder, the front interrogation pulse will be abandoned too, which is different from a normal birth-and-death model. Considering the interrogation duration on its back side, the probability of an interrogation not overlapped with its subsequent interrogations is calculated to be . With the help of queueing theory model, can be calculated as follows:Substituting Equations (4) and (12) into (3) gives:
3.3. Calculation for P(D)
3.4. Calculation for P(R)
4. Results and Discussion
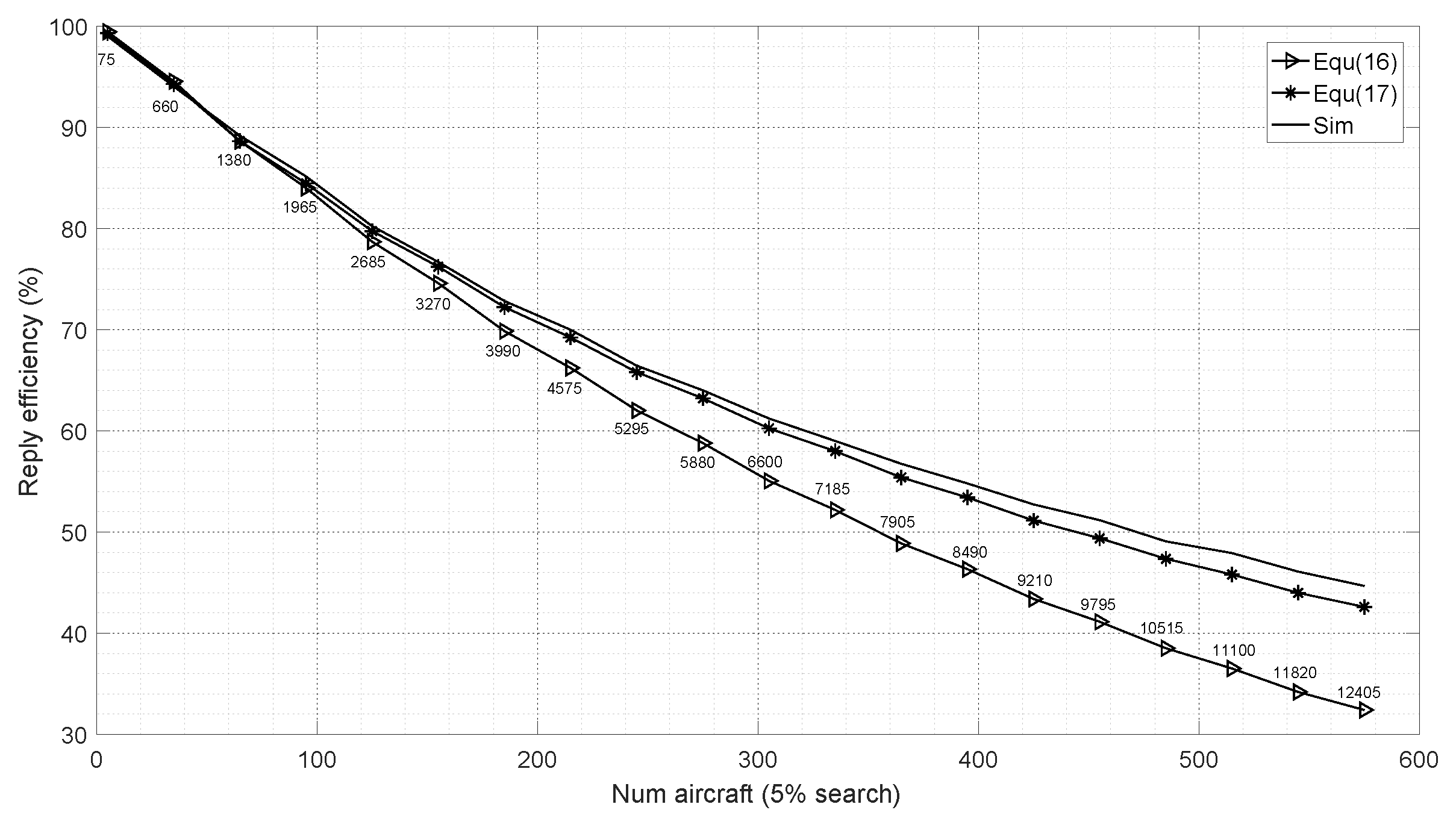
4.1. The Result of Re Based on Different Methods
- , .
- 95% of aircraft are in track mode and others are in search mode.
- DME operates in mode X, s and s.
- PRF of identification pulse: .
- Inter-system interference is absent.
- Simulation time: 1 s.
- Number of aircraft: variation from 5 to 600 every 3.
- Number of Monte Carlo simulation: 1000.
4.2. Analysis of JTIDS Interference and DME Mode on RE
- When DME operates in mode Y, s, s and s.
- JTIDS signal duration: ms.
- Number of aircraft: variation from 5 to 400 every 15.
- means that there is no JTIDS interference, means that JTIDS is in present.
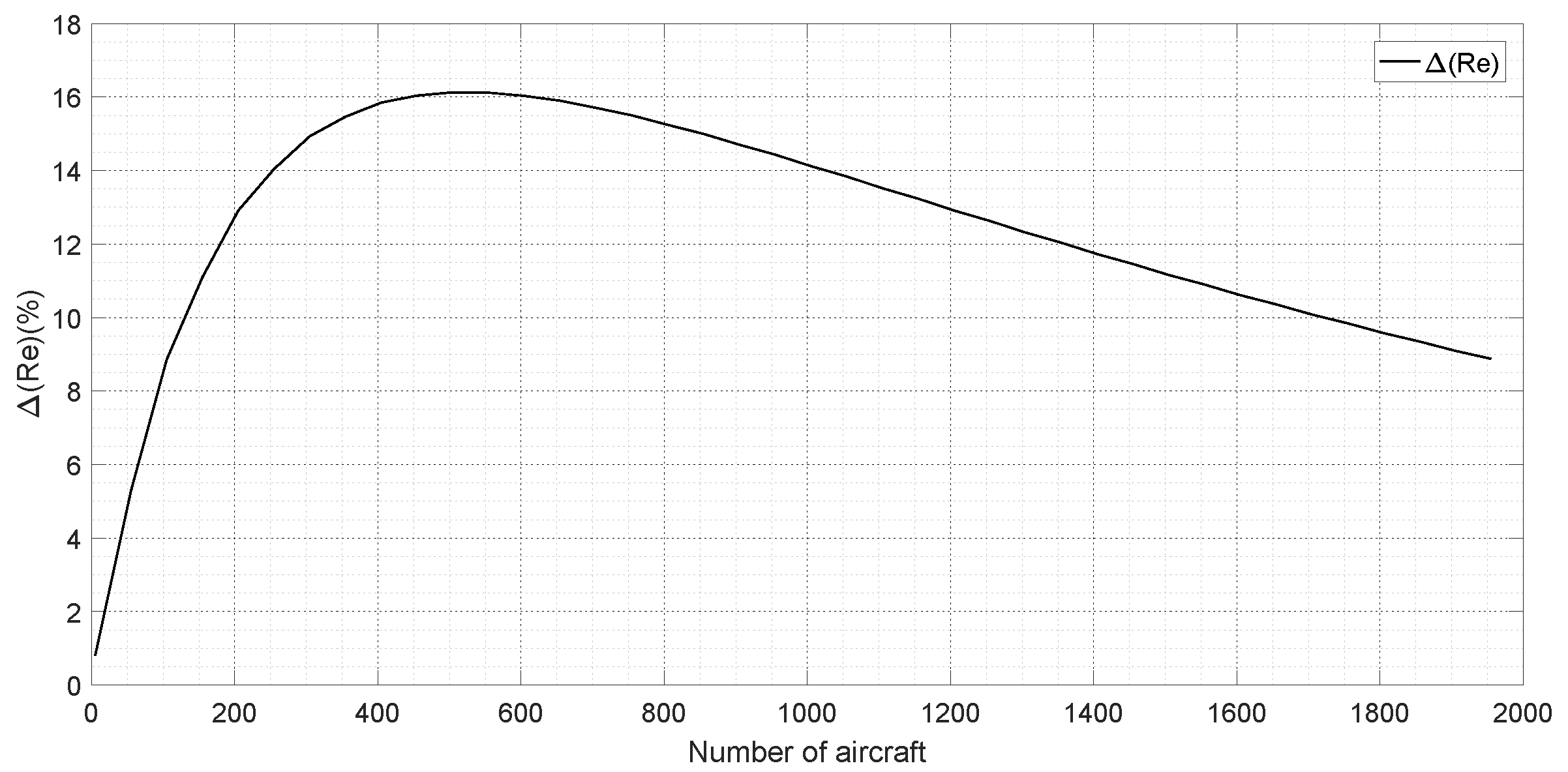
4.3. Impact of Reply Rate and RE on DME Capacity
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DME | Distance Measuring Equipment |
| JTIDS | Joint Tactical Information Distribution System |
| RE | Reply Efficiency |
| ICAO | International Civil Aviation Organization |
| ACSS | Airborne Collision Avoidance System |
| IFF | Identification Friend or Foe |
| ATCRBS | Air Traffic Control Radar Beacon System |
| EMC | Electromagnetic Compatibility |
| SNR | signal to noise ratio |
| BER | Bit Error Rate |
| PRF | Pulse Repetition Frequency |
| PPCM | Periodic Pulse Collision Method |
References
- ICAO. Aeronautical Telecommunications, 6th ed.; ICAO: Montreal, QC, Canada, 2006. [Google Scholar]
- Ulrich, E.; Michael, S. Overview of legacy systems in L-band and its influence on the future aeronautical communication system LDACS1. IEEE Aerosp. Electron. Syst. Mag. 2014, 29, 31–37. [Google Scholar] [CrossRef]
- Najett, N.; De Lacerda, R.; Azoulay, A.; Letertre, T.; Outtier, O. Cosite Coexistence between Future L-DACS2 and Legacy DME Systems. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2585–2600. [Google Scholar]
- Neji, N.; De Lacerda, R.; Azoulay, A.; Letertre, T.; Outtier, O. Survey on the Future Aeronautical Communication System and Its Development for Continental Communications. IEEE Trans. Veh. Technol. 2013, 62, 182–191. [Google Scholar] [CrossRef] [Green Version]
- Houdzoumis, V.A. A Simplified Method for the Analysis of Interference from JTIDS Radio Networks to DME Aeronautical Radionavigation Systems. J. Navig. 2009, 62, 721–737. [Google Scholar] [CrossRef]
- Wolff, A.M.; Akos, D.M.; Lo, S. Potential radio frequency interference with the GPS L5 band for radio occultation measurements. Atmos. Meas. Tech. 2014, 7, 3801–3811. [Google Scholar] [CrossRef] [Green Version]
- Baek, H.; Lim, J. Spectrum Sharing for Coexistence of Fixed Satellite Services and Frequency Hopping Tactical Data Link. IEEE J. Sel. Areas Commun. 2016, 34, 2642–2649. [Google Scholar] [CrossRef]
- Tsinos, C.G.; Foukalas, F.; Tsiftsis, T.A. Resource Allocation for Licensed/Unlicensed Carrier Aggregation MIMO Systems. IEEE Trans. Commun. 2017, 65, 3765–3779. [Google Scholar] [CrossRef] [Green Version]
- Steingass, A.; Thiasiriphet, T.; Samson, J. Modeling Distance Measurement Equipment (DME) Signals Interfering an Airborne GNSS Receiver. Navigation 2018, 65, 221–230. [Google Scholar] [CrossRef]
- Lo, S.C.; Enge, P. Assessing the Capability of Distance Measuring Equipment to Support Future Air Traffic Capacity. Navig. J. Inst. Navig. 2012, 59, 249–261. [Google Scholar] [CrossRef]
- Zhang, J.; Han, G.; Qian, Y. Queuing Theory Based Co-Channel Interference Analysis Approach for High-Density Wireless Local Area Networks. Sensors 2016, 16, 1348. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, Y.; Zhu, J.; Jiang, X.; Tokuda, H. On the Throughput Capacity Study for Aloha Mobile Ad Hoc Networks. IEEE Trans. Commun. 2016, 64, 1646–1659. [Google Scholar] [CrossRef]
- Franceschetti, M.; Dousse, O.; Tse, D.N.C.; Thiran, P. Closing the Gap in the Capacity of Wireless Networks Via Percolation Theory. IEEE Trans. Inf. Theory 2007, 53, 1009–1018. [Google Scholar] [CrossRef] [Green Version]
- Systems, N.G.M. Understanding Link16: A Guidebook for United States Navy and United States Marines Corps Operators, 3rd ed.; Link 16 In Service Engineering Agency: Carlsbad, CA, USA, 2004. [Google Scholar]
- Mei, W.; Cai, S. JTIDS/LINK16 Data Link, 1st ed.; National Defense Industry Press: Beijing, China, 2007.
- Daigle, J.N. Queueing Theory with Applications to Packet Telecommunication; Springer: Berlin, Germany, 2005. [Google Scholar]

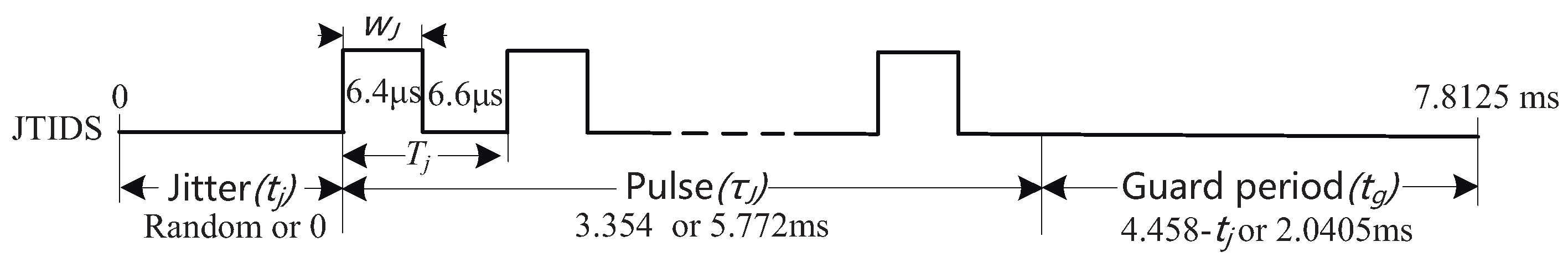
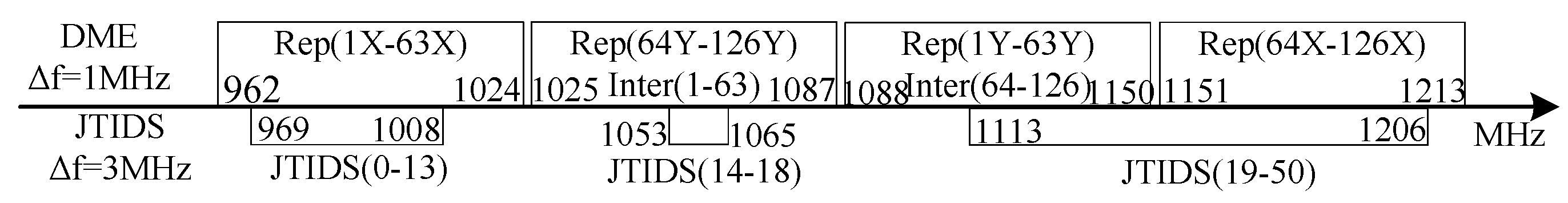


| Signal Type | Operation Mode | Pulse Duration (s) | Pulse Interval (s) | Signal Duration (s) | PRF(Hz) | |
|---|---|---|---|---|---|---|
| Tracking | Searching | |||||
| Interrogation | X | 3.5 | 12 | 15.5 | 10–30 | 40–150 |
| Y | 36 | 39.5 | ||||
| Reply | X | 12 | 15.5 | 700–2700 | ||
| Y | 30 | 33.5 | ||||
| Reply Rate (ppps) | JTIDS | Mode | Number of Aircraft | |
|---|---|---|---|---|
| 2700 | Yes | X | 71.4% | 159 |
| Y | 52.5% | 216 | ||
| No | X | 75.3% | 154 | |
| Y | 55.3% | 210 | ||
| 2848 | Yes | X | 70% | 171 |
| 1748 | Y | 100 | ||
| 3214 | No | X | 200 | |
| 1964 | No | Y | 117 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, G.; Fan, Y. A Method for Analyzing the Impact of Intra-System and Inter-System Interference on DME Based on Queueing Theory. Sensors 2019, 19, 348. https://doi.org/10.3390/s19020348
Jiang G, Fan Y. A Method for Analyzing the Impact of Intra-System and Inter-System Interference on DME Based on Queueing Theory. Sensors. 2019; 19(2):348. https://doi.org/10.3390/s19020348
Chicago/Turabian StyleJiang, Guofeng, and Yangyu Fan. 2019. "A Method for Analyzing the Impact of Intra-System and Inter-System Interference on DME Based on Queueing Theory" Sensors 19, no. 2: 348. https://doi.org/10.3390/s19020348
APA StyleJiang, G., & Fan, Y. (2019). A Method for Analyzing the Impact of Intra-System and Inter-System Interference on DME Based on Queueing Theory. Sensors, 19(2), 348. https://doi.org/10.3390/s19020348




