Study on Dynamic Monitoring of Wire Rope Tension Based on the Particle Damping Sensor
Abstract
:1. Introduction
2. Real-Time Monitoring System for Wire Rope Tension of Multi-Rope Friction Hoist
3. Sensor Design
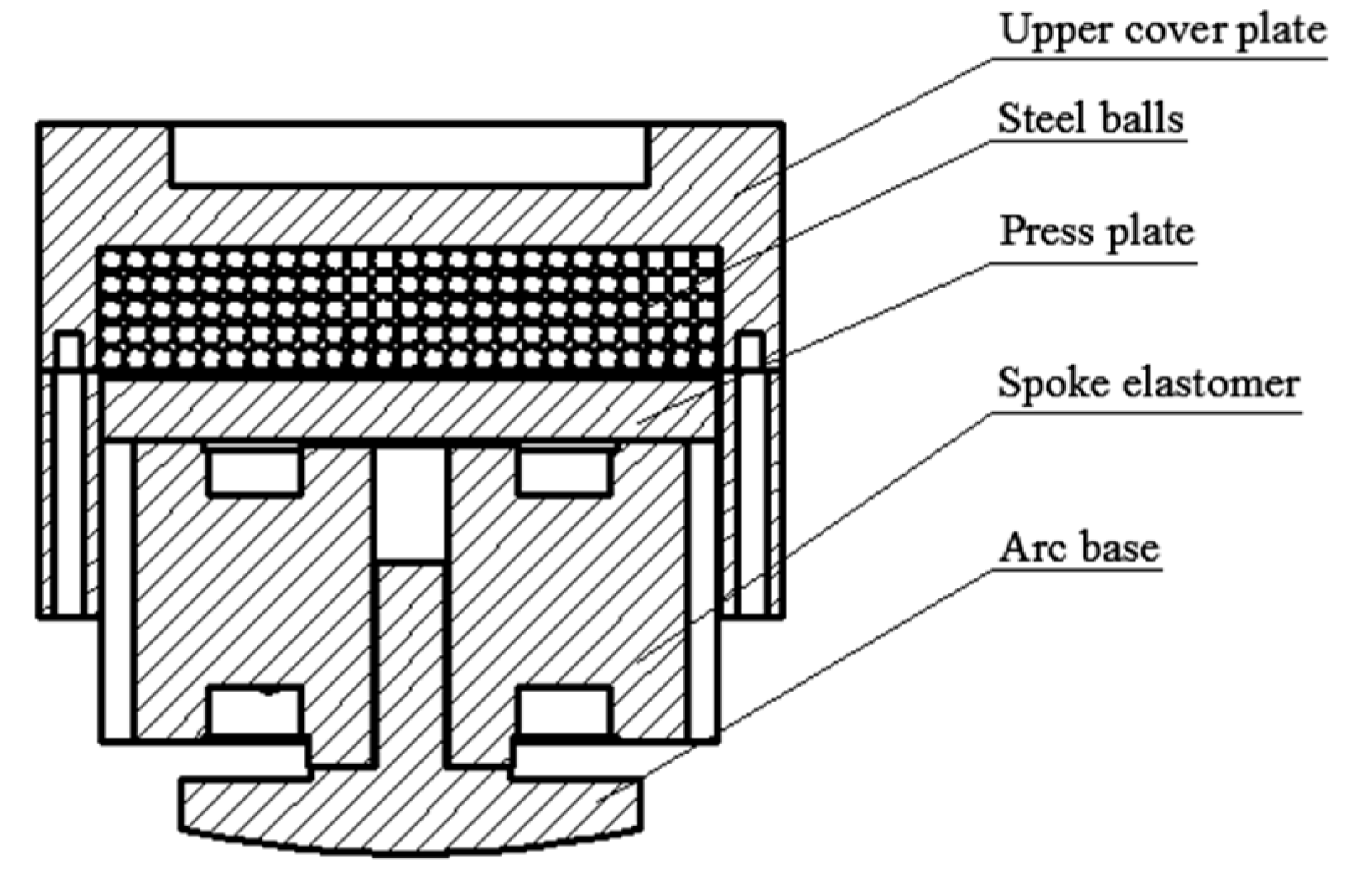
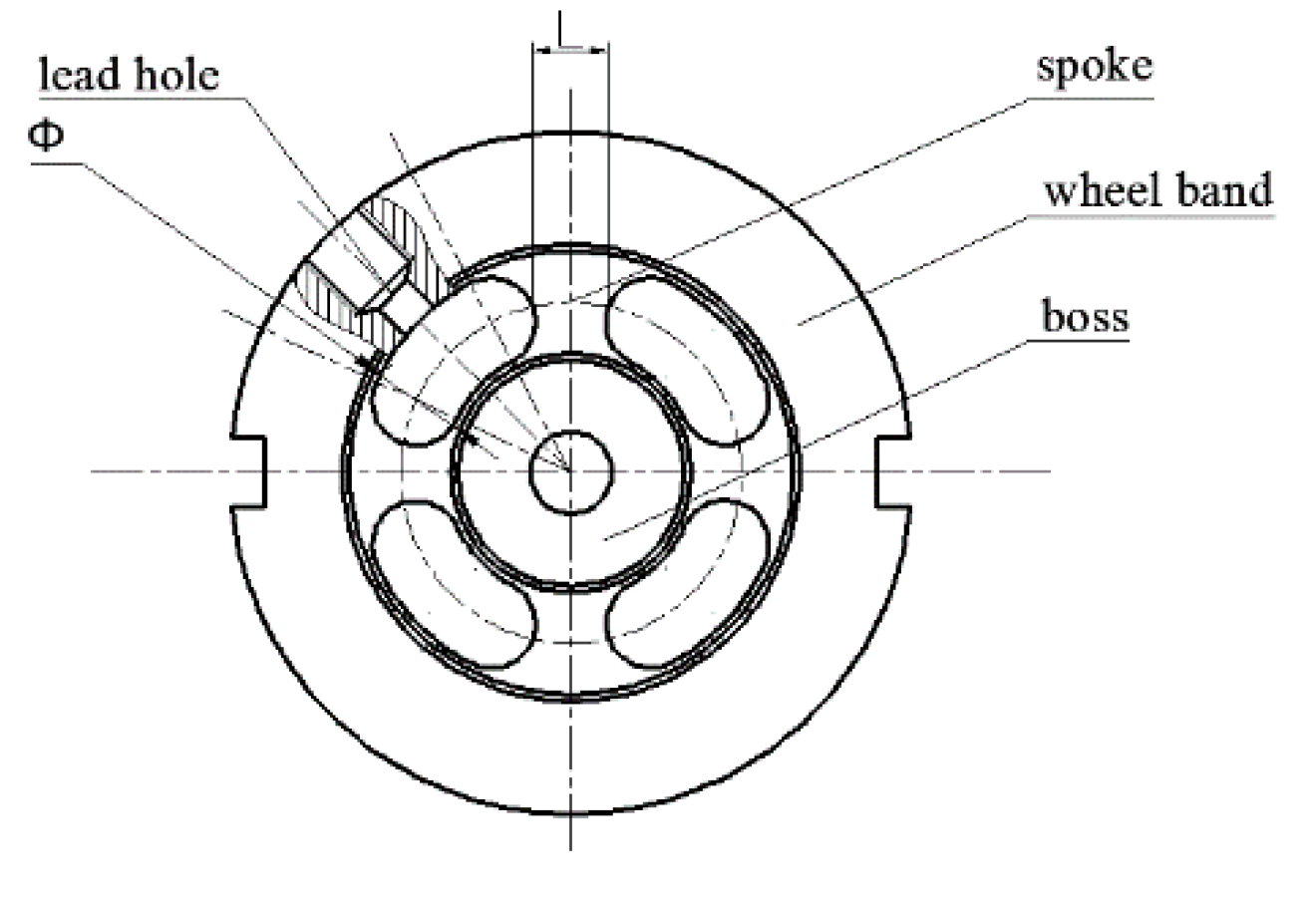
3.1. Structure of Particle Damping Sensor
3.2. Measurement Principle of Particle Damping Sensor
3.3. Simplified Mechanical Model for Vibration Attenuation and Energy Dissipation of Particle Damping Sensor
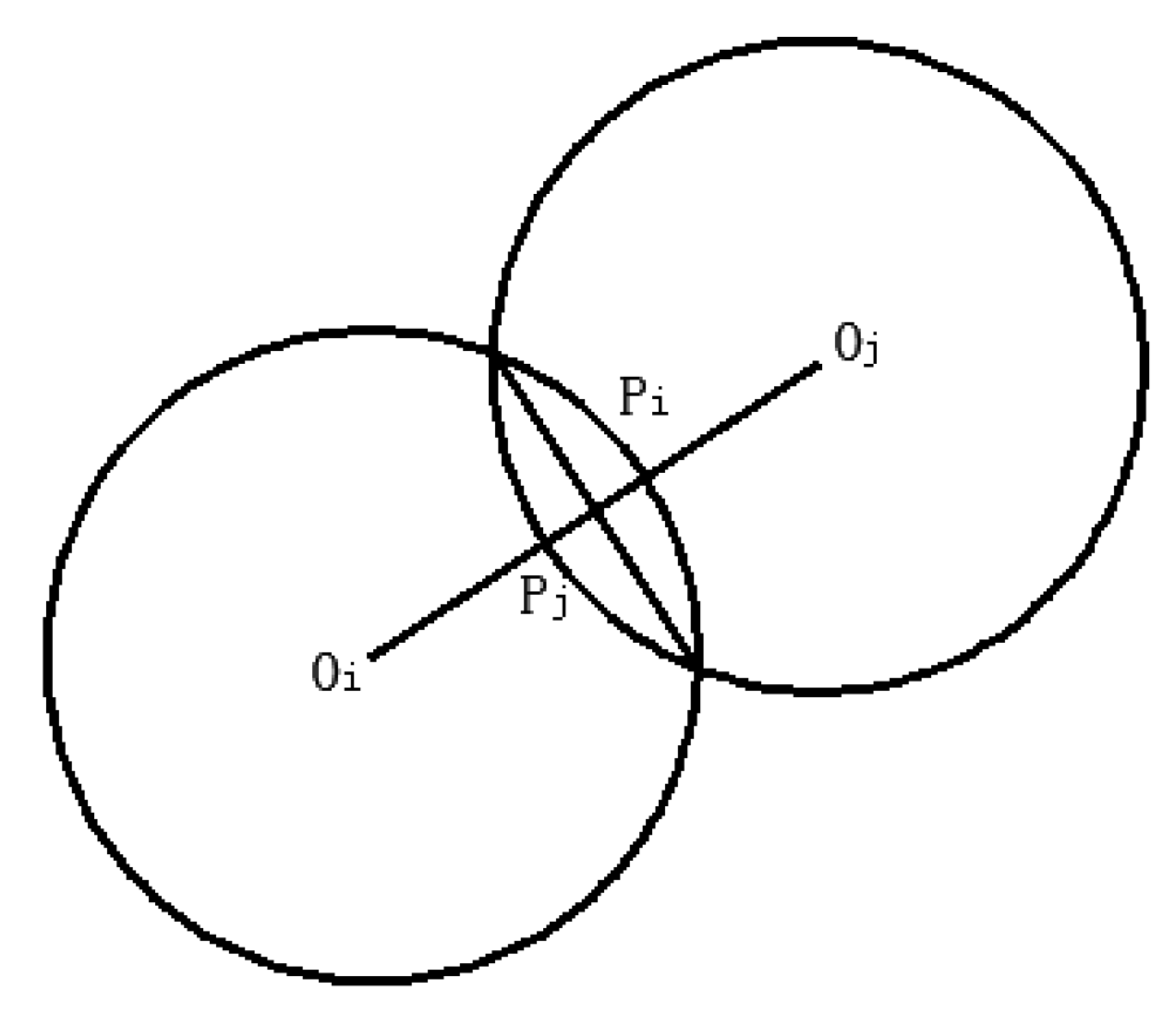
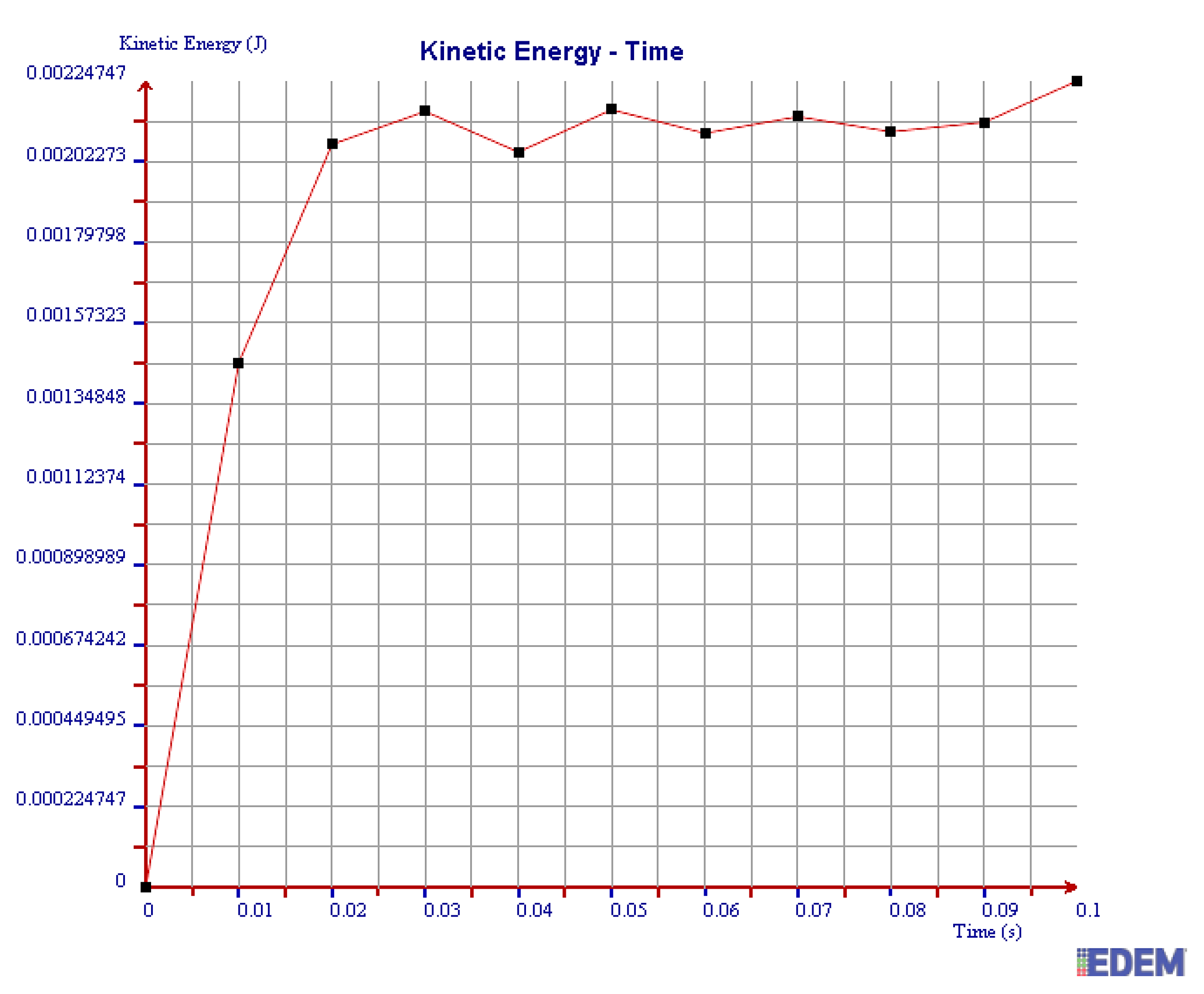
3.4. Particle Damping Model and the Energy Dissipation Principle Based on DEM
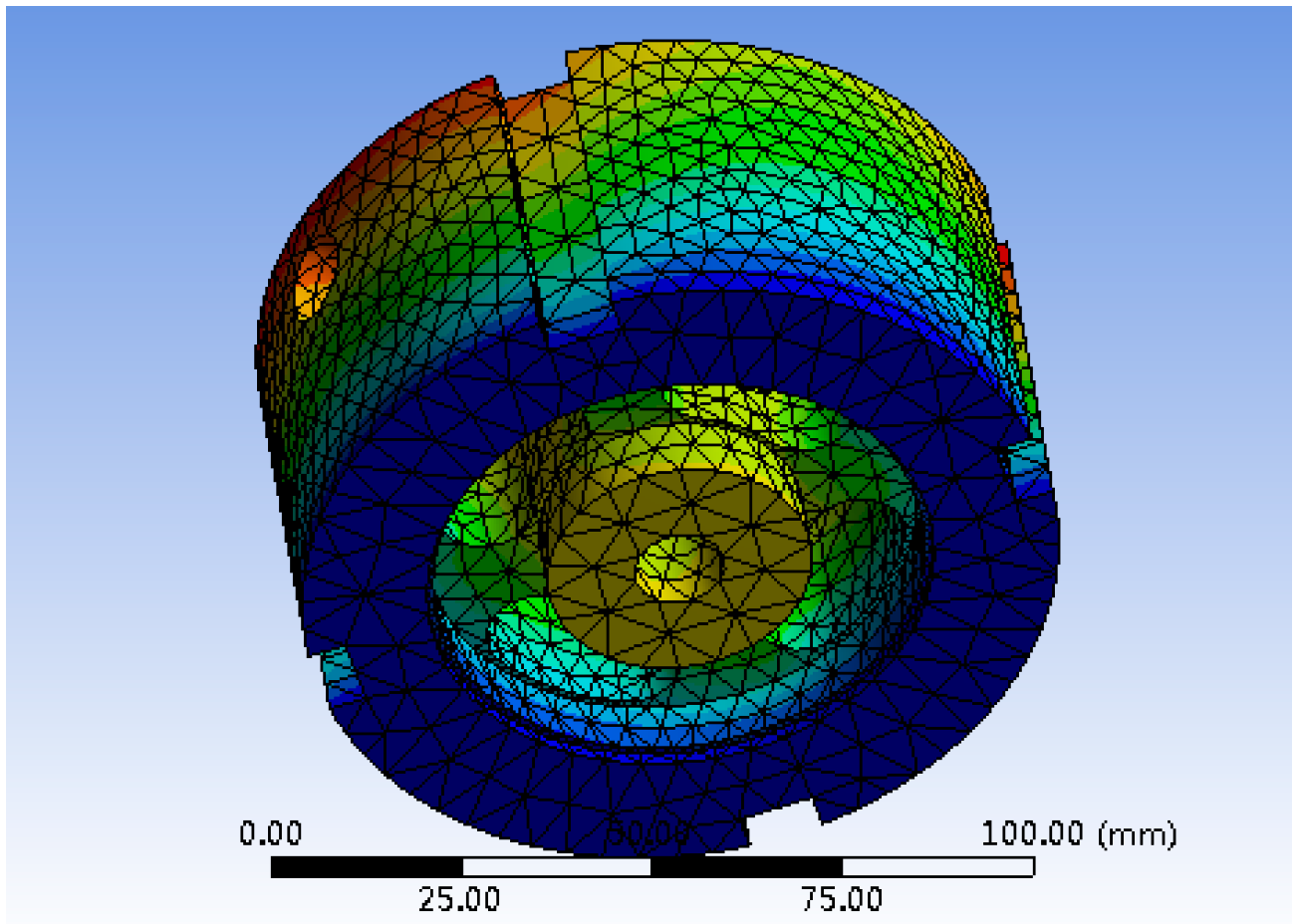
4. Simulation Analysis of the Sensor
4.1. Simulation of Vibration Reduction and Filtering Effect Based on Particle Damping Parameters
4.1.1. Effect of Particle Diameter on Damping Effect
4.1.2. Influence of Particle Materials on Damping Effect
5. Calibration and Field Test of the Sensor
5.1. Static Calibration of the Sensor
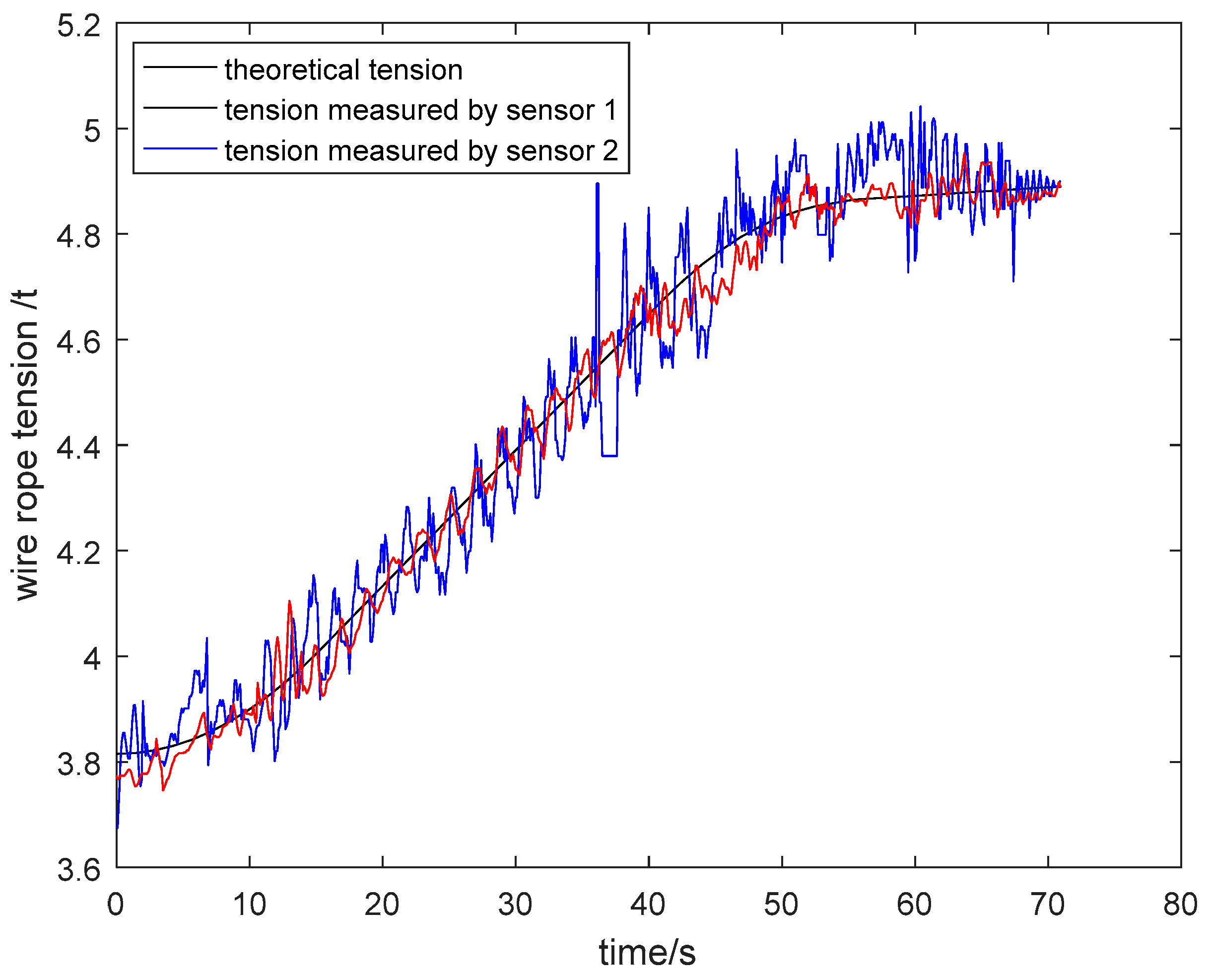
5.2. Field Application of the Sensor
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Tan, L. Design of hoisting load monitoring device of mine. Ind. Mine Autom. 2010, 36, 81–83. [Google Scholar]
- Lu, S.B.; Zhang, G.K. Design and implementation of monitoring instrument for tension of wire rope used for mine hoist based on LabWindows/CVI. Comput. Meas. Control 2015, 23, 2924–2927. [Google Scholar]
- Shi, T.J.; Wang, P.; Wang, B. Design of wirerope tension monitoring system of mine hoist. Ind. Mine Autom. 2014, 40, 103–105. [Google Scholar]
- Hecker, G.F.K.; Kroonstuiver, J. The Safe Use of Mine Winding Ropes, Volume 6: Studies towards a Code of Practice for the Performance, Operation, Testing and Maintenance of Drub Winders; Safety in Mines Research Advisory Committee: Auckland, New Zealand, 1996; pp. 1–135. [Google Scholar]
- Beus, M.J.; Mccoy, W.G. Mine shaft conveyance load-monitoring system. In Proceedings of the IEEE/Industrial Application Society Conference, Orlando, FL, USA, 8–12 October 1995. [Google Scholar]
- Wang, Z.C.; Nie, Z.F.; Shao, H.Y. Dynamic tension test of wire-rope of multiple rope friction winder. Chin. J. Sci. Instrum. 2004, 25, 402–405. [Google Scholar]
- Zhang, X.G.; Song, Z.Y.; Da, J.P.; Fu, J.B. A Novel Acoustic Filtering Sensor for Real-Time Tension Monitoring of Hoist Wire Ropes. Sensors 2018, 18, 2864. [Google Scholar] [CrossRef] [PubMed]
- Deng, D.G.; Wu, X.J.; Zuo, S. A Steel Wire Stress Measuring Sensor Based on the Static Magnetization by Permanent Magnets. Sensors 2016, 16, 1650. [Google Scholar] [CrossRef]
- Xu, J.J.; Yang, W.; Zhang, L.Y.; Han, R.S.; Shao, X.T. Multi-Sensor Detection with Particle Swarm Optimization for Time-Frequency Coded Cooperative WSNs Based on MC-CDMA for Underground Coal Mines. Sensors 2015, 15, 21134–21152. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.W.; Li, J.H.; Li, Y.Y.; Chen, Y.L.; Xu, L.X. Design and Fabrication of a Miniaturized GMI Magnetic Sensor Based on Amorphous Wire by MEMS Technology. Sensors 2018, 18, 732. [Google Scholar] [CrossRef]
- Wang, D.T.; Li, H.W.; Wang, G.H.; Xu, C.H.; Meng, X.R.; Zhang, H.G. Design of fiber grating sensor for steel wire rope tension measurement of mine hoist. Ind. Mine Autom. 2018, 44, 106–110. [Google Scholar]
- Lu, Z.; Wang, D.C.; Li, P.Z. Comparison study of vibration control effects between suspended tuned mass damper and particle damper. Shock Vib. 2014, 3, 1–7. [Google Scholar] [CrossRef]
- Wang, M. Feasibility study of nonlinear tuned mass damper for machining chatter suppression. J. Sound Vib. 2011, 330, 1917–1930. [Google Scholar] [CrossRef]
- Lu, Z.; Lu, X.L.; Yan, W.M. Experimental investigation into the vibration control effects of particle damper. China Civ. Eng. J. 2012, 45, 243–247. [Google Scholar]
- Park, W.H. Mass-Spring-Damper Response to Repetitive Impact. J. Eng. Ind. 1967, 89, 587–596. [Google Scholar] [CrossRef]
- Skipor, E.; Bain, L.J. Application of Impact Damping to Rotary Printing Equipment. J. Mech. Des. 1980, 102, 338–343. [Google Scholar] [CrossRef]
- Sims, N.D.; Amarasinghe, A.; Ridgway, K. Particle Dampers for Workpiece Chatter Mitigation. In Proceedings of the International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005. [Google Scholar]
- Aiba, T.; Murata, R.; Henmi, N.; Nakamura, Y. An Investigation on Variable-Attractive-Force Impact Damper and Application for Controlling Cutting Vibration in Milling Process. J. Jpn. Soc. Precis. Eng. 1995, 61, 75–79. [Google Scholar] [CrossRef]
- Shah, B.M.; Pillet, D.; Bai, X.M.; Keer, L.M. Construction and Characterization of a Particle-Based Thrust Damping system. J. Sound Vib. 2009, 326, 489–502. [Google Scholar] [CrossRef]
- Guo, Y.Y.; Yang, Q.L.; Hu, L.; Sun, L. Experimental Investigation of Damping Properties of the Particle Dampers with Piston. Bull. Sci. Technol. 2016, 32, 12–16. [Google Scholar]
- Zhang, H.D.; Hong, Y.M.; Du, J. Impact Test on the Granular Damper. Ordnance Ind. Autom. 2016, 35, 8–11. [Google Scholar]
- Liu, B.; Wang, Y.R.; Tang, W.; Feng, H.H. Design methodology for particle dampers applied to a wheel structure. J. Aerosp. Power 2014, 29, 2476–2485. [Google Scholar]
- Zhu, Y.; Zhou, B.W.; Gu, R.; Jiang, L. Design of the Sensor Used for the Measure of Cut Load. Mach. Des. Manuf. Eng. 2002, 31, 87–89. [Google Scholar]
- Chi, X.Z.; Jin, H.Z.; Wang, J.S. Research on Piezoresistive Complexed Inertial Accelerometer. Chin. J. Sci. Instrum. 2003, 24, 262–271. [Google Scholar]









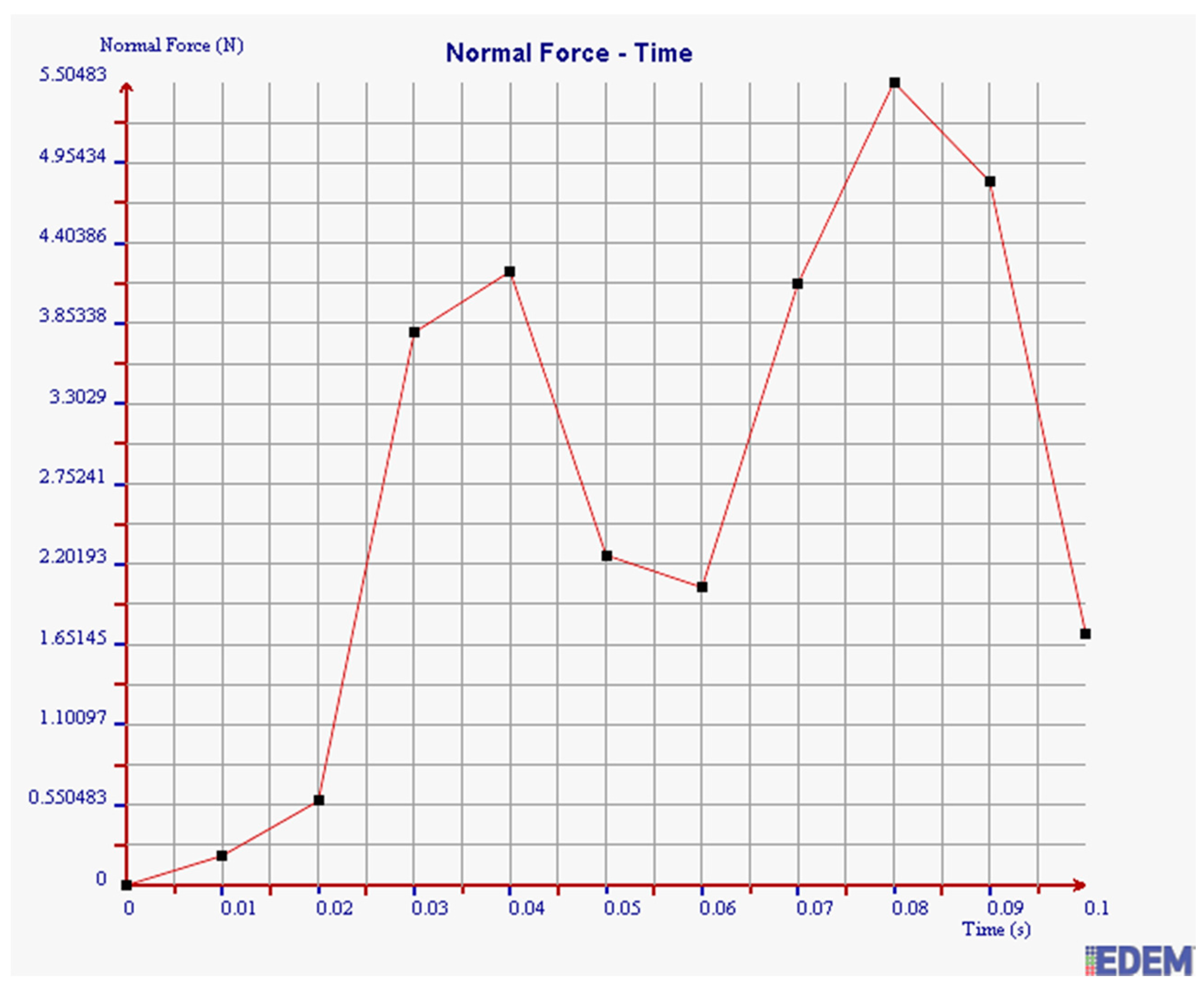
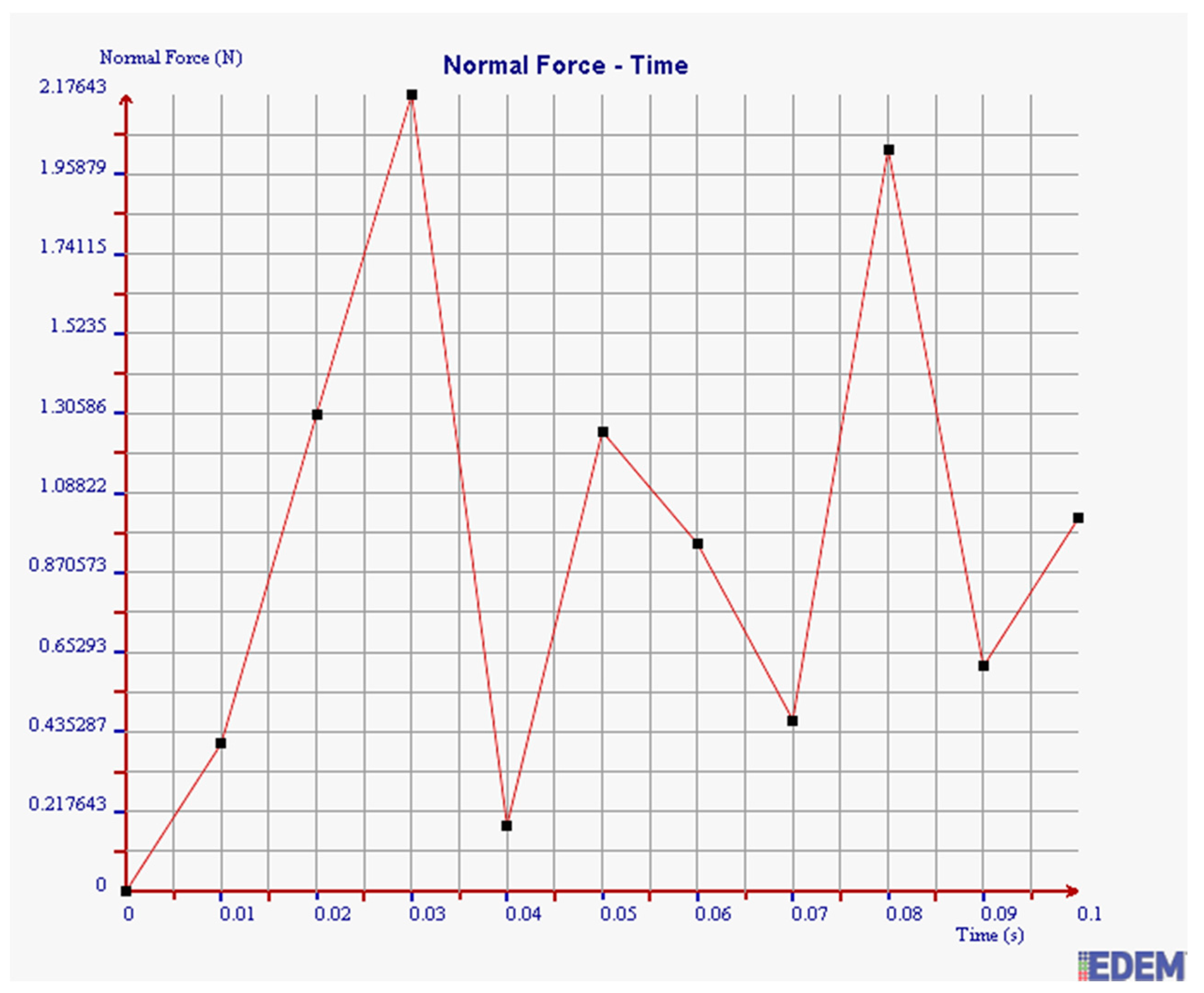

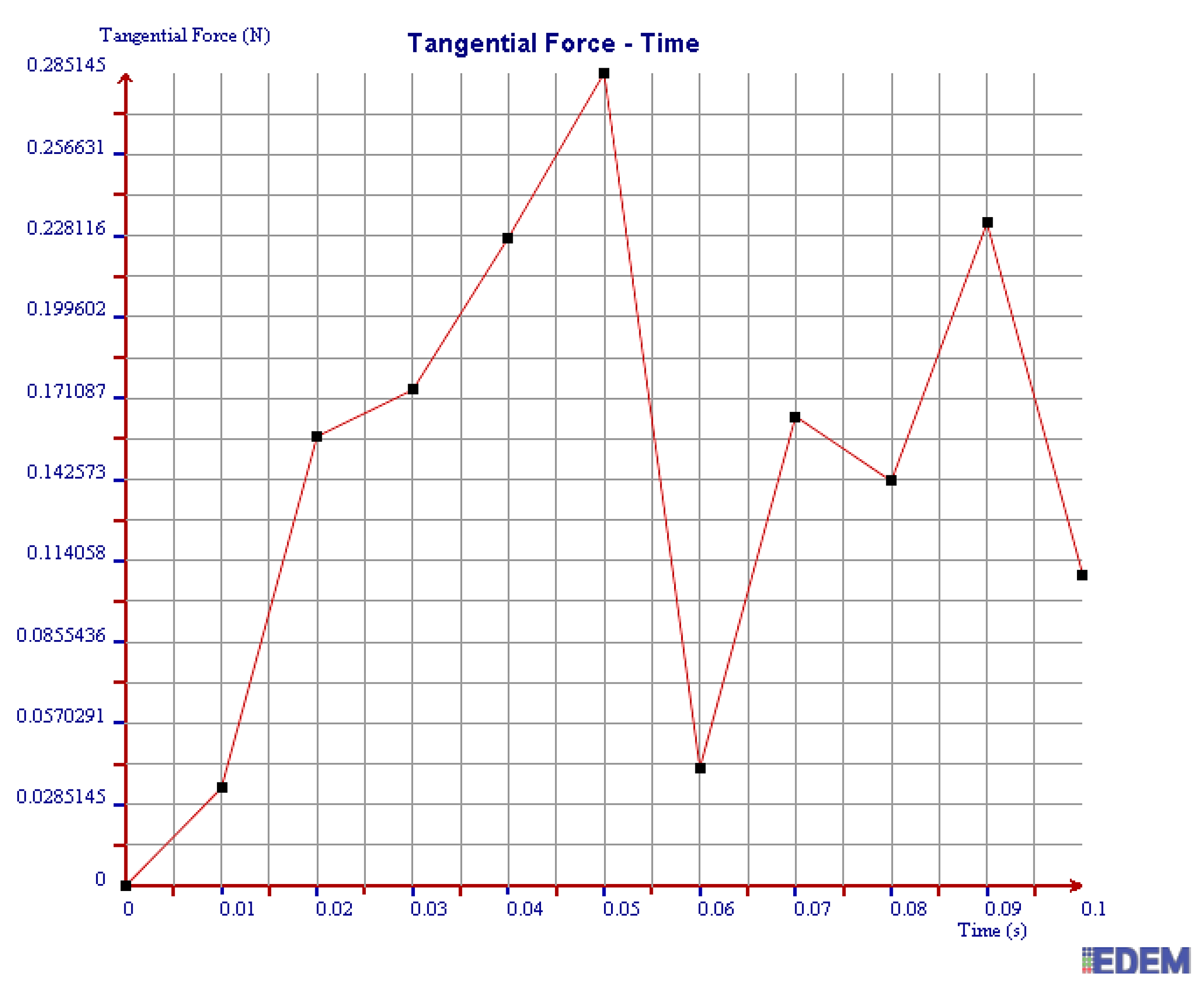



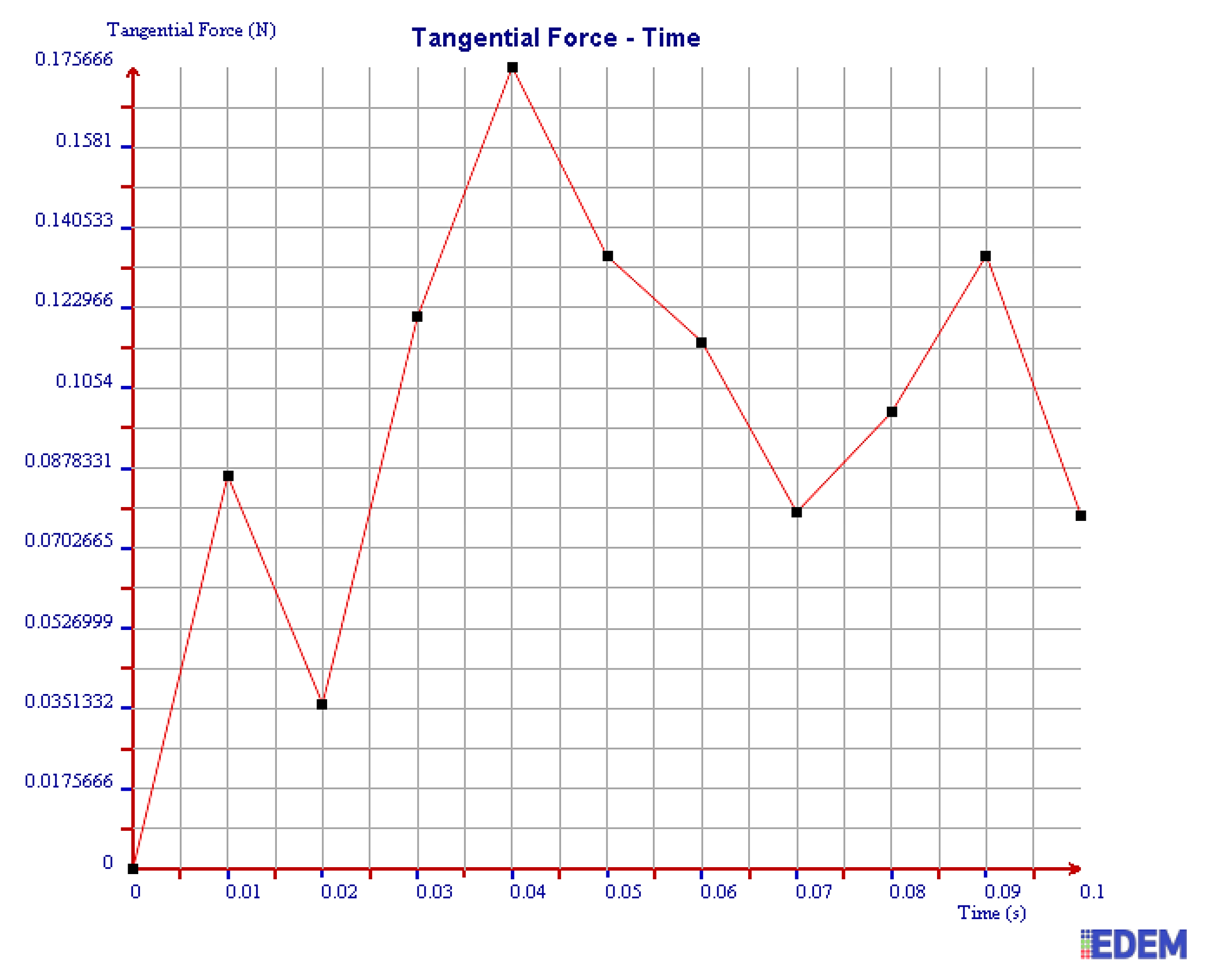










| Factors | Φ | L | H | S | K | W = S × K | |
|---|---|---|---|---|---|---|---|
| Test Numbers | |||||||
| 1 | 12 | 10.2 | 27 | 0.0144 | 10639 | 152.769 | |
| 2 | 12 | 11.2 | 29 | 0.0158 | 10789 | 170.858 | |
| 3 | 12 | 12.2 | 31 | 0.0126 | 10930 | 137.631 | |
| 4 | 13 | 10.2 | 27 | 0.0161 | 10619 | 169.904 | |
| 5 | 13 | 11.2 | 29 | 0.0159 | 10769 | 171.447 | |
| 6 | 13 | 12.2 | 31 | 0.0149 | 10914 | 163.548 | |
| 7 | 14 | 10.2 | 27 | 0.0169 | 10604 | 178.951 | |
| 8 | 14 | 11.2 | 29 | 0.0174 | 10755 | 186.778 | |
| 9 | 14 | 12.2 | 31 | 0.0162 | 10902 | 177.024 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, G.; Xu, G.; Zhang, X.; Zhang, Y.; Song, Z.; Xu, W. Study on Dynamic Monitoring of Wire Rope Tension Based on the Particle Damping Sensor. Sensors 2019, 19, 388. https://doi.org/10.3390/s19020388
Lei G, Xu G, Zhang X, Zhang Y, Song Z, Xu W. Study on Dynamic Monitoring of Wire Rope Tension Based on the Particle Damping Sensor. Sensors. 2019; 19(2):388. https://doi.org/10.3390/s19020388
Chicago/Turabian StyleLei, Gaoyang, Guiyun Xu, Xiaoguang Zhang, Yayun Zhang, Zhenyue Song, and Wentao Xu. 2019. "Study on Dynamic Monitoring of Wire Rope Tension Based on the Particle Damping Sensor" Sensors 19, no. 2: 388. https://doi.org/10.3390/s19020388
APA StyleLei, G., Xu, G., Zhang, X., Zhang, Y., Song, Z., & Xu, W. (2019). Study on Dynamic Monitoring of Wire Rope Tension Based on the Particle Damping Sensor. Sensors, 19(2), 388. https://doi.org/10.3390/s19020388





