Indoor Mapping Guidance Algorithm of Rotary-Wing UAV Including Dead-End Situations
Abstract
1. Introduction
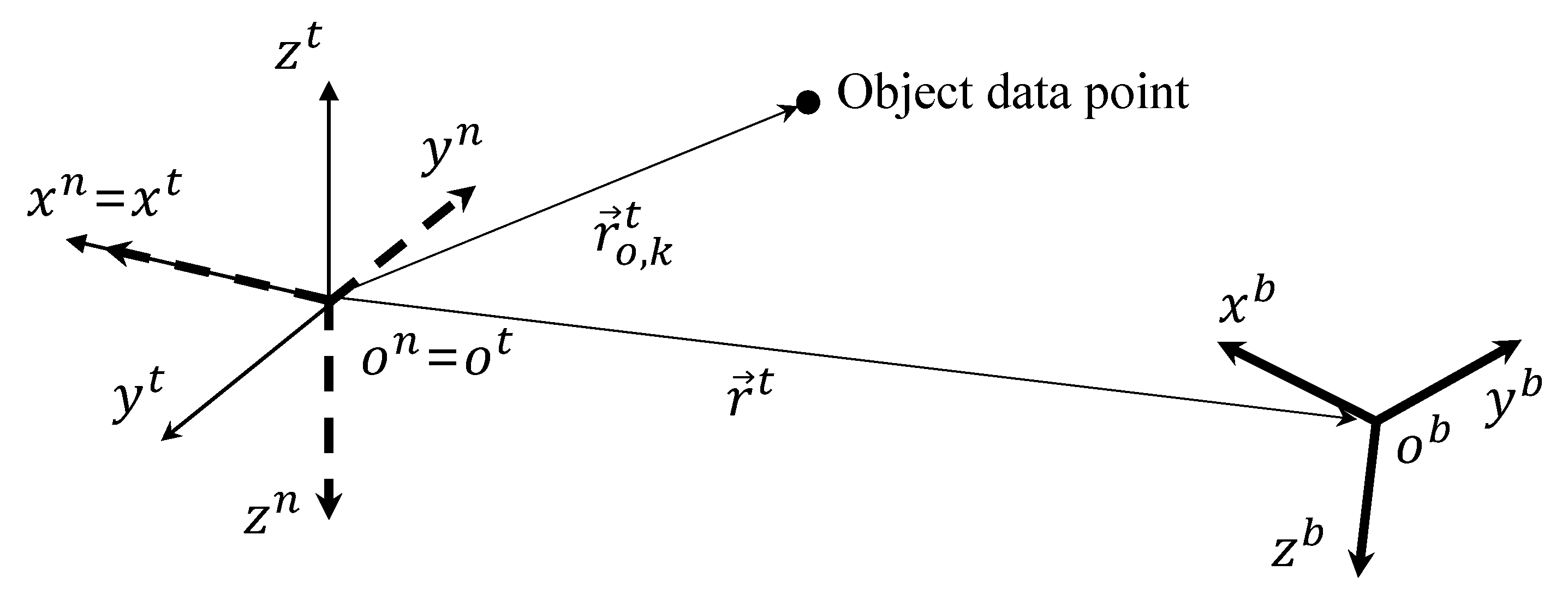
2. Unmanned Aerial Vehicle System and Its Object Data Acquisition
2.1. Dynamics
2.2. Control Structure
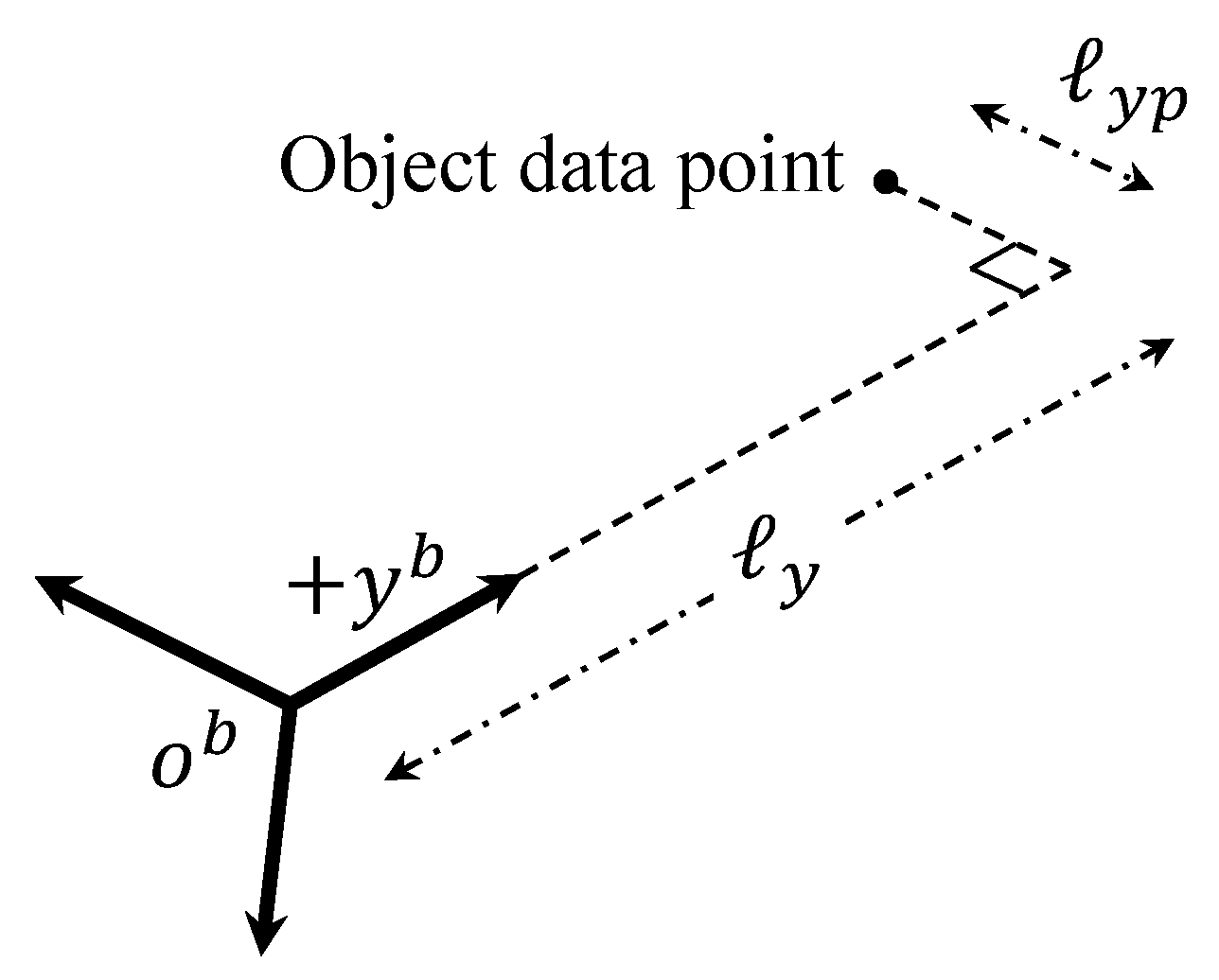
2.3. Object Data Acquisition
3. Indoor Mapping Guidance Algorithm
3.1. Velocity Vector and Yaw Commands
3.2. Velocity Magnitude Command
3.3. Exploration Completion Logic
3.4. Dead-End Situation Logic
| Algorithm 1: Overall strategy including dead-end situation. |
 |
4. Numerical Simulation
4.1. Simulation I: Single Room
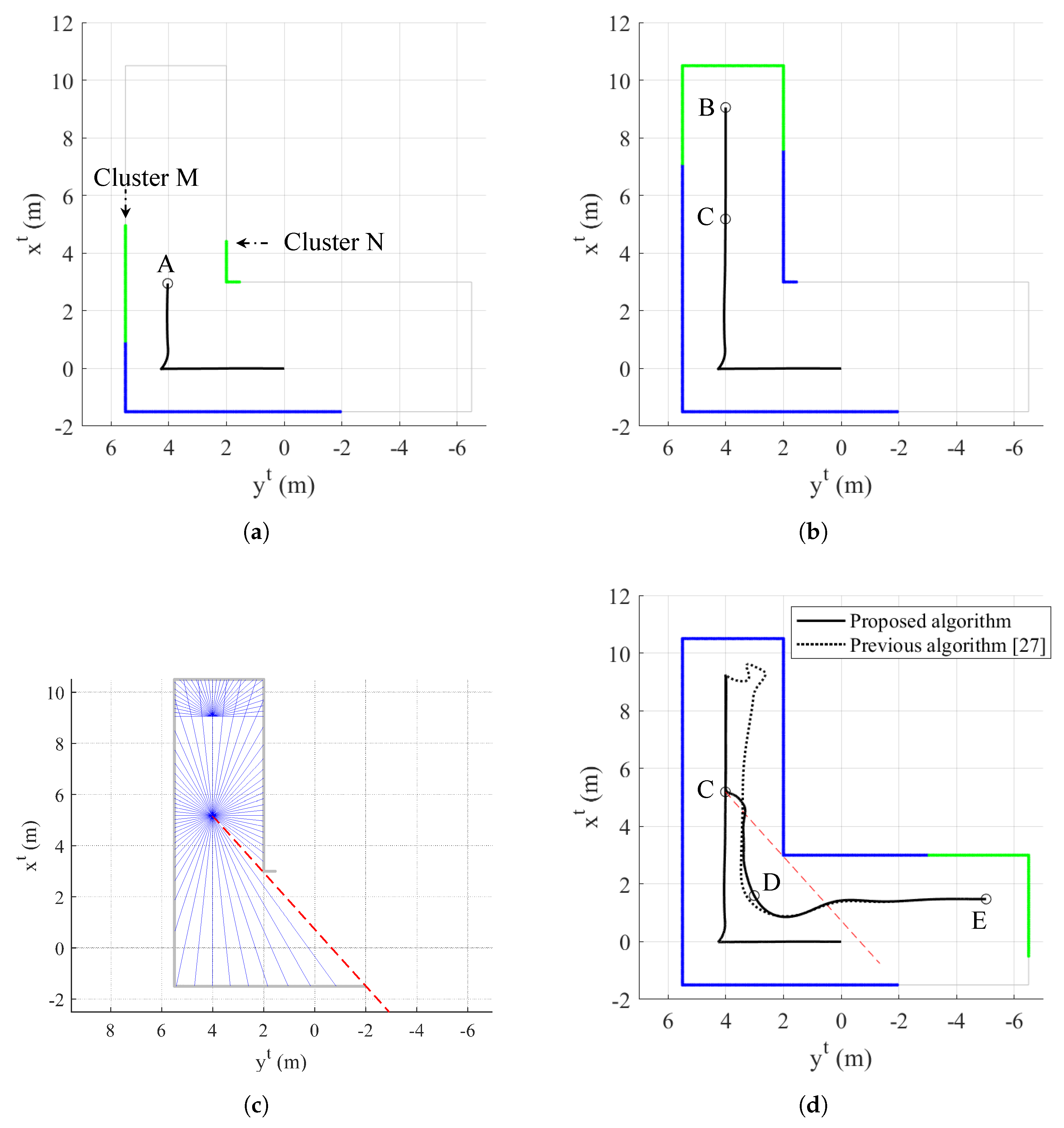
4.2. Simulation II: L-Shaped Aisle
4.3. Simulation III: Complicated Indoor Environment
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jin, R.; Jiang, J.; Qi, Y.; Lin, D.; Song, T. Drone Detection and Pose Estimation Using Relational Graph Networks. Sensors 2019, 19, 1479. [Google Scholar] [CrossRef] [PubMed]
- Koksal, N.; Jalalmaab, M.; Fidan, B. Adaptive Linear Quadratic Attitude Tracking Control of a Quadrotor UAV Based on IMU Sensor Data Fusion. Sensors 2019, 19, 46. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; He, B. Novel Fuzzy PID-Type Iterative Learning Control for Quadrotor UAV. Sensors 2019, 19, 24. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.Y.; Luo, B.; Zeng, M.; Meng, Q.H. A Wind Estimation Method with an Unmanned Rotorcraft for Environmental Monitoring Tasks. Sensors 2018, 18, 4504. [Google Scholar] [CrossRef]
- Li, B.; Zhou, W.; Sun, J.; Wen, C.Y.; Chen, C.K. Development of Model Predictive Controller for a Tail-Sitter VTOL UAV in Hover Flight. Sensors 2018, 18, 2859. [Google Scholar] [CrossRef]
- Stevens, B.L.; Lewis, F.L. Aircraft Control and Simulation; Wiley: Hoboken, NJ, USA, 2003; pp. 1–481. [Google Scholar]
- Sanca, A.S.; Alsina, P.J.; Cerqueira, J.F. Dynamic Modelling of a Quadrotor Aerial Vehicle with Nonlinear Inputs. In Proceedings of the IEEE Latin American Robotic Symposium, Natal, Brazil, 29–30 October 2008. [Google Scholar]
- Bangura, M.; Mahony, R. Nonlinear Dynamic Modeling for High Performance Control of a Quadrotor. In Proceedings of the Australasian Conference on Robotics and Automation, Wellington, New Zealand, 3–5 December 2012. [Google Scholar]
- Garcia Carrillo, L.R.; Fantoni, I.; Rondon, E.; Dzul, A. Three-Dimensional Position and Velocity Regulation of a Quad-Rotorcraft Using Optical Flow. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 358–371. [Google Scholar] [CrossRef]
- Bristeau, P.J.; Martin, P.; Salaün, E.; Petit, N. The Role of Propeller Aerodynamics in the Model of a Quadrotor UAV. In Proceedings of the European Control Conference, Budapest, Hungary, 23–26 August 2009. [Google Scholar]
- Bramwell, A.R.S.; Done, G.; Balmford, D. Bramwell’s Helicopter Dynamics; Butterworth: Oxford, UK, 2001; pp. 1–114. [Google Scholar]
- Arleo, A.; Millán, J.D.R.; Floreano, D. Efficient learning of variable-resolution cognitive maps for autonomous indoor navigation. IEEE Trans. Robot. Autom. 1999, 15, 990–1000. [Google Scholar] [CrossRef]
- Luo, R.C.; Lai, C.C. Enriched Indoor Map Construction Based on Multisensor Fusion Approach for Intelligent Service Robot. IEEE Trans. Ind. Electron. 2012, 59, 3135–3145. [Google Scholar] [CrossRef]
- Khoshelham, K.; Elberink, S.O. Accuracy and Resolution of Kinect Depth Data for Indoor Mapping Applications. Sensors 2012, 12, 1437–1454. [Google Scholar] [CrossRef]
- Wen, C.; Qin, L.; Zhu, Q.; Wang, C.; Li, J. Three-Dimensional Indoor Mobile Mapping With Fusion of Two-Dimensional Laser Scanner and RGB-D Camera Data. IEEE Geosci. Remote. Sens. Lett. 2014, 11, 843–847. [Google Scholar]
- Jung, J.; Lee, S.; Myung, H. Indoor Mobile Robot Localization and Mapping Based on Ambient Magnetic Fields and Aiding Radio Sources. IEEE Trans. Instrum. Meas. 2015, 64, 1922–1934. [Google Scholar] [CrossRef]
- Jung, J.; Yoon, S.; Ju, S.; Heo, J. Development of Kinematic 3D Laser Scanning System for Indoor Mapping and As-Built BIM Using Constrained SLAM. Sensors 2015, 15, 26430–26456. [Google Scholar] [CrossRef] [PubMed]
- dos Santos, D.R.; Basso, M.A.; Khoshelham, K.; de Oliveira, E.; Pavan, N.L.; Vosselman, G. Mapping Indoor Spaces by Adaptive Coarse-to-Fine Registration of RGB-D Data. IEEE Geosci. Remote. Sens. Lett. 2016, 13, 262–266. [Google Scholar] [CrossRef]
- Lee, K.; Ryu, S.; Yeon, S.; Cho, H.; Jun, C.; Kang, J.; Choi, H.; Hyeon, J.; Baek, I.; Jung, W.; et al. Accurate Continuous Sweeping Framework in Indoor Spaces With Backpack Sensor System for Applications to 3D Mapping. IEEE Robot. Autom. Lett. 2016, 1, 316–323. [Google Scholar] [CrossRef]
- Guerra, E.; Munguia, R.; Bolea, Y.; Grau, A. Human Collaborative Localization and Mapping in Indoor Environments with Non-Continuous Stereo. Sensors 2016, 16, 275. [Google Scholar] [CrossRef]
- Li, J.; Zhong, R.; Hu, Q.; Ai, M. Feature-Based Laser Scan Matching and Its Application for Indoor Mapping. Sensors 2016, 16, 1265. [Google Scholar] [CrossRef]
- Zhou, M.; Zhang, Q.; Wang, Y.; Tian, Z. Hotspot Ranking Based Indoor Mapping and Mobility Analysis Using Crowdsourced Wi-Fi Signal. IEEE Access 2017, 5, 3594–3602. [Google Scholar] [CrossRef]
- Jiang, L.; Zhao, P.; Dong, W.; Li, J.; Ai, M.; Wu, X.; Hu, Q. An Eight-Direction Scanning Detection Algorithm for the Mapping Robot Pathfinding in Unknown Indoor Environment. Sensors 2018, 18, 4254. [Google Scholar] [CrossRef]
- Zhou, B.; Li, Q.; Zhai, G.; Mao, Q.; Yang, J.; Tu, W.; Xue, W.; Chen, L. A Graph Optimization-Based Indoor Map Construction Method via Crowdsourcing. IEEE Access 2018, 6, 33692–33701. [Google Scholar] [CrossRef]
- Tang, S.; Li, Y.; Yuan, Z.; Li, X.; Guo, R.; Zhang, Y.; Wang, W. A Vertex-to-Edge Weighted Closed-Form Method for Dense RGB-D Indoor SLAM. IEEE Access 2019, 7, 32019–32029. [Google Scholar] [CrossRef]
- Qian, C.; Zhang, H.; Tang, J.; Li, B.; Liu, H. An Orthogonal Weighted Occupancy Likelihood Map with IMU-Aided Laser Scan Matching for 2D Indoor Mapping. Sensors 2019, 19, 1742. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Kim, Y. Horizontal-vertical guidance of Quadrotor for obstacle shape mapping. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 3024–3035. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002; pp. 505–544. [Google Scholar]
- Breu, H.; Gil, J.; Kirkpatrick, D.; Werman, M. Linear Time Euclidean Distance Transform Algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 529–533. [Google Scholar] [CrossRef]








| m | 6.2 kg | d | 2.5 m | 2.5 m | |
| 2.85 × 10 kgm | 1.5 m | 2.2 m | |||
| 2.85 × 10 kgm | 0.8 m/s | ||||
| 4.94 × 10 kgm | 0.3 m/s | ||||
| g | 9.807 m/s | 11.0 s | 0.15 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Yoo, J. Indoor Mapping Guidance Algorithm of Rotary-Wing UAV Including Dead-End Situations. Sensors 2019, 19, 4854. https://doi.org/10.3390/s19224854
Park J, Yoo J. Indoor Mapping Guidance Algorithm of Rotary-Wing UAV Including Dead-End Situations. Sensors. 2019; 19(22):4854. https://doi.org/10.3390/s19224854
Chicago/Turabian StylePark, Jongho, and Jaehyun Yoo. 2019. "Indoor Mapping Guidance Algorithm of Rotary-Wing UAV Including Dead-End Situations" Sensors 19, no. 22: 4854. https://doi.org/10.3390/s19224854
APA StylePark, J., & Yoo, J. (2019). Indoor Mapping Guidance Algorithm of Rotary-Wing UAV Including Dead-End Situations. Sensors, 19(22), 4854. https://doi.org/10.3390/s19224854





