Analysis of the Azimuth Ambiguity and Imaging Area Restriction for Circular SAR Based on the Back-Projection Algorithm
Abstract
:1. Introduction
2. Materials and Methods
2.1. CSAR Signal Model
2.2. Azimuth Ambiguity Analysis
2.3. Imaging Range Limitation
2.4. Comparison with the Traditional Method
3. Experimental Results
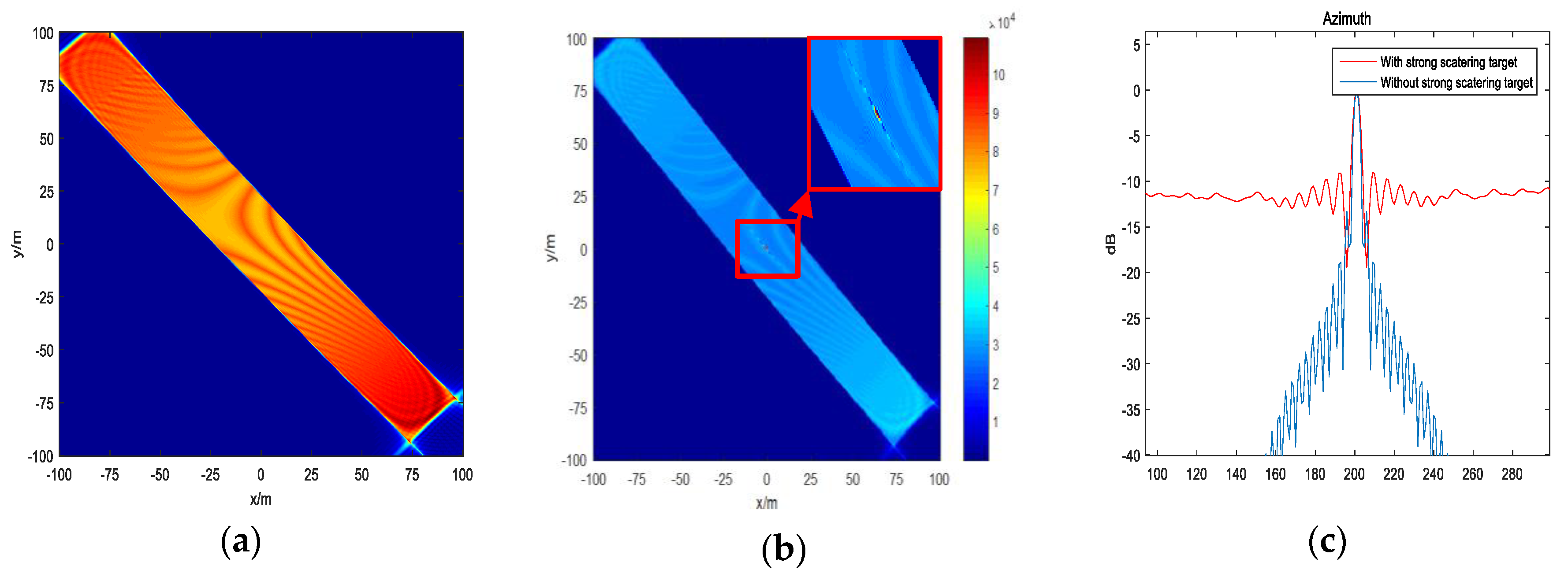
3.1. Ideal Point Simulation
3.2. Real Data Experiment
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Knaell, K.K.; Cardillo, G.P. Radar tomography for the generation of three-dimensional images. IEEE Radar, Sonar Navig. 1995, 142, 54–60. [Google Scholar] [CrossRef]
- Casteel, C.H.; Gorham, L.A.; Minardi, M.J.; Scarborough, S.; Naidu, K.D.; Majumder, U.K. A challenge problem for 2D/3D imaging of targets from a volumetric data set in an urban environment. Proc. SPIE 2007, 6568, 65680D. [Google Scholar]
- Ertin, E.; Austin, C.D.; Sharma, S.; Moses, R.L.; Potter, L.C. GOTCHA Experience Report: Three-Dimensional SAR Imaging Complete Circular Apertures. Proc. SPIE 2007, 6568, 656802. [Google Scholar]
- Ponce, O.; Prats, P.I.; Pinheiro, M.; Rodriguez-Cassola, M.; Scheiber, R.; Reigber, A.; Moreira, A. Fully polarimetric high-resoution 3-D imaging with circular SAR at L-band. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3074–3090. [Google Scholar] [CrossRef]
- Ponce, O.; Prats, P.; Scheiber, R.; Reigber, A.; Moreira, A. First airborne demonstration of holographic SAR tomography with fully polarimetric multicircular acquisitions at L-band. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6170–6196. [Google Scholar] [CrossRef]
- Cantalloube, H.; Koeniquer, E.C.; Oriot, H. High resolution SAR imaging along circular trajectories. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 850–853. [Google Scholar]
- Lin, Y.; Hong, W.; Tan, W.; Wang, Y.; Xiang, M. Airborne circular SAR imaging: Results at P-band. Geoscience & Remote Sensing Symposium. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5594–5597. [Google Scholar]
- Soumekh, M. Synthetic Aperture Radar Signal Processing: With MATLAB Algorithms; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Desai, M.; Jenkins, W. Convolution backprojection image reconstruction for spotlight mode synthetic aperture radar. IEEE Trans. Image Process. A Publ. IEEE Signal Process. Soc. 1992, 1, 505–517. [Google Scholar] [CrossRef] [PubMed]
- Ulander, L.M.H.; Hellsten, H.; Stenstrom, G. Synthetic-aperture radar processing using fast factorized back-projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef] [Green Version]
- Vu, V.T.; Sjogren, T.K.; Pettersson, M.I. A comparison between fast factorized backprojection and frequency-domain algorithms in UWB low frequency SAR. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; pp. IV-1284–IV-1287. [Google Scholar]
- Jakowatz, C.V., Jr.; Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Thompson, P.A. Spotlight-Mode Synthetic Aperture Radar: A Signal Processing Approach; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996; pp. 330–332. [Google Scholar]
- Soumekh, M. Synthetic Aperture Radar Signal Processing; John Wiley & Sons, Inc.: New York, NY, USA, 1999; pp. 486–539. [Google Scholar]







| Parameter | Value |
|---|---|
| Carrier Frequency | 5.4 GHz |
| Pause Width | 20 us |
| Band Width | 560 MHz |
| Sample Frequency | 1.5 GHz |
| Pause Repeat Frequency(PRF) | 1200 Hz |
| Velocity | 80 m/s |
| Platform Height | 3000 m |
| Radius | 5000 m |
| Sub aperture Size | About 2 |
| Reference Height | 0 m |
| Slow time |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, B.; Qiu, X.; Huang, L.; Lei, S.; Lei, B.; Ding, C. Analysis of the Azimuth Ambiguity and Imaging Area Restriction for Circular SAR Based on the Back-Projection Algorithm. Sensors 2019, 19, 4920. https://doi.org/10.3390/s19224920
Du B, Qiu X, Huang L, Lei S, Lei B, Ding C. Analysis of the Azimuth Ambiguity and Imaging Area Restriction for Circular SAR Based on the Back-Projection Algorithm. Sensors. 2019; 19(22):4920. https://doi.org/10.3390/s19224920
Chicago/Turabian StyleDu, Bang, Xiaolan Qiu, Lijia Huang, Songlin Lei, Bin Lei, and Chibiao Ding. 2019. "Analysis of the Azimuth Ambiguity and Imaging Area Restriction for Circular SAR Based on the Back-Projection Algorithm" Sensors 19, no. 22: 4920. https://doi.org/10.3390/s19224920
APA StyleDu, B., Qiu, X., Huang, L., Lei, S., Lei, B., & Ding, C. (2019). Analysis of the Azimuth Ambiguity and Imaging Area Restriction for Circular SAR Based on the Back-Projection Algorithm. Sensors, 19(22), 4920. https://doi.org/10.3390/s19224920





