GPS-SLAM: An Augmentation of the ORB-SLAM Algorithm
Abstract
:1. Introduction
2. Materials and Methods
2.1. Brief Description of ORB-SLAM
2.2. SLAM Algorithms and the GPS Data
2.3. The Modifications Leading to GPS-SLAM
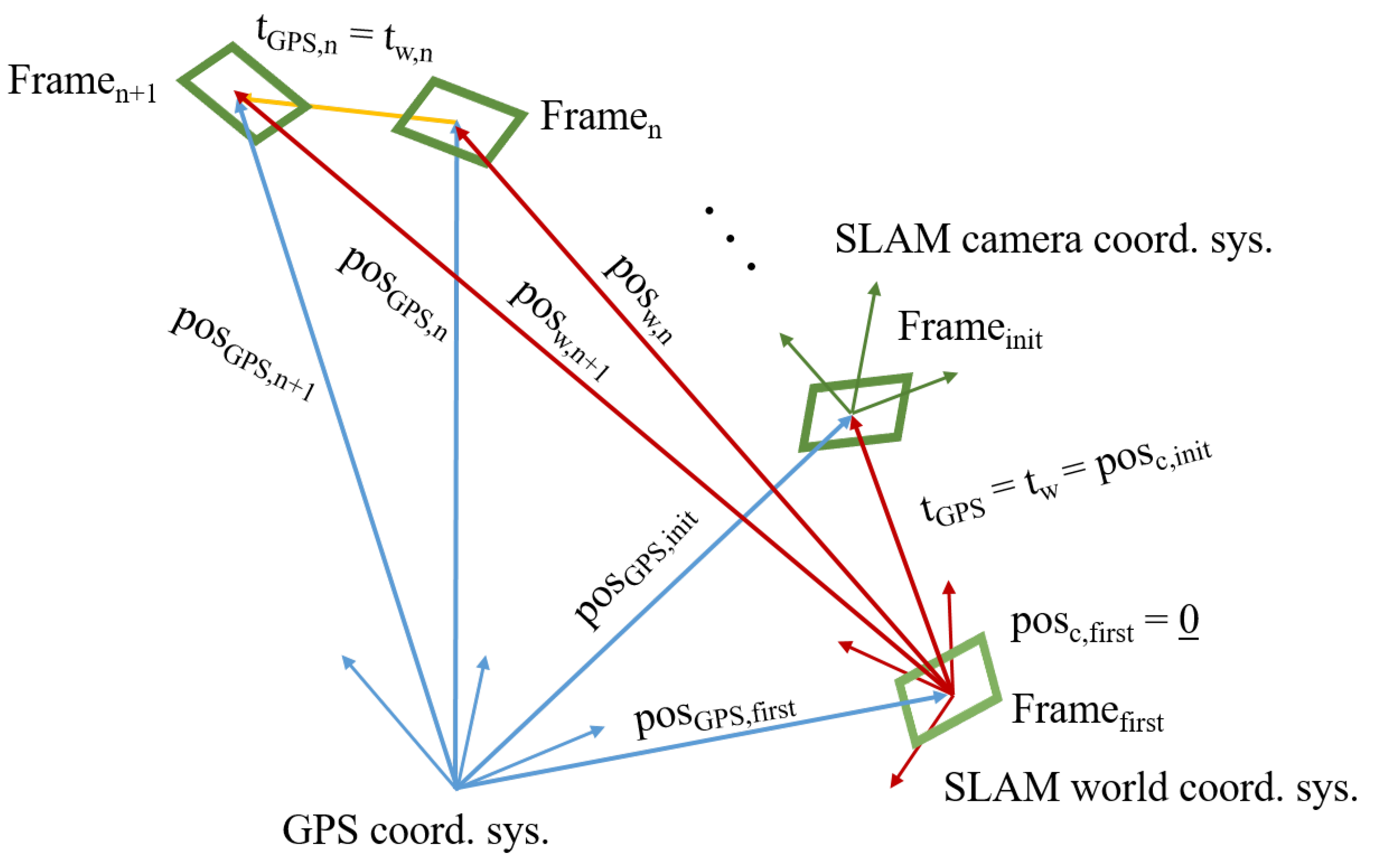
2.3.1. Using the GPS Data
- SLAM world coordinate system (fix)—noted with w
- SLAM camera coordinate system (changes)—noted with c
- GPS coordinate system (fix)—noted with GPS
2.3.2. Modification of the “TrackReferenceKeyFrame” Method
2.3.3. Relocalization Candidates Determined by the Position of the Frames
2.4. The Dataset
3. Results and Discussion
3.1. The Experiment Design
3.2. Aspects of Comparison
- Last Tracked Frame
- Lost (times)
- Number of Lost Frames
- Lost Frames per Losses
- Number of Calls to TrackReferenceKeyFrame
- Number of Erroneous Frames
- Number of Map Points
- Percentage of False Map Points
- Mean Tracking Time
- Standard Deviation of Tracking Time
- Median of Tracking Time
- Mean Relocalization Time
- a frame which is not in the plane of the UAV flight
- a frame with erroneous orientation
3.3. Comparison of the Algorithms Using 2000 Features
3.4. Comparison of the Algorithms Using 6000 Features
3.5. Comparison of ORB-SLAM Using 2000 and 6000 Features
3.6. Comparison of the GPS-SLAM Using 2000 and 6000 Features
3.7. Comparison of the Best Settings of ORB-SLAM and GPS-SLAM
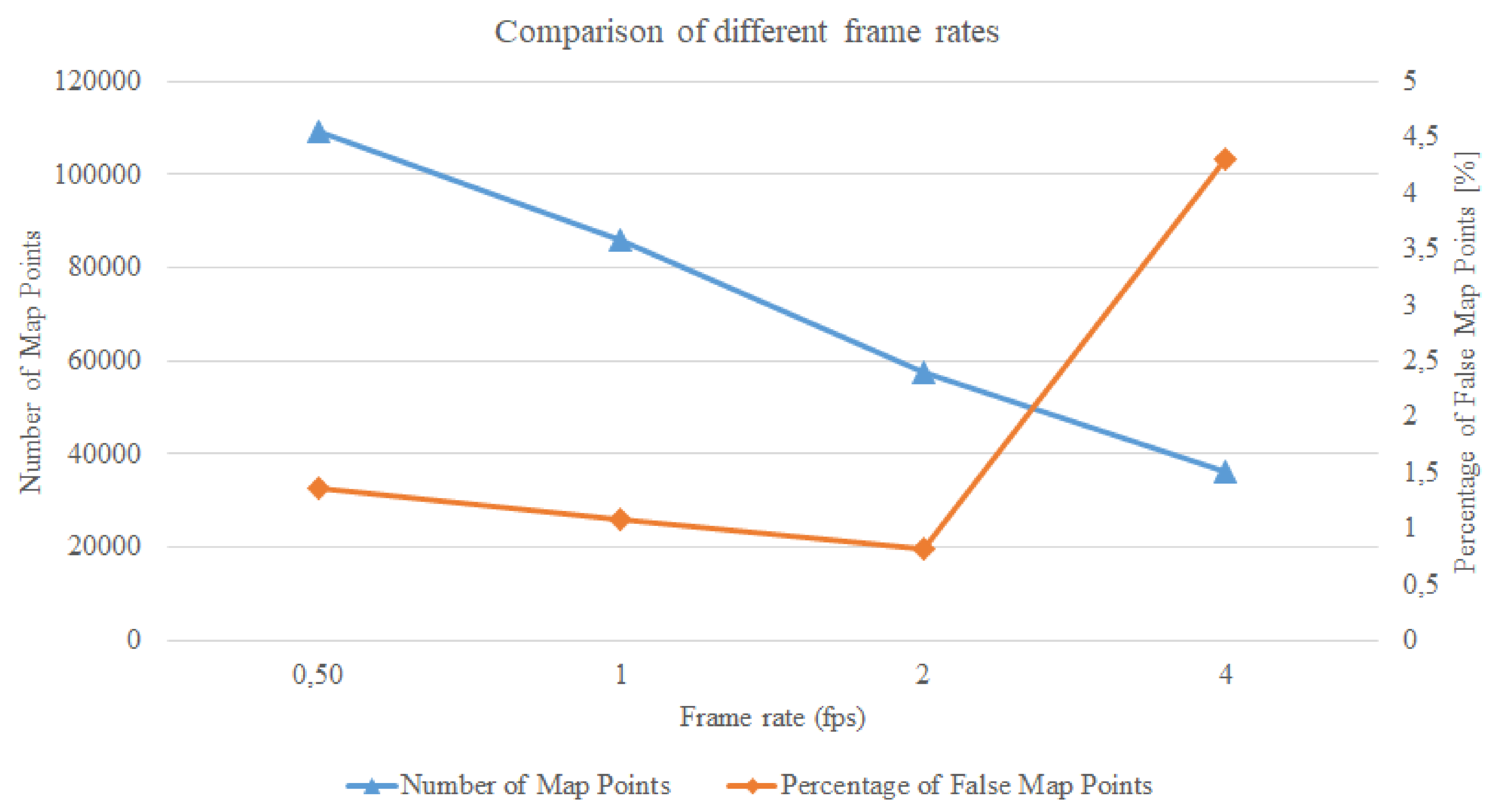
3.8. Frame Rates—Fastest Execution with Good Results
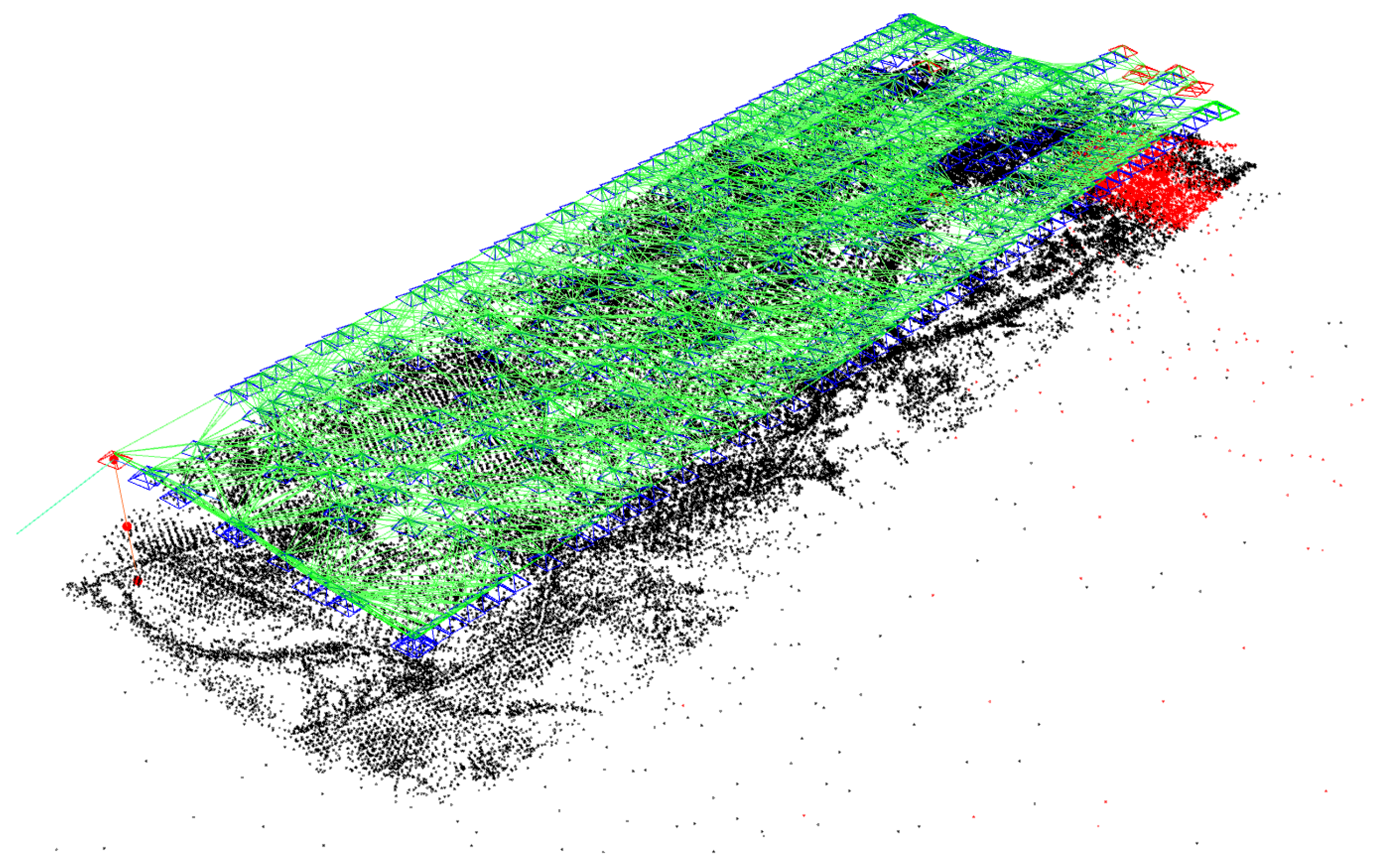
3.9. 3D Map Creation from the Map Points
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| GPS | Global Positioning System |
| SLAM | Simultaneous Localization and Mapping |
| fps | frames per second |
| IMU | Inertial Measurement Unit |
| UAV | Unmanned Aerial Vehicle |
| GNSS | Global Navigation Satellite System |
Appendix A
Appendix A.1. The Calculation of the Rotation Matrix between the Coordinate Systems of SLAM and GPS in Tracking.cc in Method CreateInitialMapMonocular
Appendix A.2. GPS Data: Calculating the Parts of the Transformation Matrix etween Two Frames in Tracking.cc in Method Track
- mCurrentFrame.mtransGPS.rowRange(0,3).colRange(0,3) =
- mCurrentFrame.mT_GPS.rowRange(0,3).colRange(0,3) *
- (mLastFrame.mT_GPS.rowRange(0,3).colRange(0,3)).inv();
- mCurrentFrame.mtransGPS.rowRange(0,3).col(3) =
- mCurrentFrame.mT_GPS.rowRange(0,3).col(3) -
- mLastFrame.mT_GPS.rowRange(0,3).col(3);
Appendix A.3. Determination of the next camera pose in Tracking.cc in method TrackWithGPSData (Line 1242)
References
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Klein, G.; Murray, D. Parallel tracking and mapping for small AR workspaces. In Proceedings of the 2007 6th IEEE and ACM International Symposium on Mixed and Augmented Reality, IEEE Computer Society, Washington, DC, USA, 13–16 November 2007; pp. 1–10. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G.R. ORB: An efficient alternative to SIFT or SURF. ICCV Citeseer 2011, 11, 2. [Google Scholar]
- Taketomi, T.; Uchiyama, H.; Ikeda, S. Visual SLAM algorithms: A survey from 2010 to 2016. IPSJ Trans. Comput. Vis. Appl. 2017, 9, 16. [Google Scholar] [CrossRef]
- Salamí, E.; Gallardo, A.; Skorobogatov, G.; Barrado, C. On-the-Fly Olive Trees Counting Using a UAS and Cloud Services. Remote Sens. 2019, 11, 316. [Google Scholar] [CrossRef]
- Li, J.; Bi, Y.; Lan, M.; Qin, H.; Shan, M.; Lin, F.; Chen, B.M. Real-time simultaneous localization and mapping for uav: A survey. In Proceedings of the International micro air vehicle competition and conference, Beijing, China, 17–21 October 2016; pp. 237–242. [Google Scholar]
- Montemerlo, M.; Thrun, S.; Koller, D.; Wegbreit, B. ; others. In FastSLAM 2.0: An improved particle filtering algorithm for simultaneous localization and mapping that provably converges. In Proceedings of the Eighteenth International Joint Conference on Artificial Intelligence, Acapulco, Mexico, 9–15 August 2003; pp. 1151–1156. [Google Scholar]
- Vassallo, C.; Tabib, W.; Peterson, K. Orbital SLAM. In Proceedings of the 2015 12th Conference on Computer and Robot Vision, IEEE, Halifax, NS, Canada, 3–5 June 2015; pp. 305–312. [Google Scholar]
- Klein, G.; Murray, D. Parallel tracking and mapping on a camera phone. In Proceedings of the 2009 8th IEEE International Symposium on Mixed and Augmented Reality, IEEE, Orlando, FL, USA, 19–22 October 2009; pp. 83–86. [Google Scholar]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Cham, Switzerland, 2014; pp. 834–849. [Google Scholar]
- Scaramuzza, D.; Fraundorfer, F. Visual odometry [tutorial]. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar] [CrossRef]
- Kleinert, M.; Schleith, S. Inertial aided monocular SLAM for GPS-denied navigation. In Proceedings of the 2010 IEEE Conference on Multisensor Fusion and Integration, IEEE, Salt Lake City, UT, USA, 5–7 September 2010; pp. 20–25. [Google Scholar]
- Bu, S.; Zhao, Y.; Wan, G.; Liu, Z. Map2DFusion: Real-time incremental UAV image mosaicing based on monocular slam. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), IEEE, Daejeon, Korea, 9–14 October 2016; pp. 4564–4571. [Google Scholar]
- Schmuck, P.; Chli, M. Multi-uav collaborative monocular slam. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), IEEE, Singapore, 29 May–3 June 2017; pp. 3863–3870. [Google Scholar]
- Vallet, J.; Panissod, F.; Strecha, C.; Tracol, M. Photogrammetric performance of an ultra light weight swinglet UAV. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2011, 38. [Google Scholar] [CrossRef]
- De Reu, J.; Plets, G.; Verhoeven, G.; De Smedt, P.; Bats, M.; Cherretté, B.; De Maeyer, W.; Deconynck, J.; Herremans, D.; Laloo, P.; et al. Towards a three-dimensional cost-effective registration of the archaeological heritage. J. Archaeol. Sci. 2013, 40, 1108–1121. [Google Scholar] [CrossRef]
- Rosten, E.; Drummond, T. Fusing points and lines for high performance tracking. ICCV Citeseer 2005, 2, 1508–1515. [Google Scholar]








| Aspects of Comparison | ORB-SLAM | GPS-SLAM | Imp. | In % | p-Value |
|---|---|---|---|---|---|
| Last Tracked Frame | 750.67 | 768.6 | ✓ | +2.39% | 7.8 |
| Lost (times) | 7.08 | 12.3 | ✗ | −73.7% | 0.0666 |
| Number of Lost Frames | 280 | 76.2 | ✓ | +72.8% | 9.6 |
| Lost Frames per Losses | 39.55 | 6.20 | ✓ | +84.3% | 2.2 |
| N. of Calls to TrackReferenceKeyFrame | 31.75 | 20.4 | ✓ | +35.7% | 0.0392 |
| Number of Erroneous Frames | 11.67 | 8.9 | ✓ | +23.7% | 0.31 |
| Number of Map Points | 30,391 | 82,614 | ✓ | +172% | 2.07 |
| Percentage of False Map Points | 1.45% | 7.84% | ✗ | −441% | 0.0431 |
| Mean Tracking Time [s] | 0.03311 | 0.06020 | ✗ | −81.8% | 1.51 |
| StdDev of Tracking Time [s] | 0.01152 | 0.02921 | ✗ | −154% | 2.08 |
| Median of Tracking Time [s] | 0.03103 | 0.05514 | ✗ | −77.7% | 9.6 |
| Mean Relocalization Time [s] | 0.01489 | 0.07657 | ✗ | −414% | 3.82 |
| 2000 features extracted | |||||
| Aspects of Comparison | ORB-SLAM | GPS-SLAM | Imp. | In % | p-Value |
|---|---|---|---|---|---|
| Last Tracked Frame | 754.92 | 769 | ✓ | +1.87% | 5.88 notation. |
| Lost (times) | 10 | 6.7 | ✓ | +33% | 1.01 |
| Number of Lost Frames | 172.67 | 44.4 | ✓ | +74.3% | 1.73 |
| Lost Frames per Losses | 17.27 | 6.63 | ✓ | +61.6% | 1.86 |
| N. of Calls to TrackReferenceKeyFrame | 44.5 | 13 | ✓ | +70.8% | 8.5 |
| Number of Erroneous Frames | 69.5 | 2.4 | ✓ | +96.5% | 7.39 |
| Number of Map Points | 79,127 | 109,087 | ✓ | +37.8% | 8.95 |
| Percentage of False Map Points | 8.60% | 0.72% | ✓ | +91.6% | 7.06 |
| Mean Tracking Time [s] | 0.06270 | 0.09030 | ✗ | −44.0% | 1.0 |
| StdDev of Tracking Time [s] | 0.03285 | 0.05320 | ✗ | −61.9% | 3.28 |
| Median of Tracking Time [s] | 0.05753 | 0.08094 | ✗ | −40.7% | 9.9 |
| Mean Relocalization Time [s] | 0.03858 | 0.09523 | ✗ | −147% | 1.73 |
| 6000 features extracted | |||||
| Aspects of Comparison | ORB 2000 | ORB 6000 | Improvement |
|---|---|---|---|
| Last Tracked Frame | 750.67 | 754.92 | ✓ |
| Lost (times) | 7.08 | 10 | ✗ |
| Number of Lost Frames | 280 | 172.67 | ✓ |
| Lost Frames per Losses | 39.60 | 17.27 | ✗ |
| N. of Calls to TrackReferenceKeyFrame | 31.75 | 44.5 | ✗ |
| Number of Erroneous Frames | 11.67 | 69.5 | ✗ |
| Number of Map Points | 30,391 | 79,126.9 | ✓ |
| Percentage of False Map Points | 1.45% | 8.60% | ✗ |
| Mean Tracking Time [s] | 0.03311 | 0.06270 | ✗ |
| StdDev of Tracking Time [s] | 0.01152 | 0.03285 | ✗ |
| Median of Tracking Time [s] | 0.03103 | 0.05753 | ✗ |
| Mean Relocalization Time [s] | 0.01489 | 0.03858 | ✗ |
| Aspects of Comparison | GPS 2000 | GPS 6000 | Improvement |
|---|---|---|---|
| Last Tracked Frame | 768.6 | 769 | ✓ |
| Lost (times) | 12.3 | 6.7 | ✓ |
| Number of Lost Frames | 76.2 | 44.4 | ✓ |
| Lost Frames per Losses | 6.20 | 6.63 | ✗ |
| N. of Calls to TrackReferenceKeyFrame | 20.4 | 13 | ✓ |
| Number of Erroneous Frames | 8.9 | 2.4 | ✓ |
| Number of Map Points | 82,614 | 109,087 | ✓ |
| Percentage of False Map Points | 7.84% | 0.72% | ✓ |
| Mean Tracking Time [s] | 0.06020 | 0.09027 | ✗ |
| StdDev of Tracking Time [s] | 0.02921 | 0.05319 | ✗ |
| Median of Tracking Time [s] | 0.05514 | 0.08094 | ✗ |
| Mean Relocalization Time [s] | 0.07657 | 0.09523 | ✗ |
| Aspects of Comparison | ORB 2000 | GPS 6000 | Improvement |
|---|---|---|---|
| Last Tracked Frame | 750.67 | 769 | ✓ |
| Lost (times) | 7.08 | 6.7 | ✓ |
| Number of Lost Frames | 280 | 44.4 | ✓ |
| Lost Frames per Losses | 39.55 | 6.63 | ✓ |
| N. of Calls to TrackReferenceKeyFrame | 31.75 | 13 | ✓ |
| Number of Erroneous Frames | 11.67 | 2.4 | ✓ |
| Number of Map Points | 30,391 | 109,087 | ✓ |
| Percentage of False Map Points | 1.45% | 0.72% | ✓ |
| Mean Tracking Time [s] | 0.03311 | 0.09027 | ✗ |
| StdDev of Tracking Time [s] | 0.01152 | 0.05319 | ✗ |
| Median of Tracking Time [s] | 0.03103 | 0.08094 | ✗ |
| Mean Relocalization Time [s] | 0.01489 | 0.09523 | ✗ |
| Final comparison for the best working versions | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiss-Illés, D.; Barrado, C.; Salamí, E. GPS-SLAM: An Augmentation of the ORB-SLAM Algorithm. Sensors 2019, 19, 4973. https://doi.org/10.3390/s19224973
Kiss-Illés D, Barrado C, Salamí E. GPS-SLAM: An Augmentation of the ORB-SLAM Algorithm. Sensors. 2019; 19(22):4973. https://doi.org/10.3390/s19224973
Chicago/Turabian StyleKiss-Illés, Dániel, Cristina Barrado, and Esther Salamí. 2019. "GPS-SLAM: An Augmentation of the ORB-SLAM Algorithm" Sensors 19, no. 22: 4973. https://doi.org/10.3390/s19224973
APA StyleKiss-Illés, D., Barrado, C., & Salamí, E. (2019). GPS-SLAM: An Augmentation of the ORB-SLAM Algorithm. Sensors, 19(22), 4973. https://doi.org/10.3390/s19224973







