1. Introduction
With the widespread use of wearable smart devices, sport-related activity monitoring using inertial sensors has become an active area of research, and it is used to improve the quality of life and promote personal health. In previous studies, the activity monitoring problem has often been defined as a human activity recognition (HAR) task [
1]. An HAR model usually consists of two main parts—data segmentation and activity classification. The segmentation procedure uses a fixed-length sliding window to divide the sensor signal into different segments. The subsequent classifier is then used to classify these activities by using the information in these segments. Many researchers [
2,
3,
4,
5] have used this segmentation method to identify activities with strong periodicity and a single motion state because, after segmentation, each segment contains a meaningful motion state. However, many sports are characterized by complex motion states and non-periodicity. If such an activity signal is segmented with this sliding window, there is no guarantee that each segment will contain a useful motion state. Some segments may contain only noise. Therefore, for complex activities, an activity monitoring algorithm needs the ability to detect the duration of each meaningful motion state and then identify them.
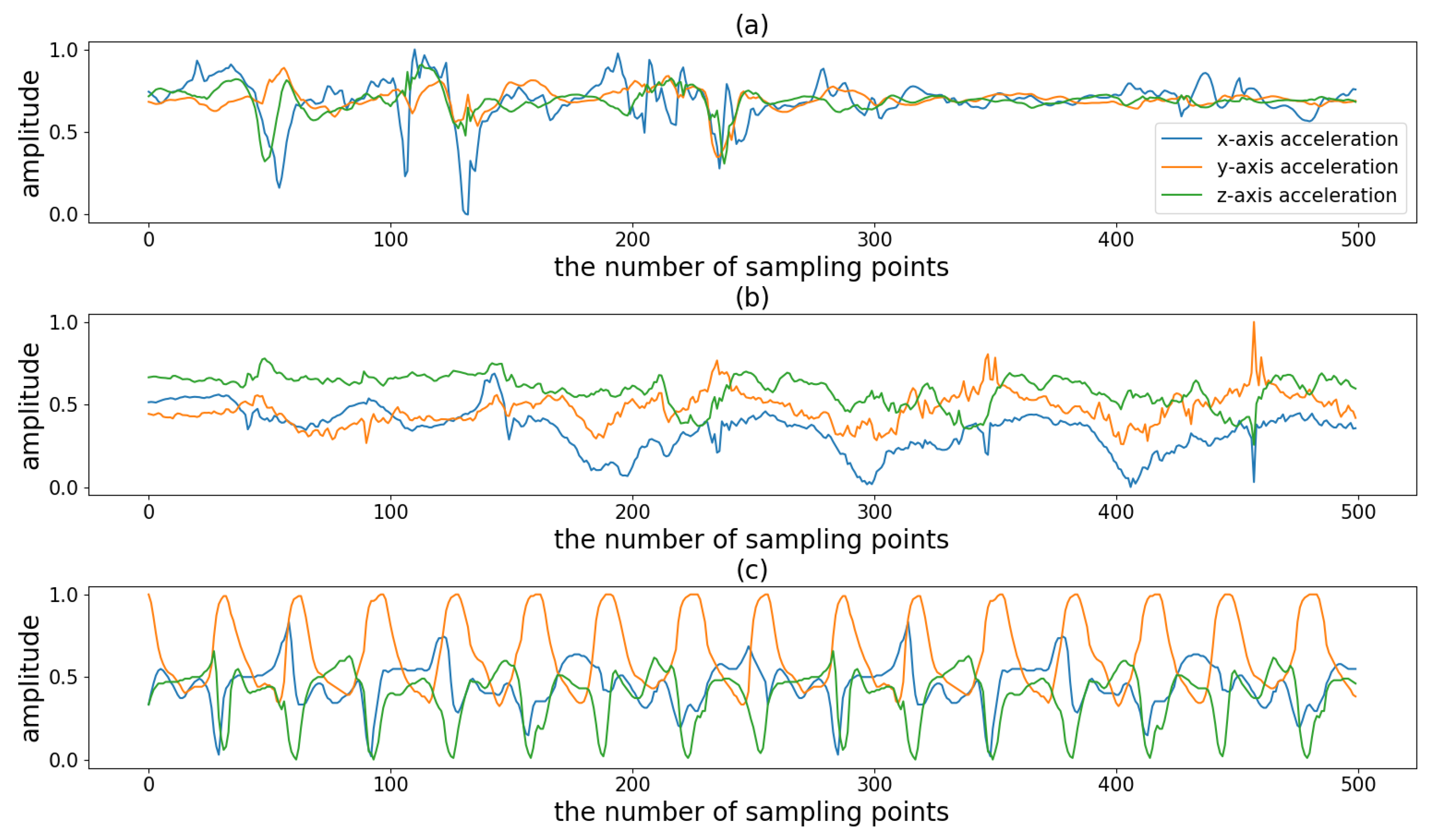
There are many kinds of sports and in this study we divided them into three types according to their periodicity and complexity.
Figure 1 shows an example of three sports. The first type is the non-periodic activity with complex motion states (NP_CMS), such as badminton and basketball. When playing this type of sport, people do not repeat the periodic motion state but randomly switch between various motion states. For example, when playing badminton, people randomly switch between serving, swinging, smashing and other motion states. In other words, the activity involves multiple motion states, each of which does not loop but instead transitions to another state. The difficulty in monitoring this type of sport is accurately detecting the duration of different motion states. The second type is the activity with weak periodicity and complex motion states (WP_CMS). This type of activity also has multiple motion states and each state may occur in a continuous loop or may be converted to another state. Moreover, the cycle is not fixed and may vary from person to person. Even for the same person, the cycle may change at different times. For example, when swimming, people change their swimming strokes from time to time. Moreover, even if the same stroke is repeated, the frequency of the motion is not uniform. Because the motion state of these activities changes frequently, for better monitoring it is important to accurately determine the duration of each cycle for each motion state. The third type is the activity with strong periodicity and a single state, such as walking and jogging. This type of activity contains only one motion state, and the cycle of the motion state is more stable.
In previous HAR studies, most researchers have used the sliding window method to segment the motion signal and obtain good recognition performance. Ponce et al. [
6] classified some daily activities, including sitting, standing, lying down, lying on one side and playing basketball. They used a 5 s sliding window to divide the sensor signal containing the target activity into different signal segments for training and test sets. They then trained an artificial hydrocarbon network to classify these labeled segments. Although their algorithms successfully identified basketball (a non-periodic activity with complex motion states), they only recognized that the user was playing basketball. We believe that meaningful motion states (such as shooting and smashing) should be accurately detected and identified to better monitor activities such as basketball. Attal et al. [
7] applied four classification algorithms to classify 11 daily activities, such as standing, sitting, sitting down, and lying down. They also used a sliding window to segment the sensor signal and selected the segments containing the target activities for training and testing. Because they lacked training signal segments containing non-target activities, they were easily misclassified. Therefore, for these non-periodic activities, we propose a method that first detects the target motion states and then identifies them. This method can effectively detect the target motion state and reduce misclassification.
For activities with weak periodicity and complex motion states (such as swimming), many researchers have explored the sliding window-based activity recognition task. Siirtola et al. [
8] applied an linear discriminant analysis (LDA) classifier to identify swimming strokes by acceleration data sampling at 5 Hz; then, they counted the number of each stroke using the peak count. Jensen et al. [
9] compared the performance of four classification methods on the basis of different sliding window lengths and sampling rates. Brunner et al. [
10] also used a sliding window to divide the sensor signal and then employed a convolutional neural network (CNN) as a classifier to recognize swimming strokes. They all had good recognition performance but they used a fixed-length sliding window to divide the swimming signal, which resulted in an inconsistent number of cycles per window and a different signal at the beginning of each window. These differences increase the difficulty of correctly classifying these movements. In particular, when the sliding window contains two strokes, the movement is easily misclassified. Therefore, in this work, we propose a classification-based periodic matching method to accurately detect one period of each stroke (motion state). First, a single-cycle candidate motion state signal is detected and inputted into a classifier. The classification result is then used to adjust the detection to obtain a more accurate period segmentation. In
Section 4.2.1, the experimental results show that the recognition performance could be improved by combining the periodic matching method. Therefore, in this paper, we regard the monitoring of NP_CMS and WP_CMS activities as a human activity detection and recognition (HADR) task.
In recent years, the CNN [
11] has developed rapidly and is widely used to improve the performance of HAR [
12,
13]. This indicates that CNNs can effectively extract the local dependency and interrelation between sensor signals. However, most algorithms simply use CNNs as a classifier and do not give them more deformation and expansion functions, as in the field of computer vision [
14,
15,
16,
17]. For example, in the field of object detection, Ren et al. [
18] skillfully applied two convolutional layers instead of fully connected layers and proposed the region of interest (RoI) pooling layer to turn target detection tasks into the generation and recognition of candidate boxes. Inspired by this, we believe that the monitoring of the activity with non-periodic and complex motion states can be understood as the detection and recognition of target motion states in a long time-series. Using Faster R-CNN [
18], we developed a candidate interval generation method in Reference [
19]. In contrast to our previous work, in this study, we added adaptive components that allow our network to process sensor data of any length. By generating candidate intervals, our network can accurately determine the full duration of a single motion state for activity detection. Activity recognition is then implemented using these candidate intervals. The proposed approach is called the interval-based activity detection and recognition method. The experimental results show that this method reduces the difficulty and improves the accuracy of recognition. Furthermore, most of the work in activity detection and recognition can be achieved by reusing the same neural network, which greatly reduces the computational cost.
Additionally, we believe that the weak periodicity of the second type of activity can be utilized to detect the duration of each motion state. Therefore, we propose an adaptive detection method based on periodic matching. The method first finds a signal containing more than one period of motion state and divides it into several signals that contain only one period. A CNN is then used for identification and the periodic matching is adaptively adjusted by the classification result. We call this approach the classification-based periodic matching method.
We only found two public datasets containing non-periodic activity with complex motion states, namely, Physical Activity Monitoring for Aging People dataset (PAMAP2) [
20] and Daily and Sports Activity dataset (DSA) [
21]. Both of them lack annotations of the duration of meaningful motion states. Therefore, we collected two activity datasets (described in
Section 2.1) for the two kinds of sports studied in this work. Instead of professional sports monitoring, we focus on providing convenient daily sports-related activity monitoring. Considering that smartwatches are widely used as wearable devices for remote health monitoring and are user-friendly [
22,
23,
24], we chose smartwatches as activity acquisition devices.
In this paper, we focus on the detection and recognition of two complex activities. In summary, this research makes the following contributions. First, for the non-periodic activity with complex motion states, we propose a motion state detection and recognition method based on interval generation. Second, for the activity with weak periodicity and complex motion states, we propose a recognition method based on periodic matching. Finally, we conducted experiments on two datasets to demonstrate that the proposed methods can effectively detect the target motion states and improve recognition performance.
5. Conclusions
In this paper, we focus on the detection and recognition of two types of activities, namely, the non-periodic activity with complex motion states (NP_CMS) and the weakly periodic activity with complex motion states (WP_CMS). In contrast to many existing HAR methods, we consider the sport-related activity monitoring problem to be a human activity detection and recognition (HADR) task that first detects meaningful motion states and then identifies them. For NP_CMS, we propose a candidate interval generation (detection) and interval-based activity recognition method. On our own dataset, the average recall of candidate interval generation was 95.68%, which means that it provided accurate candidates to the subsequent classifier. The mAP of our method was 87.3%, which indicates that the proposed interval-based activity recognition method was also very powerful. This result is better than the results of two sliding methods (ASSW and FLSW).
Classification-based periodic matching is proposed for detecting and recognizing WP_CMS. The periodic matching method can be used with many classifiers; we experimented with the CNN, SVM, naive Bayes, random forest, and KNN classifiers, and we achieved good results. With periodic matching, the duration of each motion state was accurately segmented and the input to the classifier changed from a signal with a fixed window length to a signal with only one complete period. The experimental results verify that the periodic matching improved the performance of the classifiers.
The experimental results were obtained on two relatively small datasets with few participants. Therefore, the results may be lower on a larger dataset. Moreover, the performance of the proposed methods must be verified in real-time applications and in actual life. Thus, for our next step, we plan to deploy the proposed methods on a smartwatch to evaluate their performance in real-world environments.