Distributed Reliable and Efficient Transmission Task Assignment for WSNs
Abstract
:1. Introduction
- 1)
- A global network view consisting of a multi-level view (including physical topology, routing topology, and task view) is constructed as a conceptual basis for global optimization;
- 2)
- A reliability evaluation model is established from the perspective of the task, and the constraint factors and objective functions of the task allocation are analyzed;
- 3)
- We propose the transmission-oriented reliable and energy-efficient task allocation (TRETA)-Cluster, in which the sink assigns reliability to all cluster heads according to the reliability requirements, and the cluster head performs local task assignment according to the assigned phase target reliability constraints. Simulation results show that TRETA-Cluster reduces the communication cost and latency of task assignment compared to centralized task allocation;
- 4)
- We propose the TRETA-Multi-Sink, where the global view is obtained by fetching local views from multiple sinks. Multiple sinks have a consistent comprehensive view of global optimization. The ways to respond to local task assignment requirements without the need to communicate with remote nodes overcomes the disadvantages of centralized task assignment in large-scale WSNs with significant communication overhead and delay, and have better scalability.
2. Related Work
3. Description of Reliable and Efficient Task Allocation in WSNs
3.1. Energy Consumption Model
3.2. Constraints of Task Reliability and Deadline
3.2.1. Task Deadline Constraint
3.2.2. Task Reliability Constraint
3.3. Reliable and Efficient Task Allocation Problem Model
- Input: , ,
- Output: ,
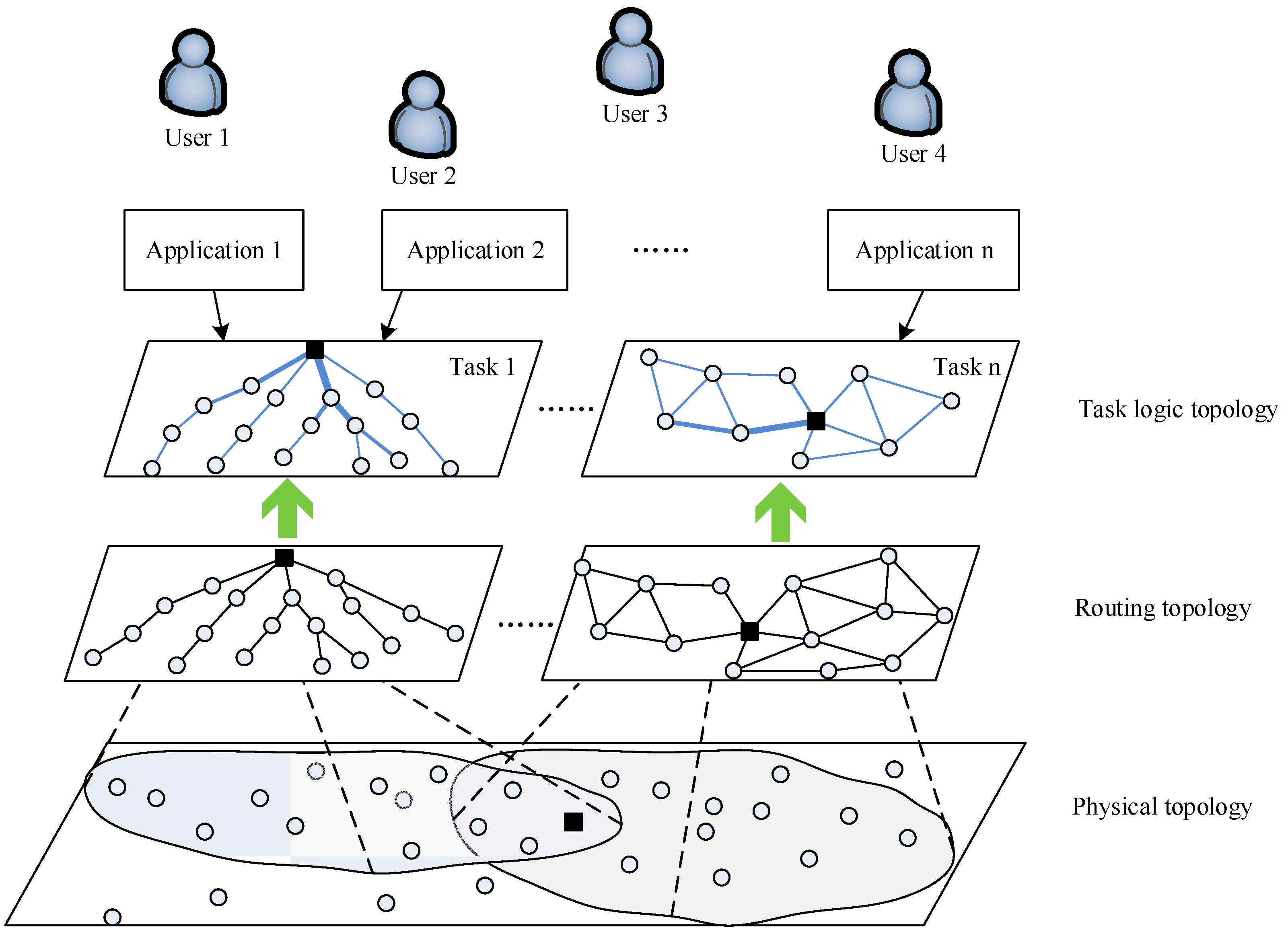
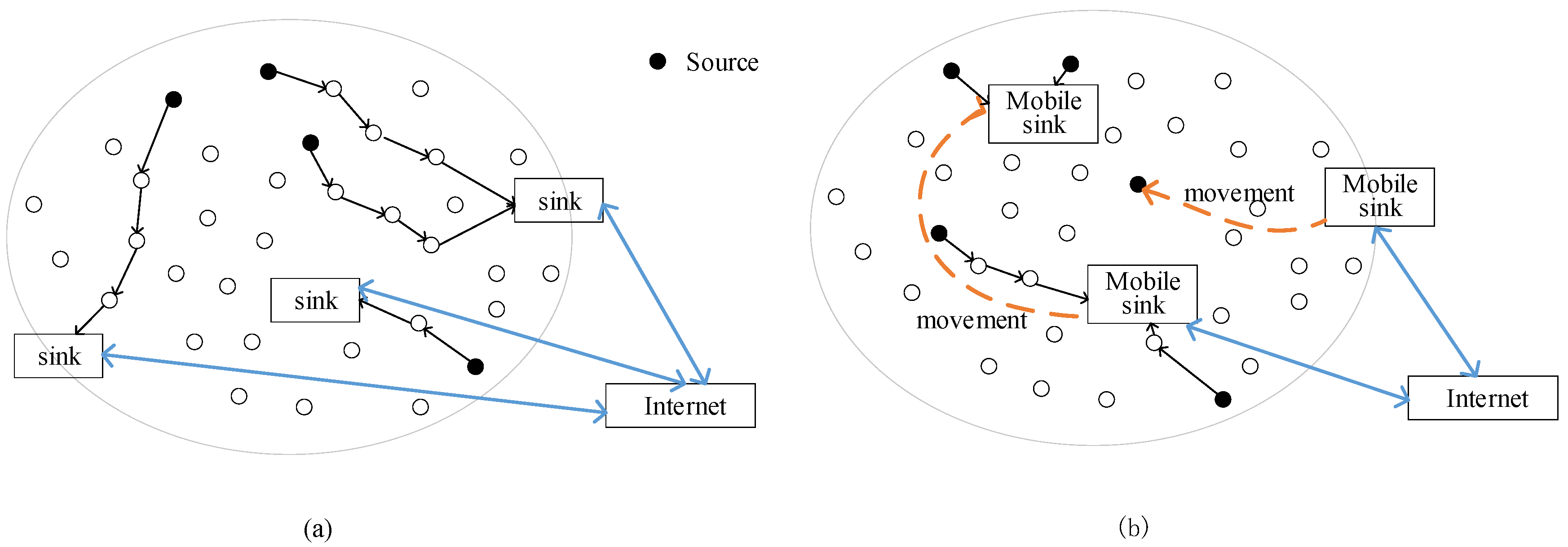
4. Global Network View
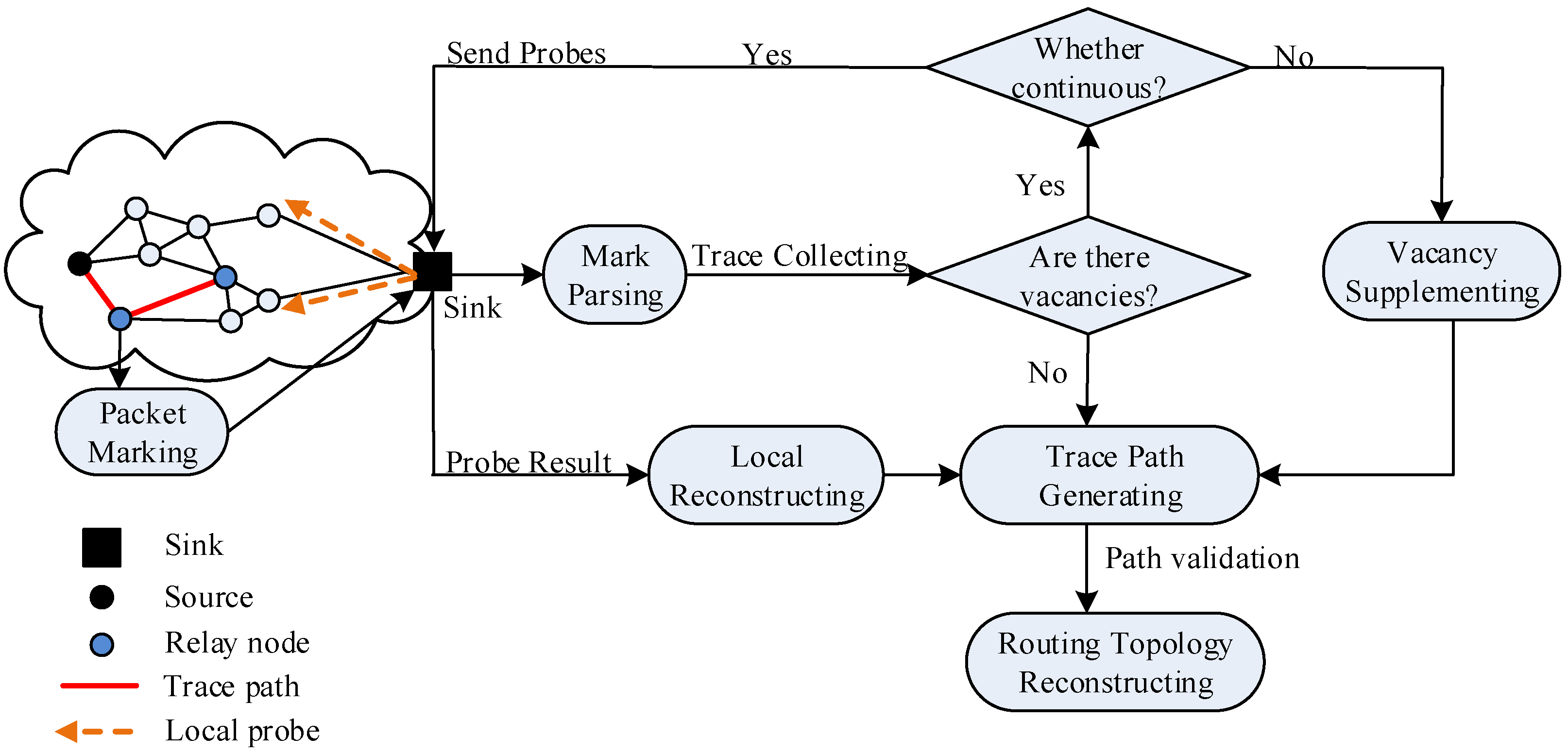
4.1. Route Topology
4.2. Multi-Level Global View
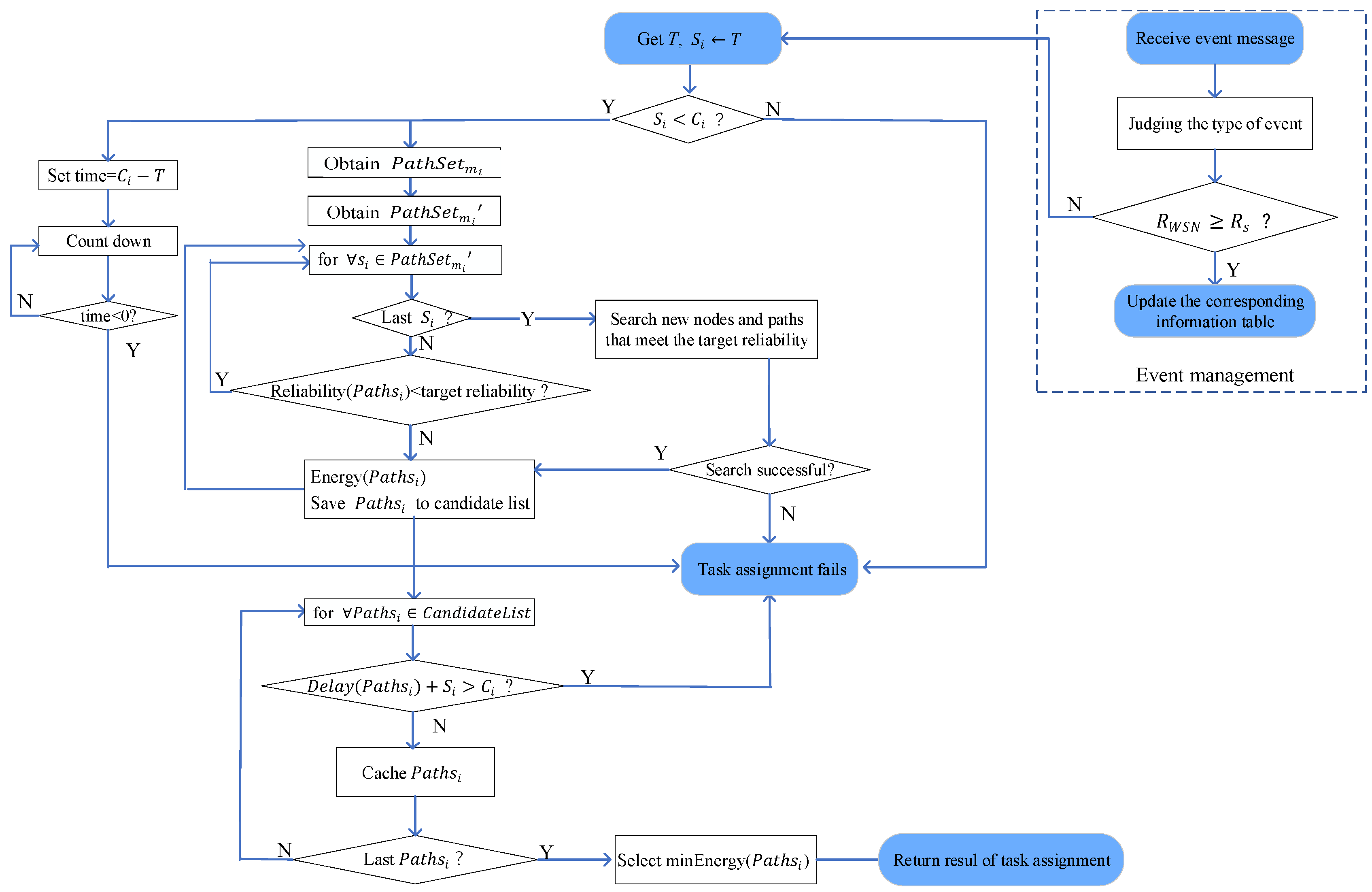
5. Reliable and Efficient Task Allocation Algorithm for WSNs
5.1. Centralized Task Assignment
5.2. Distributed Task Assignment
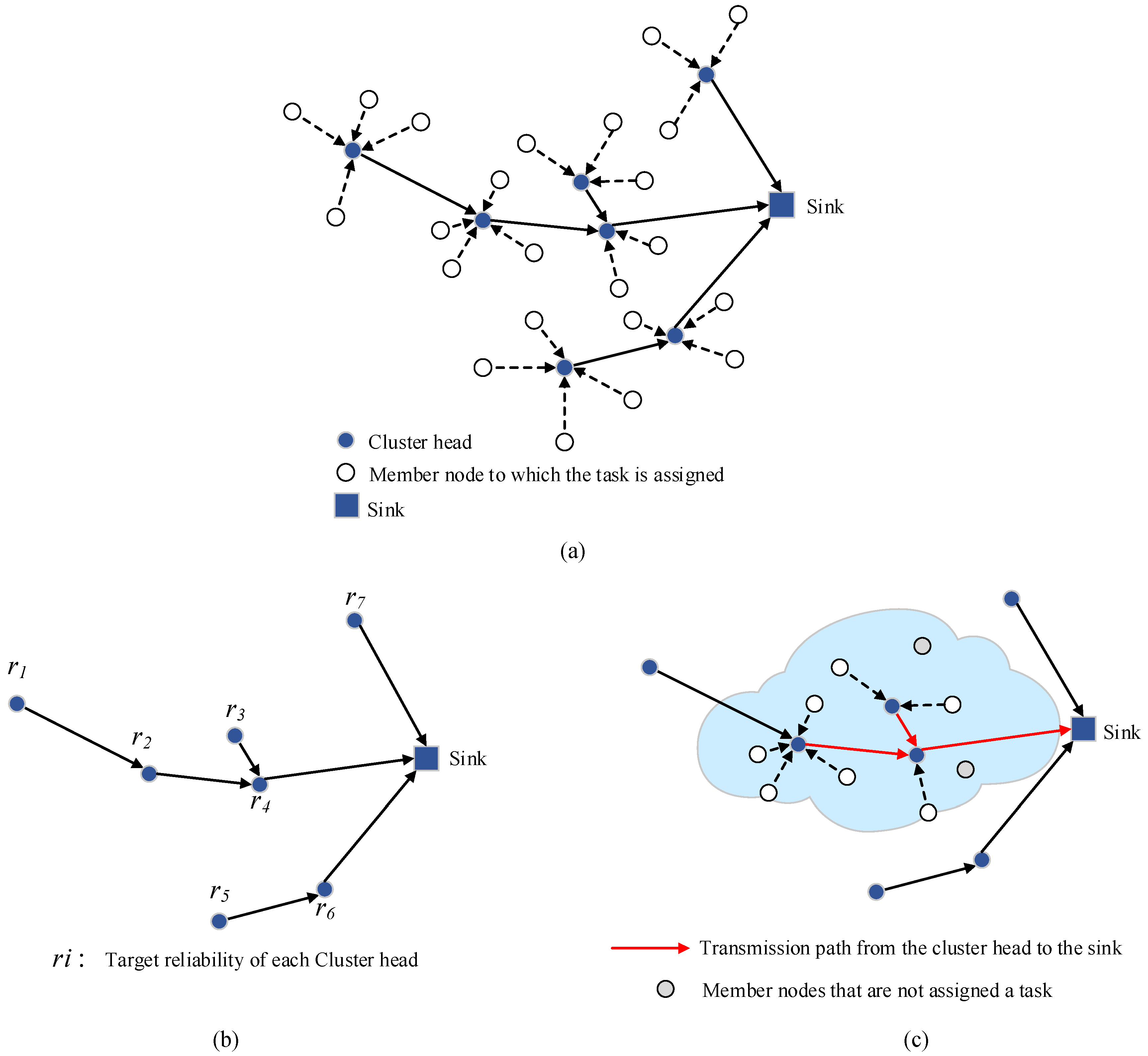
5.2.1. Distributed Reliable and Efficient Task Allocation in a Hierarchical Topology
- 1)
- The sink performs the reliability distribution at the backbone network composed of the cluster heads according to the target reliability, where reliability is obtained at each cluster head, as shown in Figure 4b. Combined with the target reliability and the task deadline constraint, the sink calls the TRETA algorithm to select the cluster head with the smallest total energy consumption that satisfies the task deadline and the target reliability constraint, and the transmission path of the cluster head to the sink.
- 2)
- The cluster head calls the TRETA to select the nodes in the cluster and the intra-cluster paths according to the obtained intra-cluster reliability index and local view to realize the task allocation of the cluster.
| Algorithm 1. TRETA-Cluster |
| Input: Output: |
|
5.2.2. Distributed Reliable and Efficient Task Allocation in Planar Topology
| Algorithm 2. TRETA -Multi-sink |
|
6. Performance Analysis
6.1. Theoretical Analysis
6.1.1. Algorithm Complexity
6.1.2. Communication Load of the Distributed Task Assigned
6.1.3. Delay of Distributed Task Assignment
6.1.4. Energy Resilience of the Transmission in WSNs
6.2. Simulation
6.2.1. Simulation Design
- 1)
- Cluster topologyThe sensing area is 100 m × 100 m, and the number of sensor nodes is 50 to 300. There is only one sink in the cluster topology, with the sink node located in the center of the sensing area and remaining nodes randomly deployed.
- 2)
- Multi-sink-based topologyThe deployment strategies of multiple sinks in a multi-sink-based topology include static and dynamic, random, and scheduled deployment methods. In the proposed simulation experiment, the static uniform deployment method is selected, with the number of sinks set to five, and the sensing area of the square is evenly divided into four sub-areas. One of the five sinks is located in the center of the sensing area, while the remaining four sinks are located in the center of the respective remaining four sub-areas. The five sinks remain fully connected, and the case where the sinks fail is not considered.
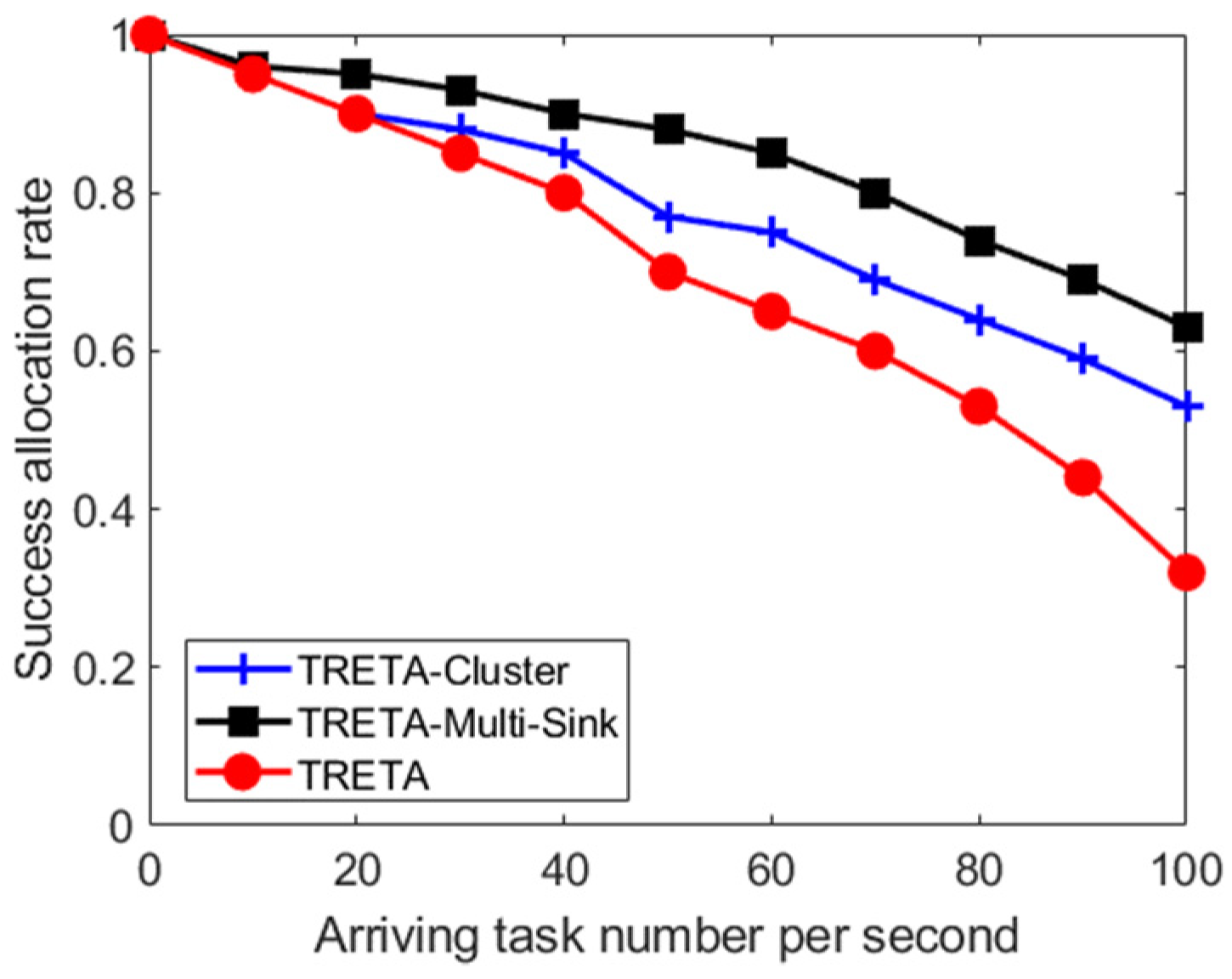
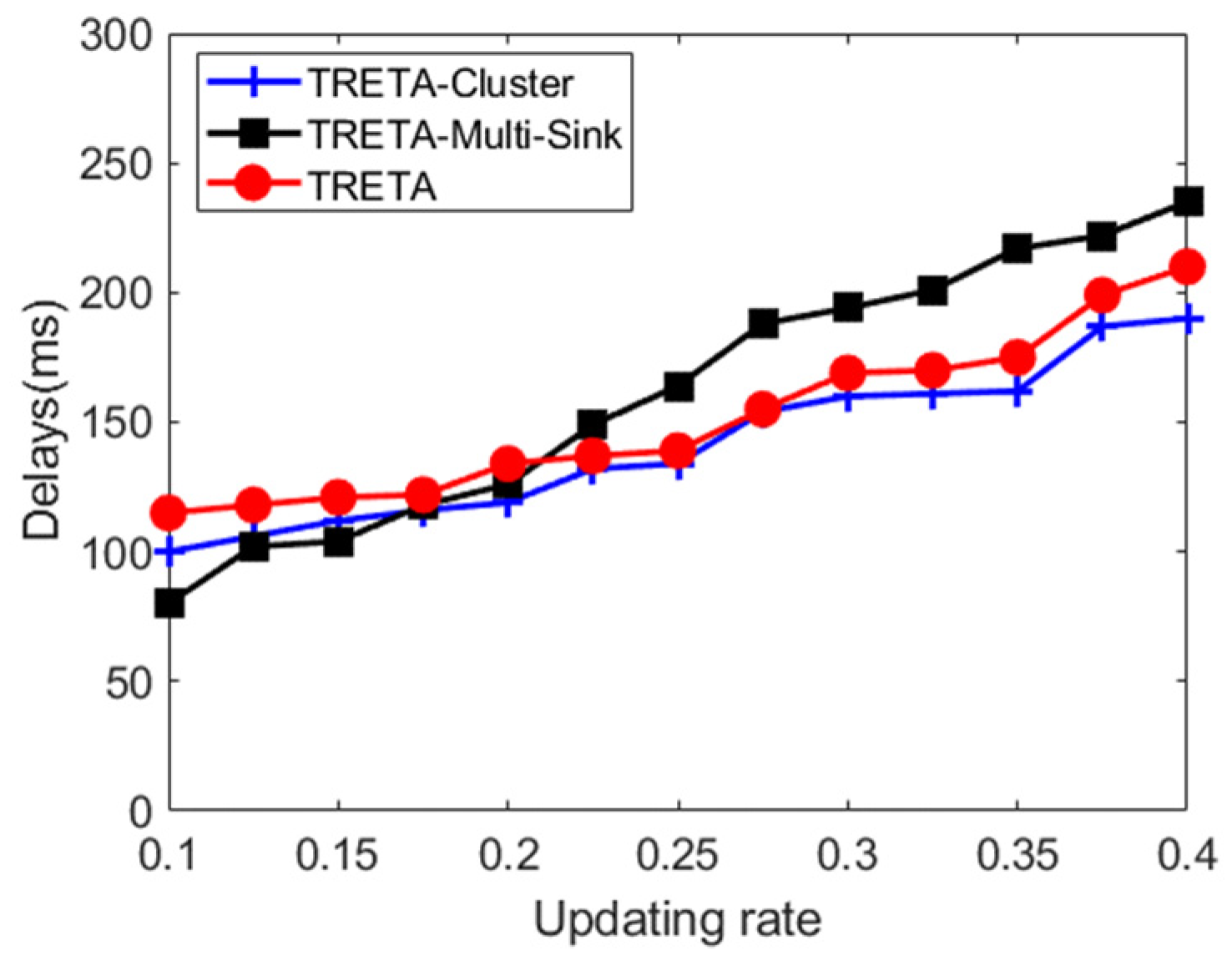
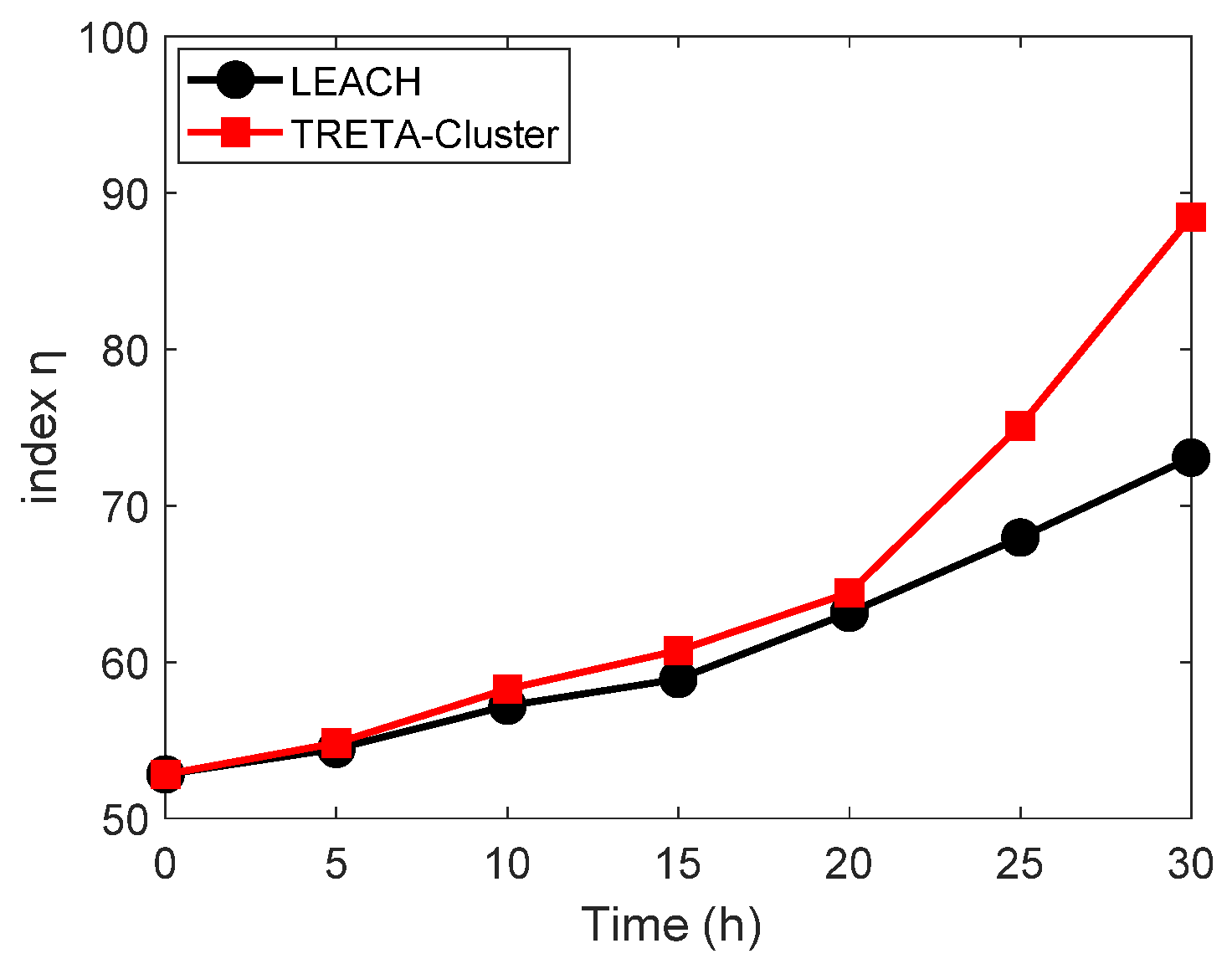
6.2.2. Simulation Results and Analysis
7. Concluding Remarks and Future Work
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Description |
| i-th source node | |
| The task to be assigned, which is the element in the set | |
| Energy consumed by the task on the node | |
| Calculated energy consumption of | |
| Average processing energy consumption of the nodes in the network | |
| Calculation time of the task | |
| Communication energy consumption of the node | |
| Energy consumption of transmitting data of length bit at the distance | |
| Energy consumption of operating the radio model for each bit | |
| Coefficient of the transmit amplifier | |
| Energy consumption of receiving data of length bit at the distance | |
| Task period of | |
| Start time of task | |
| Deadline for task | |
| Mission reliability of the network | |
| Target reliability | |
| i-th transmission Reliability of clustered WSNs from to the sink at time t | |
| Reliability of the i-th transmission performed by cluster c. | |
| Reliability of the head of cluster c which successfully sends the collected data of i-th transmission to sink at time t. | |
| i-th transmission reliability in mesh WSNs from to the sink at time t | |
| Probability that there exists at least one path whose packet delivery rate is greater than the threshold of i-th transmission in the disjoint minimal path sets (from to sink) | |
| i-th transmission reliability in mesh WSNs of j-th path from to the sink at time t | |
| Physical topology of the network | |
| Routing topology of the network | |
| Task set to be assigned at time | |
| Mapped function of | |
| Energy consumption of the task | |
| Physical topology of the backbone network | |
| Routing topology of the backbone network | |
| The physical topology of the intra-cluster | |
| Routing topology of the intra-cluster | |
| Physical topology after backbone network update | |
| Routing topology after backbone network update | |
| Physical topology of the intra-cluster after update | |
| Routing topology of the intra-cluster after update | |
| Local physical topology of the j-th sink in a multi-sink topology | |
| Local routing topology of the j-th sink in a multi-sink topology | |
| The closest sink to the task | |
| Sink adjacent to | |
| Sink involving topology changes | |
| The version ID of the global view | |
| Path set of the source node to the sink in the coverage area of the task | |
| Path set after deleting the paths with link conflict in | |
| Transmission path of each source node to sink in | |
| Reliability of | |
| Energy consumption of | |
| Path to meet the target reliability | |
| Target reliability of cluster head to sink after reliability allocation | |
| Updated | |
| Target reliability of cluster head after reliability allocation | |
| Sink respond to update request of | |
| Routing topology of the j-th sink in | |
| Physical topology of the j-th sink in | |
| Update operation record of | |
| Log of sink which respond to update | |
| Quorum set of writing and reading | |
| Overlapping probability of | |
| Communication load | |
| Number of packets in the allocation policy by multicast, | |
| Communication load for transmitting one global view | |
| Writing load, reading load | |
| Write load of version and update operation of the global view when it is updated | |
| Delay of task assignment for the clustered topology | |
| Delay of the sink allocates a task to the subgraph composed of the cluster heads | |
| Delay of the multicast performed by the sink | |
| Delay in the allocation of the task by the selected cluster head | |
| Delay of TRETA-Multi-Sink | |
| Average of the delays of the tasks assigned by multiple sinks locally | |
| Time to ensure the final consistency of the view | |
| Time of writing the global view whenever it is updated | |
| Time of reading the global view when the distributed task is assigned | |
| Index for energy resilience of the transmission | |
| Number of packet received by the sink after fixed time | |
| Number of initial active nodes | |
| Number of nodes death after a fixed time |
References
- Yu, W.; Huang, Y.; Garcia-Ortiz, A. Distributed optimal on-line task allocation algorithm for wireless sensor networks. IEEE Sens. J. 2018, 18, 446–458. [Google Scholar] [CrossRef]
- Khalil, E.A.; Ozdemir, S.; Tosun, S. Evolutionary task allocation in internet of things-based application domains. Future Gener. Comput. Syst. 2018, 86, 121–133. [Google Scholar] [CrossRef]
- Li, W.; Delicato, F.C.; Pires, P.F.; Lee, Y.C.; Zomaya, A.Y.; Miceli, C.; Pirmez, L. Efficient allocation of resources in multiple heterogeneous wireless sensor networks. J. Parallel Distrib. Comput. 2014, 74, 1775–1788. [Google Scholar] [CrossRef]
- Ghebleh, R.; Ghaffari, A. A multi-criteria method for resource discovery in distributed systems using deductive fuzzy system. Int. J. Fuzzy Syst. 2017, 19, 1829–1839. [Google Scholar] [CrossRef]
- Alskaif, T.; Zapata, M.G.; Bellalta, B. Game theory for energy efficiency in wireless sensor networks: Latest trends. J. Netw. Comput. Appl. 2015, 54, 33–61. [Google Scholar] [CrossRef]
- Pilloni, V.; Navaratnam, P.; Vural, S.; Atzori, L.; Tafazolli, R. Tan: A distributed algorithm for dynamic task assignment in WSNs. IEEE Sens. J. 2014, 14, 1266–1279. [Google Scholar] [CrossRef]
- Tang, C.; Li, X.; Wang, Z.; Han, J. Cooperation and distributed optimization for the unreliable wireless game with indirect reciprocity. Sci. China Inf. Sci. 2018, 60, 110205. [Google Scholar] [CrossRef]
- Duan, X.; Zhao, C.; He, S.; Cheng, P.; Zhang, J. Distributed algorithms to compute Walrasian equilibrium in mobile crowdsensing. IEEE Trans. Ind. Electron. 2017, 64, 4048–4057. [Google Scholar] [CrossRef]
- Pilloni, V.; Atzori, L.; Mallus, M. Dynamic involvement of real-world objects in the IoT: A consensus-based cooperation approach. Sensors 2017, 17, 484. [Google Scholar] [CrossRef]
- Ye, D.Y.; Zhang, M.J.; Vasilakos, A.V. A survey of self-organization mechanisms in multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 441–461. [Google Scholar] [CrossRef]
- Khan, M.I.; Xia, K.; Ali, A.; Aslam, N. Energy-aware task scheduling by a true online reinforcement learning in wireless sensor networks. Int. J. Sens. Netw. 2017, 25, 244–258. [Google Scholar] [CrossRef]
- Nguyen, C.L.; Hoang, D.T.; Wang, P. Data collection and wireless communication in internet of things (IoT) using economic analysis and pricing models: A survey. IEEE Commun. Surv. Tutor. 2016, 18, 2546–2590. [Google Scholar]
- de la Hoz, E.; Gimenez-Guzman, J.; Marsa-Maestre, I.; Orden, D. Automated negotiation for resource assignment in wireless surveillance sensor networks. Sensors 2015, 15, 29547–29568. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wang, Z.; Hu, S.; Liu, L. Ant colony optimization for task allocation in multi-agent systems. China Commun. 2013, 10, 125–132. [Google Scholar] [CrossRef]
- Liu, Q.; Yin, X.; Yang, X.; Ma, Y. Reliability evaluation for wireless sensor networks with chain structures using the universal generating function. Qual. Reliab. Eng. Int. 2017, 33, 2685–2698. [Google Scholar] [CrossRef]
- Cai, J.; Song, X.; Wang, J.; Gu, M. Reliability analysis for a data flow in event-driven wireless sensor networks. Wirel. Pers. Commun. 2014, 78, 151–169. [Google Scholar] [CrossRef]
- He, Y.; Gu, C.; Han, X.; Cui, J.; Chen, Z. Mission reliability modeling for multi-station manufacturing system based on Quality State Task Network. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2017, 231, 701–715. [Google Scholar] [CrossRef]
- Zhu, X.J.; Lu, Y.; Zhang, J.; Wei, Z. Routing topology inference for wireless sensor networks based on packet tracing and local probing. IEICE Trans. Commun. 2019, 102, 122–136. [Google Scholar] [CrossRef]
- Xin, Y.W.; Xiao, Y.W.; Narayanaswamy, B. Reliability allocation model and algorithm for phased mission systems with uncertain component parameters based on importance measure. Reliab. Eng. Syst. Saf. 2018, 180, 266–276. [Google Scholar]
- Garg, H.; Sharma, S.P. Multi-objective reliability-redundancy allocation problem using particle swarm optimization. Comput. Ind. Eng. 2013, 64, 247–255. [Google Scholar] [CrossRef]
- Li, R.; Wang, J.; Liao, H.; Huang, N. A new method for reliability allocation of avionics connected via an airborne network. J. Netw. Comput. Appl. 2015, 48, 14–21. [Google Scholar] [CrossRef]
- Deng, R.; He, S.; Chen, J. An online algorithm for data collection by multiple sinks in wireless sensor networks. IEEE Trans. Control Netw. Syst. 2018, 5, 93–104. [Google Scholar] [CrossRef]
- Basagni, S.; Carosi, A.; Petrioli, C.; Phillips, C.A. Coordinated and controlled mobility of multiple sinks for maximizing the lifetime of wireless sensor networks. Wirel. Netw. 2011, 17, 759–778. [Google Scholar] [CrossRef]
- Lee, E.; Park, S.; Lee, J.; Oh, S.; Kim, S.H. Novel service protocol for supporting remote and mobile users in wireless sensor networks with multiple static sinks. Wirel. Netw. 2011, 17, 861–875. [Google Scholar] [CrossRef]
- Lanny, S.; Kenneth, N.B.; Cormac, J.S. Planning the deployment of multiple sinks and relays in wireless sensor networks. J. Heuristics 2015, 21, 197–232. [Google Scholar]
- Banerjee, A.; Hussain, D.M.A. SD-EAR: Energy aware routing in software defined wireless sensor networks. Appl. Sci. 2018, 8, 1013. [Google Scholar] [CrossRef]
- Gilbert, S.; Lynch, N. Brewer’s conjecture and the feasibility of consistent, available, partition-tolerant web services. Acm Sigact News 2002, 33, 51–59. [Google Scholar] [CrossRef]
- Eventually Consistent-Revisited. Available online: http://www.allthingsdistributed.com/2008/12/eventually_consistent.html (accessed on 4 September 2019).
- DeCandia, G.; Hastorun, D.; Jampani, M.; Kakulapati, G.; Lakshman, A.; Pilchin, A.; Sivasubramanian, S.; Vosshall, P.; Vogels, W. Dynamo: amazon’s highly available key-value store. In ACM SIGOPS Operating Systems Review; ACM: New York, NY, USA, 2007; Volume 41, pp. 205–220. [Google Scholar]
- Vashisht, P.; Sharma, A.; Kumar, R. Strategies for replica consistency in data grid—A comprehensive survey. Concurr. Comput. Pract. Exp. 2018, 29, e3907. [Google Scholar] [CrossRef]
- Wang, X.; Sun, H.; Deng, T. On the tradeoff of availability and consistency for quorum systems in data center networks. Comput. Netw. 2015, 76, 191–206. [Google Scholar] [CrossRef]
- Raychoudhury, V.; Cao, J.; Wu, W. K-directory community: Reliable service discovery in MANET. Pervasive Mob. Comput. 2011, 7, 140–158. [Google Scholar] [CrossRef]
- Guerraoui, R.; Vukolic, M. Refined quorum systems. Distrib. Comput. 2010, 23, 1–42. [Google Scholar] [CrossRef]
- Leccese, F.; Cagnetti, M.; Giarnetti, S.; Petritoli, E.; Luisetto, I.; Tuti, S.; Leccisi, M.; Pecora, A.; Maiolo, L.; Ðurović-Pejčev, R.; et al. Comparison between routing protocols for wide archeological site. In Proceedings of the IEEE International Conference on Metrology for Archaeology and Cultural Heritage, Cassino, Italy, 22–24 October 2018; ISBN 978-1-5386-52. [Google Scholar]



| Parameter | Value |
|---|---|
| Bandwidth | 250 kbps |
| Maximum transmission range of the node | 50 m |
| The initial energy of the node | 2 kJ |
| Parameter | Value |
|---|---|
| Transmission direction | Upstream |
| Task interval | 10 s |
| Task duration | [100 s, 300 s] |
| Target reliability | 90% |
| Packet size | 500 bytes |
| Number of packets per task | [100, 1000] |
| Packet loss rate | 0–10% |
| Topology change rate | 0–10% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Li, K.-C.; Zhang, J.; Zhang, S. Distributed Reliable and Efficient Transmission Task Assignment for WSNs. Sensors 2019, 19, 5028. https://doi.org/10.3390/s19225028
Zhu X, Li K-C, Zhang J, Zhang S. Distributed Reliable and Efficient Transmission Task Assignment for WSNs. Sensors. 2019; 19(22):5028. https://doi.org/10.3390/s19225028
Chicago/Turabian StyleZhu, Xiaojuan, Kuan-Ching Li, Jinwei Zhang, and Shunxiang Zhang. 2019. "Distributed Reliable and Efficient Transmission Task Assignment for WSNs" Sensors 19, no. 22: 5028. https://doi.org/10.3390/s19225028
APA StyleZhu, X., Li, K. -C., Zhang, J., & Zhang, S. (2019). Distributed Reliable and Efficient Transmission Task Assignment for WSNs. Sensors, 19(22), 5028. https://doi.org/10.3390/s19225028






