1. Introduction
SOF-FTIR (Solar Occultation Flux method based on Fourier Transform Infrared spectrometer) method is an optical remote sensing technique for quantifying fugitive VOC emissions from industrial sources. The FTIR is connected to the mobile solar tracker, which reflects the sunlight to the spectrometer. The SOF method can directly measure the wide band absorption spectroscopy of infrared sunlight, as well as the concentration of a gas column integrated along a straight line or surface. Combined with wind measurements, SOF-FTIR has been shown to be very useful to constrain emission of trace gases from source regions [
1]. The SOF method requires very high accuracy in solar tracking. For example, an error smaller than 0.05% in tracking the total gas column is desirable for ground-based solar absorption FTIR to achieve a total CO
2 column precision of 0.1% [
2,
3]. If one wants to maintain this for a tropospheric gas up to a solar zenith angle of 80°, a tracking accuracy of about 19 arc sec is required [
2]. The instrument is placed in a vehicle which is moved across the plume by 60–100 km per hour to obtain the gas emission from a source. The light intensity will change greatly due to cirrus, haze, automobile turning or shade of trees, etc., while the car is moving. In this case, mobile SOF-FTIR is required to track the sun accurately and quickly during movement to satisfy the request of spectral resolution and signal-to-noise ratio. It is a typical high dynamic control system.
Previously, these major efforts were taken to improve the spectrometer itself, but the tracking quality also has to be considered for SOF-FTIR, which is still a key issue. The traditional solar tracking method is mainly based on the camera system to obtain the solar image, and then use image processing technology to extract the solar center point for solar tracking [
4,
5,
6,
7]. However, these methods can only form clear images when the irradiance of the sun is strong enough, and they are easily affected by weather conditions or geographical factors. Moreover, the slow scanning speed of camera and complex image processing algorithm are not suitable for real-time fast-moving solar tracking system.
Fortunately, the position sensitive detector (PSD) provides us with another method of spot location detection. PSD is an analogue optical sensor which consists of a special monolithic PIN photodiode with several electrodes in order to achieve detection in one or two dimensional position detection [
8]. The output of the PSD is a function of the center of gravity of the total light quantity distribution on the active area. PSD has nanoscale position resolution and nanosecond time resolution when measuring the center of gravity of light spots. PSD has a series of advantages over traditional cameras, including fast response time, good positioning accuracy, and simple signal conditioning circuit [
9,
10]. Therefore, PSD has been widely used in a variety of applications, including micro/nano position measurement, vibration detection, tool alignment, aiming and guidance systems, etc., which use lasers or other light sources to directly illuminate the PSD surface for position detection [
9].
Currently, the main challenge of PSD application in different fields is their positioning accuracy, which is mainly affected by circuit noise, tolerances of optical and electronic components, temperature drift of components, the dark current and environment stray light [
11,
12]. These factors seriously affect the resolution and accuracy of the PSD positioning system, which cannot be completely eliminated in the implementation process of the PSD system [
13]. Therefore, many early researches have been carried out on these noise sources and their correction methods [
11,
12,
13,
14,
15]. Study [
11] analyzes the factors that generate substantial errors in the PSD’s response, which are divided into random errors produced by external interference, quantization noise errors produced by A/D conversion, and systematic errors caused by component tolerance and temperature change. The systematic error is source of considerable error that cannot be ignored and must be eliminated. Random errors, which are negligible compared with systematic errors, cannot be eliminated by calibration [
11].
To improve the accuracy of a PSD system, some improved methods have been proposed from the perspective of algorithms or devices. In [
11], the output voltage of four channels of PSD is collected when the infrared light source uniformly illuminates the PSD surface, and then the gain ratio of different channels is fitted by quadratic polynomial mathematical model to correct the circuit gain. This is an effective method to eliminate the effect of amplifying gain imbalance caused by circuit element tolerance. However, it cannot eliminate the effects of dark current and circuit noise, especially when the light source intensity is weak. In [
12], a Kalman filter for the PSD system with laser source is firstly designed for recursively estimating the laser spot position value by linearly modeled from a series of measurements mixed with noises. To further implement the Kalman filter, the system needs to be modeled as accurate as possible. Obviously, this method can roughly correct the position estimation using the detection results, but the system’s measurement errors cannot be calibrated by this method.
The modulation of light source is used to avoid the effects of background light on the premise of stable light intensity [
16,
17]. In [
16], the light intensity of laser diode is modulated with square-wave. The output of PSD can be filtered by a bandpass filter to obtain high SNR and high precision. In [
17], Sinusoidal light intensity modulation and band-pass filtering technology are used to overcome the interference of background light and greatly improve the signal-to-noise ratio (S/N) of position detection system. However, such systems become unfeasible in many normal practical applications due to the need to be compatible with simpler light sources, reduce technical complexity, and reduce system cost [
18]. Thus, a lot of position measurement systems based on PSD with continuous light sources are still produced and utilized in industrial production [
18].
In this area of study, various methods have been adopted to correct distortion. In all cases, Laser Diode or laser-like light sources are often used as matching light source for PSD. The laser diode adapts well to the response wavelength of the PSD because of the high output power and good directivity. The PSD systems constructed with laser diode have better robustness than the continuously changing light source. In this paper, a PSD-based solar spot position detection system is developed for solar tracking closed-loop control of mobile SOF-FTIR. Sunlight is used as matching light source of PSD in the SOF-FTIR system. PSD is required to detect the solar altitude Angle accurately and quickly in dynamic light intensity variation in order to achieve high dynamics and precise loop control. However, the PSD 4-channel gain is always different due to asymmetric circuit parameters, which will introduce PSD incident spot positioning calculation error. In addition, the other major contributor to the positioning error is static output voltage, which is mainly caused by thermal noise, shot noise, and dark current of PSD, especially when the incident light intensity weakens. The purpose of this study is to solve these two problems.
2. Measurement Model and Methods
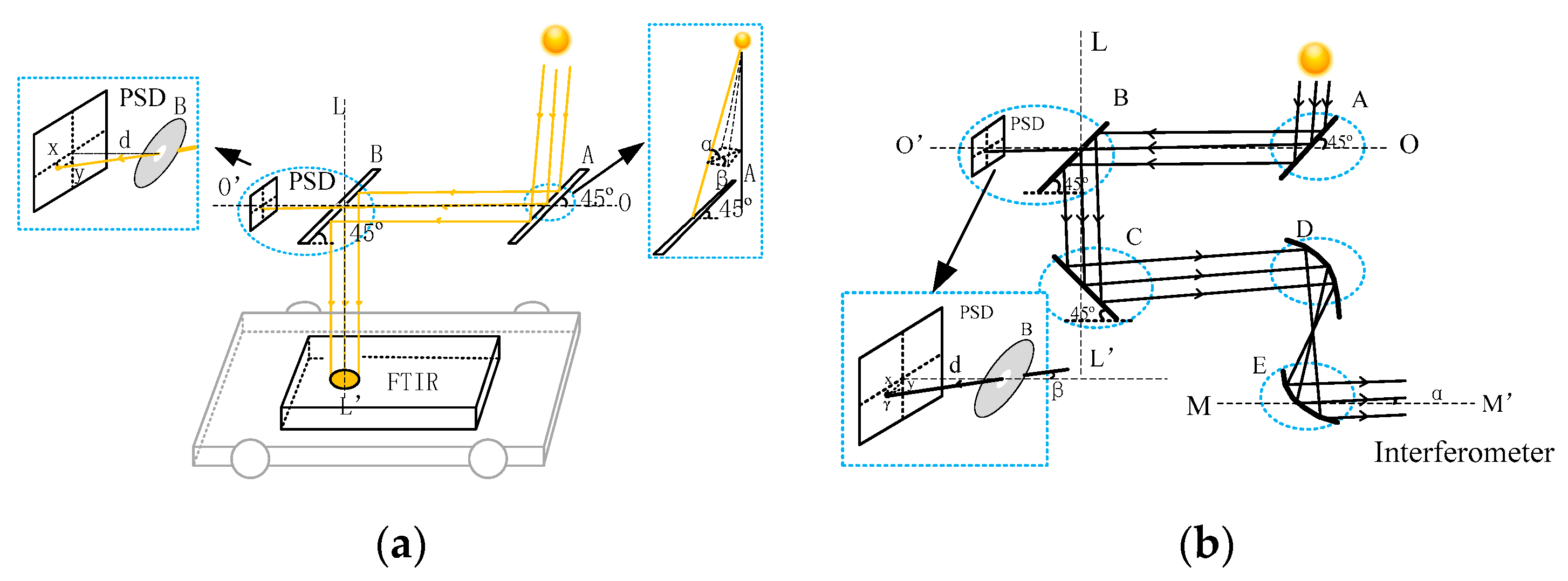
The method adopted in this study is to use PSD to detect the position deviation of the incident point, and then input the PSD signal into the control loop of the tracker for servo control to conduct solar tracking. The schematic diagram of SOF-FTIR is shown in
Figure 1a. The basic structure consists of FTIR spectrometer mounted on a moving vehicle and solar auto-tracking system based on PSD. The latter is an optical system that tracks the sun and reflects the light into the spectrometer independent of its position. The mirrors (A and B) are mounted in parallel. They are at a 45 degree-angle to the
axis and can rotate synchronously along the
axis. Mirror A can rotate along the
axis compared with mirror B. Light beam can reach the PSD surface by opening a hole with
0.5 mm in the center of the mirror B. Subsequently, we can drive mirrors A and B for tracking sun based on X-Y position, which is the point of incidence beam on the PSD surface calculated by the PSD output signal.
The schematic diagram of external light path of FTIR is shown in
Figure 1b. The parameters of FTIR resolution and maximum wave number are as follows,
,
. The maximum divergence Angle
of the beam, entering the interferometer after collimated by the parabolic reflector E, is 6.32 mrad according to the formula
. It is also known that the focal length of parabolic reflectors D and E is 152.4 mm and 100 mm, respectively. The maximum divergence angle of the incident beam to parabolic reflector D is 4.147 mrad (0.2376°) according to the imaging properties of the optical system. The maximum divergence angle β of the solar beam is also 4.147 mrad because the divergence angle of the parallel beam is not affected by the reflection of the plane mirror. According to the angle relation γ = d/tanβ (d = 40 cm), the increment γ of PSD spot displacement is 1.652 mm, which is the maximum acceptable solar tracking error of the system.
As shown in
Figure 2a,b, a template with forty-five 0.5 mm diameter holes is designed to verify the accuracy of spot positioning detection. These holes are distributed on the template evenly. The template and PSD are installed in parallel with a distance of 1 mm, and four sides are exactly aligned through location pins. A power-adjustable laser mounted on a precision three-Axis displacement platform emits parallel beams that shoot directly into the PSD through a template hole. The wavelength of the laser is 600 nm and the spot diameter is
. At different positions, a set of data of each point is acquired continuously by regulating laser power from weak to strong until output voltage saturation. Data is collected and stored in a three-dimensional array DATA[i][j][m] (i = {1,
,45}, j = {1,
,4}, m = {1,
,90}). Here, i represents sample point label, j represents output channel label of each sample point, and m represents the output data number of each channel at different light intensity. This means that 90 pieces of data are collected at per channel at each point. Nine sample points (label i = {1,2,3,20,23,26,43,44,45}) were selected as calibration points on the PSD. Their coordinates are (–4,4),(0,4),(4,4),(–4,0),(0,0),(4,0),(–4,–4),(0,–4),(4,–4), respectively. Other points are used to verify the validity of the calibration method.
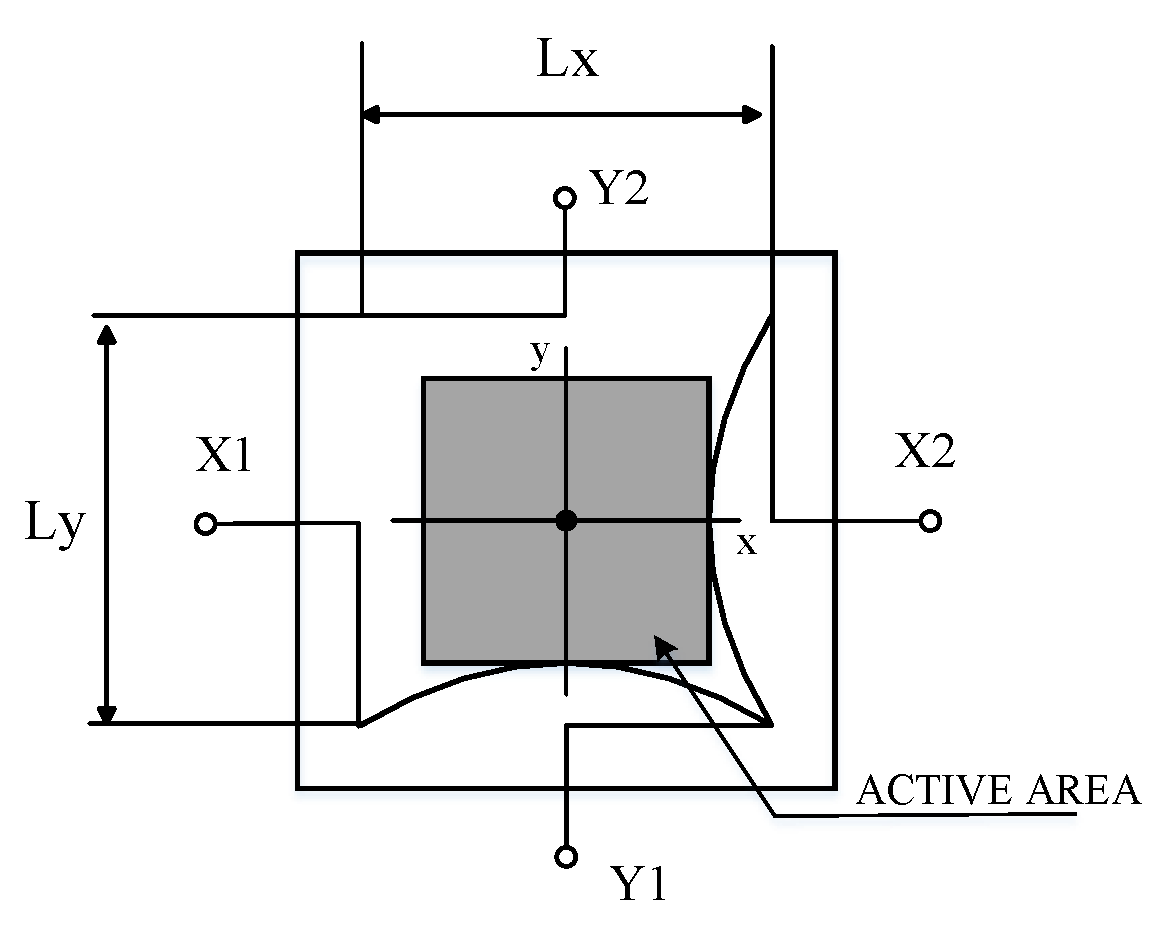
The PSD unit model used in the study is a commercial Hamamatsu S5990-01 with a two dimensional square
sensing area. The photocurrent from four electrodes are divided into 4 parts through the same resistive layer and extracted as position signals. As shown in
Figure 3, the incidence spot position of pin-cushion type PSD are calculated by Equations (1) and (2) [
9].
where Lx, Ly are the sensor dimensions (Lx = Ly = 10 mm), and Ix1, Ix2, Iy1, Iy2 are the currents obtained from PSD electrodes according to the incidence of light, and Io is total photo current expressed as follows, Io = Ix1 + Ix2 + Iy1 + Iy2 [
9].
PSD generates a weak current which is proportional to the level of illumination, and the associated signal conditioning circuitry must be carefully designed to meet the challenges of low bias current, low noise, and high gain [
19]. PSD may either be operated with zero bias (photovoltaic mode) or reverse bias (photoconductive mode). Application of a reverse bias, i.e., operation in the photoconductive mode, can greatly improve both the speed of response and the linearity of the devices [
19]. In the photoconductive mode, a small amount of current called dark current will flow evenly when there is no illumination.
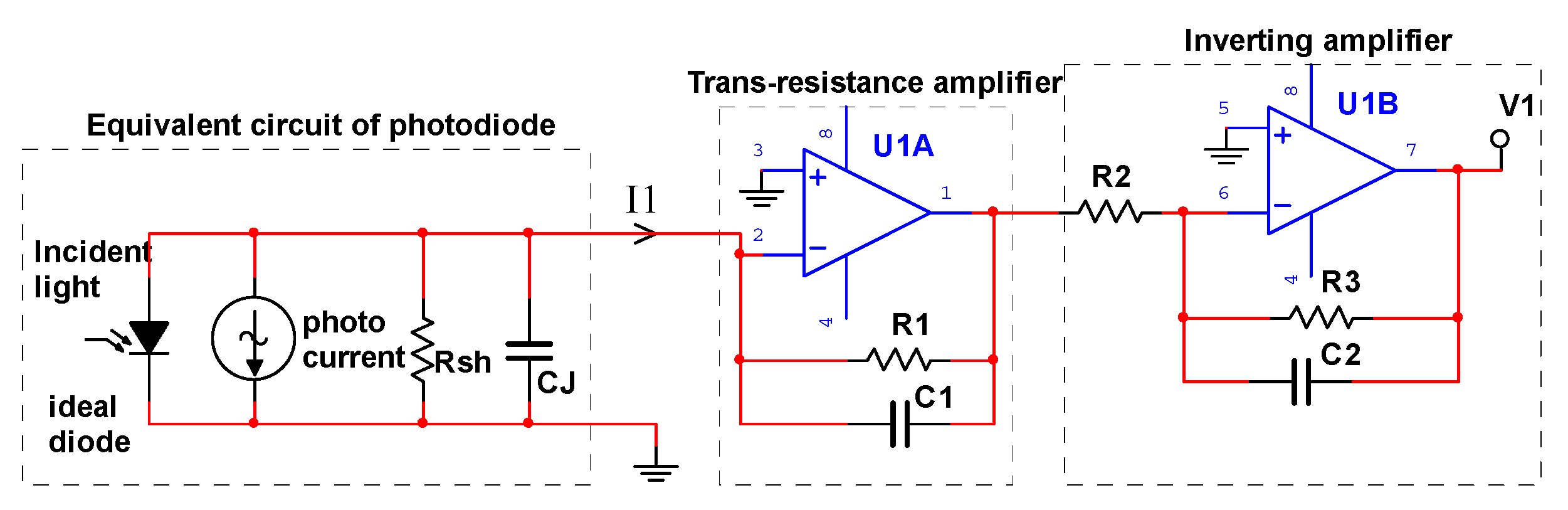
As shown in
Figure 4, PSD signal conditioning circuit mainly contains trans-resistance amplifiers and inverting amplifiers to perform accurate current-to-voltage conversion. The PSD sensor model is S5991-01 produced by Hamamatsu. The PSD is operated in the photoconductive mode for higher switching speeds.
The Four channel output voltage signals (V1, V2, V3, V4) of PSD signal conditioning circuit are proportional to the optical current signal. Ideally, the four signal conditioning circuits have identical parameters. Therefore, the currents (Ix1, Ix2, Iy3, Iy4) can be replaced by voltage (V1, V2, V3, V4) in Equations (1) and (2) [
11].
Ideal trans-resistance gain
is Vi/Ii, for example
is shown in Equation (3).
Equation (4) shows the model of output voltage including component noise (Shot noise, Thermal noise and amplifiers noises), ADC quantization noise, etc.
where k = {1,2,3,4}.
is ideal trans-resistance gain, and
is unbalanced gain coefficient, which are mainly determined by tolerance of circuit components and temperature changes. In fact, four
are always different due to the asymmetry of circuit parameters. A gain equalization correction method based on the origin data is proposed to correct the factor
for eliminating the calculation error of unbalanced gain. In addition, the other major contributor to the positioning error is
, which should be deducted when calculating coordinates.
The equivalent circuit of channel 1 is shown in
Figure 5, and the other three channel circuits are the same as channel 1. Rsh is the interelectrode resistance of PSD. Diode capacitance CJ is a function of junction area and the diode bias voltage.
It is vital for the AC design of signal conditioning circuit to understand the circuit noise gain as a function of frequency, because the noise gain characteristics determine the stability of the circuit [
20]. Noise gain (NG) calculated according to the circuit in
Figure 5 is shown in Equation (5). As per Equation (5), we calculate zero frequency (fz) and pole frequency (fp) of the noise gain transfer function, as shown in Equations (6) and (7). A zero in the noise gain transfer function occurs at a frequency fz, and the pole of the transfer function occurs at a corner frequency fp.
As shown in
Figure 6, the stability of the circuit is determined by the intersecting bode diagram of the amplifier’s open-loop gain and noise gain [
19]. As for unconditional stability, the noise gain curve must intersect the open loop response curve with a net slope less than 20dB per decade, and the circuit phase margin is greater than or equal to 45 degrees [
21]. The noise gain shown in blue dotted line intersects the open loop gain at a net slope of 20 dB per decade, which is regarded as unstable condition. Moreover, it would occur in conditioning circuit if there were no feedback capacitor (i.e., C1 = 0). The noise gain baud diagram (black curve) represents the total noise gain (frequency range) for a given photodiode circuit design. The operational amplifier voltage noise, operational amplifier current noise, and resistance noise will increase the total system noise. However, the operational amplifier voltage noise in the first level is usually the main noise.
The open loop gain (AOL) of operational amplifier (the dotted green line) is the main factor to determine the total bandwidth of a given photodiode circuit design. A faster operational amplifier will move the AOL line to the right, while a slower operational amplifier will move the AOL line to the left. It is important to choose the right operational amplifier for this circuit design. If the operational amplifier is slow, the design will not satisfy the bandwidth and setup time specifications. If the operational amplifier is too fast, the design will generate more noise and have fewer significant digits. The AOL curve can be found in the OP amplifier data sheet.
The input impedance of the circuit caused by CJ will decrease when we increase the frequency from DC. This will increase the noise gain by feeding less output back to the operational amplifier’s inverting input. This process will continue until C1 reaches the same impedance as R1, at which point the black noise gain curve deviates from the dotted blue line. At low frequencies, the noise gain is 1 + R1/Rsh. At high frequencies, it is 1 + CJ/C1. The intersection frequency of noise gain and open-loop gain curve is called closed-loop bandwidth. The red curve determines the maximal noise gain. Moreover, it can be changed by changing parameters of the circuit.