The GA-BPNN-Based Evaluation of Cultivated Land Quality in the PSR Framework Using Gaofen-1 Satellite Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Sample Data
2.3. Satellite Image Data and Preprocessing
2.4. Selecting Satellite-Derived Indicators for CLQ Evaluation
2.5. Modeling and Mapping Methods
2.5.1. Linear Model
2.5.2. Back Propagation Neural Network
2.5.3. Genetic Algorithm-Back Propagation Neural Network
3. Results
3.1. Satellite-Derived Indicators of CLQ Evaluation
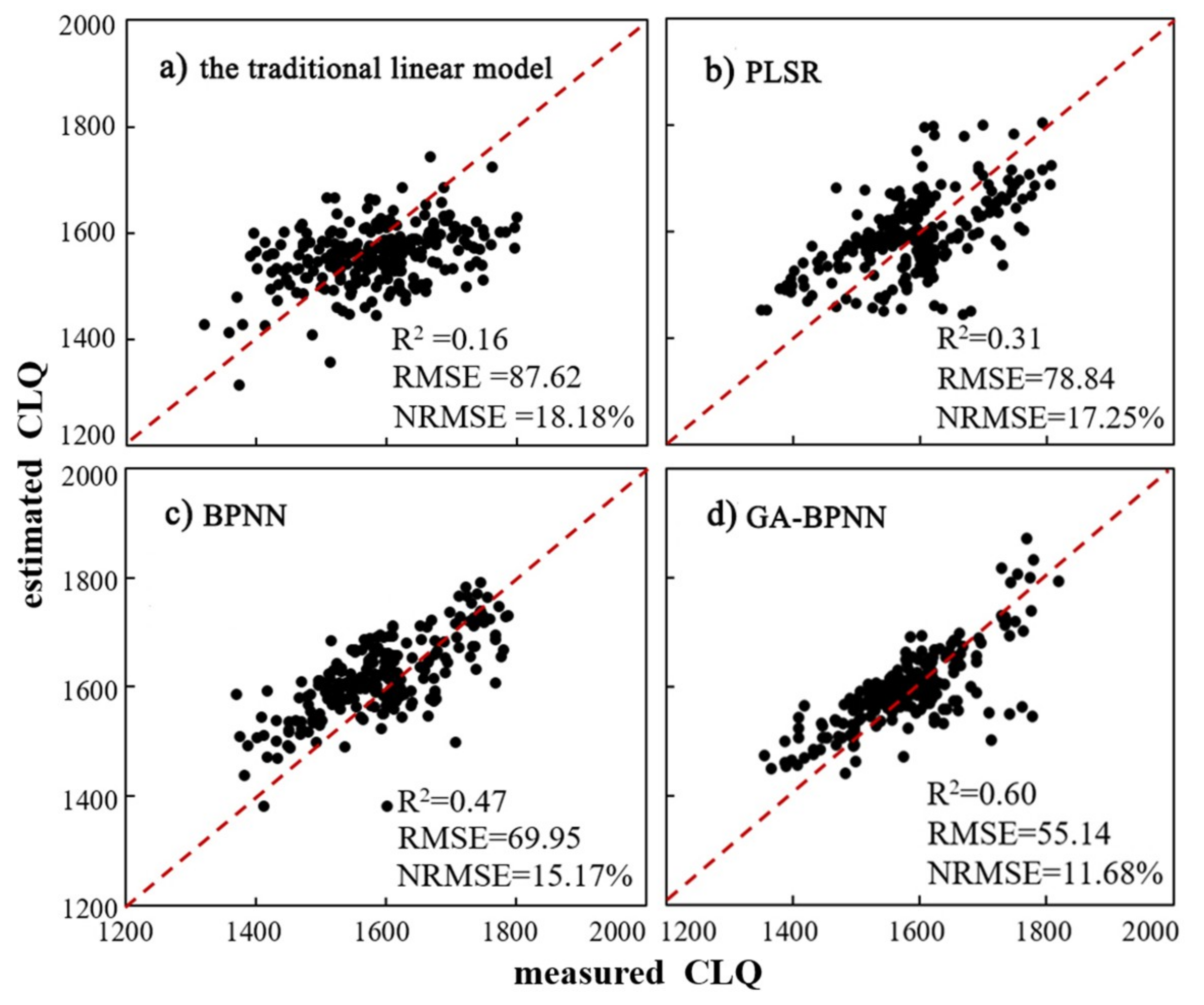
3.2. The Optimal Model for CLQ Evaluation
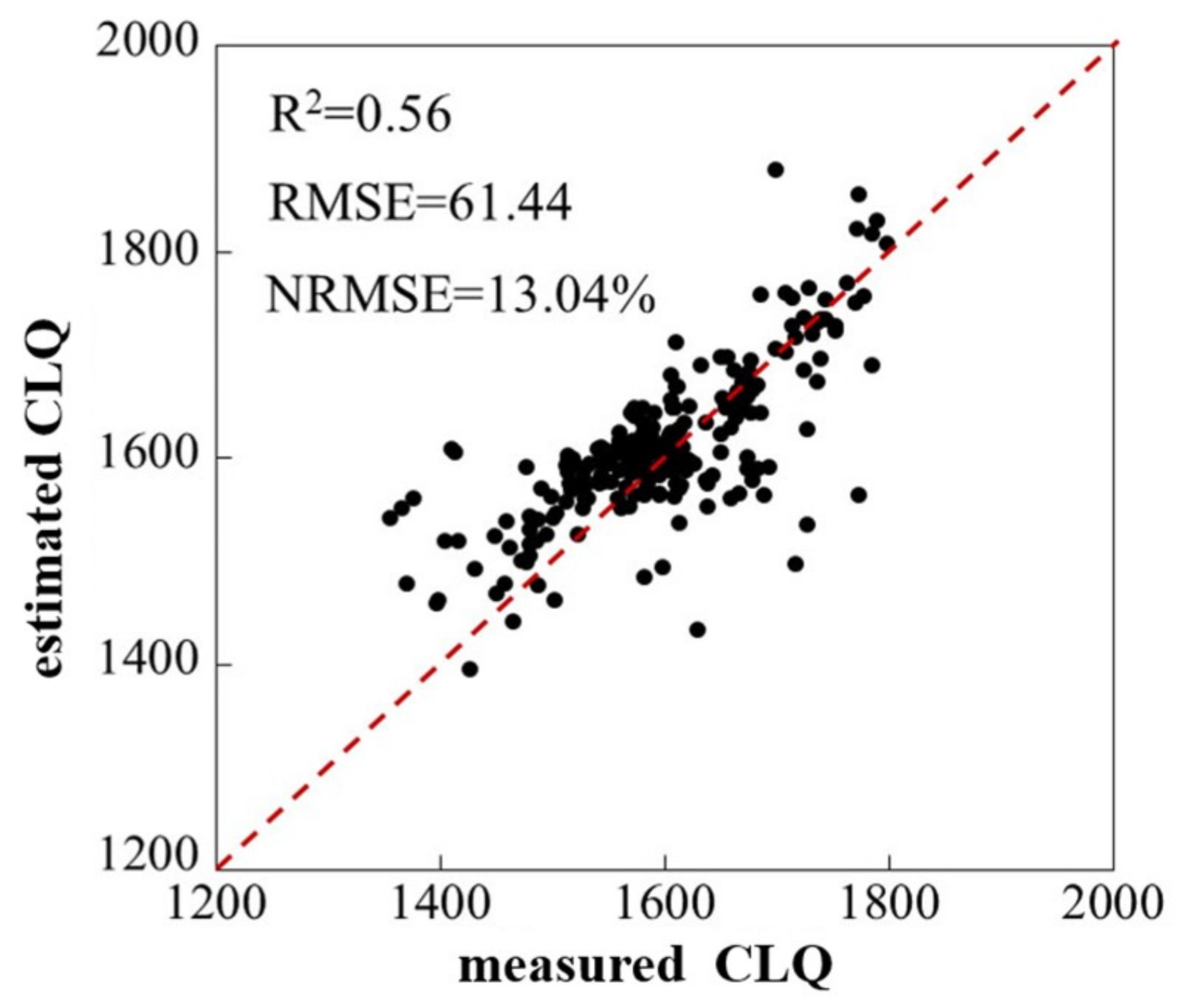
3.3. Spatial Prediction of Cultivated Land Quality at the Regional Scale
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tampakis, S.; Karanikola, P.; Koutroumanidis, T.; Tsitouridou, C. Protecting the productivity of cultivated lands. The viewpoints of farmers in Northern Evros. J. Environ. Prot. Ecol. 2010, 11, 601–613. [Google Scholar]
- Xie, H.L.; Zou, J.L.; Jiang, H.L.; Zhang, N.; Choi, Y. Spatiotemporal pattern and driving forces of arable land-use intensity in China: Toward sustainable land management using emergy analysis. Sustainability 2014, 6, 3504–3520. [Google Scholar] [CrossRef]
- Song, W.; Liu, M.L. Farmland conversion decreases regional and national land quality in China. Land Degrad. Dev. 2017, 28, 459–471. [Google Scholar] [CrossRef]
- German, R.N.; Thompson, C.E.; Benton, T.G. Relationships among multiple aspects of agriculture’s environmental impact and productivity: A meta-analysis to guide sustainable agriculture. Biol. Rev. 2017, 92, 716–738. [Google Scholar] [CrossRef] [PubMed]
- Oliver, M.A.; Gregory, P.J. Soil, food security and human health: A review. Eur. J. Soil Sci. 2015, 66, 257–276. [Google Scholar] [CrossRef]
- Zhu, Q.; Liao, K.H.; Xu, Y.; Yang, G.S.; Wu, S.H.; Zhou, S.L. Monitoring and prediction of soil moisture spatial? temporal variations from a hydropedological perspective: A review. Soil Res. 2012, 50, 625. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.M.; Xu, R.N.; Huang, H.T.; Wu, F. GIS and RS based assessment of cultivated land quality of Shandong Province. Procedia Environ. Sci. 2012, 12, 823–830. [Google Scholar] [CrossRef]
- Liu, Y.S.; Zhang, Y.Y.; Guo, L.Y. Towards realistic assessment of cultivated land quality in an ecologically fragile environment: A satellite imagery-based approach. Appl. Geogr. 2010, 30, 271–281. [Google Scholar] [CrossRef]
- Fang, L.N.; Song, J.P. Cultivated Land Quality Assessment Based on SPOT Multispectral Remote Sensing Image: A Case Study in Jimo City of Shandong Province. Prog. Geogr. 2008, 27, 71–78. [Google Scholar]
- Zhang, Y.Y.; Shi, Y.X.; Wang, J.; Liu, Q.; Fang, L.N. Comprehensive evaluation of cultivated land quality based on RS and PRA: A case study in Hengshan county. Sci. Surv. Mapp. 2008, 33, 133–136. [Google Scholar]
- Yu, X.J. GIS and RS Supported Quantitative Evaluation of Cultivated Land Productivity in Zhaodong City; Northeast Agricultural University: Harbing, China, 2012. [Google Scholar]
- Yang, J.F.; Ma, J.C.; Wang, L.C. Evaluation factors for cultivated land grade identification based on multi-spectral remote sensing. Trans. Chin. Soc. Agric. Eng. 2012, 28, 230–236. [Google Scholar]
- Ye, H.; Ma, Y.; Dong, L.M. Land Ecological Security Assessment for Bai Autonomous Prefecture of Dali Based Using PSR Model-with Data in 2009 as Case. Energy Procedia 2011, 5, 2172–2177. [Google Scholar]
- Bao, S.D. Soil Agricultural Chemistry Analysis; China Agriculture Press: Beijing, China, 2000. [Google Scholar]
- Dumanski, J.; Pieri, C. Land quality indicators: Research plan. Agric. Ecosyst. Environ. 2000, 81, 93–102. [Google Scholar] [CrossRef]
- Al-Kaisi, M.M.; Yin, X.H.; Licht, M.A. Soil carbon and nitrogen changes as influenced by tillage and cropping systems in some Iowa soils. Agr. Ecosyst. Environ. 2005, 105, 635–647. [Google Scholar] [CrossRef]
- Huang, B.; Sun, W.; Zhao, Y.; Zhu, J.; Yang, R.; Zou, Z.; Feng, D.; Jianping, S. Temporal and spatial variability of soil organic matter and total nitrogen in an agricultural ecosystem as affected by farming practices. Geoderma 2007, 139, 336–345. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Li, Z.G.; Wang, Y.L.; Zhou, Q.B.; Wu, J.S.; Peng, J.; Chang, H.F. Spatiotemporal variability of land surface moisture based on vegetation and temperature characteristics in Northern Shaanxi Loess Plateau, China. J. Arid. Environ. 2008, 72, 974–985. [Google Scholar] [CrossRef]
- Heumann, S.; Ringe, H.; Böttcher, J. Long-term net N mineralization potential as an indicator for soil fertility: Chances and constraints. Arch. Agron. Soil Sci. 2012, 58, S107–S111. [Google Scholar] [CrossRef]
- Marti, J.; Bort, J.; Slafer, G.A.; Araus, J.L. Can wheat yield be assessed by early measurements of Normalized Difference Vegetation Index? Ann. Appl. Biol. 2007, 150, 253–257. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, N.B.; Yang, X.H.; Wang, J.H. Study on the interaction between NDVI profile and the growing status of crops. Chin. Geogr. Sci. 2003, 13, 62–65. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Alfredo, R.H.; Kamel, D.; Tomoaki, M. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar]
- Chen, J.M. Evaluation of Vegetation Indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ. 2005, 95, 177–194. [Google Scholar] [CrossRef]
- Yoshino, K.; Ishioka, Y. Guidelines for soil conservation towards integrated basin management for sustainable development: A new approach based on the assessment of soil loss risk using remote sensing and GIS. Paddy Water Environ. 2005, 3, 235–247. [Google Scholar] [CrossRef]
- Han, Y.; Guo, X.; Jiang, Y.F.; Rao, L.; Sun, K.; Yu, H.M. Correlation analysis between cultivated land quality and landscape pattern index in south hilly areas. Jiangsu J. Agric. Sci. 2018, 34, 1057–1065. [Google Scholar]
- Renetzeder, C.; Schindler, S.; Peterseil, J.; Prinz, M.A.; Mücher, S.; Wrbka, T. Can we measure ecological sustainability? Landscape pattern as an indicator for naturalness and land use intensity at regional, national and European level. Ecol. Indic. 2010, 10, 39–48. [Google Scholar] [CrossRef]
- Wang, J.; Wei, C.F.; Liu, W.P.; Zhong, S.Q.; Xing, G.X. A Method for Estimating Quality-Improvement Potential of Cultivated Land in Land Consolidation Projects in Hilly Areas. J. Southwest Univ. 2018, 40, 122–132. [Google Scholar]
- Berg, C.N.; Blankespoor, B.; Selod, H. Roads and Rural Development in Sub-Saharan Africa. J. Dev. Stud. 2018, 54, 856–874. [Google Scholar] [CrossRef]
- Wold, H. Nonlinear Estimation by Iterative Least Squares Procedure. In Research Papers in Statistics; David, F., Ed.; Wiley: Hoboken, NJ, USA, 1966; pp. 441–444. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemometr. Intell. Lab. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Lin, L.X.; Wang, Y.J.; Teng, J.Y.; Xi, X.X. Hyperspectral Analysis of Soil Total Nitrogen in Subsided Land Using the Local Correlation Maximization-Complementary Superiority (LCMCS) Method. Sensors 2015, 15, 17990–18011. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Hu, Y.-M.; Zhou, W.; Liu, Z.-H.; Pan, Y.-C.; Shi, Z.; Wang, L.; Wang, G.-X. Estimation Methods for Soil Mercury Content Using Hyperspectral Remote Sensing. Sustainability 2018, 10, 2474. [Google Scholar] [CrossRef]
- Hively, W.D.; Mccarty, G.W.; Reeves, J.B.; Lang, M.W.; Oesterling, R.A.; Delwiche, S.R. Use of Airborne Hyperspectral Imagery to Map Soil Properties in Tilled Agricultural Fields. Appl. Environ. Soil Sci. 2011, 2011, 1–13. [Google Scholar] [CrossRef]
- Salmerón Gómez, R.; García Pérez, J.; López Martín, M.D.M.; García, C.G. Collinearity diagnostic applied in ridge estimation through the variance inflation factor. J. Appl. Stat. 2016, 43, 1831–1849. [Google Scholar] [CrossRef]
- Saleh, S.; Ibrahim, K.; Eiteba, M.M.; Mohamed, S. Study of genetic algorithm performance through design of multi-step LC compensator for time-varying nonlinear loads. Appl. Soft Comput. 2016, 48, 535–545. [Google Scholar] [CrossRef]
- Peng, Y.P.; Zhao, L.; Hu, Y.M.; Wang, G.X.; Wang, L.; Liu, Z.H. Prediction of Soil Nutrient Contents Using Visible and Near-Infrared Reflectance Spectroscopy. ISPRS Int. J. Geo Inf. 2019, 8, 437. [Google Scholar] [CrossRef]
- Qie, R.Q.; Guan, X.; Yan, X.J.; Dou, S.X.; Zhao, L. Method and its application of natural quality evaluation of arable land based on self-organizing feature map neural network. Trans. Chin. Soc. Agric. Eng. 2014, 30, 298–305. [Google Scholar]
- Khosravi, V.; Ardejani, F.D.; Yousefi, S.; Aryafar, A. Monitoring soil lead and zinc contents via combination of spectroscopy with extreme learning machine and other data mining methods. Geoderma. Int. 2018, 318, 29–41. [Google Scholar] [CrossRef]
- Wang, W.; Yu, B. Text categorization based on combination of modified back propagation neural network and latent semantic analysis. Neural Comput. Appl. 2008, 18, 875–881. [Google Scholar] [CrossRef]



| Satellite | Parameter Value | Bands | ||||
|---|---|---|---|---|---|---|
| Band 1 | Band 2 | Band 3 | Band 4 | Band 6 | ||
| GF-1 | Gain | 0.2072 | 0.1776 | 0.1770 | 0.1909 | |
| Landsat-8 TRIS | Bias | 7.5348 | 3.9395 | −1.7445 | −7.2053 | |
| Gain | 1.1807 | 1.2098 | 0.9425 | 0.9692 | 17.04 | |
| Bias | −7.3800 | −7.6100 | −5.9400 | −6.0700 | 12.65 | |
| Target Layer | Project Layer | Satellite-Derived Indicator Layer |
|---|---|---|
| CLQ evaluation indicator system | Pressure Resistance Index (PRI) | Slope |
| Land State Index (LSI) | TVDI | |
| VIs | ||
| Land Use Response Index (LURI) | RA | |
| PFD |
| VIs | Algorithm Formula | Reference |
|---|---|---|
| NDVI | [21,22] | |
| EVI | [23] | |
| MSAVI | [24] | |
| SAVI | [25] | |
| PVI | (a=0.9, b=0.1) | [26,27] |
| Soil Fertility Parameters | NDVI | EVI | MSAVI | SAVI | PVI |
|---|---|---|---|---|---|
| SOM (%) | 0.82 ** | 0.88 ** | 0.87 ** | 0.84 ** | 0.85 ** |
| TN (mg/kg) | 0.75 ** | 0.90 ** | 0.88 ** | 0.78 ** | 0.79 ** |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Peng, Y.; Xia, Z.; Hu, Y.; Wang, G.; Zhu, A.-X.; Liu, Z. The GA-BPNN-Based Evaluation of Cultivated Land Quality in the PSR Framework Using Gaofen-1 Satellite Data. Sensors 2019, 19, 5127. https://doi.org/10.3390/s19235127
Liu S, Peng Y, Xia Z, Hu Y, Wang G, Zhu A-X, Liu Z. The GA-BPNN-Based Evaluation of Cultivated Land Quality in the PSR Framework Using Gaofen-1 Satellite Data. Sensors. 2019; 19(23):5127. https://doi.org/10.3390/s19235127
Chicago/Turabian StyleLiu, Shanshan, Yiping Peng, Ziqing Xia, Yueming Hu, Guangxing Wang, A-Xing Zhu, and Zhenhua Liu. 2019. "The GA-BPNN-Based Evaluation of Cultivated Land Quality in the PSR Framework Using Gaofen-1 Satellite Data" Sensors 19, no. 23: 5127. https://doi.org/10.3390/s19235127
APA StyleLiu, S., Peng, Y., Xia, Z., Hu, Y., Wang, G., Zhu, A.-X., & Liu, Z. (2019). The GA-BPNN-Based Evaluation of Cultivated Land Quality in the PSR Framework Using Gaofen-1 Satellite Data. Sensors, 19(23), 5127. https://doi.org/10.3390/s19235127






