A Clamping Force Estimation Method Based on a Joint Torque Disturbance Observer Using PSO-BPNN for Cable-Driven Surgical Robot End-Effectors
Abstract
1. Introduction
2. Methods
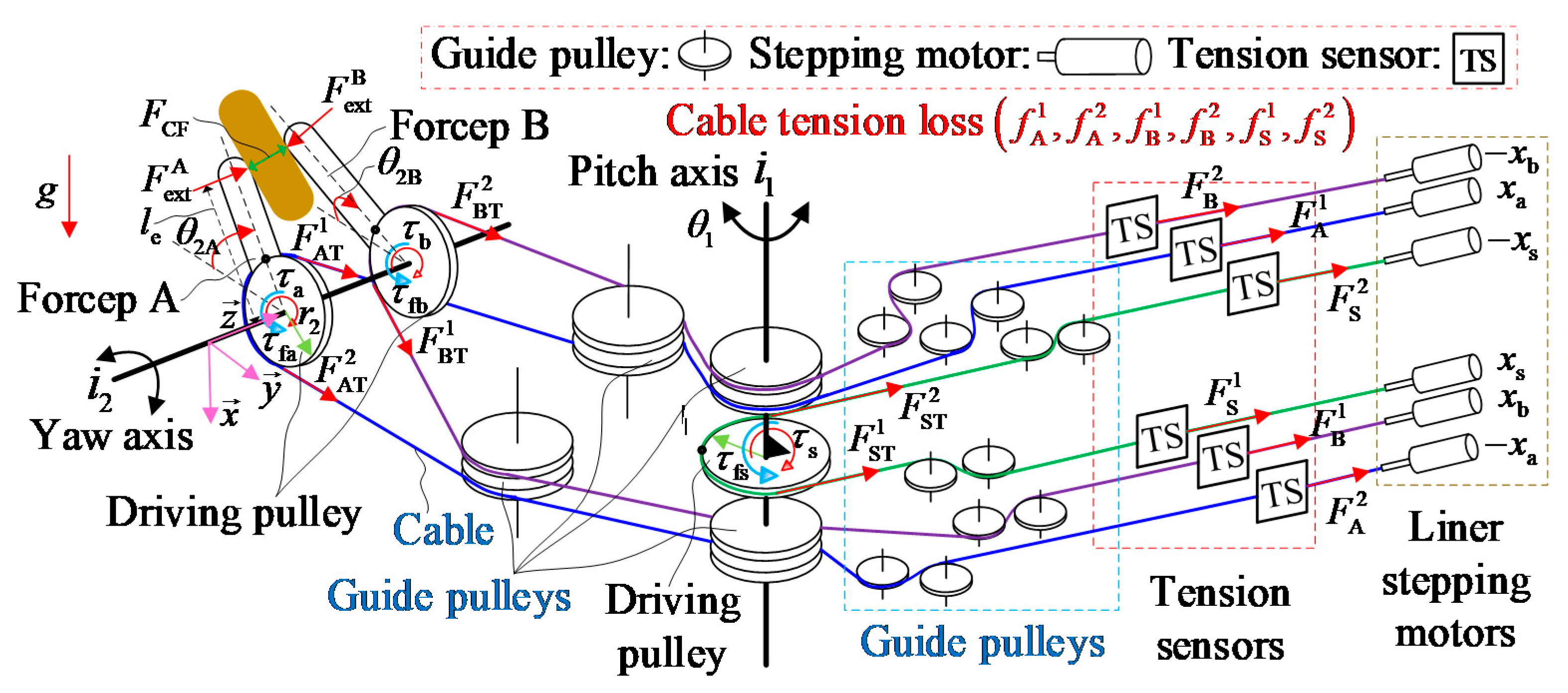
2.1. Description of the 3-Degrees of Freedom (3-DoF) Cable-Driven Surgical Robot End-Effector
2.2. Equivalent Experimental System for the Surgical Robot End-Effector
2.3. Strategy for Estimating the Clamping Force of the Surgical Robot End-Effector
2.3.1. Modeling the System Dynamics of the Forceps
2.3.2. Strategy for Estimating the Clamping Force
2.3.3. Joint Torque Disturbance Observer Using PSO-BPNN
- (a)
- Determine the topological structure of the BP neural network and set the number of neurons in each layer of the BP neural network. The particle population is initialized, and the velocity and position of each particle are randomly set. The main operating parameters of particle swarm optimization are shown in Table 1.
- (b)
- Calculate the fitness value Fit (i) of each particle;
- (c)
- Compare the fitness value Fit (i) of each particle with the individual extreme value. If Fit (i) > pbest (i), replace pbest (i) with Fit (i).
- (d)
- Compare the fitness value Fit (i) of each particle with the global extreme value gbest (i). If Fit (i) > gbest (i), replace gbest (i) with Fit (i).
- (e)
- Update the position and velocity of each particle according to Equation (18);
- (f)
- If the condition is satisfied (the error is sufficiently small or the number of cycles has reached its maximum), exit; otherwise, return to the second step (b);
- (g)
- The global extreme value gbest (i) from the PSO algorithm is used as the weight and threshold for the BP neural network and to train the neural network with training samples;
- (h)
- The generalization ability of the PSO-BPNN can be tested by simulation with the test samples.
2.3.4. The Clamping Force Estimator
3. Results and Discussion
3.1. Training and Testing Results from the Cable Tension Estimation Model Based on the PSO-BPNN under Free Motion
3.2. Experimental Results of Clamping Force Estimation
3.3. Analysis and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Marcus, H.; Nandi, D.; Darzi, A.; Yang, G. Surgical Robotics Through a Keyhole: From Today’s Translational Barriers to Tomorrow’s ‘Disappearing’ Robots. IEEE Trans. Bio-Med. Eng. 2013, 60, 674–681. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zi, B.; Ding, H.; You, W.; Yu, L. Hybrid grey prediction model-based autotracking algorithm for the laparoscopic visual window of surgical robot. Mech. Mach. Theory 2018, 123, 107–123. [Google Scholar] [CrossRef]
- Mohareri, O.; Ramezani, M.; Adebar, T.; Abolmaesumi, P.; Salcudean, S. Automatic Localization of the da Vinci Surgical Instrument Tips in 3-D Transrectal Ultrasound. IEEE Trans. Bio-Med. Eng. 2013, 60, 2663–2672. [Google Scholar] [CrossRef] [PubMed]
- Blake, H.; Jacob, R.; Diana, W.; King, H.; Roan, P.; Cheng, L.; Glozman, D.; Ma, J.; Kosari, S.; White, L. Raven-II: An Open Platform for Surgical Robotics Research. IEEE Trans. Bio-Med. Eng. 2013, 60, 954–959. [Google Scholar]
- Hagn, U.; Nickl, M.; Jörg, S.; Passig, G.; Bahls, T.; Nothhelfer, A.; Hacker, F.; Le-Tien, L.; Albu-Schäffer, A.; Konietschke, R.; et al. The DLR MIRO: A versatile lightweight robot for surgical applications. Ind. Robot 2008, 35, 324–336. [Google Scholar] [CrossRef]
- Kim, U.; Lee, D.H.; Yoon, W.J.; Hannaford, B.; Choi, H.R. Force sensor integrated surgical forceps for minimally invasive robotic surgery. IEEE Trans. Robot. 2015, 31, 1214–1224. [Google Scholar] [CrossRef]
- Gonenc, B.; Chamani, A.; Handa, J.; Gehlbach, P.; Taylor, R.; Iordachita, I. 3-DOF Force-Sensing Motorized Micro-Forceps for Robot-Assisted Vitreoretinal Surgery. IEEE Sens. J. 2017, 17, 3526–3541. [Google Scholar] [CrossRef]
- Aviles, A.; Alsaleh, S.; Hahn, J.; Casals, A. Towards retrieving force feedback in robotic-assisted surgery: A supervised neuro-recurrent-vision approach. IEEE Trans. Haptics 2016, 10, 431–443. [Google Scholar] [CrossRef]
- Wang, Z.; Zi, B.; Wang, D.; Qian, J.; You, W.; Yu, L. External force self-sensing based on cable-tension disturbance observer for surgical instrument. IEEE Sens. J. 2019, 19, 5274–5284. [Google Scholar] [CrossRef]
- Chen, B.; Zi, B.; Wang, Z.; Qin, L.; Liao, W. Knee exoskeletons for gait rehabilitation and human performance augmentation: A state-of-the-art. Mech. Mach. Theory 2019, 134, 499–511. [Google Scholar] [CrossRef]
- Chen, Q.; Zi, B.; Sun, Z.; Li, Y.; Xu, Q. Design and Development of a New Cable-Driven Parallel Robot for Waist Rehabilitation. IEEE/ASME Trans. Mech. 2019, 24, 1497–1507. [Google Scholar] [CrossRef]
- Wu, L.; Crawford, R.; Roberts, J. Dexterity analysis of three 6-DOF continuum robots combining concentric tube mechanisms and cable-driven mechanisms. IEEE Robot. Autom. Lett. 2016, 2, 514–521. [Google Scholar] [CrossRef]
- Hwang, M.; Kwon, D.S. Strong continuum manipulator for flexible endoscopic surgery. IEEE/ASME Trans. Mech. 2019, 24, 2193–2203. [Google Scholar] [CrossRef]
- Ma, X.; Song, C.; Chiu, P.W.; Li, Z. Autonomous Flexible Endoscope for Minimally Invasive Surgery with Enhanced Safety. IEEE Robot. Autom. Lett. 2019, 4, 2607–2613. [Google Scholar] [CrossRef]
- Kuebler, B.; Seibold, U.; Hirzinger, G. Development of actuated and sensor integrated forceps for minimally invasive surgery. Int. J. Med. Robot. Comp. 2006, 1, 96–107. [Google Scholar] [CrossRef] [PubMed]
- Trejos, A.; Escoto, A.; Naish, M.; Patel, R. Design and Evaluation of a Sterilizable Force Sensing Instrument for Minimally Invasive Surgery. IEEE Sens. J. 2017, 17, 3983–3993. [Google Scholar] [CrossRef]
- Yu, L.; Yan, Y.; Yu, X.; Xia, Y. Design and Realization of Forceps With 3-D Force Sensing Capability for Robot-Assisted Surgical System. IEEE Sens. J. 2018, 18, 8924–8932. [Google Scholar] [CrossRef]
- Li, K.; Pan, B.; Zhan, J.; Gao, W.; Fu, Y.; Wang, S. Design and performance evaluation of a 3-axis force sensor for MIS palpation. Sens. Rev. 2015, 35, 219–228. [Google Scholar] [CrossRef]
- Yu, H.; Jiang, J.; Xie, L.; Liu, L.; Shi, Y.; Cai, P. Design and static calibration of a six-dimensional force/torque sensor for minimally invasive surgery. Minim. Invasive Ther. Allied Technol. 2014, 23, 136–143. [Google Scholar] [CrossRef]
- Lim, S.; Lee, H.; Park, J. Grip force measurement of forceps with fibre Bragg grating sensors. Electron. Lett. 2014, 50, 733–735. [Google Scholar] [CrossRef]
- Kim, U.; Lee, D.; Kim, Y.; Seok, D.Y.; So, J.; Choi, H. S-surge: Novel portable surgical robot with multiaxis force-sensing capability for minimally invasive surgery. IEEE/ASME Trans. Mech. 2017, 22, 1717–1727. [Google Scholar] [CrossRef]
- Kim, U.; Kim, Y.B.; So, J.; Seok, D.Y.; Choi, H.R. Sensorized surgical forceps for robotic-assisted minimally invasive surgery. IEEE Trans. Ind. Electron. 2018, 65, 9604–9613. [Google Scholar] [CrossRef]
- Radó, J.; Dücső, C.; Földesy, P.; Szebényi, G.; Nawrat, Z.; Rohr, K.; Fürjes, P. 3D force sensors for laparoscopic surgery tool. Microsyst. Technol. 2018, 24, 519–525. [Google Scholar] [CrossRef]
- Overtoom, E.; Horeman, T.; Jansen, F.; Dankelman, J.; Schreuder, H. Haptic feedback, force feedback, and force-sensing in simulation training for laparoscopy: A systematic overview. J. Surg. Educ. 2019, 76, 242–261. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Nelson, C. Estimating Tool-Tissue Forces Using a 3-Degree-of-Freedom Robotic Surgical Tool. J. Mech. Robot. 2016, 8, 051015. [Google Scholar] [CrossRef]
- Li, H.; Kawashima, K.; Tadano, K.; Ganguly, S.; Nakano, S. Achieving haptic perception in forceps’ manipulator using pneumatic artificial muscle. IEEE/ASME Trans. Mech. 2013, 18, 74–85. [Google Scholar] [CrossRef]
- Haraguchi, D.; Kanno, T.; Tadano, K.; Kawashima, K. A pneumatically driven surgical manipulator with a flexible distal joint capable of force sensing. IEEE/ASME Trans. Mech. 2015, 20, 2950–2961. [Google Scholar] [CrossRef]
- Xue, R.; Ren, B.; Huang, J.; Yan, Z.; Du, Z. Design and Evaluation of FBG-Based Tension Sensor in Laparoscope Surgical Robots. Sensors 2018, 18, 2067. [Google Scholar] [CrossRef]
- Xue, R.; Du, Z.; Yan, Z.; Ren, B. An estimation method of grasping force for laparoscope surgical robot based on the model of a cable-pulley system. Mech. Mach. Theory 2019, 134, 440–454. [Google Scholar] [CrossRef]
- Li, Y.; Hannaford, B. Gaussian process regression for sensorless grip force estimation of cable-driven elongated surgical instruments. IEEE Robot. Autom. Lett. 2017, 2, 1312–1319. [Google Scholar] [CrossRef]
- Liang, Y.; Du, Z.; Wang, W.; Yan, Z.; Sun, L. An improved scheme for eliminating the coupled motion of surgical instruments used in laparoscopic surgical robots. Robot. Auton. Syst. 2019, 112, 49–59. [Google Scholar] [CrossRef]
- Gessert, N.; Beringhoff, J.; Otte, C.; Schlaefer, A. Force estimation from OCT volumes using 3D CNNs. Int. J. Comput. Ass. Rad. 2018, 13, 1073–1082. [Google Scholar] [CrossRef]
- Li, X.; Cao, L.; Tiong, A.; Phan, P.; Phee, S. Distal-end force prediction of tendon-sheath mechanisms for flexible endoscopic surgical robots using deep learning. Mech. Mach. Theory 2019, 134, 323–337. [Google Scholar] [CrossRef]
- Yu, L.; Wang, W.; Zhang, F. External force sensing based on cable tension changes in minimally invasive surgical micromanipulators. IEEE Access 2018, 6, 5362–5373. [Google Scholar] [CrossRef]
- Hwang, W.; Lim, S.C. Inferring Interaction Force from Visual Information without Using Physical Force Sensors. Sensors 2017, 17, 2455. [Google Scholar] [CrossRef]
- Huang, J.; Yan, Z.; Xue, R. Grip Force Estimation of Laparoscope Surgical Robot based on Neural Network Optimized by Genetic Algorithm. In Proceedings of the 3rd International Conference on Robotics, Control and Automation, Chengdu, China, 11–13 August 2018; pp. 95–100. [Google Scholar]
- Marban, A.; Srinivasan, V.; Samek, W.; Fernández, J.; Casals, A. A recurrent convolutional neural network approach for sensorless force estimation in robotic surgery. Biomed. Signal Proces. 2019, 50, 134–150. [Google Scholar] [CrossRef]
- Verotti, M.; Di Giamberardino, P.; Belfiore, N.P.; Giannini, O. A genetic algorithm-based method for the mechanical characterization of biosamples using a MEMS microgripper: Numerical simulations. J. Mech. Behav. Biomed. 2019, 96, 88–95. [Google Scholar] [CrossRef] [PubMed]
- Yeh, W.C. A squeezed artificial neural network for the symbolic network reliability functions of binary-state networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2822–2825. [Google Scholar] [CrossRef] [PubMed]
- Jethmalani, C.R.; Simon, S.P.; Sundareswaran, K.; Nayak, P.S.R.; Padhy, N.P. Auxiliary hybrid PSO-BPNN-based transmission system loss estimation in generation scheduling. IEEE Trans. Ind. Inform. 2016, 13, 1692–1703. [Google Scholar] [CrossRef]
- Liu, Q.; Brigham, K.; Rao, N.S. Estimation and fusion for tracking over long-haul links using artificial neural networks. IEEE Trans. Signal Inf. Process. Netw. 2017, 3, 760–770. [Google Scholar] [CrossRef]
- Hou, C.; Yu, X.; Cao, Y.; Lai, C.; Cao, Y. Prediction of synchronous closing time of permanent magnetic actuator for vacuum circuit breaker based on PSO-BP. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3321–3326. [Google Scholar] [CrossRef]
- Liu, C.; Ding, W.; Li, Z.; Yang, C. Prediction of high-speed grinding temperature of titanium matrix composites using BP neural network based on PSO algorithm. Int. J. Adv. Manuf. Technol. 2017, 89, 2277–2285. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Z.; Mei, Q.; Duan, J. Application of particle swarm optimization combined with response surface methodology to transverse flux permanent magnet motor optimization. IEEE Trans. Magn. 2017, 53, 1–7. [Google Scholar] [CrossRef]
- Ren, C.; An, N.; Wang, J.; Li, L.; Hu, B.; Shang, D. Optimal parameters selection for BP neural network based on particle swarm optimization: A case study of wind speed forecasting. Knowl. Based syst. 2014, 56, 226–239. [Google Scholar] [CrossRef]
- Mohamad, E.; Armaghani, D.; Momeni, E.; Yazdavar, A.; Ebrahimi, M. Rock strength estimation: A PSO-based BP approach. Neural Comput. Appl. 2018, 30, 1635–1646. [Google Scholar] [CrossRef]








| Parameters | Values |
|---|---|
| Swarm size | 10 |
| , | 1.49445 |
| Max iteration | 30 |
| 1 | |
| Number of the input layer nodes | 4 |
| Number of the hidden layer nodes | 10 |
| Number of the output layer nodes | 4 |
| Number of neural network training | 100 |
| Learning rate of neural network | 0.005 |
| Percentage of training data | 90% |
| Percentage of testing data | 10% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, D.; Chen, B.; Yu, L.; Qian, J.; Zi, B. A Clamping Force Estimation Method Based on a Joint Torque Disturbance Observer Using PSO-BPNN for Cable-Driven Surgical Robot End-Effectors. Sensors 2019, 19, 5291. https://doi.org/10.3390/s19235291
Wang Z, Wang D, Chen B, Yu L, Qian J, Zi B. A Clamping Force Estimation Method Based on a Joint Torque Disturbance Observer Using PSO-BPNN for Cable-Driven Surgical Robot End-Effectors. Sensors. 2019; 19(23):5291. https://doi.org/10.3390/s19235291
Chicago/Turabian StyleWang, Zhengyu, Daoming Wang, Bing Chen, Lingtao Yu, Jun Qian, and Bin Zi. 2019. "A Clamping Force Estimation Method Based on a Joint Torque Disturbance Observer Using PSO-BPNN for Cable-Driven Surgical Robot End-Effectors" Sensors 19, no. 23: 5291. https://doi.org/10.3390/s19235291
APA StyleWang, Z., Wang, D., Chen, B., Yu, L., Qian, J., & Zi, B. (2019). A Clamping Force Estimation Method Based on a Joint Torque Disturbance Observer Using PSO-BPNN for Cable-Driven Surgical Robot End-Effectors. Sensors, 19(23), 5291. https://doi.org/10.3390/s19235291





